义务教育阶段学生数学符号意识发展节点研究
—— 基于SOLO分类理论视角
2019-05-10朱立明武丽莎
朱立明,武丽莎
(1. 唐山师范学院 教育学院,河北 唐山 063000;2. 唐山师范学院 数学与信息科学系,河北 唐山 063000)
一、引言
(一)研究背景
《义务教育数学课程标准(2011年版)》(以下简称《标准(2011年版)》)中提出符号意识[1],标志着数学课程理念开始从以学科为本转向以学生为本。学生的数学学习过程中要不断同化数学符号及其关系。因此,在义务教育阶段数学课程中,学生除了要明白数学符号本身的意义,还应该更好地利用数学符号进行数学思考,这就要求学生具备一定的数学符号意识,因此,发展学生的数学符号意识既是数学课程目标,也是一种数学学科核心素养[2]。
(二)研究问题
数学符号意识作为义务教育阶段数学核心素养之一,具有内隐特征与外在表现[3],数学符号意识的内隐特征表现为以数学思维为内核的心理活动,外在表现是一种动态的数学符号能力,其外显性决定了学生数学符号意识的可测性。因此,本研究关键在于探寻义务教育阶段学生数学符号意识发展转折节点,为数学符号意识的培养提供指引。
二、理论基础
SOLO分类理论(Structure Of the Observed Learning Outcome)以结构主义为基础,旨在检测学生回答问题时所表现出来的思维结构,用来描述学生的反应及其层次水平,并将学生的学习结果划分为以下五种进阶式结构:(1)前结构水平:处在该层次水平的学生不具备解决问题的基础知识,或处于被无关知识困扰的混沌状态,不能获取问题解决的方法;(2)单一结构水平:处在该层次水平的学生过于关注题干中单一线索,并直接得出问题的答案;(3)多元结构水平:处在该层次水平的学生能够寻求更多相关性,但缺乏将其系统融合的能力;(4)关联结构水平:处在该层次水平的学生可以构建相关线索之间的联系,将其整合成为一个“线索群”,能够应对复杂问题的求解;(5)扩展抽象结构水平:处在该层次水平的学生会在理解、归纳的基础上将问题进行拓展,是更高层次的学习能力,表现出更强的创新意识与应用意识[4]。
三、研究方法与设计
(一)样本选取
本研究中学生样本的选取主要考虑以下两个条件:一是所选样本具有一定的代表性,二是所选样本具有测评研究的可行性。因此,考虑不同区域、不同水平的学校,在深圳、天津和长春共选取18所学校,其中小学、初中各9所学校,学校层次为优质学校、中等学校、一般学校三类,从三类学校1至9年级中各抽取一个普通年级,小学2 309人,中学1 168人,共回收有效测评问卷3 207份,其中小学2 039份,初中1 168份。
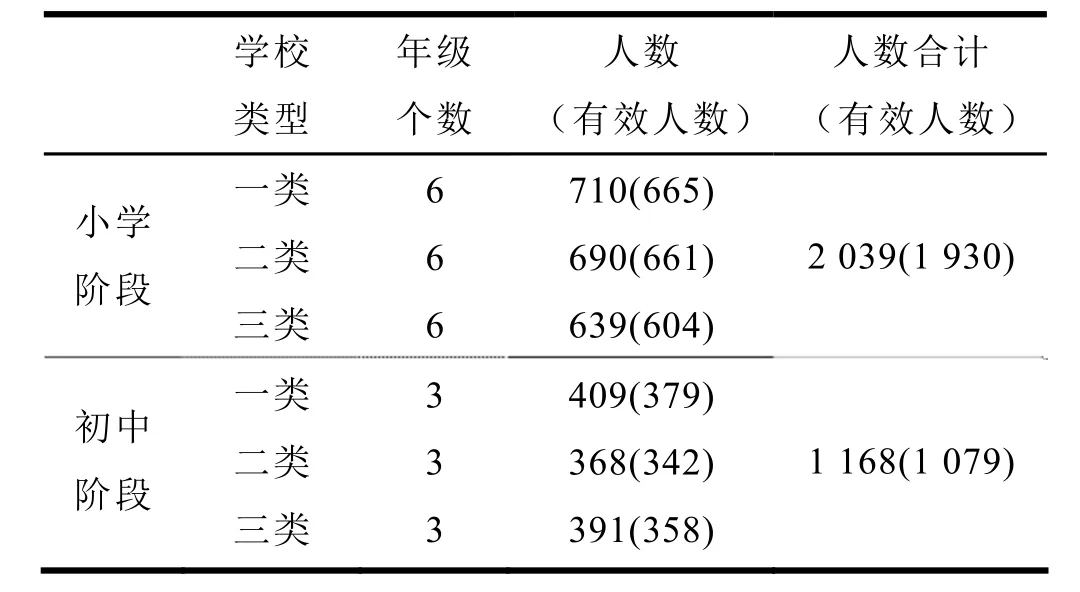
表1 学生调查样本分布状况
(二)工具设计
本研究通过词频分析,经过两轮专家咨询,最终构建了数学符号意识的四个分析层次,即数学符号的感知与识别(GS)①、数学符号的理解与运算(LY)、数学符号的联想与推理(LT)、数学符号的抽象与表达(CB)。
基于四个分析层次来设计题项,题项的选择主要考虑四个来源:(1)相关研究中的调查问卷;(2)《标准(2011年版)》中的典型问题;(3)对教科书中经典问题改编;(4)改造小升初以及中考试题。经多轮试测与修订后,调查问卷题项能够以《标准(2011年版)》作为基准,以现行教科书作为载体,以义务教育学段作为参考,以分析层次作为标尺,较好地控制了深度与广度。由于测评对象的年级跨度较大,涵盖了从1年级到9年级的学生,因此在问卷设计中,就需要考虑由于学生自身发展对测评带来的影响。为了更好地使问卷一致性与学生认知的发展性相统一,采用铆题消除由于学生的学习能力提升对学习内容所带来的影响[5]。经过检验,数学符号意识问卷各维度Cronbach’ Alpha值在0.807~0.828之间,总量表的Cronbach’ Alpha值是0.854,如表2所示。
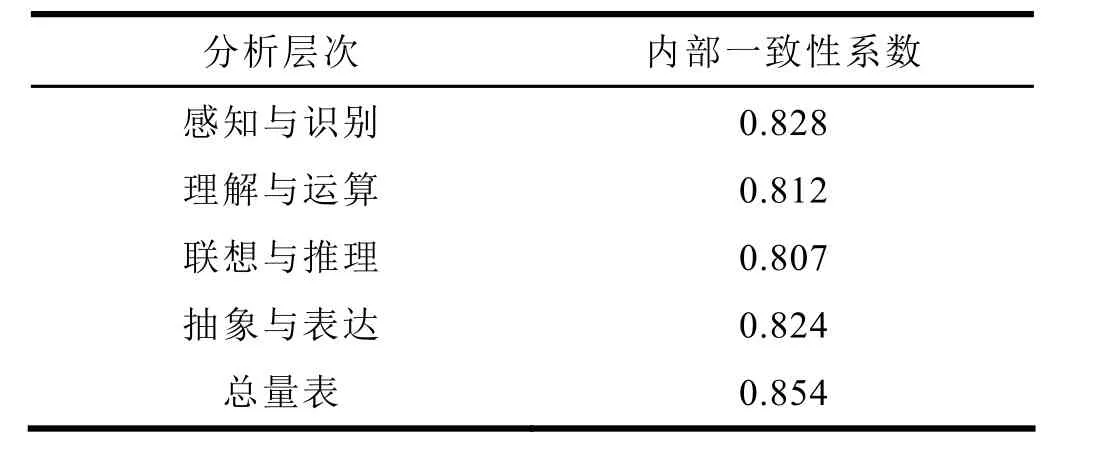
表2 各分析层次及总量表的信度状况
组内两两层次相关系数在0.154-0.645之间,为中、高程度正相关。四个层次与总量表之间相关系数在 0.568-0.880之间,表明各分析层次与整个问卷一致,达到高程度正相关。如表3所示。
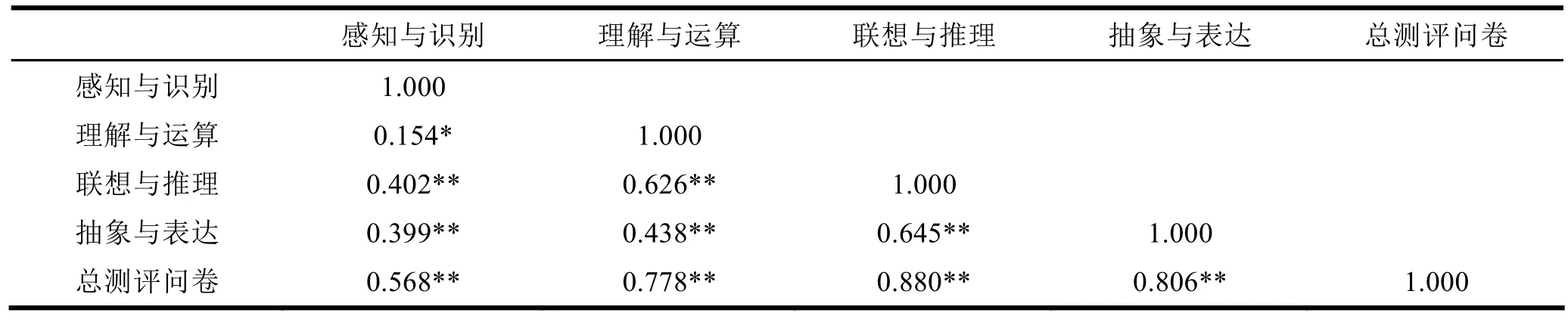
表3 各分析层次间的相关系数矩阵
(三)施测与评分
测评采用集中施测,要求学生在 40分钟内完成测评问卷,保证调查问卷的回收率与答题质量。在评分阶段,首先,初步制定详细的评分标准,与两名一线数学教师进行讨论,确定评分标准。其次,为了降低由一个评分者评分造成的测评误差,采用三人共同评分的方式,结果表明,评分一致性达到95%以上。
四、研究结果
(一)学生在数学符号感知与识别(GS)上的表现
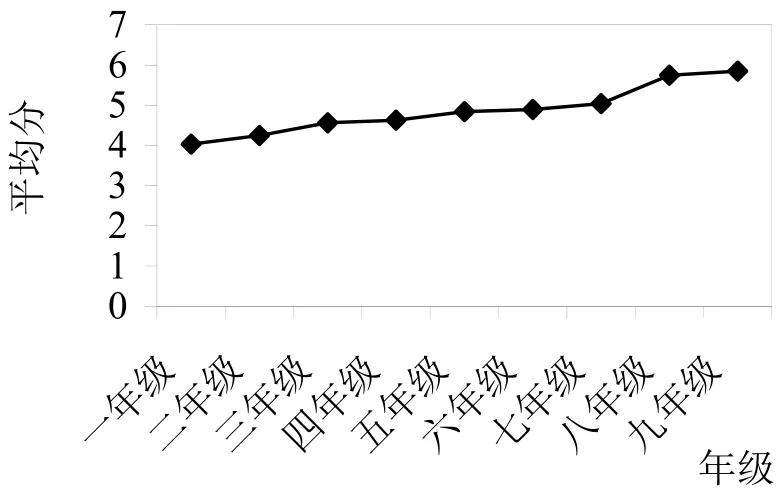
图1 各年级学生在数学符号意识GS层次平均分的变化趋势
研究结果表明,义务教育阶段学生在数学符号意识GS分析层次的平均分随着年级的增长逐渐升高,1年级到9年级的总平均分依次为4.035分,4.248分,4.563分,4.625分,4.841分,4.893分,5.038分,5.749分,5.851分。义务教育阶段学生的数学符号意识感知与识别层次的平均分均超过3.6分(每个层次总分为6分,视其60%为合格分,即为3.6分,下同),其中一年级学生的平均分最低,为4.035分,九年级学生的平均分最高,为5.851分。总体上义务教育阶段学生在数学符号意识GS分析层次上的平均分随着年级的增长稳定提升,具体如图1所示。
(二)节点一:二、三年级学生在数学符号理解与运算(LY)上的差异分析
从二年级到三年级是数学符号意识发展的第一次质变,如图1所示,两个年级学生在数学符号意识LY分析层次出现节点,二年级学生的平均分(M=2.706)低于 3.6分,而三年级学生平均分(M=3.674)高于 3.6分,这说明二年级学生没有达到数学符号意识的LY分析层次,而三年级学生达到了该层次,但三年级学生没有达到下一个层次(LT分析层次)。

图2 二、三年级学生在四个分析层次平均分变化趋势
对于二年级学生而言,大部分学生并不理解“⊕”运算的情境意义,而将其视为熟悉的加法或者乘法,并在题干8⊕5那里“纠正”为8+5=13。研究表明,学生不能通过运算法则来理解新定义的运算符号“⊕”②的意义,二年级学生所理解的“⊕”是基于生活经验的,更多是依赖于现实生活情境。运算应该在具体情境中进行理解,低年级学生往往借助形象化的事物来理解运算,例如加法运算就是把一些东西放在一起,计算它们的总数,对于结果的解释与算理的理解远远要比计算本身困难得多。也有一些学生能够根据运算情境,简单理解“⊕”的意义,对于有字母参与的运算则是束手无策;虽然三年级学生能够借助运算法则或运算情境来解读运算符号“⊕”的数学意义,也区分了“⊕”与加法之间异同,但总体上回答的也不尽人意。这至少说明,三年级学生能够建立新型运算与熟知运算之间的联系,将字母符号视为数字,把字母符号与数字联系起来,并尝试对其进行运算。

表4 二、三年级学生对测评题项的回答举例
(三)节点二:四、五年级学生在数学符号联想与推理上的差异分析
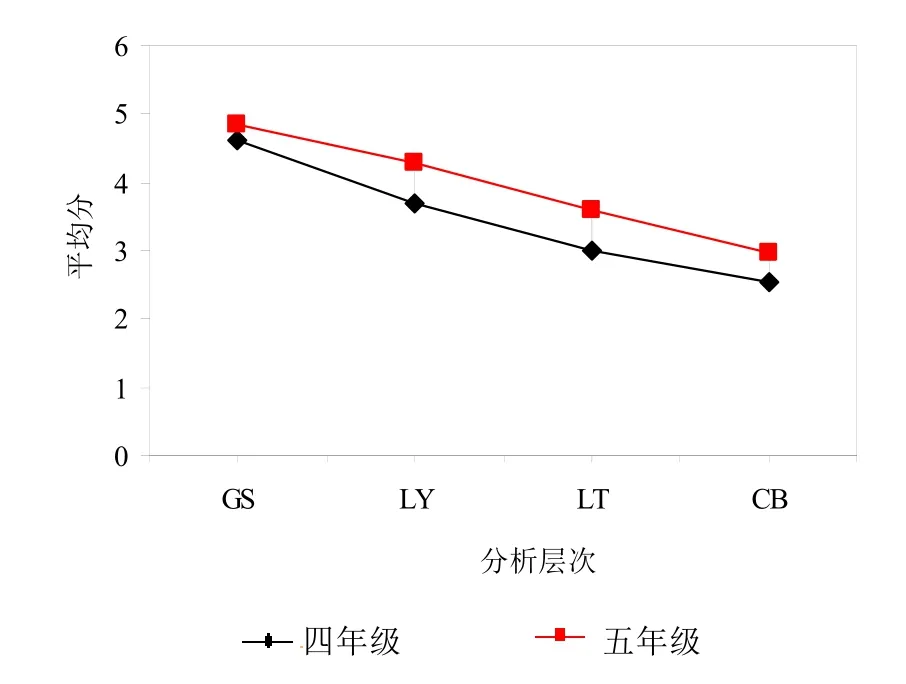
图3 四、五年级学生在四个分析层次平均分变化趋势
从四年级到五年级是数学符号意识发展第二次质变,两个年级学生在数学符号意识LT分析层次上出现节点,如图3所示,两个年级在数学符号意识LT分析层次存在差异,四年级学生的平均分(M=2.991)低于 3.6分,而五年级学生平均分(M=3.601)略高于 3.6分,这说明四年级学生没有达到数学符号意识LT分析层次,而五年级学生到达该层次,但五年级学生并未达到下一个层次(CB分析层次)。

表5 四、五年级学生对测评题项的回答举例
对于四年级学生而言,由于字母a的任意性,导致在比较“a+6”与“3a”的大小时,思维受阻,回答的结果也是混乱的,字母加入大小的比较给学生带来理解障碍。有些学生只是关注题目中的大小比较,急于给出“a+6”与“3a”的大小判断,所以,当想到一个特例或者某一个数字时,马上得出大小比较的结论。在同样的问题处理上,五年级学生的表现要远远比四年级学生灵活,学生已经清楚知道“a+6”与“3a”大小的非恒定性,其大小受到字母a的影响,因此,五年级学生能够探究字母 a是如何决定“a+6”与“3a”大小的,通过找到临界值,分情况加以讨论。由此可见,五年级学生已经能找到解决问题的通性通法,选取特殊值对问题进行解决,当特殊值找到后,还能联想特殊值与任意值之间的关联,利用归纳思维,由特殊值到一般规律,利用数学符号进行合情推理,使结论更具有一般性。
(四)节点三:七、八年级学生在数学符号抽象与表达上的差异分析
从七年级到八年级是数学符号意识发展的第三个质变,两个年级学生数学符号意识的 CB分析层次上出现第三个节点。如图4所示,七年级学生在 CB分析层次的平均分(M=3.125)低于 3.6分,而八年级学生在该层次的平均分(M=4.677)明显高于 3.6分,这说明七年级学生没有达到数学符号意识CB分析层次,八年级学生已经达到数学符号意识发展的最高层次(CB分析层次)。

图4 七、八年级学生在四个分析层次平均分变化趋势
对于七年级而言,学生能够理解题目要求,关注题目中的“两数之和为固定值”这一内容,在学生知识能力范围之内,找到了利用具体数字来解决问题的方法,大部分学生还是处在具体描述的层面,没有上升到抽象表达层面,学生只能利用文字来描述数量关系,不能从中抽象出数学符号,并利用符号进行表达。也有学生对这些数特征进行概括,如“用100分别减去100以内的数”“小数+大数=100”等,学生还是没有抽象出符号,并用数学符号进行数对关系的表达。仅少部分学生能够抽象出数学符号,利用数学符号来表达两个数之间的关系,使得表达结果具有一般性,整个抽象程度达到了最高。八年级学生能够发现满足条件的数对有无穷多个,也存在描述性回答,如“用100减去一个小于100的数”,大部分学生还是能够并从中抽象出数学符号(字母),利用数学符号表示一般性的结果,甚至有的学生已经明确给出字母的取值范围为任意实数,不仅能够将字母视为广义的数,还能够将其视为变量,利用字母表示了数对之间的抽象关系。

表6 七、八年级学生对测评题项的回答举例
五、研究结论
(一)义务教育阶段学生数学符号意识均达到感知与识别层次
数学符号的感知与识别是数学符号意识的第一个分析层次,也是其他层次的基础,主要描述的是义务教育阶段学生对数学符号与数字之间异同的认识。通过调查发现,一年级的学生能够掌握数学符号及其代表的数学意义与实际意义,能够感知并识别数学符号与数字之间的区别。学生能够明白可以用字母来表示不同的数字,但还不能理解字母表示数背后的意义及其数量关系。学生数学符号感知与识别随着年级的增长不断升高,在一年级时就能够很好地对数学符号进行识别,因此,这也在一定程度上表明,对于一年级学生,可以对其数学符号的感知与识别进行适当地培养,从而帮助学生初步感悟数学符号意识。
(二)处于节点的年级包含五种层次水平
根据SOLO分类理论,处于节点的年级表现出不同的水平,总的来说,包含了SOLO分类理论的五个结构水平,如表7所示,二年级与三年级学生的回答包含两种层次水平,三年级学生要比二年级学生的层次水平要高,但两个年级都没有达到扩展抽象结构水平。四年级学生的回答包含两种层次水平,五年级学生的回答包含三种层次水平,五年级学生要比四年级学生的层次水平要高。七年级学生的回答包含三种层次水平,八年级学生的回答包含四种层次水平,两个年级同时达到单一结构水平、多元结构水平与关联结构水平,八年级同时达到了扩展抽象结构水平。

表7 节点年级结构水平的分布情况
(三)处于节点的年级可划分三种进阶类型
义务教育阶段学生在数学符号理解与运算(LY)、联想与推理(LT)、抽象与表达(CB)三个层次出现节点,每个节点均包含由低到高的三种类型,第一个节点涵盖三种运算类型:算术运算型、形式模仿型、符号运算型;第二节点涵盖三种推理类型:猜想归纳性、特殊验证型、符号论证型;第三个节点涵盖三种表达类型:文字描述型、结构抽象型、符号表达型。
六、结语
数学符号意识的培养需要根据其发展阶段,帮助学生逐步强化建立数学符号意识,只有经历数学符号意识的进阶过程,学生才能从较低的数学符号意识发展水平过渡到高水平。而发展节点的研究,对于适时的数学抽象刺激或教学干预究竟能够带给学生数学符号意识发展的怎样的变化、每一个数学符号意识发展水平教学策略的遴选与实施均具有重要意义。义务教育阶段学生数学符号意识发展过程中不同层次的关键节点的探究,为义务教育阶段教师数学符号意识教学策略的选择奠定了理论基础。
[注释]
① 文中此处 GS为本研究对数学符号“感知与识别”的编码,取其汉语拼音首字母而成,下文LY、LT、CB其意相同。
② 文中“⊕”为本研究为测评学生对数学符号的理解与运算而新定义的运算符号,下文同此。
