南海东部海域A区块渗透率测井评价方法研究

聂世昌，刘心欣，刘财广，苏向群

(1. 长江大学 油气资源与勘探技术教育部重点实验室，湖北 武汉 430100； 2. 中国石油集团测井有限公司 华北分公司，河北 任丘 062552)

0 前 言

渗透率是认识储层特性、评价油气井产能、进行开发方案设计和调整工作的重要储层参数[1]。为了规避快速的勘探开发及日益复杂的勘探对象所带来的风险，进行油气储层渗透率的快速评价与预测则成为油气勘探开发关键的问题之一[2]。建立一套系统、快速而合理渗透率预测方案和技术能够对勘探的成果进行及时的检验、准确的预测有利目标区块、合理部署井位，适应快速的勘探开发节奏[3]。

对绝对渗透率计算方法的研究国内外众多学者做了大量工作，研究的思路可总结为：根据岩石物理实验数据，在分析影响绝对渗透率主控因素的基础上，建立绝对渗透率的统计模型；宋宁等[4]在分析KC模型的基础上，提出了基于划分流动单元的绝对渗透率算方法；Kozeny[5]基于毛管束理论，提出Kozeny绝对渗透率计算公式；还有通过岩石物理模型建立渗透率与储层特征参数之间的关系，Wyllie-Rose渗透率测井解释模型、Timur渗透率测井解释模型[6]等。

针对该区块储层类型多样，流体类型多样，对渗透率的计算较为困难的特点。

本课题拟采用针对能够反映储层类型以及流体类型的测井方法和技术对储层物性参数进行准确评价，比如利用基于流动单元理论的储层分类方法对渗透率进行预测以及利用能够反映储层流体信息的核磁共振测井信息来评价渗透率。

1 地质概况

研究区位于南海东部海域，自开展勘探以来成为中国近海重要的油气产区之一[7]。目前珠江口盆地已发现油气主要分布在几个已知的富烃洼陷内或周边，已发现大多数油气资源分布在珠江组及以上的中浅层。因此，一方面对于珠江口盆地成熟油气区而言，中浅层勘探程度相对较高，面临问题也很明确，构造圈闭规模越来越小，新领域、新层系油气勘探迫在眉睫；另一方面珠江口盆地(东部)有大面积的勘探新区，勘探潜力有待证实。研究区块珠江组储集空间以原生粒间孔为主，次生孔隙不发育。岩心物性分析资料表明，研究区的储层孔隙度范围为19.1%～26.4%，空气渗透率202×10-3～6 259×10-3μm2。

2 纯油气藏的渗透率

对于一定的均质流体来说,所测得的岩石渗透率称为绝对渗透率，用K表示。对同一岩心，K的大小与流体性质无关,仅取决于岩石的孔隙结构，对不同孔隙结构的岩心，K值是不同的。当有两种或两种以上的不能混合的流休(如油和水)通过岩心时，对其中某一种流体测得的渗透率称为有效渗透率。本文仅限于研究由孔隙结构决定大小的绝对渗透率,即研究单相流体在岩石孔隙空间流动时岩石导流的能力[8]。对低速、单相、稳定流，达西定律可由式(1)来描述：

(1)

式(1)中，Δp为流体压差；Q为在压差Δp下油的产量，m3/d；μ为油粘度，Pa·s；A为垂直于流体流动方向的截面积；K为绝对渗透率。

3 渗透率模型研究

分析渗透率与孔隙度、测井曲线的响应关系，优选与渗透率关系较好的的几条曲线[9]。根据渗透率与多条曲线的相关性，利用多元回归分析方法建立渗透率预测模型；可知渗透率与孔隙度曲线，自然伽马曲线响应较好(见图1～2)。

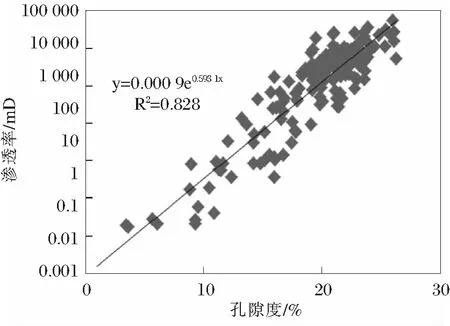
图1 渗透率与孔隙度的关系

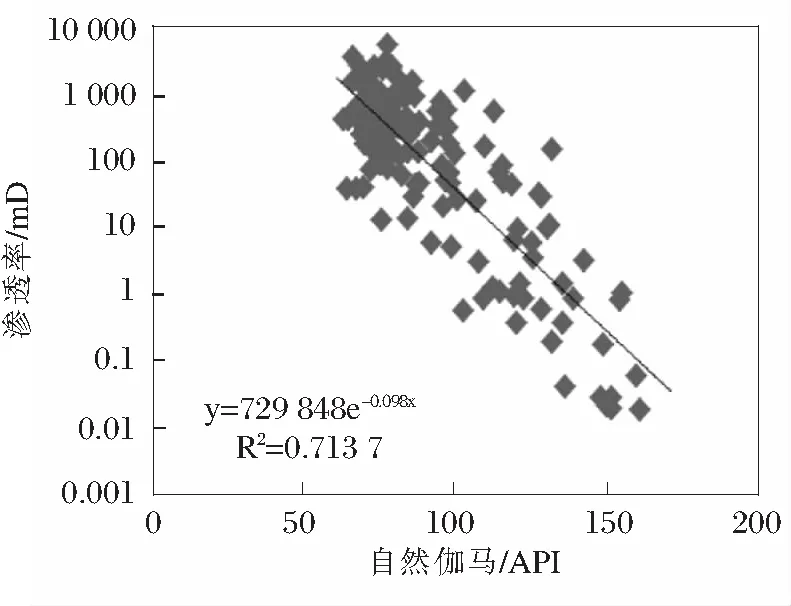
图2 渗透率与自然伽马的关系

由于渗透率与测井响应关系较为复杂，根据取心物性分析资料，采用流动单元划分储层的方法，对储层进行流动单元类别划分[10]，在流动单元储层类别划分的基础上，仍然采用交会图方法、有监督的模式识别方法等，建立储层类别划分方法或算法模型，达到利用常规测井资料对储层进行准确分类的目的，在储层分类的基础上建立每一类的渗透率评价模型来预测渗透率。由Kozeny-Carman方程得出的地层流动带指数与储层品质指数，可以表征如下。

储层品质指数(RQI)：

(2)

流动带指数(FZI)：

(3)

分类效果见图3～4。

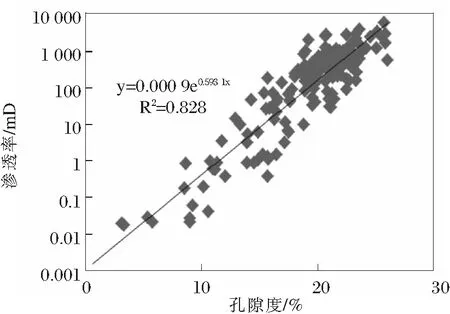
图3 渗透率与孔隙度的关系

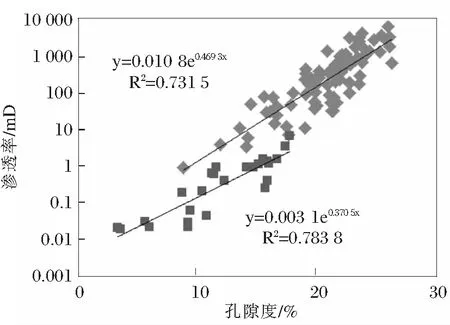
图4 渗透率与孔隙度分类之后的关系

利用核磁共振谱的计算方法就是从核磁共振测井的原始测量信息及机理出发，去推导横向弛豫时间谱与渗透率的理论关系。对于实际岩石来说，其孔隙网络由喉道和各种不同比表面积的孔隙所组成，理论公式中的比表面积应为岩石中所有不同比表面积孔隙的几何平均：

(4)

式(4)中，T2Distribution为横向弛豫时间分布(T2谱)，ms;(S/V)Distribution为岩石的孔隙比表面积集合平均值，m2/m3。

由式(4)可知，横向弛豫时间分布(T2谱)是对岩石中比表面积分布的综合响应，这也是核磁共振测井能够用以评价岩石的孔隙结构的原因。

Kozeny-Carman理论，有公式：

(5)

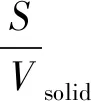
单位颗粒比表面积可由孔隙比表面积所表征，即有：

(6)

联立公式(5)与公式(6)，得到渗透率与孔隙比表面积的相关关系

(7)

而迂曲度 可由胶结指数与岩性系数表征，实验室中为了方便求取胶结指数常将岩性系数设置为1，对应的胶结指数为实际胶结指数，见式8：

(8)

式(8)中，m为胶结指数，无量纲；a为岩性系数，无量纲；m1为实际实验室条件下确定的胶结指数。联立式(4)、(7)、(8)，得：

(9)

通过对公式(8)分析可知：若对该方程进行一定的缩减，用某个参数代替T2分布，也可以进行核磁共振渗透率评价，但是对岩石微观特征刻画不细致导致其模型精度势必会受到影响。从信息论的角度来说，利用特征进行建模确实比使用所有数据进行建模精度要高，但是自由束缚流体体积比与T2LM并不是很好的特征，对于复杂的致密砂岩储层来说难以代表整个T2全谱。

4 渗透率模型应用效果分析

选取南海东部海域A区块19块代表性的岩样，对这19块岩样进行分析及核磁共振实验测量，分别获取了这19样的孔隙度，渗透率及核磁束缚水饱和度。分别用多元回归计算渗透率模型，流动单元计算渗透率模型，核磁 谱计算渗透率模型来计算19块岩样的渗透率，把计算的结果与岩心分析的渗透率进行对比(见图5)分析认为：3种模型中，核磁 谱计算渗透率模型要优于其他两种模型。

5 结 论

1)对渗透率的计算可优选与渗透率关系较好的多条曲线进行多元拟合；也可通过储层分类来进行渗透率的评价。

2)利用南海东部海域A区块19块岩心实验数据，分别获取3种渗透率模型中的固定参数，并利用已有的岩心数据对3种模型进行回判，结果核磁T2谱计算渗透率模型与岩心对比的结果优于多元拟合渗透率模型和基于流动单元划分的渗透率模型。

3)在有核磁资料的情况下优选核磁T2谱计算渗透率模型，核磁T2谱计算渗透率模型较为准确。

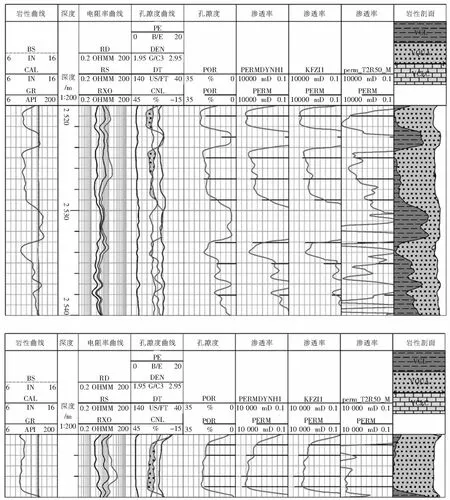
图5 3种渗透率模型的应用效果