加密云数据多级安全访问控制方案
2019-05-10张馨月严新成贾洪勇
张馨月,陈 越,严新成,贾洪勇
1(中国人民解放军信息工程大学 数据与目标工程学院,郑州 450001)2(郑州大学 软件与应用科技学院,郑州 450001)
1 引 言
随着云存储技术的迅猛发展,越来越多的企业和个人倾向于将应用软件和数据转移到云服务提供商的庞大网络数据中心存储,以减少自身管理和存储开销,方便数据共享.然而,当用户外包敏感数据到半可信的云存储环境时,会产生数据的机密性、完整性、可用性等问题,实现外包数据的安全访问控制是一重要研究的内容,各种技术手段陆续被提出[1].基于加密的方式实现访问控制可以以较小的代价实现最大的安全性.多级安全系统是指一类包含各种敏感等级信息,在不危及信息安全的情况下能够同时为不同安全等级的用户提供访问服务的系统,它是数据访问控制研究的一个重要方面,在军事和商业领域有广泛需求.经典的多级安全模型如Bell-La Padula(BLP)模型,其总体目标是防止高密级的信息泄漏给低密级的主体,以保护数据的机密性.许多属性基加密或者层次密钥管理方案通过数据加密或者密钥派生的方式实现敏感数据“禁止上读”特性,但是对数据“禁止下写”的研究还较为匮乏,作为BLP模型的一大特征,“禁止下写”特性保证了在机密性要求较高的系统中,高安全级的主体不能生成一个低安全级的密文数据,实现对其写权限的灵活控制.
本文针对在云存储环境下数据的多级安全访问控制问题,提出了一个层次密钥管理方案,数据拥有者可以实现其云端数据的多级安全访问控制,通过将读写密钥分开的方式,实现了BLP模型中“禁止上读”和“禁止下写”两大安全特性.并且高安全级用户可以通过密钥派生的方式计算出低安全级用户的读密钥,从而实现机密数据的安全共享.
2 相关工作
Akl和Taylor首先提出了等级密钥分配方案(Hierarchical Key Assignment Scheme,HKAS)[2],使得授权用户具有不同的数据访问权限,根据这些不同的权限,用户被划分至互不相交的安全级(Security Class,SC).通常情况下,HKAS具有一个中心权威机构,负责给每个安全级分配一些私有信息和加解密密钥,为了能够读较低安全级的数据,每个安全级可以由其私有信息和公开参数推导出当前安全级及其后继节点的解密密钥.HKAS可以应用于多种环境当中,例如云计算[3],无线传感器网络[4].
Akl和Taylor提出的第一个HKAS方案的缺点是计算开销随着安全级数目的增加呈指数级增长,且不便于访问权限动态更新.随后,许多改进的HKAS方案被陆续提出,它们或者具有更好的性能[5],或者支持动态改变安全级[6],或者更灵活的访问控制策略[7].2002年,W.Tzeng[8]提出了具有时间约束的HKAS,但是不能抵抗共谋攻击.有些HKAS方案基于椭圆曲线加密系统来解决访问控制问题[9-11],然而Das等[12]指出文献[9]中方案是不安全的:当一个新的安全级被插入多级访问结构时,外部攻击者可以通过寻根算法(Root Finding Algorithm)导出密钥;Lin和Hsu[11]指出Jeng-Wang的方案[10]会受到妥协攻击(Compromising Attack),即敌手可以从一个被删除的访问群组中获得当前访问结构中某些群组的密钥.文献[5]和文献[13]等方案均为间接访问,即不能直接派生出后继节点的密钥,需要迭代计算,开销较大.Tang等利用伪随机函数提出了一种密钥强不可区分安全的HKAS[14],Atallah等人提出了一个抵抗密钥恢复攻击的可证明安全HKAS[15],和一个密钥不可区分安全的HKAS[16].
Sahai和Waters提出了实现细粒度访问控制的属性基加密方案[17],只有属性集合满足访问控制条件的用户可以解密密文,文献[18]基于属性加密的方法实现了多级访问控制,但是各种属性基加密方案的访问控制策略只针对用户的读权限,对用户的写权限即加密数据的能力没有限制.
可以看出上述方案对BLP模型中写规则的研究还较为缺乏,文献[19]提出了一种基于代理重加密的HKAS,实现了满足BLP模型要求的用户读写权限灵活授权,但是需要迭代地计算低级别的用户私钥和重加密密文,计算开销较大.
3 预备知识
3.1 BLP模型
一个多级安全访问控制策略是一个五元组(SC,⪯,U,D,λ),其中SC={SCi:1≤i≤n}是安全级集合,表示所包含实体的敏感性;⪯是安全级间的二元关系,SCj⪯SCi代表SCi的安全级高于SCj的安全级,即SCj可由SCi支配,若既不存在SCi⪯SCj也不存在SCj⪯SCi,则安全级SCi与安全级SCj间不可比较,所以(SC,⪯)形成一个偏序集;U代表用户集合;D代表数据集合;λ:U∪D→SC是某一用户或者数据到某一特定安全级的映射.
如图1为一个多级安全访问控制策略示例,偏序集(SC,⪯)可由有向无环图G=(V,E)表示,图中的每个节点对应一个安全级,有向边(Vi,Vj)代表偏序关系SCj⪯SCi,Anc(Vi,G)表示节点Vi的所有祖先节点,Des(Vi,G)代表节点Vi的所有后继节点.策略图G可通过消除传递闭包属性中隐含的边来化简.
BLP模型是第一个将安全策略形式化的数学模型,为满足BLP模型的访问控制策略,P须满足如下两点:
1)简单安全特性:如果用户u∈U,数据d∈D满足λ(u)⪯λ(d),那么u不能对d执行读操作,即“禁止上读”.
2)*-特性:如果用户u∈U,数据d∈D满足λ(d)⪯λ(u),那么u不能对d执行写操作,即“禁止下写”.

图1 多级安全访问控制策略图Fig.1 Multi-level security access control policy diagram
3.2 双线性映射
G1和GT是两个素数p阶乘法循环群,g是G1的生成元,则称映射e:G1×G1→GT是双线性映射,如果e满足:
1)双线性:对于任意u,v∈G1,a,b∈Zp,都有e(ua,vb)=e(u,v)ab;
2)非退化性:e(g,g)≠1,1为群GT的单位元;
3)可计算性:对于任意u,v∈G1,e(u,v) 都是可计算的.
3.3 DBDH困难假设

|Pr[S(g,ga,gb,gc,T=e(g,g)abc)=1]-
Pr[S(g,ga,gb,gc,T=R)=1]|≤negl
4 CloudMLS方案
4.1 方案模型
如图2所示,在云计算环境下多级安全访问控制系统通常包含如下实体:中心权威机构、数据拥有者、用户和云存储服务器.中心权威机构负责用户注册和某些公开参数的生成,数据拥有者负责确定多级安全访问控制策略,将其数据按照不同的安全级加密后外包至云存储服务器中存储,并分配各安全级的读写密钥,用户根据自身安全级对云存储服务器中的数据执行读写操作.
本文提出一种基于线性几何的云存储层次密钥分配与数据加密方案CloudMLS,数据拥有者确定访问策略P可由有向图G=(V,E)表示,并计算一个公开矩阵来描述安全级间的支配关系,每个安全级对应着矩阵的一个行向量,并存在以下关系:
1)每个安全级的公开向量和私有向量是非正交的,内积为密钥生成参数,用于计算其读写密钥;
2)每个安全级的公开向量和其前驱节点的私有向量是非正交的,内积为一中间参数,用于计算前驱节点的读密钥;
3)其它情况,安全级的公开向量和私有向量内积为0.具体形式化描述见4.2节.
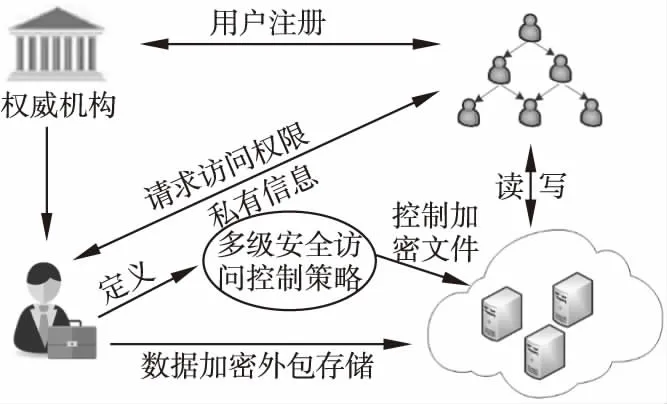
图2 多级安全访问控制模型Fig.2 Multi-level security access control model
在CloudMLS方案中,数据拥有者首先与权威中心交互获取系统公开参数,用对称密钥加密需要共享的数据,并将密文上传至云存储服务器,根据分配给每个安全级的写密钥加密消息(对称密钥)并上传.当用户加入时,首先在权威中心注册,确定安全级,与数据拥有者交互得到其私有信息,当欲执行读写操作时,某一节点的用户可以直接计算出其后继节点的读密钥,来解密低安全级的数据实现数据共享,但是不能计算出其前驱节点的读密钥,从而满足BLP模型中“禁止上读”的特性;由于用户没有后继节点用于生成写密钥的私有信息,无法计算出其写密钥,使得用户不能加密生成一个低安全级的合法密文,从而满足BLP模型中“禁止下写”的特性.
4.2 规则描述
在CloudMLS方案中,数据拥有者与权威中心交互获取系统公开参数,确定素数p阶循环群G1、GT,并为每个安全级SCi选定用于计算读写密钥(WriteKi,ReadKi)的参数ki,i,私有信息{(Yi,Zi),gi},其中Yi、Zi是两个二维向量,gi∈G1,为了处理不同安全级之间的支配关系,使得公开矩阵M可以表示访问策略P,针对各安全级的私有信息,我们利用线性几何中向量的正交性来确定如下3条规则:


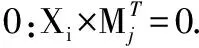
根据上述规则,我们给出用于安全级间读密钥派生的中间参数ki,j的定义:
(1)
矩阵K由所有ki,j组成.
用户u∈SCi根据其私有信息和公开信息可计算得到密钥对(WriteKi,ReadKi)及满足SCj⪯SCi的所有读密钥ReadKj,但无法得到其他安全级的写密钥,以此对用户的写权限加以限制,实现满足BLP模型“禁止上读”、“禁止下写”特性的安全数据共享,保护系统数据机密性.
4.3 具体构造
4.3.1SystemSetup(1δ,G)→(spi,pp)
根据安全参数δ和数据拥有者确定的多级安全访问结构图G,数据拥有者按照如下方式进行系统建立过程:
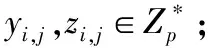
2)由私有信息Zi得到一个间接矩阵X:对于i=1,2,xi,1=zi,1、xi,2=zi,2,对于i≥3,xi,j=0;对于i=3,…,n,xi,1=zi,1、xi,i=zi,2,而对于j≠1且i≠j,xi,j=0,所以矩阵
计算间接矩阵X是否可逆,即|X|≠0是否成立.由于稀疏矩阵X的行列式可由|X|=(x1,1x2,2-x1,2x2,1)x3,3…xn,n求得,所以只须满足条件x1,1x2,2≠x1,2x2,1且xi.i≠0(i≥3) 即可.
3)数据拥有者为每个安全级SCi∈SC选取一个密钥生成参数ki,i,并按照如下方式并计算公开矩阵M:
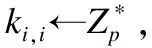
Step 2.根据上述规则1、2、3可得矩阵间关系X×M=K,由于X是可逆矩阵,于是可计算得到公开矩阵M=X-1×K.

4.3.2KeyGen(pp,spi)→(WriteKi,ReadKi)
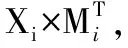
4.3.3Enc(WriteKi,m,pp)→(c1,c2)
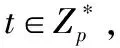
4.3.4KeyDer(SCi,SCj,pp)→ReadKi
密钥派生过程,如果安全级为SCj的用户想要获取安全级为SCi用户的共享数据,首先计算其读密钥,当且仅当SCi⪯SCj时,SCj可以通过其私有向量和公开信息获得SCi的读密钥,从而解密其密文.具体过程如下:

Step 2.若kj,i=0,则表示不满足关系SCi⪯SCj,即安全级SCi、SCj不可比较或者SCj比SCi安全级低,那么SCj无法计算出ki,i;否则,计算ki,i=yj,1kj,j+yj,2kj,i,ReadKi=gis·ki,i.
4.3.5Dec(ReadKi,(c1,c2))→m
解密过程,高安全级用户输入读密钥ReadKi和密文(c1,c2),计算m=c2/e(ReadKi,c1).
4.4 访问权限动态管理
4.4.1 增加一个新安全级
在当前访问策略中,对安全级SCi,SCj∈SC若有SCi⪯SCj,现欲插入一个新安全级SCt,使得存在关系SCi⪯SCt⪯SCj.
首先,数据拥有者随机选择私有信息((Yt,Zt),gt)及密钥生成参数kt,t,并通过安全信道发送给其中的用户.为保证方案的后向安全性,数据拥有者为所有比SCi低的安全级选择新的密钥生成参数ki,i,并按照系统建立过程计算公开矩阵M,涉及到的用户根据新的公开矩阵M和私有信息计算新的读写密钥对,重加密并更新其云端的密文数据.
4.4.2 删除一个安全级
当从当前多级安全访问结构中删除一个安全级,记为SCk,为保证方案的前向安全性,数据拥有者需要更新所有访问权限比SCk低的安全级的密钥生成参数,并根据新的多级安全访问策略图计算公开矩阵M,涉及到的相关用户计算新的读写密钥对.
4.4.3 多级安全访问结构中增加一条关系
若原多级安全访问结构中SCi和SCj不可比较,现在访问图G=(V,E)中增加一条Vj到Vi的路径,即增加了关系SCi⪯SCj,那么数据拥有者需要更新所有访问权限比SCi低和比SCj高的安全级的密钥生成参数,计算新的公开矩阵M,相关用户计算新的密钥对,更新其云端密文数据.
4.4.4 多级安全访问结构中删除一条关系
若安全级SCi、SCj对应的访问图G=(V,E)中的节点Vi、Vj存在Vj到Vi的路径,现欲删除关系SCi⪯SCj.那么需要更新安全级SCi及所有SCk的密钥生成参数,其中SCk对应的节点Vk满足Vk∈Des(Vi,G)且Vk∉Des(Vj,G),然后数据拥有者计算新的公开矩阵M,相关用户计算新的读写密钥对.
5 安全性及性能分析
5.1 BLP模型遵循性
本文提出的方案遵循BLP模型的简单安全性和*-特性.根据4.2规则描述中的规则1、2、3对多级安全访问策略P构建出公开矩阵M,使得安全级为SCi用户只可以利用自己的私有向量Zi和公开矩阵M计算出密钥生成参数ki,i,再利用公开参数计算出其读密钥,利用私有信息gi计算出写密钥;用户根据其私有向量Yi和计算出的中间参数ki,j可计算出低安全级SCj的密钥生成参数kj,j(对于不满足SCj⪯SCi的安全级SCj,会得到无效的间接参数ki,j=0,不能计算出正确的kj,j),由于没有私有信息gj,只能计算出SCj的读密钥,而不能计算出其写密钥,因此满足“不能上读”、“不能下写”的原则,遵循BLP模型的简单安全特性和*-特性.
5.2 抵抗合谋攻击
假设SCm的安全级高于SCm,1,…,SCm,h,h是一个正整数.如果这些低安全级的用户合谋,他们只能得到如下方程:
kmi,mi=km,mwm,1+km,miwm,2
=km,mwm,1+(xm,1ami,1+xm,mami,mi)wm,2
(2)
km,m=xm,1am,1+xm,mam,m
(3)
根据方程(2),合谋的恶意用户可得到:
(4)
其中,km,m、xm,1、xm,m、wm,1和wm,2对合谋的恶意用户是未知的.
令u1=km,mwm,1,u2=xm,1wm,2,u3=xm,mwm,2,则当h≥3时,可由方程组(4)计算得到u1、u2及u3的值,那么有:
(5)
由方程组(5)不能求得唯一的密钥生成参数km,m,所以即使低安全级的用户合谋也不能求得高安全级解密的读密钥,并且由于没有其他安全级的私有信息gi,也不能得到其用于加密的写密钥,所以本文提出的密钥分配方案能够抵抗合谋攻击.
5.3 数据机密性
为保证本方案数据机密性,证明对于某些非法用户,SCi*级的消息{m0,m1}中某一个加密的密文c*,判断出其到底是来自哪一个明文消息的概率Pr≤1/2+negl,其中negl是一个可忽略函数,{m0,m1}由非法用户选定.非法用户可以是非注册用户、已撤销用户或者注册用户,但是对于他们的安全级SCj,均满足SCi*⪯SCj.
定理1.如果DBDH问题是困难的,那么本文提出方案CloudHACS在选择明文攻击情况下是消息不可区分安全的(Message Indistinguishability,MI).
证明:如果概率多项式时间敌手A能以不可忽略的优势ε打破CloudHACS,那么可以利用敌手A构建一个算法Β来解决DBDH问题.算法Β输入五元组
因为私有向量(Yi,Zi)只用来计算当前及更低安全级的密钥生成参数,并只进行了代数运算,所以在模拟过程中,直接简化为对密钥生成参数ki,i的查询.算法B和敌手A的交互过程如下:
Setup:算法B输入DBDH元组
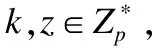
B返回相应的k和gi,并记录(SCi,gi,k,z,α);敌手A可按照如下方式得到读写密钥:ReadKi=((ga)z)k,WriteKi=(gi,(ga)k).其中SCi*⪯SCi;
Challenge Phase:敌手A选择两个等长的消息{m0,m1}发送给B,B计算gi*并得到元组(SCi*,gi*,k,z,α),B随机选择mt,t∈{0,1},返回c*=(gb,mt·Tzk)给敌手A;
Query Phase II:同查询阶段I;
Guess Phase:敌手A猜测密文c*对应的明文消息mt′,输出t′∈{0,1}.B验证下列条件是否成立:
i.安全级SCi*相应的α值为0;
ii.对于所有满足条件的A所查询SCi相应的αi=1.
如果B不满足任一条件,那么中止模拟过程;否则,若t′=t,则B输出1,其他情况则输出0.
如果B没有中止游戏,那么敌手A所得到的信息和真实的上述方案的攻击的情况一致.假设A在问询阶段I、II共做了q次查询,那么B没有中止游戏的概率为γq(1-γ).算法B输入DBDH元组,如果T=e(g,g)abc,那么挑战密文c*是安全级SCi*的消息mt正确形式加密的密文,敌手赢得游戏的优势为ε;如果T=R(R为GT中的随机元素),敌手赢得游戏的优势为0.所以,B有γq(1-γ)ε/2的优势解决DBDH问题.由于ε是不可忽略的,故而B以一个不可忽略的优势解决DBDH问题,这与DBDH假设矛盾,所以本方案是IND-CPA安全的.
表1 相关方案安全性对比
Table 1 Comparison for security

方案BLP模型遵循性安全性安全假设文献[13]×KIPRF文献[14]×KIPRF文献[19]√MIUni-directional PRE本文方案√MICPA-Secure+DBDH
本文方案和相关方案的安全性对比如表1所示,文献[13,14]均为密钥不可区分安全的(Key Indistinguishability,KI),本文提出的方案CloudMLS遵循BLP模型的同时是消息不可区分安全的.
5.4 性能分析
5.4.1 存储开销分析
安全级为SCi的用户需存储两对私有向量Yi=(yi,1,yi,2),Zi=(zi,1,zi,2)和私有参数gi∈G1,记群中元素大小为L,安全级的总数目为n,则每个用户需要大小为5L的存储开销.数据拥有者需要存储所有安全级的私有信息,需要5nL的存储开销.
5.4.2 计算开销分析
记m为平均每个安全级对应的低安全级数目,tF为函数F的计算开销,add、mul、inv和exp分别是群上的加法、乘法、求逆和模指数运算.
1)系统建立过程
数据拥有者计算中间参数ki,j需要2mn次乘法运算、mn次加法运算和n次求逆运算,计算公开矩阵M需要不超过3n2+2n+6次乘法运算、不超过3n2+2n+2次加法运算和n次求逆运算,所以系统建立过程数据拥有者的总计算开销为(3n2+(2m+2)n+6)tmul+(3n2+(m+2)n+2)tadd+2ntinv.
2)密钥派生过程
用户计算自身安全级的读写密钥共需进行2次乘法运算、1次加法运算和2次模指数运算,这一过程的计算开销为2tmul+tadd+2texp;用户计算某个低安全级的读密钥需进行4次乘法运算、2次加法运算和1次模指数运算,用户密钥派生总的计算开销为(4m+2)tmul+(2m+1)tadd+(m+1)texp.
3)加解密过程
加密过程需2次模指数运算,1次双线性运算和1次群乘法,一次加密计算开销为2texp+te+tmul,解密过程需要1次双线性运算、1次群乘法运算和一次群上求逆运算,一次解密的计算开销为te+tmul+tinv.
5.4.3 相关方案对比
本节中的使用符号含义如表2所示.本方案与文献[13,14,19]的存储和计算开销的对比如表3所示,可看出本方案中因增加了对用户写权限的限定,用户需存储的私有信息增加,但是密钥派生无须迭代的计算每一安全级的密钥,并且所需的群上的乘法和加法运算是非常轻量级的,降低了计算开销.
表2 符号含义
Table 2 Meaning of symbols

变 量含 义PRF伪随机函数SE-ENC对称加密运算SE-DEC对称解密运算Ψ.ReEnc代理重加密运算Ψ.Dec代理重加密中的解密运算Ψ.ReKeyGen重加密密钥生成运算#c(u)用户u可解密的密文数LVi安全级SCi和比其更低安全级的集合LEi与LVi中所有节点相关联的边miSCi安全级中的用户数量
表3 相关方案存储开销和计算开销对比
Table 3 Comparison of storage and computation overhead

方案用户存储开销密钥派生计算开销文献[13]L(d+1)tPRF文献[14]4L4tmul+2tadd文献[19]L2d·tΨ.ReEnc+2tΨ.Dec+tSE.DEC本文方案5L 4tmul+2tadd+texp
表4 用户撤销时的计算开销对比
Table 4 Computation overhead comparison of user revocation

方案密钥更新密文数据更新文献[14]O(|LVi|)#c(u)·tSE-ENC文献[19]O(|LVi|+|LEi|+mi)|Vi|·tΨ.ReKeyGen+2·#c(u)·tΨ.ReEnc本文方案O(|LVi|)#c(u)·(2texp+te+tmul)
当撤销SCi安全级的用户u时的密钥重分配的计算开销和密文数据更新开销对比如表4所示,其中文献[13]不支持用户访问权限动态变更,通过与文献[14,19]对比可以看出,我们的CloudMLS具有较高的密钥更新和密文数据更新效率.
6 结束语
本文针对云存储环境中多级安全访问控制问题提出了一种数据访问控制方案CloudMLS,该方案遵循BLP多级安全模型的“禁止上读”、“禁止下写”两大特性.利用线性几何中的向量内积来处理安全级间的关系,可以直接计算出低安全级的读密钥,无须迭代计算极大降低了计算开销,并通过将读写密钥分开的方式实现用户读写权限分别授权,然后针对该CloudMLS给出了用户权限动态管理算法,最后证明了方案在CPA模型下是消息不可区分安全的.
