基于低压电力线互联网通信中的一种新的均衡算法分析
2019-05-09张秀秀
张秀秀
(长治学院 电子信息与物理系,山西 长治 046011)
0 引言
现如今电力网的智能化发展迅速,在低压电力线上实现互联网通信成为可能。但是电力线作为通信信道,由于它的频率特性,噪声特性等导致在其上的互联网通信效果不佳。针对这些情况,在对电力信道充分分析总结的基础上,文章提出了一种适合电力线互联网通信的信道均衡新算法。
1 电力信道的特性分析
低压电力线上用电设备的随机接入和接出是影响电力线作为通信信道的不利条件之一,为了使得互联网通信在电力线上成为可能,通过对电网的实际观察与分析,总结出低压电力信道的特性。信道的时变性也很明显,信号在50 kHz~400 kHz范围内,衰减范围高达20多分贝。衰减随频率变化,但是对于互联网信号的间隔传输来说,电网信道仍然可以看成是慢时变信道[1]。因此,在电力信道桥接后,为提高通信的质量,在接收端加入自适应均衡器模块。下面将主要介绍适合于互联网通信新的变步长信道均衡算法[2]。
2 新的变步长均衡算法
本文是在文献[3]提出的舌线变步长DVS-LMS算法的基础上提出的一种改进式MDVS-LMS算法。
2.1 基于舌线的变步长LMS算法简介
该算法一开始运行时,μ(n)较大,在中间平稳阶段μ(n)会缓慢变小[3]。
DVS-LMS算法的迭代公式如下:
e(n)=d(n)-xT(n)w(n).
(1)
(2)
w(n+1)=w(n)+2μ(n)e(n)x(n).
(3)
式中,β决定步长μ(n)的界限,α决定步长曲线的形状。

图1 步长μ(n)与误差e(n)的函数曲线
从图1中可以看出,步长μ(n)与误差e(n)之间的函数关系。
2.2 改进的变步长算法
上面的算法在互联网通信中自适应均衡取得了较好的效果。然而,该算法会受到发送端不相关噪声的影响,这会导致算法在运行时的平稳度。针对文献算法存在的问题,本文提出了改进式MDVS-LMS算法,算法中用误差信号e(n)和e(n-1)来调整步长。新算法中还引入了补偿因子γ,其算法迭代公式如下:
(4)
(5)
其中,μmax=0.1,μmin=(0.005)。

图2 步长μ(n)与误差e(n)的函数关系曲线
从图2可以看出,通过对α、β、γ的适当选取,可以构造出符合变步长调整原则的曲线。新算法在低压电力线互联网通信系统中,对自适应过程中存在的误差信号e(n)在收敛阶段可能不相关的问题得以解决。
3 新算法的自适应均衡仿真分析
3.1 自适应均衡器的组成
为了比较新算法和文献[3]算法的性能优劣,文章中仿真实验采用具有一般性的恒参数信道。向量参数如下所示:
ISI_1=(0.05,-0.064,0.089,-0.125,
-0.25,0.9048,0.26,0,0.126,0.039)[4]
.
(6)
在比较两种算法的跟踪性能上,算法迭代一定的次数后,信道更换到2,信道2的向量参数如下所示:
ISI_2=(-0.24,0.904 9,0.039).
(7)
数据经过信道1处理后,再加上高斯白噪声一起进入自适应滤波器,实验中采用的是判决引导均衡器。均衡器为使得权向量系数接近最优,首先处于训练阶段,之后正式进入工作阶段。在此阶段采用判决检测器,由输出y(n)产生参考信号d(n),这时的误差信号e(n)为判决误差。
3.2 新的变步长MDVS-LMS算法仿真分析
两种算法在图3所示的环境中进行了仿真,发现信道特性都从迭代次数为2000后发生改变,针对DVS-LMS算法取不同的α,β进行了多次仿真,参数α=65,β=0.26时其收敛速度、均方误差的稳态值以及跟踪速度的性能最好。而新算法在α=65,β=0.35,γ=2时,性能最好。执行500次独立的模拟,然后进行平均计算,生成的均方误差曲线如图4所示。
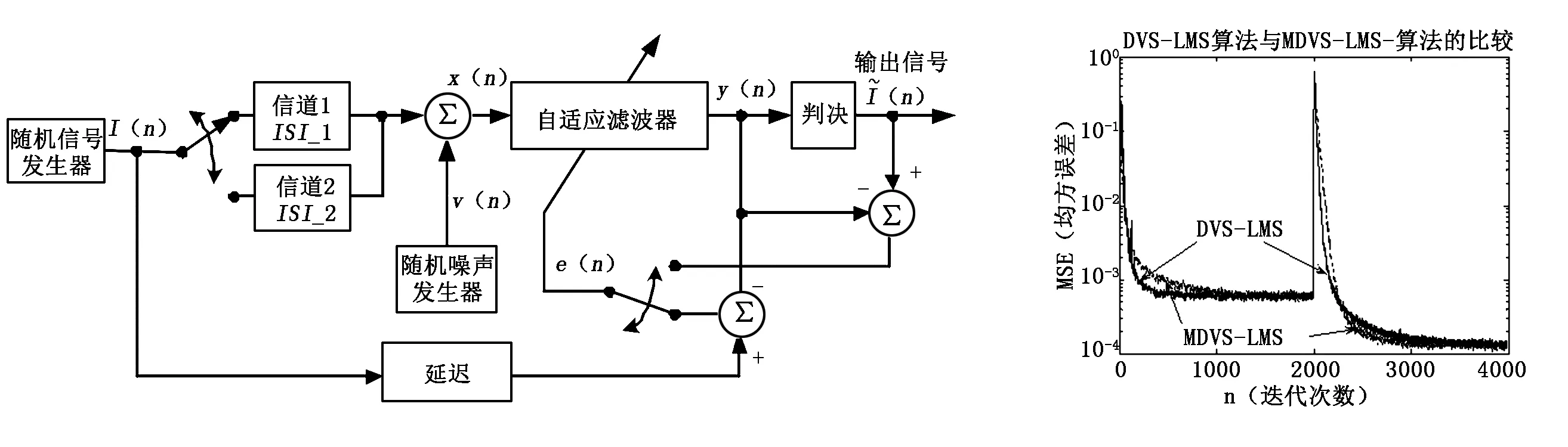
图4MDVS-LMS算法与DVS-LMS算法的均方误差比较图3自适应均衡实验框图
从仿真中可以看出,两种算法的收敛性都很好,相比文献提出的算法,本文改进的算法均方误差的稳态值更小一些,在信道特性改变后不但跟踪速度更快,而且均方误差的收敛速度也更快了。此算法适用到电力线互联网通信中,不需要先前自适应算法的指数运算。观察在2000点处信道发生改变时新的改进算法误码个数如图5所示。
从图中可以看出在2000点前,新算法的没有产生误码,在仿真信道更换到2时,算法进入跟踪阶段,在迭代次数小于40时,滤波器的系数重新收敛,之后表现出很好的跟踪特性,即没有产生新的误码。
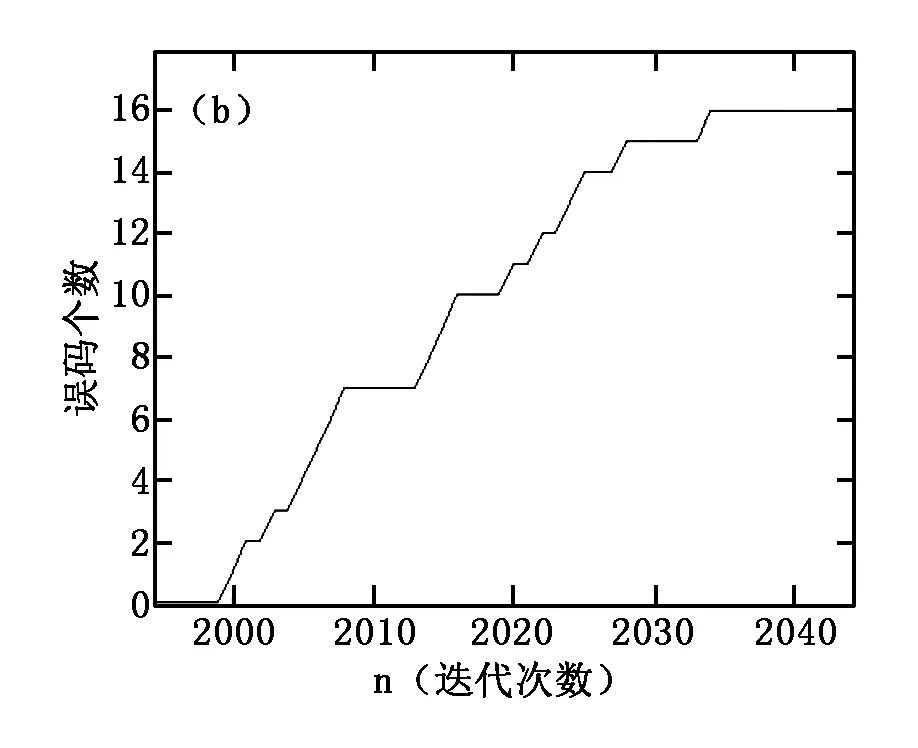
图5 MDVS-LMS算法误码个数
4 结论
本文提出的新算法在解决低压电力互联网通信过程中的信号衰减和码间干扰等问题有一定的改善。通过仿真发现改进的MDVS-LMS算法运算量小,收敛速度较快,跟踪速度也较快。总之,文章对改进算法的分析,对电网上实现较为可靠的互联网通信起到了一定的指导作用。
