纤维布加固混凝土方柱的改进约束强度模型

翟科杰，方圣恩,b

(福州大学 a.土木工程学院;b.土木工程防震减灾信息化国家地方联合工程研究中心,福州 350116)

既有工程结构由于设计、施工、材料质量等问题，以及新的荷载需求等原因，可能需要对结构进行加固。当前比较成熟的加固方法中，纤维增强复合材料法(Fiber Reinforced Polymer ，FRP)具有轻质高强、不增加构件截面尺寸等优越性能，在土木工程结构加固中得到广泛应用[1-4]。

素混凝土结构中无筋或不配受力钢筋，一般用于结构基础、重力坝、支墩、挡土墙等承力结构，对结构的整体安全性要求更高。目前，对FRP约束素混凝土柱的相关研究较多[5-6]，建立了各种约束混凝土强度计算模型。最初针对的是圆形截面柱[7-8]，此类柱在FRP环向约束后受力均匀，被约束混凝土的强度得到大幅提高。但现有建筑物中混凝土方形或矩形截面柱占绝大多数，受到FRP约束时，受力比圆截面柱复杂得多，特别是纤维布因在柱角部受力集中而可能早于其他部位发生破坏，使得约束作用大为降低。为此，加固时需将方柱四角进行倒角打磨处理，并对FRP约束区进行强弱约束区域进行划分[5]，然后在试验数据基础上结合理论推导，得到此类柱在FRP约束下的混凝土强度计算模型或公式。

值得注意的是，作为强度计算模型中最关键的参数，已有的各种强度计算模型在形状系数的选取上尚未统一，不利于加固设计和应用。同时，大多数强度计算模型仅局限于少量试验数据，有待进一步改进和完善。为此，本文根据试验柱的破坏模式，提出将方形柱强度计算模型中的有效约束区域和弱约束区域分割线重新定义为1/4圆弧，通过比较改进前后分割曲线在顶点处斜率变化率大小，统一了所选取约束强度模型的形状系数；然后，通过对比强度模型计算值与大量试验值之间的差异，评价改进后约束强度模型的准确性；最后，通过10根轴压素混凝土短柱试验，验证了改进模型对BFRP布加固柱的适用性。试验采用素混凝土柱，是为了避免配筋(特别是箍筋)对约束效果分析的影响。

1 混凝土约束强度模型

1.1 不同强度模型概述

FRP约束混凝土强度模型较多[9-13]，适用于FRP约束方形截面素混凝土柱的模型有以下几种。其中，式(1)、式(3)均相同，主要区别在于公式中的系数表达式(2)，特别是本文研究对象“形状系数”。

1)Lam & Teng模型[5]

(1)

(2)

(3)

(4)

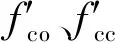
2)Al-Salloum模型[14]

(5)

(6)

文献中有效约束系数k1取为3.14，纤维布有效拉应变εf取为εFRP。

3)Ilki模型[15]

(7)

(8)

文献中k1=2.54，εf=0.85εFRP。

4)中国规范(GB 50367—2013)模型[16]

(9)

(10)

规范中k1=4，εf=0.003 5；Acor为被约束混凝土总面积。

5)ACI440.2R-08 模型[17]

(11)

(12)

规范中k1=3.3×ψf，其中ψf为折减系数，取为0.95；εf=0.55εFRP。

1.2 各强度模型区别

上述5种模型的核心计算式(1)、式(3)完全相同，均由FRP约束圆截面混凝土柱的强度计算模型演化而来，主要差别在于ks、k1、D、εf，其中，最关键参数为ks。

在k1的取值上，文献[5]模型基于试验取为3.3；美国规范[17]模型在文献[5]基础上考虑折减系数ψf，更为保守；文献[14]将k1取为文献[5]3.3和文献[18]2.98的均值；文献[15]根据试验结果取k1=2.54；中国规范[16]直接取k1=4。

在D的取值上，文献[5]与美国规范[17]均将矩形截面对角线看作等效圆直径；文献[14]为了使等效圆直径更加接近倒圆角后的真实值，在矩形截面对角线长度基础上减掉了倒圆角所减少的长度；文献[15]与中国规范[16]模型将D值取为被约束混凝土面积与矩形截面1/4周长的比值。

纤维布有效拉应变εf的取值在各强度模型中也不尽相同。文献[5]基于试验将εf定义为0.586倍的纤维布极限拉应变；美国规范[17]则取为0.55倍；文献[15]根据试验取为0.85倍；文献[14]则直接定义为极限拉应变；中国规范[16]中取值0.003 5，对一般构件取0.004 5。

在关键的形状系数ks取值上，5种模型均在二次抛物线分割的有效约束区与弱约束区基础上进行计算。文献[5]考虑到矩形截面长宽比对约束效应的影响，加入了系数(b/h)2，美国规范[17]对ks的取值参照了文献[5]；文献[14]考虑到约束力分布的不均匀性，加入了系数b/D；而文献[15]和中国规范[16]中的形状系数均未考虑截面形状及其他因素的影响。由此可见，各强度模型的ks差异较大。

总体上，各强度模型中的k1、εf是在试验基础上得到，D与柱截面尺寸相关，三者取值都相对客观。而ks的取值均基于二次抛物线分割，合理性值得探讨。同时，ks的表达式不同，也影响到实际工程应用时的便捷性。为此，先对ks进行了改进和统一，在保证约束混凝土强度计算精度的同时，工程应用上更加便捷。

2 改进约束强度模型

既有约束强度模型主要参照箍筋对混凝土的约束作用，将有效约束区域与弱约束区域采用4条二次抛物线分割开(图1)[5, 14]，抛物线两端点处切线与柱截面边长成45°角。而箍筋在混凝土中一般间隔分布，其约束效应与FRP存在明显区别。

图1 改进前模型有效约束区域[5, 14]Fig.1 Effective confinement areas before

本文结合文献[9]试验和文献[19]的模拟结果，针对有效约束区与弱约束区的分割曲线，提出采用4个1/4圆弧进行分割，同样地，圆弧在两端点切线方向与方柱截面边长成45°角，如图2所示。

图2 改进后模型有效约束区域Fig.2 Effective confinement areas after

图1中二次抛物线定义为

(13)

相应的一阶和二阶导数为

(14)

(15)

由此可得抛物线在A点处(图1)曲率半径：

(16)

而改进后A点(图2)曲率半径为

(17)

对比式(16)、式(17)可知，ρ2>ρ1，因此，改进模型曲线上A点及其临近弧线段的曲率小于改进前，与文献[19]中模拟结果(图3)及文献[9]试验结果(图4)更吻合，即有效约束区与弱约束区分界线在A点曲率很小(图3、图4中箭头指向处曲率)，可以认为，采用圆弧分割比二次抛物线分割更合理，因此，本文将有效约束区与弱约束区分割线定义为1/4圆弧。

图3 有效约束区与弱约束区模拟[19]Fig.3 The Figure of effective confinement area and weak confinement area based on simulation

图4 有效约束区与弱约束区试验图[9]Fig.4 The Figure of effective confinement area and weak confinement area based on

改进前，抛物线与正方形一边所围面积为

改进后，圆弧与正方形一边所围面积为

由于

因此，采用新的切割方法后，混凝土弱约束面积变小，而有效约束面积变大。

经过上述改进后，本文将1.1节中5种强度模型的形状系数统一表示为

(18)

该形状系数更方便工程设计和应用，且对文献[5]、文献[15]中国规范[16]及美国规范[17]中强度模型的影响较小，因为相对于方柱而言，改进模型的有效约束区域面积与原模型相差不大，且统一后的ks仍表示为有效约束面积与被约束混凝土总面积之比。但改进模型与文献[14]模型的形状系数相差较大，因为前者未考虑系数b/D，但这种差异可通过修正系数k1对模型进行校正。

改进ks后，利用文献[20]搜集的138条FRP约束方形截面混凝土柱试验数据即可直接评价文献[5]、美国规范[17]、中国规范[16]模型。此外，由于文献[14]中ks改进前后差异大，文献[15]模型基于中低强度混凝土试验数据建立，因此，本文修正了Al-Salloum和Ilki模型的k1，即根据文献[20]的试验数据，通过拟合的方式，取k1=2，同时，可以进行修正前后试验数据与理论计算的对比，若结果良好，则说明修正是正确的。

3 改进约束强度模型评价

文献[21]提出采用误差平方和∑Q评价约束强度模型的精确性。

(19)

式中:EXP和CAL分别表示试验值和计算值。可见∑Q越小，说明强度模型的误差越小，模型越精确。

根据文献[20]搜集的138条FRP约束方形截面混凝土柱试验数据(纤维布种类包括芳纶纤维、碳纤维、玻璃纤维)，对模型改进前后的强度模型进行评价，结果列于表1。由表1可见，改进模型的计算值更接近试验值(误差平方和∑Q降低)，特别是对文献[15]的Ilki模型而言，改进后的效果最明显，因为原模型只适用于中低强度混凝土，而改进后更适用于不同强度的混凝土，进一步说明了本文改进模型的必要性与合理性。值得一提的是，原Ilki模型计算值基本上大于试验值(图5)，偏不安全，不利于工程设计；而采用改进统一后的形状系数所得到的计算值，不仅更接近试验值，而且近一半试件的计算值小于试验值，偏安全。

表1 强度模型改进前后误差平方和Table 1 Error sum squares of strength models before and after improvement

图5 Ilki模型改进前后对比Fig.5 Comparison of Ilki model before and

4 试验验证

4.1 试验概况

工程加固中目前广泛使用的是碳纤维布，但其高价格也提高了施工成本。玄武岩纤维(Basalt Fiber Reinforced Polymer，BFRP)原材料为玄武岩，属于无机硅酸盐类，与混凝土组成材料水泥相同，二者相容性好。同时，玄武岩纤维绿色环保，耐久性、高温性能优于普通碳纤维，抗拉强度和弹性模量等材性参数也足够加固使用，更重要的是价格低很多，有利于工程推广应用。此外，文献[20]采用的138条数据未涉及BFRP约束加固的比较，有鉴于此，为了进一步验证改进模型对BFRP约束情况的适用性，进行了10根方形截面素混凝土柱轴心受压试验，其中，两根为未加固对比柱，8根为BFRP加固柱，后者倒角半径15 mm。5根方柱尺寸为150 mm×150 mm×300 mm,另5根为150 mm×150 mm×600 mm。实测混凝土立方体强度48 MPa，采用BFRP布全包裹方式加固，条布接头处搭接长度100 mm。BFRP布抗拉强度2 100 MPa，弹性模量105 GPa，厚度为0.107 mm。试件编号及加固情况列于表2。

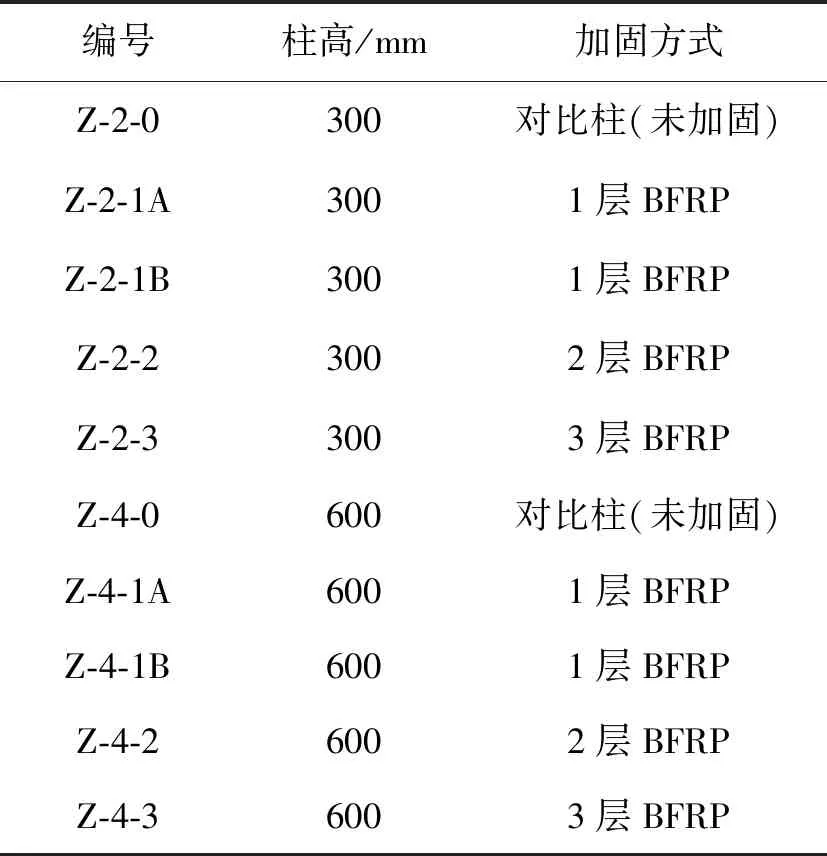
表2 试验混凝土柱Table 2 Experimental concrete columns

高度300 mm的柱试件试验在液压试验机上进行，采用0.2 MPa/s速率匀速缓慢加载；高度600 mm试件使用500 t油泵千斤顶加载(图6)，采用单调分级加载模式，每级15 kN，持载3 min，达到预估破坏值附近时，减小荷载步至5 kN。

图6 试件加载装置Fig.6 Loading devices for experimental

4.2 试件破坏现象

未加固对比柱：两根对比柱在加载前期均无明显破坏现象，直至柱身出现沿柱对角线方向的裂缝，然后突然破坏，破坏前无明显征兆，呈脆性破坏形态(图7)。

加固柱：所有加固柱破坏现象类似，在加载前期均无明显破坏现象。当外荷载增大至极限荷载附近时，纤维布发出噼啪断裂声，紧接着BFRP布突然爆裂，破坏前无明显征兆，呈脆性破坏形态(图6)。

破坏后试件关键截面照片如图8所示，可与图4进行对比。

图7 试件破坏情况Fig.7 Failure patterns of

图8 破坏后试件截面Fig.8 Specimen cross section after

4.3 试验结果分析

试验试件承载力实测及理论计算结果列于表3。鉴于中国规范模型[16]给出了构件承载力计算方法，本文承载力计算公式亦参考规范计算公式。

N=N0+Acor×4ksfl

(20)

式中：N0为未约束柱的承载力；ks为改进后形状系数。然后，将改进系数带入式(20)，并与10根柱的试验结果进行对比。

试验中，试件截面形状为边长等于150 mm的正方形(b=h=150 mm)，倒角半径r=10 mm。可计算得到改进前有效约束面积Sy=11 147.5 mm2，改进后Sy′=12 767.7 mm2，Sy

表3 改进模型与试验结果对比Table 3 Comparison between improved model and experiments

注：Z-2-1A加载过程中出现问题，故未得到试验承载力。

出于设计安全考虑，规范模型中对计算所得承载力乘了折减系数0.9，但本文出于试验验证的目的，考虑的是试件的极限承载力，因此，计算时暂不考虑折减。由表3可见，改进模型与试验结果吻合良好，说明改进强度模型对BFRP布约束素混凝土柱也具有良好的适用性和可靠性。

5 结论

对FRP布约束方形截面混凝土柱的有效约束区与弱约束区分割提出了新的定义方法，采用1/4圆弧分割替代传统的二次抛物线分割方法，通过结合既有数值模拟和试验试件的破坏形态，阐述了新分割方式的合理性。然后，进一步提出了约束混凝土形状系数的统一表达式，有利于工程实际应用。最后，基于文献[20]的138条试验数据和本文8根BFRP布包裹柱试验，验证了所提出改进约束强度模型对各种纤维布约束的适用性。通过理论和试验研究，得到以下结论：

1)本文8根FRP包裹柱试验结果表明，采用1/4圆弧替代二次抛物线划分受约束矩形截面混凝土更接近实际破坏情况，得到的有效约束区域更大。

2)总体上，在改进文献[5]、文献[14]、文献[15]、中国规范[16]、美国规范[17]中ks及文献[14]、文献[15]中k1后，约束强度模型精确度变得更高，对包裹柱的承载力估计更偏于安全。

3)利用既有大量试验和本文试验数据，验证了改进约束强度模型不仅适用于碳纤维、芳伦纤维和玻璃纤维，也适用于BFRP布约束。