NINO3.4指数的多模式集合预报方法

2019-05-09郭炜豪温文王晓春郑志海

热带气象学报 2019年2期

郭炜豪，温文，王晓春,郑志海

(1.南京信息工程大学海洋科学学院，江苏南京210044；2.国家气候中心/中国气象局气候研究开放实验室，北京100081)

1 引言

ENSO是厄尔尼诺 (El Niño)和南方涛动(Southern Oscillation)的合称，是热带太平洋表层海温年际变化最显著的信号。ENSO事件的发生可以造成包括我国在内的世界许多区域的气候异常，引起降水、气温、反气旋等的相应变化[1-3]，因此，ENSO季节预报有极大的社会应用价值。

集合预报在1969年首先由Epstein[4]从大气运动的随机角度提出。后来，Leith[5]在1974年提出了一个比较适合于实际应用的“蒙特卡罗”预报方法。单一模式的集合预报可以有效降低预报中的误差，并定量估计预报的不确定性，但由于不同模式间的预报结果有着明显的差异，为减少各个模式预报的不确定性，多模式集合预报方法得到了发展。Fraedrich等[6]通过线性回归方法把两个统计预报方案进行组合试验，并将该方法应用于热带太平洋月平均海表温度的长期预报。在Krishnamurti等[7]的超级集合预报中，利用训练期中模式的预报效果估计不同模式的权重以及模式预报与观测之间的回归系数。智协飞等[8]利用滑动训练期及多种多模式超级集合的预报方法进行了广泛试验，进一步提高了预报效果。在此基础上，大量的研究表明，等权平均的集合预报一般优于单个模式的预报，而采用不同权重进行加权平均有助于进一步提高集合预报效果[9-11]。

贝叶斯模式平均方法 (Bayesian Model Averaging，BMA)基于训练期内单个模式产生最好预报的条件概率来估计模式权重。BMA可发布概率形式的预报[12]，也可用于发布确定性预报[13-14]，自这一方法由Raftery等[15]提出以来，已在集合预报领域得到了大量应用。Wang等[16]基于BMA发展了多个模式的客观权重集合预报，对中大西洋海湾的海表温度进行预报并与单一模式预报和集合平均预报的预报精度进行比较，结果表明，客观权重集合预报要优于单一模式预报和集合平均预报。智协飞等[17]利用CMIP5多模式输出结果对气温的预报也有类似的结论，并指出训练期的长短会影响BMA中参数的估计，对BMA预报结果产生影响。

尽管ENSO事件是季节尺度气候变化最显著的信号，但其季节预报仍有很大的不确定性，比如美国哥伦比亚大学国际气候与社会研究所(International Research Institute for Climate and Society，IRI)每月依据全球多个预报机构的季节预报来发布ENSO预报，但只提供了等权的多模式集合预报，并没有考虑单个模式在过去一段时间内的预报效果。本文利用IRI发布的季节预报，选择了2002年2月—2015年10月7个模式的预报结果，利用BMA构造了NINO3.4指数的客观权重集合预报(OBJ)，期望能提高预报精度，为ENSO事件的发生提供更加可靠的预报。

2 资料

美国哥伦比亚大学国际气候与社会研究所每月都提供多模式实时ENSO预报[18]，目前包括的模式有10余个，基于提供NINO3.4指数预报的连续性考虑，为发展本文的客观权重集合预报，我们选择了7个单一模式，这7个模式2002年2月—2015年10月提供NINO3.4指数未来9个月的滑动平均预报值。表1是本文所用到的7个单一模式基本情况的介绍，除Scripps Hybrid Coupled Model(HCM)是动力-统计相结合的模式外，其它都是统计模式。Zheng等[19]利用这些模式的输出结果分析了ENSO中可预报的部分。关于IRI中ENSO模式预报的详情，可以参见Barnston等[20]。

表1 本文所用到的NINO3.4预报模式的名称和简单介绍

为在训练期内确定多模式集合预报的参数及评价预报效果，我们利用扩展重建海表面温度资料[21]计算了2002年1月—2016年6月逐月NINO 3.4指数。此外，由于不同的资料之间存在一定的不确定性，本文采用了美国国家海洋和大气管理局(NOAA)的全球月平均再分析资料(OISST)[22]进行验证(图略)，结果表明，两者计算得出的NINO 3.4指数高度一致，为了便于讨论，本文在后续讨论中均使用ERSSTv4的计算结果作为NINO3.4指数的“真值”。国内也有相应的研究成果[23-26]。

3 多模式集合预报方法

3.1 集合平均预报

对某一预报量y,比如NINO3.4指数，当有K个模式可以提供这一预报量的预报时，这些预报的算术平均为，

往往可以提供更加准确的预报。在上式中fk(k=1,……，K)为K个单个模式的预报。这种方法计算简单，可以有效地提高预报精度，在多模式集合预报中得到广泛应用。但这种方法所有的模式使用一样的权重，不能有效地提高集合预报的预报效果。

3.2 客观权重集合预报

基于贝叶斯模式平均方法 (Bayesian Model Averaging)[20]，在fk为 y最好预报的条件下，y的条件概率密度函数为g（y|fk），按照全概率公式，

其中的wk是模式k的预报为最好预报的概率。wk可以依据训练期内 K个模式的预报和 y的观测值来确定。因为wk是概率，所以wk大于零，并且wk(k=1,……，K)的和为1。进一步假定条件概率g(y|fk)满足期望值为ak+bkfk，方差为σ2的正态分布，则y的期望值为，

参数wk(k=1,……,K)可以根据一段时间内 K个单个模式预报及观测值用最大似然法来估计[15,17]。

由上式也可以看出，集合平均预报，

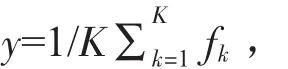
为客观权重集合预报的特例。当 wk≡1/K，ak≡0，bk≡1时，客观权重集合预报则退化为集合平均预报。利用ak，bk这两个参数，客观权重集合预报可以有效地订正单个模式的系统性偏差，wk反映了训练期内单个模式预报对集合预报的相对贡献。本文中，我们使用NINO3.4指数2002年2月—2015年10月的观测值、7个模式的预报值来估计参数 wk、ak、bk(k=1，……，K)。

对于不同的超前月份，客观权重集合预报可以估计不同模式的权重wk，图1中，色条的长度表示模式的权重大小。从图中可以看出，不同的超前时间，预报模式的权重分布也不同，如Scripps动力-统计相结合的耦合模式(HCM)在超前两个月的预报中由于预报精度低于其他模式，因此权重较小；而在超前8个月的预报中，由于模式预报结果更接近观测值，因此权重增大。在客观权重集合预报方法中，单个模式的权重可以依预报超前月份而变化，模式预报技巧随超前月份的变化可以考虑在客观权重集合预报方法中。

图1 各单一模式权重随预报超前月份的变化

4 预报结果比较

4.1 非独立样本的预报试验

本文首先将2002年2月—2015年10月 (共165个月)作为估计客观权重集合预报参数的训练期，得出各个模式的参数后，对2002年2月—2016年6月的NINO3.4指数进行客观权重集合预报。图2为7个单一模式预报、集合平均预报和客观权重集合预报的结果，其中虚线是单个模式预报，蓝色线为集合平均预报，红色线为客观权重集合预报，黑色线为利用ERSSTv4计算的NINO3.4指数。为清晰起见，图中只画出以每年1月观测值作为起点，对2—10月进行的预报。

图2 单个模式、集合平均预报和客观权重集合预报对NINO3.4指数超前9个月的预报

图2 表明，与单个模式的预报相比，集合平均预报和客观权重集合预报可以明显地提高预报技巧。比如，对于从2011年1月开始的预报，部分单一模式的预报与实际观测差别很大，而客观权重集合预报和集合平均预报的结果更加接近实际情况。另外可以看出，尽管集合预报有效地提高了预报的精度，但在某些极端事件中，如2015—2016年的El Niño事件，单个模式预报以及两种集合预报的预报精度仍有待提高。

对预报时效为1～9个月的预报，随着预报时效的增加，NINO3.4指数的预报误差也逐渐增加，但对于不同的预报时效，客观权重集合预报的均方根误差要比集合平均预报小(图3)。

单一模式预报、集合平均预报和客观权重集合预报的预报结果表明，集合平均预报比单一模式的预报精度高，而客观权重集合预报的预报精度要高于单一模式和集合平均预报(图4)。平均来说，客观权重集合预报比集合平均预报模式的预报精度提高了4%，与单一模式预报相比，集合平均预报的预报精度提高了2%～29%，客观权重集合预报的预报精度提高了6%～34%。

图3 集合平均预报和客观权重集合预报在不同超前月份的均方根误差的比较

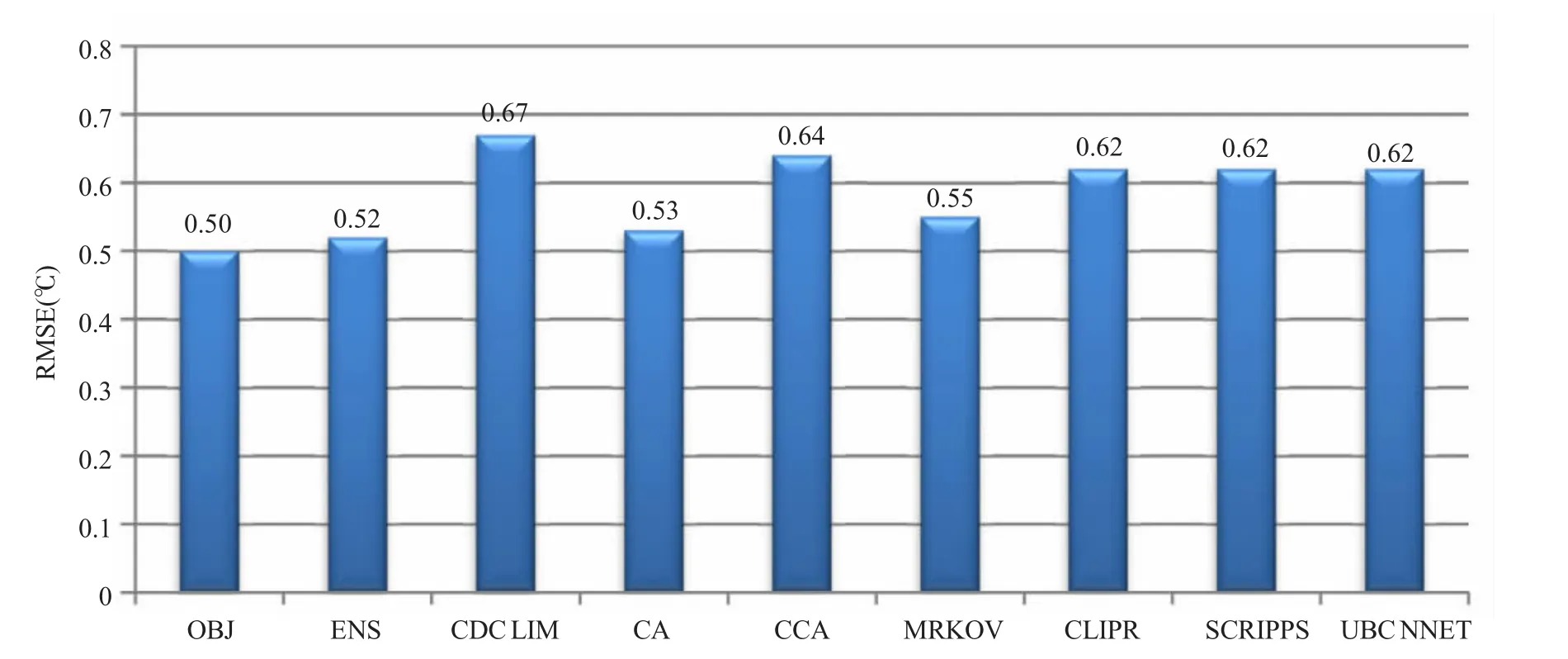
图4 单一模式预报、集合平均预报和客观权重集合预报超前1～9个月的均方根误差的比较

4.2 独立样本的预报试验

以上比较使用了2002年2月—2015年10月的所有数据，即估计客观权重集合预报参数及预报结果验证使用了同一组数据，两者不是独立的。我们为进一步评价客观权重集合预报的预报效果，进行了独立样本的预报试验，即将2002年2月—2015年10月共165个月的数据分成两组，一组用来估计客观权重集合预报方法的参数(即训练期)，另一组用来评价预报结果(即预报期)。训练期的长度从84个月开始逐渐增加，用其余的数据进行9个月的预报，并比较客观权重集合预报与集合平均预报与观测的均方根误差(RMSE)(图5，见下页)，图5中横坐标为训练期长度，纵坐标为RMSE。结果表明，在绝大多数的情况下，客观权重集合预报的预报效果更优，其均方根误差比集合平均预报降低了4%～17%。在个别情况下，比如训练期为90个月及102个月时，集合平均预报的均方根误差要低于客观权重集合预报。表明训练期的长度将影响客观权重集合预报的参数估计及精度。