基于多普勒天气雷达的低空多普勒速度的切变识别算法研究

闫文辉，黄兴友，李盈盈，杨敏，刘燕斐

(南京信息工程大学气象灾害预报预警与评估协同创新中心，江苏南京210044)

1 引 言

低空风切变是指600 m高度以下空间两点风的矢量差，即风向、风速在空间两点突然大幅度变化的一种现象[1]。低空风切变是威胁航空安全的重要原因之一，特别是在飞机起飞和降落阶段，由于飞机在低层大气遭遇风切变之后，空速、升力骤变，导致飞机失速和操纵困难，甚至会发生坠机。国际民航组织2005年进行的一项调查显示，1964—1983年，低空风切变至少造成了全球28次大型民航飞机事故，500多人死亡，200人受伤[2]。2015年2月台湾复兴航空公司的飞机在机场降落过程中，遭遇低空风切变，导致机上乘客与机组人员48人死亡，10人受伤[3]。因此，研究出快速可靠的低空风切变识别预警算法，是降低飞行风险的一个有效措施。

在低空风切变识别方面，国内外开展了一系列研究。Wilson等[4]利用多普勒雷达数据分析了微下击暴流风场的水平和垂直结构，并提出利用多普勒雷达进行微下击暴流识别和低空风切变灾害预警的可能性。Uyeda等[5]第一次开发了一种基于径向速度梯度的阵风锋识别算法，Campbell等[6]研制了一种基于人工智能的低空风切变自动识别方法。Evans等[7]描述了集成的业务化风切变预警系统，该系统一般由激光雷达风切变预警系统(LIWAS)和终端多普勒天气雷达系统(TDWRS)构成，已在美国几十个机场实施，效果明显，香港机场也采用了类似的低空风切变预警系统。此外，Boilley等[8]利用高分辨率的数值模式对Nice-Cote d'Azur机场的低空风切变进行预报。Augros等[9]将多普勒雷达径向风速投影到笛卡尔坐标系中，对比邻近格点风速的差别来识别风切变。

国内学者对风切变的识别和预警也进行了不少研究，段鹤等[10]详细介绍了典型飑线发生时多普勒速度回波特征及风切变的位置。王珊珊[11]基于直接计算差值滤波算法识别了低空风切变，并以动态链接库的方式实现了工程设计。王楠等[12]采用最小二乘法识别了低空风切变和辐合线，并讨论了拟合“窗口”大小(即参与计算的资料点数n)对资料预处理效果和梯度计算的影响。魏耀等[13]提出了拟合“窗口”随探测距离远近而变的最小二乘法低空风切变识别算法，发现其优于直接计算差值滤波算法。胡琦[14]利用香港国际机场多普勒激光雷达数据，使用灰色预测、BP神经网络等4种算法，得到了预测风速图，并用于低空风切变的预警。Wang等[15]基于区域增长算法识别了不同高度水平风的水平和垂直切变。周生辉等[16]利用VVP风场反演的方法进行了低空风切变识别分析。蒋立辉等[17]针对新一代多普勒天气雷达单尺度的风切变识别方法容易产生漏报的问题，提出了基于自适应多尺度的梯度搜索风切变预警算法。杜爱军[18]采用最小二乘法和退模糊技术，计算了基于南京信息工程大学C波段双偏振雷达资料的二维合成风切变。国内还有较多相应的研究[19-23]。

低空风切变是在不同的天气背景和环境条件下形成的，因而具有不同的空间(水平)尺度。但国内的低空风切变识别算法都是通过单一尺度的一维径向风切变、一维切向风切变和二维合成风切变来判别低空风切变的位置、强度。这些算法不能很好地识别各种尺度的低空风切变，容易产生漏报现象。而且拟合“窗口”大小的选取带有人为主观性，会影响低空风切变识别结果。此外，一维径向切变值随着拟合“窗口”的增大而减小，因为窗口越大，平均作用越强。拟合“窗口”过小，计算结果会受到预处理后残留噪声的影响；拟合“窗口”过大，可能会将某些大切变区漏掉。本文的自适应多尺度低空风切变识别算法，可有效解决“窗口”大小的问题。

本文对已有风切变识别算法中存在的单一尺度问题进行了分析，根据风切变强度因子，自适应选择合适大小的拟合“窗口”，采用最小二乘法，自动处理二维合成风切变。并与我国新一代S波段多普勒天气雷达(CINRAD/SA)的二维合成风切变产品进行了对比分析。此外，本文还计算了垂直风切变和时间风切变，实现了低空风切变的四维识别预警，为飞行安全提供保障。

2 低空风切变识别算法

2.1 自适应拟合“窗口”选取

风切变强度因子是Woodfield等[24]提出的，它是衡量低空风切变强度的有效标准之一，其计算公式如下：

式中dv/dt是风速变化率(沿着拟合路径)，Δv是风速变化量(沿着拟合路径)，Vapp是飞机的正常进近速度，H表示拟合路径尺度。最大风切变强度因子所在的局部区域一般最容易发生低空风切变。

根据飞机的响应时间，风切变强度因子的计算“窗口”分别选为0.5 km、1 km、2 km和4 km四个尺度。在同一距离库处，沿径向分别计算四个尺度下的风切变强度因子值。比较四个风切变强度因子值，取最大因子值所对应的尺度作为该距离库一维径向风切变计算的自适应拟合“窗口”。以此得到每个距离库的一维径向低空风切变计算的自适应拟合尺度。同理，在同一探测距离上、得到距离库的一维切向低空风切变计算的自适应拟合窗口尺度。

2.2 基于最小二乘法的二维合成风切变算法

2.2.1 一维径向风切变

对于一维径向风切变(RS)，自适应拟合“窗口”包含n个距离库，即：

式中vi是“窗口”中第i个距离库的径向速度，ri是相应点与雷达之间的径向距离，利用最小二乘法计算一维径向风切变的方法如下。

设线性回归方程为：

式中v*是拟合“窗口”速度估计值，a为初始值，b为斜率，r是径向距离。

则估计值与实测值之间的误差为：

根据最小二乘法原理，使上述误差平方的和最小，即使下式取最小值。

分别对a、b求偏导并令其等于0，即：

解式(6)得：

如图1所示，A点和D点之间的一维径向风切变是(vD-vA)与资料点总长度ΔR之比。而按照式(5)，斜率b是(vD-vA)与A、D两点之间的距离Δr的比值。则一维径向风切变的大小为：

式中LR是资料点距离库在径向上的单位长度，即雷达径向分辨率。

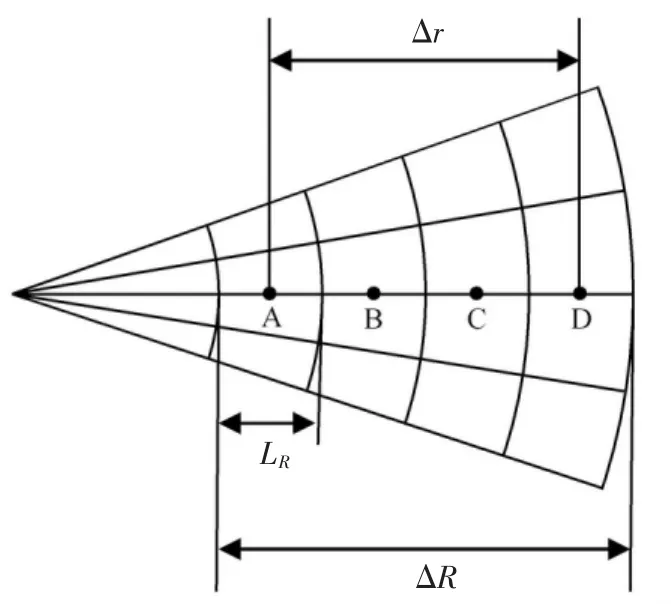
图1 一维径向风切变原理示意图

2.2.2 一维切向风切变

对于一维切向风切变(AS)，自适应拟合“窗口”包含n个距离库，即：

式中vi是“窗口”内第i个距离库的径向速度，θi是相应点的方位角。设v*为拟合“窗口”的速度估计值，则线性回归方程为v*=a+b(rθ)，r为该距离库与雷达之间的距离，仍利用最小二乘法得拟合曲线的斜率b为：

距离库内的数据是以该点为中心的采样体积内的平均值，采样体积与雷达波束宽度和脉冲宽度相关。如图2所示，相同探测距离上的A、D两点的径向速度的一维切向风切变为:

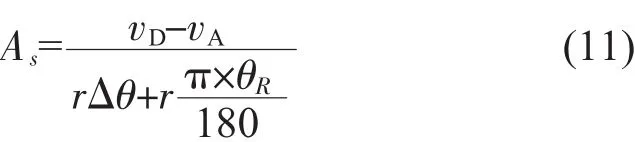
式中θR为雷达的角度分辨率(CINRAD/SA雷达的角度分辨率约为1°)，Δθ为弧度。

由于最小二乘法计算得到的斜率b为：

则一维切向低空风切变值AS为：

2.2.3 二维合成风切变

二维合成风切变定义为径向速度在径向、切向的综合变化，即一维径向风切变和一维切向风切变的合成。

2.3 垂直风切变算法

垂直风切变定义为多普勒雷达径向速度在距雷达相同距离，相同方位角处(即r、θ都是常数)上下两层PPI上随垂直高度的变化[12]，即：

式中，vp、vq为相邻上下两层PPI的径向速度，并进行了“窗口”为n的平滑拟合，Rp、Rq分别为上下两层的径向距离；αp、αq分别为上下两层PPI的仰角。当上下两层仰角的径向速度数据有任一缺失时不进行垂直切变计算，该点作为无资料处理。本文中“窗口”n取为3点，上下两层PPI径向速度分别取最低两层仰角(1.45 °和 0.53 °)。

2.4 时间风切变算法

基于多普勒雷达径向速度的时间风切变是指同一空间位置 (即径向距离R、仰角α和方位角θ都为常数)处时间间隔为Δt的前后两次低仰角PPI扫描径向速度随时间的变化，单位为m/(s·min)，即：

式中，vt1、vt2分别为同一空间位置处时间间隔Δt的前后两次PPI扫描的径向速度。当时间间隔为Δt的两次PPI数据中径向速度有任一缺失时不进行时间切变计算，该点作为无资料处理。由于新一代多普勒天气雷达VCP21模式下一次完整体扫需要6 min，为了计算第n-2次和第n次体扫的时间风切变，时间间隔Δt取12 min。

3 实例分析

本文利用两次天气过程的新一代多普勒天气雷达(CINRAD/SA)资料及MICAPS高空资料，进行风切变识别算法研究和验证分析。CINRAD/SA雷达的波束宽度为1.0°、探测距离为230 km、反射率因子数据的库长为1 km、径向速度数据的库长为250 m。在计算风切变之前，需对雷达基数据进行质量控制，以消除并纠正基数据中的错误。采用的方法是孤立噪声点[25]滤除、缺测数据填补和滤波平滑。本文使用郑佳锋[26]提出的“邻域频数法”的噪声点滤除与缺测值填补算法对反射率因子、平均多普勒速度进行处理。考虑到气象回波的连续性，为了进一步减少径向速度噪声，同时有效地保留径向速度中的小尺度结构，先对径向速度数据进行了3×3中值滤波，再沿径向和切向分别作5点、3点滑动平均。

3.1 实例1

2009年6月3日傍晚—4日凌晨，徐州及周边地区飑线过境，遭遇大范围雷雨、大风和冰雹等强对流天气，19个县市出现了17 m/s以上的短时大风。沙氏指数SI为-10.02℃，气团指标K为38℃，大气低层温度露点差较大，十分有利于强对流的发生，地面可能出现强低空风切变。

图3为2009年6月3日23:30(北京时间，下同)徐州站多普勒天气雷达回波图、PUP合成风切变识别产品及本文方法得到的时空四维风切变(二维合成风切变、垂直风切变及时间风切变)识别图。从0.53°仰角雷达回波图(图3a、3c)中可知，“人”字形飑线系统正在过境，飑线附近表现为活跃的雷暴带，这一区域反射率因子最大(45～60 dBz)，雷达站附近径向速度大于20 m/s。图中右边无层状云区的暖式飑线从雷达站周围向东延伸，左下方有层状云区的冷式飑线从雷达站向南延伸，相对于右边的暖式飑线，左下方的冷式飑线具有更加明显的飑线特征，反射率因子回波图中有明显的阵风锋细线回波，径向速度图中的阵风锋附近有明显的强切变线存在。

PUP合成风切变产品是利用1.45°仰角径向速度数据，基于直接计算差值滤波算法得到的。该算法先用差值法计算径向风切变和切向风切变，再经过滤波得到合成风切变[13]。为了作对比，本文的自适应多尺度合成风切变也采用1.45°仰角径向速度数据。图3e和图3f分别为同一时刻PUP合成风切变产品和本文的自适应多尺度合成风切变识别结果，显示阈值都为2.0×10-3s-1。可见，合成风切变大值区都出现在冷式飑线的前沿，在暖式飑线附近都没有明显的合成风切变，这与1.45°仰角径向速度图(图3d)中由阵风锋引起的风切变位置相吻合。相对于PUP合成风切变产品，本文的自适应多尺度合成风切变识别结果能有效地减少线性拟合的误差，滤除由于噪声导致的虚假合成风切变，回波边缘风切变识别更加合理，识别的风切变也更加连续。

图3g是0.53°仰角径向速度与1.45°仰角径向速度间的垂直风切变。可见，在左下方的冷式飑线后部出现负垂直切变最大值，冷式飑线前部出现正垂直切变最大值。说明在低层冷式飑线后部存在和飑线移动方向相同的径向速度，冷式飑线前部存在和飑线移动方向相反的径向速度。并且在阵风锋附近垂直风切变的水平梯度很大，在一定程度上也能反映飑线的位置。图3h是2009年6月3日23:18和2009年6月3日23:30之间0.53°仰角径向速度的时间风切变，显示阈值为0.5 m/(s·min)。可见，时间风切变大值区出现在阵风锋在12 min内移动经过的区域，所以时间切变可反映飑线在12 min内的移动情况。

综合分析图3可看到，合成风切变、垂直风切变和时间风切变构成的时空四维风切变识别图中，切变发生的位置与雷达径向速度图中飑线的位置有较好的对应关系，风切变识别结果较理想，可为民航机场低空风切变预警提供一定的帮助。

图3 2009年6月3日23:30徐州飑线过程多普勒天气雷达回波及低空风切变识别结果

3.2 实例2

2017年6月5日西南低空急流造成南京及周边地区出现大范围大风、降水天气。图4a是6月5日08时850 hPa天气图。可见，南京地区位于西南急流中心的左前方，该区域由于涡度平流引起的垂直运动造成上升运动最强，并且该区域与温度场中的暖舌相结合。图4b是6月5日08时南京站单站高空风图，从圆心到该点的距离表示风速大小，从圆心指向该点的矢量表示风的来向，可见在850 hPa附近存在风速的极大值，大于20 m/s，达到低空急流的风速标准，风向随高度增加顺转，出现暖平流。

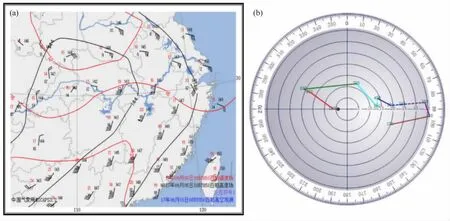
图4 2017年6月5日08:00 850 hPa天气图(a)和南京站单站高空风图(b)

图5 (见下页)为2017年6月5日12:01南京站多普勒天气雷达回波图、PUP合成风切变识别产品和本文方法得到的时空四维风切变 (二维合成风切变、垂直风切变及时间风切变)识别图。强降水区域的回波强度为20～45 dBz，没有明显的强对流。径向速度图(图5b)中，零径向速度线呈正“S”形，风向随高度顺转，风速随高度增加先增加后减小，在雷达站西北方向46～92 km附近存在正径向速度中心，在雷达站东南方向46～92 km附近存在负径向速度中心，在距雷达站80 km(高度约2 km，即850 hPa等压面)附近存在明显的风切变。这与上述的天气学分析结果基本吻合。

图5c和图5d分别是1.45°径向速度对应的PUP合成风切变产品和本文的自适应多尺度合成风切变识别结果，显示阈值都为2.0×10-3s-1。切变大值区与径向速度图中切变线位置吻合良好，本文方法得到的合成风切变相对于PUP的合成风切变产品，有效地滤除径向速度自身波动引起的虚假风切变，回波边缘识别结果更可靠。在切变线西侧存在负垂直切变大值区(图5e)，说明上层负径向速度增强，正径向速度减弱。图5f是2017年6月5日11:49和2017年6月5日12:01之间1.45°仰角径向速度的时间风切变，显示阈值为0.5 m/(s·min)。可见，时间风切变大值区同样和径向速度图中切变线的位置对应较好，相对于飑线过程，低空急流引起的时间风切变值较小，说明该天气过程相对于飑线系统移动较慢。

4 结论与讨论

本文研究了利用地基多普勒天气雷达基数据识别低空风切变的方法，并通过徐州一次飑线过程及南京一次混合云降水过程的实例从时空四维空间上验证了低空风切变识别算法的有效性。

(1)对雷达径向速度资料进行一定尺度的滤波和平滑，可有效地消除径向速度自身波动产生的噪声，并保留产生低空风切变的中小尺度风信息。

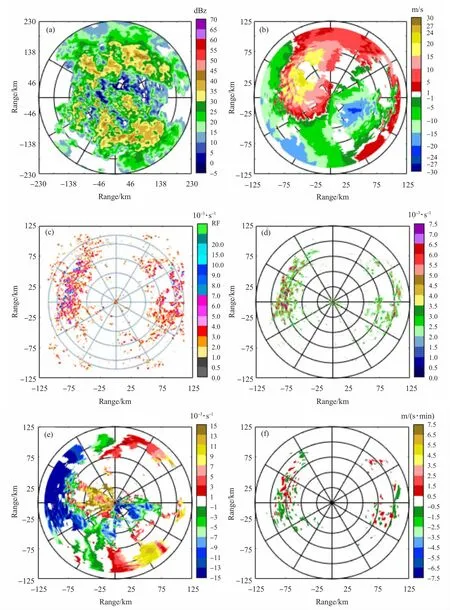
图5 2017年6月5日12:01南京混合云降水过程多普勒天气雷达回波及低空风切变识别结果

(2)基于风切变强度因子的最小二乘法自适应拟合“窗口”的选取可有效地减少人为主观性，降低单一窗口尺度造成的低空风切变漏报现象。

(3)相对于PUP二维合成风切变产品，本文方法得到的合成风切变在切变连续性、切变识别效果和边缘虚假切变处理等方面更优，与雷达径向速度图中风切变的位置相吻合。

(4)垂直风切变可反映径向速度的高低空配置情况，时间风切变可提供径向速度随时间的变化情况。

利用多普勒雷达径向速度数据从合成风切变、垂直风切变和时间风切变四维空间实现对低空风切变的自动识别，可为民航机场低空风切变预警提供有效的辅助工具。需要指出的是，由于多普勒雷达探测的是取样体积内的平均径向风，并且空间分辨率有限，很难准确反映真实的三维风场特性，因此，这里识别的低仰角径向速度的低空风切变是真实风场的低空风切变的近似，两者之间可能稍有差异。另外，本文未考虑速度模糊现象，算法的预处理过程还值得进一步改进和优化。