半干旱区湍流相干结构对地表能量不平衡问题的解决

赵建华 王介民 张强 周悦

摘 要：地表能量不平衡是近30年来来微气象学界面临的难题。综合前人的研究成果，我们认为涡动相关法的基础——雷诺平均对地表能量不平衡有重要影响。雷诺平均存在的问题在于其忽视了湍流的间歇性与相干结构。为此，在考虑此两因素的基础上，我们提出了大涡平均法替代雷诺平均来进行流动分离。采用中国气象局兰州干旱气象研究所定西干旱气象与生态环境试验基地的湍流观测资料计算后发现，进行大涡平均后，湍流脉动场可以有效去除雷诺平均后残存的线性趋势和涡结构，而且也可以再现惯性子区的-2/3方律，在温度方面甚至优于雷诺平均。接着，对比分析了两种平均方法在计算均值与通量时的关系，发现两法的结果存在显著的线性相关，雷诺平均会低估平均垂直速度、动量垂直通量、热量垂直通量与水汽垂直通量、感热与潜热，高估水平速度、温度与水汽密度;总体而言，大涡平均的垂直通量要比雷诺平均的大12-18%。我们得到了两法计算的感热与潜热等垂直通量的线性关系，将之带入到地表能量平衡方程中，结果发现地表能量平衡的闭合度可以提高11%左右。如果地表土壤热通量采用四边形法计算的话，则闭合度在上白天、下白天和整个白天均为1.01，这意味着，地表能量至少在半干旱区的夏季白天实现了平衡。

关键词：地表能量平衡;间歇性;相干结构;大涡平均;雷诺平均

中图分类号：P404 文献标识码：A 文章编号：1671-2064（2019）06-0248-09

0 引言

地表能量不平衡是30多年来微气象学界普遍面临的难题。许多研究从各个方面进行了研究，比如仪器精度、观测误差、坐标旋转与平面拟合、footprint效应、WPL订正、涡动相关法精度[1，2]、土壤热对流[3]、位相差异[3-5]、热储存[5-7]、考虑包括低频涡在内的各种尺度涡的贡献[1，2，，5，8-10]以及垂直感热平流[11]。虽然取得了许多成果，但是不管是平坦地形还是复杂地形，地表能量依然不平衡。一般认为，地表能量不平衡是随着基于快速响应探头的涡动相关法的广泛应用而出现的，而涡动相关法被认为是观测湍流通量的最优方法[12]。涡动相关法的精度也一度被微气象学界认为是地表能量不平衡的重要原因[1，2，12]。综合考虑前人的各项研究成果，尤其是考虑到学界目前的认识方向：各种尺度涡的贡献在涡动相关法的考量，使我们认识到很有可能是湍流的分离出现了问题，也就是涡动相关法的基础——雷诺平均出现了问题。

1875年雷诺提出了著名的雷诺平均分解理论[13]，物理场可以分解为缓变的平均场与快变的湍流因子，该理论对湍流的发展具有重要的意义。但雷诺平均并不是普适的，它满足一定的条件[14]，也即意味着它有适用性。Andreas（1988）[15]给出了雷诺平均的平均时间满足的公式。de Feriet[16]对雷诺平均提出了质疑，发现它的条件并不容易满足。Randall[17]考虑了滑动平均、格体平均（grid-cell averages）与系综平均（ensemble averages）这三种平均算符，发现这些条件在实际流體中并不容易满足，且并不一致。Trevio and Andreas[18]指出雷诺平均在估计湍流时间序列均值时需要满足平稳与不相关的条件。高歌[19]将流场中一点处的速度脉动分为Ⅰ、Ⅱ两组分别进行平均，其平均值均不为零，这也正是考虑到单纯的雷诺平均存在缺陷所致。正如张兆顺等[20]所说，雷诺平均模型的致命弱点是它的模型没有普适性。这些表明，雷诺平均并没有反应出流动的内在特征。

雷诺平均的本质是流动分解。湍流是多尺度运动，既有大尺度运动，也有小尺度运动，决定了雷诺平均在流动分离上的困难，也即雷诺平均实际上没有将层流与湍流分离开来，而是两者相互混杂流动的简单尺度分离，并不是不同类型的流动分离，也即是它这种分离是层流与湍流的混合体。湍流还具有间歇性，但是雷诺平均却并不考虑此间歇性，它总是以为湍流发生在整个平均时间段上，这显然会造成层流与湍流的混叠，从而导致其可靠性降低。雷诺平均还有一个重要问题是，基于其得到的湍流基本方程一直存在着闭合的问题，迫使科学家想尽办法从理论与经验各个方面进行闭合。由于湍流的多尺度性，决定了普适的平均湍流输送量的闭合方程不可能建立[20]。另外，实践也发现，雷诺平均在实践中计算精度较低[21]，数值实验证明雷诺平均方法在模拟复杂流动现象如涡脱落、浮力影响、流线弯曲、旋转和压缩运动时会遇到难以克服的困难[22]，它并不像后来产生的大涡模拟那样可以模拟出较高雷诺数和较复杂的湍流运动，而大涡模拟可以提供大涡结构信息等更多的湍流信息，也可以提高雷诺平均N-S方程的模拟[23，24]，大涡模拟在复杂流动的模拟中可以得到很多雷诺平均方法无法获得的紊流运动的细微结构和流动图像[22]。这些意味着雷诺平均在理论与实践中具有不可克服的缺陷。

在地表能量不平衡的研究实践中，发现不同的平均时间，会造成湍流高低频信号的差异，平均时间过短则造成低频损失，过长则不易捕获湍流细节[25]。梁捷宁等[26]指出，使用涡动相关资料研究湍流通量时，定义湍流的平均时间内的运动是造成湍流统计量变化范围大的主要原因。Campos等[27]指出计算地面通量的平均时间尺度或时间窗是极端重要的因子。Finnigan等[28]和Cava等[29]发现尺度延伸到4hr的涡仍会有9%的脉动通量贡献。大涡模拟也揭示中尺度涡旋和湍流拟序结构的通量可以部分解释地表能量平衡的欠闭合部分[8，12，30，31]。因而经验模态分解也用来提高涡动相关法估算湍流通量的精度[10，32，33]。

流动分离需要考虑湍流的特征、结构、发生及演变。湍流具有间歇性，但是雷诺平均并不考虑这种特性，这必然导致其具有不准确性。另外，无论从最初雷诺的圆管实验[36]，到Townsend[37]大涡实验和Kline等[38]的氢气泡实验，还是湍流的串级理论[39]以及各种尺度涡的叠加运动等认识，无不在揭示着湍流是涡的本质，而包括准流向涡、发卡涡和涡包[40]或者从形态上分的线涡、涡环、发卡涡与螺旋涡[41]在内的相干结构作为湍涡的体现者，在湍流的产生与输送中占有重要作用[34，35]。我们认为，相干结构作为湍流中的有序结构（相干结构由此可定义为湍流中所有的、处于湍流尺度中的有序涡结构），是湍流的实际产生者，湍流的产生就是相干结构的产生，其消亡也可以看做是相干结构的消亡;串级过程与次尺度湍涡都可看成是相干结构的结构或演变[42]，故可直接将相干结构看作是湍流，这样就可以直接以相干结构研究湍流，湍流从而变得简单。大气边界层中普遍存在着相干结构，气象学家对相干结构给出的定义是与高频小尺度湍流具有相互作用的、位相相关的、有组织的、非周期低频大尺度运动，常能保持其特征形式，并具有一定的间歇性[43-45]，它普遍存在于稳定、中性和不稳定大气层结中，也存在于各类植被冠层中[44，45]。我们认为，这种具有间歇性的相干结构的存在会对雷诺平均产生重要影响，忽视相干结构是雷诺平均不准确的根本原因，这也是地表能量不平衡的根源。本文即对此展开研究，以期获得相干结构对地表能量不平衡的影响。

1 数据与方法

1.1 测站和数据

测站位于中国气象局兰州干旱气象研究所定西干旱气象与生态环境试验基地。该基地经纬度坐标是（104°37E，35°35N），海拔高度为1896.7m，年平均温度为6.7℃，降水量为386.0mm，日照时间为2433hr，属典型的半干旱区。基地南北两侧各有一座东北——西南走向的山，基地距北山直线距离为750m左右，距南山直线距离800左右。基地地势平坦，周围分布有农田与低矮建筑物。观测期间，下垫面为均匀分布的马铃薯，株高约50cm。

基地主要由微气象塔梯度观测系统、涡动相关系统、辐射平衡观测系统土壤温湿度和热通量观测系统构成。本文主要采用由安装在距地面2.5m高度处的美国Campbell公司生产的三维超生风速仪CSAT3与Licor公司生产的二氧化碳/水汽分析仪LI-7500采集的数据。该数据质量良好，在地表能量平衡以及估算感热潜热的研究中得到了良好应用[35-37]。另外，还采用了微气象塔梯度观测系统观测的降水资料，该资料用以去除降水的时段。数据采集器为Campbell公司的5000和cr23xcr，相关系统采样频率为10Hz，降水资料分辨率为半小时。数据时段从2011年7月1日到同年8月10日结束。

1.2 方法

雷诺平均本质上是流动分离算子。湍流虽然包含有组织的结构（比如相干结构），但是这些结构的产生具有一定的过程，背景流动为这些组织的产生提供了必不可少的物质与能量。有组织结构的产生最重要的是相干结构，Hussian[46]给出一个相干结构的广泛定义：相干结构是某一特定区域上的具有瞬时相位相关的涡旋的相互衔接的湍流质[46，47]，简单说也就是相干结构是湍流中所有的、处于湍流尺度中的有序涡结构。有的文献中把相干涡和其边界与背景流动的交互作用产生的有序结构也叫作相干结构，此处我们专指相干涡，这符合湍流是各种尺度湍涡的综合效应的认识。许多研究表明，湍流在时空分布上并不是平稳、均匀的，而是具有间歇性，也即相干结构的间歇性。间歇性与大尺度相干结构密切相关[48]。因此，流动分离需要考虑湍流的间歇性;不考虑间歇性，显然会产生误判，这是雷诺平均一个很重要的缺陷。另外一点是，在流动分离时需要考虑相干结构的合并，此合并产生的涡记为大涡。涡的合并在射流与壁湍流中均有观测，比如涡包，涡包是一连串的发卡涡组成，由大的发卡涡引领次第产生的尺度更小的新发卡涡排列一线组成，Adrian & Marusic[49]认为发夹涡群是紊流猝发的本质，是维持湍动能的基础，發夹涡群的不断重叠形成了大尺度的准流向涡结构，而非二次流。在大气边界层中也存在着尺度更大的有组织的低频涡或较大尺度涡旋[8，12]，如卷流和热泡。有研究指出，大涡本质上就是相干结构的叠加涡——涡包[50]。许多研究发现[27]，对大气边界层湍流数据进行30min平均基本上可以包含各种尺度湍流的贡献，这意味着30min平均时间可能正是这个大涡的周期。这些大涡的产生与背景流和相干结构密切相关，后两者是其形成所需要的物质与能量的提供者。这也就意味着，在其形成中包含着相干结构这种湍流和非湍流的背景流。以雷诺平均进行分离（假设雷诺平均的尺度恰好是此大涡的尺度），此时如果这个大涡处于孕育期或未成熟期，则必然有部分背景流未被大涡同化或吸收进去，必然造成雷诺平均这种分离法产生如前一样的结果：湍流非湍而均流非均，即湍流中含有背景流，背景流中含有湍流;从数学上，平均值不尽是背景流的，脉动值也不尽是湍流的。不必担心此平均中相干结构的影响，因为它本身就是湍流，它与大涡是同质的，它是大涡的基本构成单位。当然，如果大涡发展成熟且稳定，则此平均原则上可以正确分离流动。由于在大气边界层中，尤其是白天晴天，大涡可能难以形成为一个稳定成熟的状态，它一直处于壮大（上白天）或缩小（下白天）的过程之中，即它一直处于动态变化中，因此单纯的线性的雷诺平均是很难干净地分离出背景流与湍流。合理的做法应该是以大涡的构成因子——相干结构进行平均，即在大涡或相干结构（如大涡没形成或尺度较小时）的尺度上，基于湍流质——相干结构进行平均，即可干净地得到背景流动值与湍流脉动值。我们称此平均法为大涡平均，它与大涡模拟的思路是一致的。其表示如下：

（1）

其中，是相干结构的数目，是基于相干结构的雷诺平均，是大涡平均。采用这种方法时，首先需要检测出相干结构，这是其条件。脉动值此时为

（2）

代表了构成大涡或相干结构的流元的湍流运动，组成大涡的背景流所应有的湍流运动也被它正确描述。

具体实现时，本文事先按照文献[45]的方法确定出相干结构，然后按照（1）（2）式获得大涡平均值与脉动值。雷诺平均值与其脉动值采用教科书通用方法，即求30min时段内的平均与偏差。另外，对于地表能量平衡的计算，直接对我们前期的结果[5]按照后面的公式（8）（9）进行订正获得，具体方法参见文献[5]。

2 结果

2.1 脉动场与平均场的演变

图1是雷诺平均与大涡平均后脉动值的演变。可以发现，采用雷诺平均，脉动值还具有一定的线性趋势，而且还存在明显的涡结构;而采用大涡平均后，线性趋势消除了，涡结构也不再显著。很显然，大涡平均法优于雷诺平均法。

在图2中，基本上每个平均值对应着一个相干结构，相干结构数目较多，持续时间较短。当然，这是在正午的情况，夜间的相干结构数目少很多，不过持续时间较长（图略）。平均值存在跳跃的现象，这反映了平均场不连续的特征。平均水平速度（图2a）与平均水汽密度（图2d）呈现出正弦波的变化，且位相基本相同，表现了平均流场的变动形式与水汽的水平分布。伴随着这种波动，出现了空气的垂直升降运动（图2b），也即是出现了空气的辐合辐散。平均气温（图2c）与平均气压（图2e）趋势相反，同样表明了平均温压场的一种分布，也即东风为主（图2a）的情况下，温度较高，气压较低。

2.2 湍流谱分析

Kolmogorov指出[50]，在惯性副区中湍流能谱正比于ε2/3 k-5/3，ε是湍流能耗率，k是波数。该表达式以观测中的频率可表示如下的k的-2/3次方律[50]：

（3）

（4）

式中，是速度能谱，是温度能谱，是频率，是观测高度，是平均速度。

速度与温度的湍流谱（图3）显示，存在明显的-2/3指数律，惯性子区是存在的。高频段的上翘部分对应的是耗散区，这种上翘见诸于诸多文献[50，51]。另外，结果显示（图略），采用雷诺平均时温度的湍流谱并不符合-2/3指数律，而大涡平均法则完整的显示了这一特征。显然，大涡平均法是有效的。

2.3 雷诺平均与大涡平均的单要素均值比较

无论速度、温度还是水汽密度，大涡平均与雷诺平均呈极为显著的线性关系，只是除了垂直速度外，其余变量（水平速度、温度与水汽密度）雷诺平均值略大些。这是由于雷诺平均法一方面重复计算均值，另一方面重复计算的同时又在对背景流动进行过滤，对背景流动进行分离，这样累计的效果就是使得雷诺均值与实际不同。大涡平均的垂直速度较大，表明雷诺平均低估了垂直速度。另外，两法的垂直速度虽也线性相关，但较离散，这一方面是由于垂直速度一般较小，对平均方法比较敏感，另一方面，背景尺度的波动影响不可忽视，如图4所示。

2.4 雷诺平均与大涡平均的通量比较

图5是两法计算的动量通量、热通量、水汽密度通量（均是垂直方向）、感热与潜热的对比。可以发现，两法的通量线性关系非常显著，不过大涡平均法计算的通量普遍比雷諾平均法的大12-18%，这意味着雷诺平均在实际中是低估了包括感热与潜热在内的各种垂直通量。雷诺平均法的低估应该主要是由于对垂直速度低估引起。

下面是两法通量的线性关系：

（5）

（6）

（7）

（8）

（9）

其中，、、、与分别是动量垂直通量、热量垂直通量、水汽密度垂直通量、感热与潜热。

2.5 地表能量的平衡

地表能量平衡一般指的是在土壤、空气水平分布均匀的前提下，净辐射、土壤热通量、感热、潜热以及包括土壤在内的热储存之间的能量平衡，公式如下：

（10）

其中，、和分别是净辐射、某一深度处土壤热通量以及土壤、空气与植被的热储。在本试验的半干旱区，空气热储存与植被热储存很小[6，7，53]，可忽视，此时仅为土壤热储。这是在水平分布均匀情况下的公式，如果不均匀，则还需要考虑水平方向的能量平流。（10）式的左侧称为湍流热通量，右侧称为可利用能量。

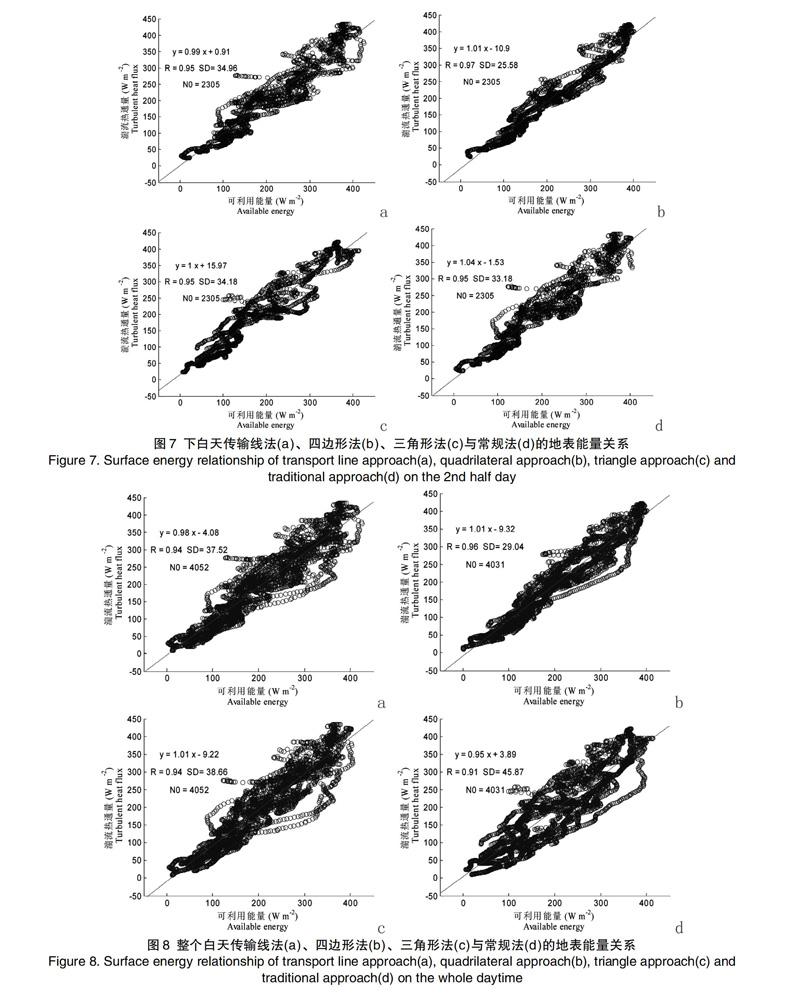
我们曾经考虑了常规法和考虑慢过程的传输线法、四边形法与三角形法等4种方法的地表能量平衡问题（4种方法均考虑了土壤热储，文献[5]），这4套方法均是采用雷诺平均计算的感热与潜热，结果是常规法求得的地表能量的闭合度分别为0.87、0.93与0.91（分别对应上白天、下白天和整个白天，下同。均值为0.90），考虑慢过程的传输线法分别为0.86、0.89和0.88（均值为0.88），四边形法分别为0.92、0.90和0.91（均值为0.91），三角形法分别为0.88、0.90和0.85（均值为0.88）[5]。现在，根据上节定出的雷诺平均法与大涡平均法的感热、潜热的关系（公式（8）、（9）），可以研究地表能量平衡。以公式（8）与（9）换算得到新的感热与潜热，代入公式（10）中，结果见图6-8。

由图可见，采用大涡平均法计算感热与潜热后，传输线法、四边形法、三角形法和常规法在上白天的地表能量闭合度分别提升到0.95、1.01、0.98和0.97（图6），在下白天分别提高到0.99、1.01、1.0和1.04（图7），在整个白天分别提高到0.98、1.01、1.01和0.95（图8），提高了大约4-19%，平均提高11%。显然，这种提高是很大的，提高的结果使地表能量趋于平衡。注意的是，考虑慢过程的传输线法、四边形法和三角形法的闭合度（均值分别是0.97、1.01、1.0）总体上比常规法（均值为0.99）要好，而其中尤为注意的是四边形法（当然三角形法结果也比较好），该法在上白天、下白天和整个白天的闭合度均为1.01。这是一个好的结果，这意味着，如果采用四边形法计算代表土壤热通量，再采用大涡平均法计算感热与潜热，则在半干旱区夏季，地表能量可以达到平衡。另外，即便采用其它方法，地表能量的闭合度也在接受范围之内。所以，本文实现了地表能量在半干旱区的平衡。

3 结语

本文通过分析雷诺平均的内在缺陷，对雷诺平均的准确性进行了质疑，认为雷诺平均对间歇性与相干结构的忽视是其不准确的内因。在此基础上，提出了能够分离流动的大涡平均法，基于该方法本文对比分析了脉动场、湍流谱、单要素均值以及通量的关系，得到了大涡平均与雷诺平均的感热与潜热的线性关系，最后以此关系分析了半干旱区的地表能量平衡问题，得出了地表能量可以平衡的结论。主要结果如下：

（1）雷诺平均忽视了湍流的间歇性与相干结构，造成其在分离流动时存在错误。

（2）提出了大涡平均法替代雷诺平均方法以分离湍流，该法可以有效消除湍流脉动场的趋势与雷诺平均不能过滤的涡结构，而且能再现惯性子区湍流谱的-2/3方律。

（3）大涡平均与雷诺平均的单要素均值存在非常显著的线性关系，雷诺平均低估平均垂直速度、高估平均水平速度、温度与水汽密度。

（4）两法的动量垂直通量、热量垂直通量、水汽密度垂直通量、感热与潜热线性关系显著，但是雷诺平均一般低估这3个通量，低估达12-18%。

（5）采用大涡平均法计算的感热与潜热后，地表能量闭合度平均可提高11%左右。具体为：考虑土壤热量传递慢过程的传输线法、四边形法与三角形法以及不考虑慢过程的常规法的闭合度平均为0.97、1.01、1.0和0.99，均非常接近1.0，其中尤以四边形法结果最好，该法在上白天、下白天和整个白天的闭合度均为1.01。这些结果表明，本研究实现了地表能量在半干旱区夏季的平衡。

上述结果意味着，采用大涡平均法可以在半干旱区夏季实现地表能量的平衡，由此，地表能量不平衡问题至少在半干旱区夏季的白天得以解决。我们预估：如果考虑充分，计算准确（比如采用四边形法计算土壤热通量与采用大涡平均法计算感热、潜热），则地表能量在其它时段与地区也应该是平衡的。另外，需要说明的是，采用大涡平均法替代雷诺平均法分离流动，这将导致湍流的基本方程（比如脉动方程与平均方程）都需要改写，基于雷诺平均的各种关系式也需要改写。

致谢：诚挚感谢中国气象局兰州干旱气象研究所岳平博士与张良博士的帮助。

参考文献

[1] Sakai RK，Fitzjarrald DR，Moore KE.）Importance of low-frequency contributions to eddy fluxes observed over rough surfaces[J].J Appl Meteorol，2001，40（12）：2178-2192.

[2] Foken T，Aubinet M，Finnigan JJ，et al.Results of a panel discussion about the energy balance closure correction for trace gases[J].Bull Am Meteorol Soc，2011，92（4）：ES13-ES18.

[3] Gao Z，Horton R，Liu H P.Impact of wave phase difference between soil surface heat flux and soil surface temperature on soil surface energy balance closure[J].J Geophys Res Atmos，2010，115，D16112，doi：10.1029/2009JD013278.

[4] 岳平，張强，赵文，等.黄土高原地表能量闭合特征及土壤通量参数化[J].冰川冻土，2012，34（3）：583-590.

[5] 赵建华，张强，王胜等.半干旱区土壤热量传递的慢过程对地表能量平衡的影响[J].土壤通报，2013，44（6）：1321-1331.

[6] Wang R Y，Zhang Q.An assessment of storage terms in the surface energy balance of subalpine meadow in northwest China[J].Advance in atmospheric science，2010，28（3）：691-698.

[7] 李宏宇，张强，赵建华，等.陇中黄土高原地表能量不平衡特征及其影响机制研究[J].高原气象，2010，29（5）：1153-1162.

[8] 王介民，王维真，刘绍民，等.近地层能量平衡闭合问题—综述及个例分析[J].地球科学进展，2009，24（7）：705-713.

[9] Foken T.The energy balance closure problem： An overview[J].Eco Appl，2008，18（6）：1351-1367.

[10] Barnhart B， Eichinger W， Prueger J. A new eddy-covariance method using empirical mode decomposition[J].Boundary-Layer Meteorol，2012，145（2）：369-382.

[11] 张强，李宏宇，赵建华.垂直平流输送和土壤热储存补偿对黄土高原地表能量平衡的修正[J].中国科学：地球科学，2011，41（12）：1-10.

[12] 陈家宜，范邵华，赵传峰，等.涡旋相关法测定湍流通量偏低的研究[J].大气科学，2006，30：423-432.

[13] Reynolds O.On the Dynamical Theory of Incompressible Viscous Fluids and the Determination of the Criterion[M]. Philosophical Transactions of the Royal Society of London，A，1895，pp.123-164.

[14] Monin A S and Yaglom A M.Statistical fluid mechanics，Vol.1[M].Mechanics of turbulence.MIT Press，Cambridge，Mass.，1971，769pp.

[15] Andreas E L.Estimating averaging times for point and path-averaged measurements of turbulence spectra[J].J Applied Meteorology，1988，295-304.

[16] de Feriet J K.Avraging processes and Reynolds equations in atmospheric turbulence[J].J Meteorol，1951，358-361.

[17] Randall D.Reynolds Averaging[J].Quick studies for graduate students in Atmospheric Science，2016，26，1-8.

[18] Trevio G and Andreas E L.On the Reynolds averaging of turbulence time series[J].Boundary Layer Meteorol.，2008，128，303-311.

[19] 高歌.Gao_Yong理性湍流方程[J].推进技术，2010，31（6）：666-675.

[20] 张兆顺，崔桂香，许春晓.湍流大涡数值模拟的理论和应用[M].清华大学出版社，2008，pp54-89.

[21] 陈逖，刘卫东，孙明波，等.超声速湍流边界层中横向声速喷流的混合LES/RANS模拟[J].航空动力学报，2013，28（11）：2536-2542.

[22] 王玲玲.大涡模拟理论及其应用综述[J].河海大学学报（自然科学版），2004，32（3）：261-265.

[23] Zeng Z，Sun D，Zhou L.Comparison of gas particle flow prediction from large eddy simulation and Reynolds-averaging Navier-Stokes modeling[J].J Shanghai Jiaotong University （Science），2010，15（5）：622-625.

[24] 王帅.气固两相流气相亚格子模型效应的研究[J].哈尔滨工业大学，硕士论文，2010.

[25] 呂少宁，文军，张宇，等.不同平均时间对LOPEX10资料涡动相关湍流通量计算结果影响的探讨[J].高原气象，2012，31（6）：1530-1538.

[26] 梁捷宁，张镭，鲍婧，等.黄土高原复杂地形受中尺度运动影响的稳定边界层湍流特征[J].大气科学，2013，37（1）：113-123.

[27] Campos JG，Acevedo OC，Tota J，et al.On the temporal scale of the turbulent exchange of carbon dioxide and energy above a tropical rain forest in Amazonia[J]. J Geophys Res Atmos，2009，doi：10.1029/2008JD011240.

[28] Finnigan J J，Clement R，Malhi Y et al.A re-evaluation of long-term flux measurement techniques.Part I：averaging and coordinate rotation[J].Bound Lay Meteorol，2003，107：1-48.

[29] Cava D，Contini D，Donateo A et al. Analysis of short-term closure of the surface energy balance above short vegetation[J].Agr Forest Meteorol，2008，148：82-93.

[30] Kanda M，Inagaki A，Letzel M O.Les study of the energy imbalance problem with eddy covariance fluxes[J].Bound Lay Meteorol，2004，110：381-404.

[31] Inagaki A，Letzel M O，Raasch S，et al.Impact of surface heterogeneity on energy imbalance：A study using LES[J].J Meteor Soc Japan，2006，84（1）：187-198.

[32] Wang，J.，Song，J.，Huang，Y.et al. Application of the Hilbert–Huang Transform to the Estimation of Air-Sea Turbulent Fluxes[J].Boundary-Layer Meteorol，2013，147：553-568.

[33] Martins LGN， Miller SD， Acevedo OC. Using Empirical Mode Decomposition to Filter Out Non-turbulent Contributions to Air–Sea Fluxes[J].Boundary-Layer Meteorol， 2017，163：123-141.

[34] 陈懋章.粘性流体力学基础[M].北京：高等教育出版社.2002，pp282-286.

[35] Cooper D I，Leclerc M Y，Archuleta J，et al. Mass exchange in the stable boundary layer by coherent structures[J].Agric For Meteorol，2006，136：114-131.

[36] 怀特 F著，魏中磊，甄思淼译.粘性流体动力学[M].北京：机械工业出版社，1982，pp425-432.

[37] Townsend A A.The structure of turbulent shear flow（1st edn）[M].Cambridge University Press，1956，pp1-442.

[38] Kline S J，Reynolds W C，Schraub F H，et al.The structure of turbulent boundary layer[J].J Fluid Mech，1967，30：741-774.

[39] Richardson L F.Weather Prediction by Numerical Press[M].Cambridge： Cambridge University Press，1922，pp1-236.

[40] 范宝春，董刚，张辉.湍流控制原理.北京：国防工业出版社.2011，pp78-98.

[41] 邱翔，刘宇陆.湍流的相干结构.自然杂志，2004，26（4）：187-193.

[42] 赵建华，张强.二维均匀剪切湍流的湍涡闭合方案[J].干旱气象，2010，28（1）：8-19.

[43] Barthlott C，Drobinski P， Fesquet C， et al.Long-term study of coherent structures in the atmospheric surface layers[J].Boundary-Layer Meteorol.，2007，125：1-24.

[44] Paw U K T， Brunet Y，Collineau S，et al.On coherent structures in turbulence above and within agricultural plant canopies[J].Agric.For.Meteorol，1992，61：55-68.

[45] Zhang Y，Liu H，Foken T，et al.Coherent structures and flux contribution over an inhomogeneously irrigated cotton field[J].Theor.Appl. Climatol，2011，103：119-131.

[46] Hussian A K M F.Turbulence and chaotic phenomena in Fluids（ed.T.Tatsumi）[M]. North-Hellao，1983，pp179.

[47] 王发民.湍流中的相干结构[J].中国科学基金，1990，1：29-37.

[48] 陈京元，陈式刚，王光瑞.大气湍流间歇性及其对光波传播的影响[J].物理学进展，2005，（4）：386-406.

[49] Adrian R J，Marusic I.Coherent structures in flow over hydraulic engineering surfaces.Journal of Hydraulic Research，2012，50（5）：451-464.

[50] Guala M， Hommema S E，Adrian R J.Large-scale and very-large-scale motions in turbulent pipe flow.J.Fluid Mech.，2006，554：521-542.

[51] 劉树华，李洁，刘和平，等.在EBEX-2000实验资料中湍流谱和局地各向同性特征[J].大气科学，2005，29（2）：213-234.

[52] Gotoh T. Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation[J]. Physics of Fluids，2002，14（3）：1065-1081.

[53] 李宏宇，张强，赵建华.论地表能量不平衡的原因及其解决办法[J].干旱区研究，2012， 29（2）：222-232.

[54] Meinhart C D and Adrian R J.On the existence of uniform momentum zones in a turbulent boundary layer [J].Phys. Fluids，1995，7：694-696.

[55] Zhou J，Adrian R J，Balachandar S，et al.Mechanisms for generating coherent packets of hairpin vortices in channel flow [J].J.Fluid Mech.，1999，387：353-396.