WSN中一种流水式栅栏调度算法的研究*
2019-05-08戴光麟杨志凯周贤年陈立建毛科技
戴光麟,杨志凯,周贤年,陈立建,毛科技
(浙江工业大学计算机科学与技术学院,杭州 310032)
无线传感器网络WSN(Wireless Sensor Networks)被多个行业广泛使用[1-2],在这当中,无线传感器网络栅栏覆盖大部分被应用于入侵者检测。如在环保方面,可检测污染物的扩散情况。在国防应用中,可对越境者进行自动化探测。在林业保护方面,可预警、并且对火灾蔓延情况进行探测等[3-4],但同时,硬件设施方面对发展在很大程度上限制了传感器节点的使用。因此通过软件算法来延长传感器网络的生存时间成为了非常关键的研究问题。
为了延长栅栏的生存时间,目前主要通过研究三大块方向来实现。在栅栏调度方面,如Kumar等人提出了Optimal Sleep-Wakeup调度算法,该算法通过分析栅栏的生存时间,组合成若干组k-栅栏,使得栅栏的能量被充分利用,从而达到k-栅栏生存时间最大化[5]。Kim K S等人提出了Duty-Cycle Scheme调度算法,该算法通过轮流调度多条栅栏,使得在保证一定监测率的情况下延长了网络的生存时间[6-7]。文献[8-13]等都研究了在不同情况下的延长栅栏生存时间的方法。从栅栏的加强和修复方法来看,其主要原理是使死亡的栅栏重新工作。Anwar Saipulla等人提出一种二阶段算法修补栅栏间隙法。第1阶段,FIND-GAPS算法查找栅栏间隙,第2阶段MEND-GAPS算法修复栅栏[14]。Xu B等人研究分析入侵的历史数据,分析得到栅栏中的易受攻击点,然后通过移动节点来加强这些易受攻击的位置的栅栏,从而防止因为某些节点能量消耗过多而导致栅栏提早死亡[15]。Park T等人提出了一种寻找栅栏瓶颈区域,并在瓶颈区域内增加传感器节点的算法,从而延长了传感器网络的生存时间[16]。
由于不同WSN栅栏应用中对检测率的需求不同,本文提出了一种流水式的栅栏调度算法FSA(Flow-style Scheduling Algorithm),首先将栅栏均匀分割为些许子栅栏,将子栅栏循环激活,形成一种流水式工作状态,通过被激活状态的子栅栏来检测试图通过栅栏的入侵者。该算法在确保一定检测率的情况下实现栅栏生存时间的大幅度提高。
1 流水式栅栏调度算法
首先描述下要实现本文算法所需要的一些条件,本文假设栅栏已经由文献[17]等栅栏构建方法构建完成,然后进行算法描述。
1.1 相关条件
要实现本文算法的相关条件有四条:
条件1 传感器网络中节点同构,节点能量,感知半径等都相同。且节点只有处于激活状态时才会消耗能量,节点状态切换消耗的能量忽略不计。
条件2 某条子栅栏监测到入侵者后可直接与Sink节点通讯,不需要经过其他节点转发,且传感器节点可获取自身的位置信息(坐标)。
条件3 子栅栏不需要外部信号,直接通过节点内部的定时器设置唤醒与休眠状态的切换。
条件4 不考虑入侵者实际体积,将入侵者视为一个点。
1.2 调度算法
将栅栏分割,如图1所示,将栅栏均匀分割为α条子栅栏。同一时刻只有唯一子栅栏处于工作状态,其他处于休眠状态。
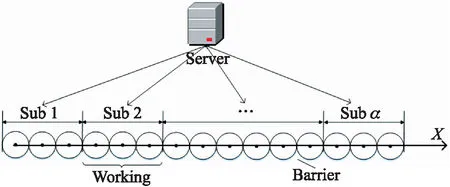
图1 栅栏分割图
激活Sub1子栅栏,运行t时间后进入休眠状态,当Sub1进入休眠状态后,激活Sub2,同样运行时间t后进入休眠状态,然后按顺序轮流调度,直到所有子栅栏都激活工作一次,完成一次栅栏调度。最后按照上述方法开始新一轮的栅栏调度,直到所有子栅栏能量耗尽。
t=T/β
(1)
式中:中:β为常数,T为节点总共运行的时间,当完成β次调度后节点能量刚好耗尽。
L表示栅栏长度,将其均分为α段,每段长度为L/α,以其最左端传感器节点为原点,建立一维坐标系,如图1,根据分割子栅栏的数量、横坐标和栅栏的长度,给传感器节点分配其所属的子栅栏编号(S1,S2,…,Sα)。由服务器控制子栅栏的循环激活调度,并且发送激活或休眠命令,进而控制其工作状态。
2 1-barrier 分析
本节分析栅栏在1-barrier流水式调度算法下的生存时间和检测率。在3.1节中计算入侵者的平均通过时间。应用平均通过时间计算出3.2节中的总体的检测率。再计算出3.3节栅栏能延长的生存时间。
2.1 最短感知距离与平均通过时间
设入侵者通过感知区域的速度为v,且角度θ和位置x都为随机。如图2,传感器节点位于0处。图中d(θ,x)表示入侵者通过感知区域时的最短感知距离,le(θ,x)表示节点感知范围内通过路径的长度。
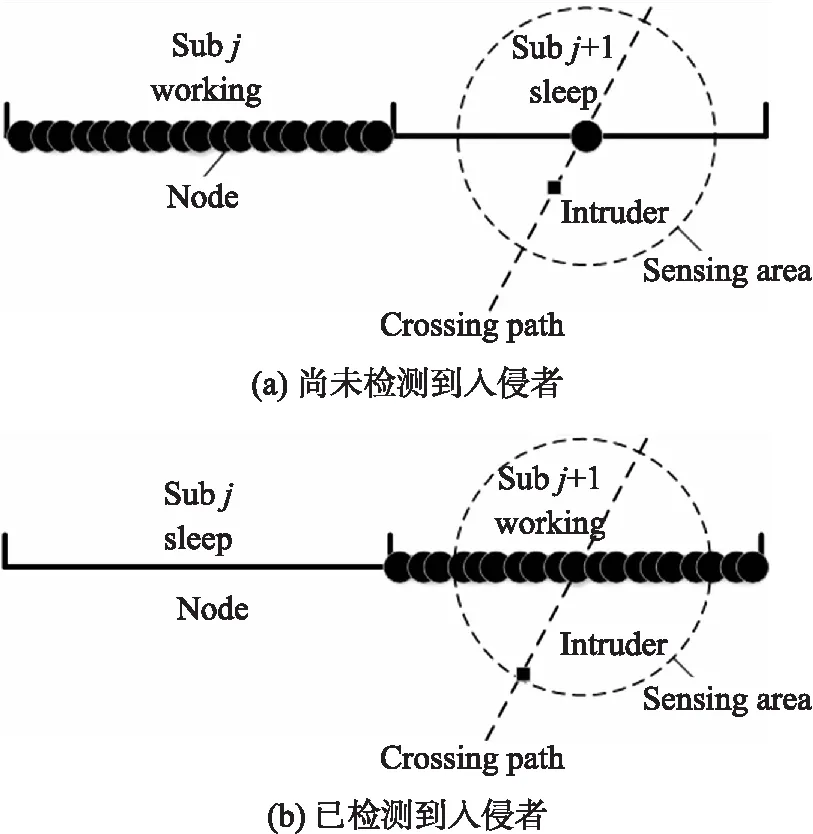
图2 通过路径图
由于θ∈[0,π]和x∈[-R,R]是相互独立的随机变量,且等概率,因此x的概率密度函数f(x)如式(2)所示,θ的概率密度函数g(θ)如式(3)所示。
(2)
式中:中:R表示节点感知半径。
(3)
最短感知距离如式(4)所示。
d(θ,x)=|x|sinθ
(4)
式中:(4)中R为节点感知半径,0≤θ≤π,-R≤x≤R。
计算d(θ,x)的平均值davg,如式(5)所示,计算可得davg的值如式(6)所示。
(5)
(6)
平均通过路径长度如式(7)所示。
(7)
式中:R为节点感知半径,0≤θ≤π,-R≤x≤R。
计算le(θ,x)的平均值leavg,如式(8)所示,通过泰勒级数可求得leavg的近似值如式(9)所示。
(8)
(9)
式中:R表示节点感知半径。
通过leavg可计算入侵者的平均通过时间ct,如式(10)所示。
(10)
2.2 栅栏平均检测率
文中研究栅栏在概率感知模型下的检测率,概率感知模型如式(11)所示。
(11)
式中:d(i,j)为节点i与入侵者j之间的距离,m是个可调的参数。
入侵者被栅栏检测到可分为二种情况:①在未被激活的栅栏处试图通过,但子栅栏在其通过感知范围前被激活了。②直接被处于工作状态的子栅栏检测到。第1种情况如图3所示。图3(a)表示入侵者尚未被检测到,图3(b)表示入侵者被检测到。

图3 栅栏检测图
第1种情况的栅栏检测率p1如式(12)所示。
(12)
式中:α表示子栅栏的数量,davg如式(6)所示。
第2种情况的栅栏检测率p2如式(13)所示。
(13)
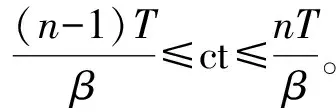
综上所述,p1、p2之和即为整条栅栏的平均检测率P,如式(14)。
(14)

从式(14)可以看出当α值越小时,表示子栅栏的数量越少,其长度则越长,对应检测率越大。β越大时,T/β越小,表示子栅栏状态切换的越快,因此能监测到入侵者的概率越大。
2.3 栅栏生存时间
如不分割子栅栏,而是直接激活栅栏中所有节点,则栅栏的生存时间为T。分割时,当消耗完所有子栅栏的能量后,认为该栅栏死亡。单个子栅栏激活状态的时间为T/β,则所有子栅栏都激活工作一次需要时间为αT/β,栅栏的生存时间为αT。所以文中调度方法使得栅栏的生存时间延长了(α-1)T。
3 k-barrier分析
设在栅栏部署区域内存在k条栅栏,k条栅栏同时进行独立的流水式栅栏调度。则入侵者通过k条栅栏的检测率Pk如式(11)所示。
Pk=1-(1-P)k
(15)
式中:P表示一条栅栏在流水式调度算法下的检测率,可由2.2节计算得到。
在保证k条栅栏检测到入侵者的概率不小于Pth时,Pk≥Pth,则每条栅栏的检测率P如式(16)所示。
(16)
同时调度k条栅栏时,若使用流水式调度算法,则k条栅栏的生存时间为αT。而按照传统的栅栏调度方法,栅栏总共能生存的时间为kT。因此流水式调度算法比传统的方法能延长k-栅栏的生存时间为(α-k)T。
4 仿真实验
实验中栅栏长度L=1 000 m,总共有k=4条栅栏。传感器节点的最大生存时间t=24×60×60×7 s(一周),节点概率感知模型中m=0.07。实验结果为200次实验的平均结果,检测率为4条栅栏总共的检测率。
4.1 入侵轨迹平均长度
本次实验验证入侵者以某个节点为圆心,通过其感知区域的平均通过路径长度leavg。实验中入侵者以任意角度θ∈(0,π)通过一条栅栏,实验结果如图4所示。横坐标表示传感器节点感知半径,纵坐标表示平均通过长度leavg。
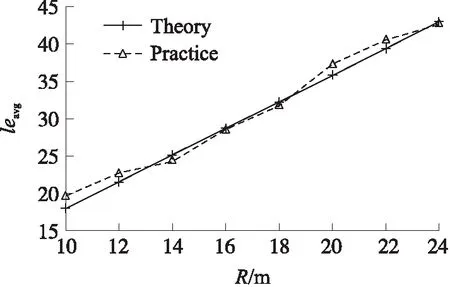
图4 通过路径长度图
实验结果表明随着感知半径R的增大,平均通过路径长度leavg呈线性增长,且文中2.1节计算的通过路径平均长度与实验结果符合。因为传感器节点的感知半径R增加,其感知范围也增加,因此入侵者在传感器节点感知范围内的通过路径也会相应的增加。
4.2 α、β对检测率的影响
本次实验n=4,节点感知半径R=20 m,入侵者速度为1 m/s。T/β表示子栅栏处于激活状态的时间。α表示子栅栏的数量,α越小子栅栏越少,每条长度越长。α、β的取值在定义域(2.2节)内。本次实验为采用流水式调度算法的4条栅栏同时对入侵者的检测率,结果如图5所示,横坐标为α,纵坐标为检测率Pk。

图5 检测率图
实验结果表明β越大,对入侵者的检测率越高,这是由于当β增大时,T/β减小,子栅栏处于激活状态的时间就缩短,对应的状态切换速度加快,检测到入侵者的概率也就增大。与此同时,当α增大,检测率减小,这是由于α增大,子栅栏的长度缩短,导致栅栏的检测率减小。当α=7时,实验中β的两种取值都保证了栅栏对入侵者的检测率大于90%。同时通过实验验证了文中的理论推导。
4.3 通过速度对检测率影响
理论上入侵者的通过速度越快,栅栏检测到的概率越低。本次实验中α=4,节点感知半径R=20 m,入侵者通过速度为1 m/s~7 m/s,以1 m/s递增,实验结果如图6所示,横坐标表示通过速度,纵坐标表示检测率。
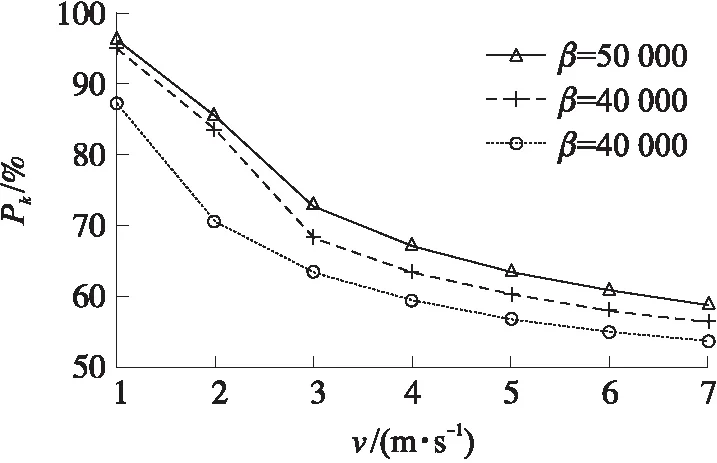
图6 通过速度影响图
从实验结果可以发现,检测率随着通过速度增加而减小,且随着β增大而增大,这是由于β增大,子栅栏处于激活的时间会缩短,子栅栏调度的速度加快,在入侵者通过速度一定的情况下检测率更高。
4.4 栅栏生存时间
通过实验,使用流水式栅栏调度算法(FSA)和传统调度方法,验证了条件当检测率在85%以上的时候,栅栏生存时间的差异。实验中β=33 833,k=4,节点感知半径R=20m,入侵者速度为1 m/s。结合4.2节的实验,检测率大于90%时α的取值分别为4、5、6、7、8、9、10。实验结果如图7所示,横坐标为α,纵坐标为栅栏生存时间。
实验显示,在保证检测率大于90%的同时,栅栏的生存时间随着α增大而变长。且生存时间远远超过传统的栅栏调度算法,为α/4倍。
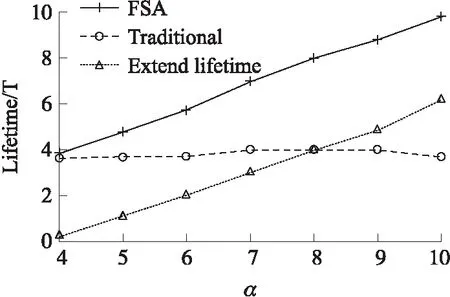
图7 栅栏生存时间图
5 总结
本文提出了流水式栅栏调度算法(FSA),对延长栅栏生存时间非常有效。该算法通过将子栅栏轮流激活来增长子栅栏的生存时间,并且保证了一定的检测率。除了满足这两项基本需求外,本算法并不是直接把所有栅栏同时激活,而是实施了栅栏内部的子栅栏调度,从而延长栅栏的生存时间。后续工作将进一步研究在确保检测率的情况下延长栅栏的生存时间。
