基于文丘里的湿气流量测量实验研究
2019-05-08
(中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,成都 610041)
0 引言
湿气作为一种特殊的气液两相流广泛存在于注汽采油、天然气开采和运输、火力发电和核电汽轮机中。从气田开采出的天然大多都会携带少量水或液态烃而变成湿天然气[1]。即使经过气液分离的干天然气,在运输过程,受温度和压力的变化,会凝析出液态碳水化合物,并输送距离逐渐增多,最终形成湿天然气[2]。因此湿气流量的在线测量既可以降低油气田投资和运营成本,也为简化生产工艺和提高气藏和气井的综合管理水平提供科学依据。随着第四次工业革命的迅速推进,物联网将会得到迅速发展,如果能对每口井的产量和每根支线的气量有精确采集,并根据市场的需求去控制油气的产量,能给城市智慧化提供更有利的支撑。
文丘里已成为一种最常用的湿气流量计,因为它结构简单,测量重复性好且造价低廉。国内外很多商用湿气和多相流量计都采用它进行流量测量[3]。
根据等同翻译ISO/TR 11583[4]的GB/Z 35588[5],对于气相体积比大于95%的气液两相流被认为湿气。标准还给出针对文丘里和孔板测量湿气的指导性修正模型,但ISO/TR 12748[6]给出的文丘里测量湿气指导性修正模型就与ISO/TR 11583不同。GB/T 35065.1[7]也给出了湿天然气的流量修正模型但与前几个标准都不相同。因此用文丘里测量湿气的修正模型仍需进一步研究。
当前国内外学者也提出各种虚高模型,但这些模型都是针对工业湿气测量而提出来的,这些流量计的入口直径都在2~48 in范围[8]。但几乎未见到针对民用的小口径湿天然气流量虚高研究报道。Britton等人[9]在研究文丘里测量湿气时发现,在湿气参数不变,流经入口直径不同,其他参数相同的两个文丘里时,入口直径越小的虚高越小。因此,本文将采用入口直径为6 mm的小文丘里开展氮气和水湿气流量虚高测量研究。
1 实验系统及测量原理
1.1 实验回路
如图1所示,实验回路由水箱、柱塞泵、缓冲罐、流量计、混合器、阀门、氮气瓶以及相应管道等设备构成。实验回路设计压力为4 MPa,实验液相支路流量为100 kg/h,气相支路流量为50 kg/h。
实验回路如下:水作为液相工质,从水箱经柱塞泵注入液相缓冲罐后,再由被阀门PV1减压的氮气压入混合器中,这个过程中还有多个阀门对其进行参数调节。氮气作为气相工质,从多个氮气瓶经减压阀减压后汇入气相缓冲罐中,再经阀门调节后进入混合器。调节好参数的氮气在气流式雾化器中把水雾化成湿气后流入文丘里中进行气液两相流流量测量。
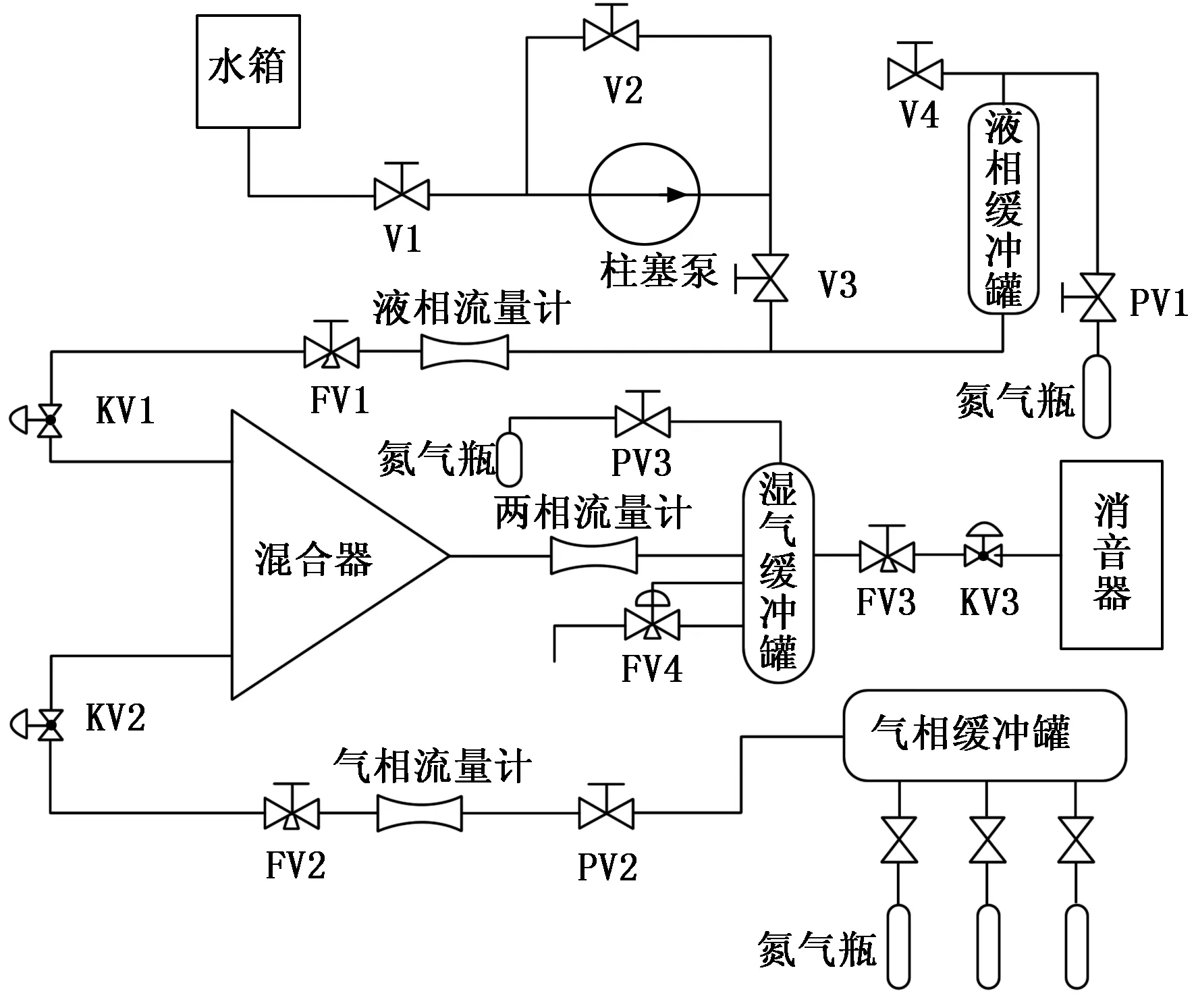
图1 实验回路流程示意图
阀门FV1用于调节实验液相支路的水流量,阀门FV2用于调节实验气相支路的氮气流量,阀门FV3辅助FV1和FV2调节湿气支路流量。阀门PV1用于调节液相支路压力,阀门PV2用于调节气相支路压力,阀门PV3用于实验湿气支路的压力。安装在湿气缓冲罐中心的液位开关与FV4阀门关联,当液位开关闭合时,测控系统自动打开阀门,并延时一段时间后关闭。
实验回路中,阀门PV1、PV2和PV3为减压阀;阀门FV1、FV2、FV3和FV4为调节阀;阀门KV1、KV2和KV3为球阀;阀门V1、V2、V3和V4为截止阀。
为了避免部分实验工况压力出现中出波动或不稳定现象,在实验的每个支路都安装一个缓冲罐。
实验的参数范围:压力0.5~2.0 MPa;液相支路流量0~100 kg/h,气相支路流量0.5~40 kg/h,干度0.2~1.0,气体密度弗鲁德系数1.0~8.5,洛克哈特-马蒂内利参数0~0.34,气相体积比95%~100%。
1.2 实验测量系统
实验系统的流量测点共有3个,其中液相流量Wl和气相流量Wg均采用E+H的83A02质量流量计,其液相测量精度为0.1级,气相测量精度为0.5级,流量测量范围0~100 kg/h。用于湿气流量Wm,g测量的文丘里管参数为:入口直径6 mm,直径比0.567,入口收缩段夹角21°,出口扩散段夹角12°。实验系统的其他测点有:文丘里入口和气相缓冲罐上压力测点、文丘里出口温度测点、文丘里差压测点、液相缓冲罐液位测点和湿气缓冲罐液位开关测点。在柱塞泵出口和液相缓冲罐还安装了现场压力表。压力采用Rosemount的0.05级3051S1CG3A压力变送器进行测量,温度采用Omega的A级Pt100进行测量,差压和液位均采用Rosemount的0.05级3051S1CD3A差压变送器进行测量,液位开关采用Omega的侧装LVN-93型浮球开关。
1.3 湿气测量原理
1.3.1 文丘里测量原理
根据伯努利定律和连续性方程可建立起单相流体流过节流件(文丘里管)的质量流量与其压降的关系式[10]:
(1)
(2)
其中:W为质量流量(kg/s);Cd为文丘里管的流出系数;ε为流体可膨胀系数;d为喉部直径(m);ΔP为文丘里管差压(Pa);ρ为流体密度(kg/m3);β为喉部直径d与入口直径D的比,即直径比;Red为喉部雷诺数;μ,流体的动力粘度(Pa·s)。GB2624.1认为流出系数只与雷诺数有关,且机械加工的文丘里系数与喉部雷诺数具有更好的相关性[10],即可认为:
Cd=f(Red)
(3)
1.3.1 湿气的相关参数
1.3.1.1 洛克哈特-马蒂内利参数
Lockhart 和Martinelli把等量的液相、气相单独流过节流件时,差压比值的平方根定义为洛克哈特-马蒂内利参数(简称L-M参数)[11]:
(4)
其中:ΔPl、ΔPg分别为等量的液相、气相单独流过节流件时的差压(Pa);ρg和ρl分别为气相和液相的密度(kg/m3);DR为气液两相密度比;Wl和Wg分别为液相和气相的真实质量流量(kg/s)。
1.3.1.2 虚高修正系数
参考GB/Z 35588,虚高修正系数Φ可表示为[5]:
(5)
其中:Wm,g为气相的测量(虚高)质量流量(kg/s);ΔPtp为文丘里测量差压(Pa)。
1.3.1.3 气体密度弗鲁德系数
W.Froude为表示重力对流动影响的准数,提出了弗鲁德系数,而气体密度弗鲁德系数(简称气相弗鲁德数)[11]可以表示为:
(6)
其中:υsg是气相表观速度(m/s);g为重力加速度(m/s2);D为入口直径(m)。
1.3.1.4 韦伯数
韦伯数是表示惯性力和表面张力效应之比,而湿气的韦伯数[11]可表示为:
(7)
其中:σl为液相表面张力(N/m)。
1.3.1.5 液气体积比
把液相体积流量与气相体积流量比值定义为液气体积比:
(8)
其中:Ql和Qg分别为液相和气相体积流量(m3/h)。
1.3.2 湿气虚高模型
对于满管稳定流动且质量流速不随时间变化的流体,其动量方程[12]可以表示为:
(9)
其中:τ0为流体与单位长度管壁的切应力(N/m);L为边界长度(m);α为截面含气率;χ为质量含气率;ρtp为气液两相混合物密度(kg/m3);A为截面积(m2);θ为流动方向与水平线的夹角(°)。
流体在水平安装的文丘里中流动时,其压力损失主要来自与管道摩擦产生的摩擦压降和沿流动方向的流通截面积变化产生的加速压降。由于文丘里较短,所以摩擦压降相比加速压降可以忽略不计。
从而对式(9)简化后可以得到流体在文丘里中的加速度压降:
(10)
忽略气液两相流体流经文丘里时的密度变化,假定在整个流通截面上压力均匀分布,即可以用文丘里测量差压替代实际差压。同时假定气液两相间滑速比和截面含气率都保持不变,对式(10)沿文丘里管入口截面到喉部截面进行面积积分,可以得到:
(11)
其中:A1为入口段截面积,m2;A0为喉部段截面积,m2。
根据式(10),当气相单独流过文丘里时,其差压可以表示为:
(12)
由式(10)、(11)和(5)可得虚高修正系数与质量含气率、气液密度比、截面含气率及L-M参数的关系式:
(13)
再结合截面含气率α、质量含气率χ、滑速比s[13]的关系式:
(14)
将式(14)代入式(13)得:
(15)
(16)
(17)
式(17)就是湿气的虚高模型,根据GB/Z 35588,模型中Chisholm系数CCh可以表示为:
(18)
标准认为虚高指数n是一个与气相弗鲁德数、液相物性和直径比有关的参数。
结合式(1)和(5)可以获得气相的真实质量流量修正模型:
(19)
结合式(4)、(5)和(17),可以把Chisholm系数表示为:
(20)
通过对式(18)进行变换,可以把虚高指数表示为:
(21)
1.3.3 虚高指数经验关系式
1.3.3.1 Chisholm孔板虚高指数
在1977年,Chisholm[14]基于均相流密度模型,推到出滑速比s=(ρl/ρg)0.25,入式(16)可得:
(22)
因此,Chisholm孔板经验关系式为:
n=0.25
(23)
结合(22)和(17)可以获得Chisholm的虚高模型,在2018年该模型被GB/T 35065.1[7]采纳作为测量湿天然气流量的指导性修正模型。
1.3.3.2 De Leeuw文丘里虚高指数
在1997年,De Leeuw对入口直径4 in,直径比0.4的文丘里管进行湿气测量虚高研究,发现虚高指数与气相弗鲁德数有关,通过实验数据拟合,获得经验[15]关系式:
(24)
1.3.3.3 R-H文丘里虚高指数
在2009年,Reader-Harris等人对入口直径4 in直径比0.4、0.6和0.75,以及对入口直径6 in直径比0.55的水平安装文丘里管进行了大量的湿气测量虚高研究,发现指数与气相弗鲁德数、直径比和液体类型有关,获得经验[16]关系式:
n=max(a1+a2β2+a3ea4Frg/H,a5+a6β2)
(25)
其中:a1=0.583,a2=-0.18,a3=-0.57,a4=-0.8,a5=0.392,a6=-0.18。H是一个与液相表面张力有关的的系数,对于液态烃H=1,对于常温水H=1.35,对于饱和湿蒸汽H=0.79。
结合(25)、(18)和(17)可以获得R-H的虚高模型,在2012年该模型被ISO采纳作为文丘里测量湿气流量的指导性修正模型[4]。
1.3.3.4 Steven孔板虚高指数
在2009年,Steven R.等人通过对近几年的大量水平安装孔板湿气测量数据进行整理获得经验[17]关系式:
(26)
结合(26)、(18)和(17)可以获得Steven的孔板虚高模型,在2012年该模型被ISO采纳作为孔板测量湿气流量的指导性修正模型[4]。
1.3.3.5 Steven V锥虚高指数
在2009年,Steven R.等人通过对近几年的大量水平安装V锥,液相介质含水的湿气测量数据进行整理,获得经验[18]关系式:
(27)
1.3.3.6 徐式长喉文丘里虚高指数
在2012年,徐立军等对垂直安装,入口直径50 mm,直径比0.45的长喉文丘里进行湿气测量虚高研究,发现指数与气相弗鲁德数和气液密度比有关,其经验[19]关系式为:
(28)
其中:b1=0.47359213,b2=1.9897702,b3=1.8384189,b4=0.087328207,b5=7.4636959。
1.3.3.7 Graham文丘里虚高指数
在2014年,Emmelyn Graham等对垂直安装,入口直径4 in,直径比0.6的文丘里进行湿气测量虚高研究,发现指数可以直接用气液密度比表示,其经验[3]关系式为:
(29)
2 实验及结果分析
2.1 实验工况
由上所述,虚高修正系数主要跟气液密度比、气相弗鲁德数和L-M参数有关。从De Leeuw文丘里和Steven孔板虚高指数经验关系式,可以发现,气相弗鲁德数在1.5附近关系式有拐点。在2012年,Steven等人[20]对湿气进行可视化实验时发现,虚高指数经验关系式的拐点正好对应湿气流型从层状流转变为环雾状流。因此实验工况中气相弗鲁德数在1~2.5每隔0.5有一个气相弗鲁德数点,并在每个气相弗鲁德数点下完成多个L-M参数点,实验的主要工况参数如表1所示。
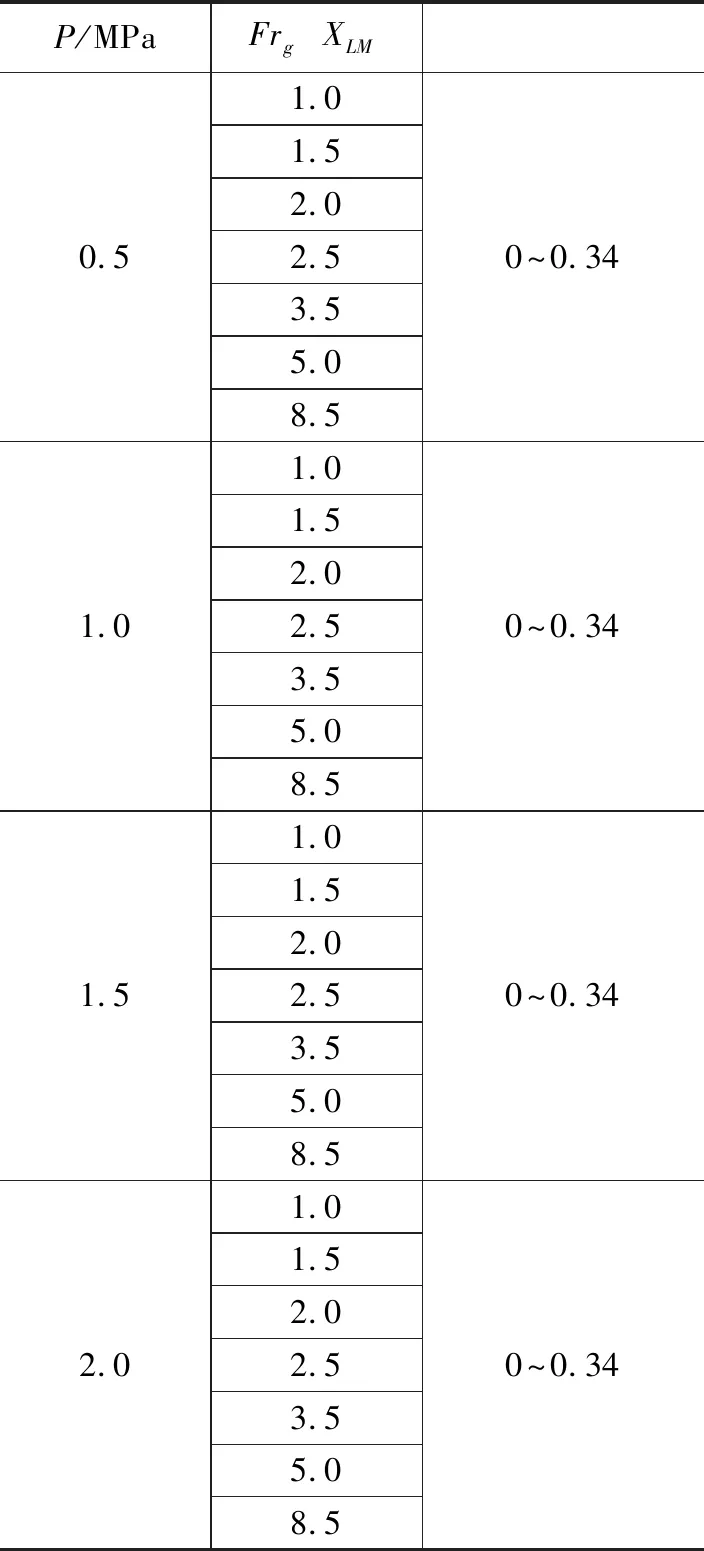
表1 实验工况分布表
2.2 实验方法和步骤
实验的氮气是从20 MPa高压氮气瓶经中减压进入实验回路。因此实验优先完成高压力工况。液相流量是通过氮气把液相缓冲罐内水压入混合器,因此优先完成低液相流量工况。实验中如果液相流量、气相流量或湿气压力不满足工况参数时,应先调节气相流量,再调压力最后再调液相流量。
实验步骤:先关闭阀门KV1、KV2、PV1、PV2和PV3,打开阀门V1、V2、V3和V4给液相缓冲罐补水直到阀门V4处溢流,停柱塞泵,关阀门V3和V4。打开气相缓冲罐接入的多个氮气瓶出口减压阀,使得气相缓冲罐内压力比实验工况压力高1.5 MPa左右,打开阀门KV2,调节阀门PV2控制气相支路压力比实验工况压力高0.5 MPa左右,调节阀门FV2和FV3使氮气流量比工况参数高1%左右。调节阀门PV3使得文丘里入口压力达到工况参数。打开阀门KV1,调节阀门PV1和FV1使水流量达到工况参数,适当调整阀门FV2和FV3使氮气流量达到工况参数。稳定1分钟后,开始采集一组数据,然后开始下一组工况。
实验中,如果液相缓冲罐内液位低于100 mm时,测控系统自动提醒。完成当前工况后,关闭阀门KV1、KV2、KV3和PV1。打开阀门V4释放液相缓冲罐内的氮气,打开阀门V3后,开启柱塞泵给液相缓冲罐补水,直到阀门V4处溢流,停柱塞泵,关阀门V3和V4。如果气相缓冲罐上压力低于2.0MPa时,测控系统自动提醒。完成当前工况后,关闭阀门KV1、KV2和KV3,更换所有连接气相缓冲罐的氮气瓶。
2.3 文丘里流出系数标定
实验中每做一个不同压力下的气相弗鲁德数工况点时都进行一次纯氮气实验。通过质量流量计的流量和文丘里入口压力来标定文丘里的流出系数,文丘里流出系数和喉部雷诺数关系如图2所示。从图中曲线可得到喉部雷诺数与流出系数的关系式。
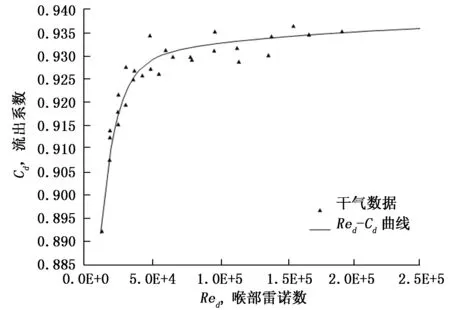
图2 流出系数和喉部雷诺数关系图
2.4 影响虚高的因素
2.4.1 L-M参数
从图3实验的虚高修正系数数据与L-M参数的分布关系图可以看出,随着L-M参数的增大,虚高修正系数增大,并且系数分布越离散。由此可见,影响虚高的因素不仅仅只有L-M参数。
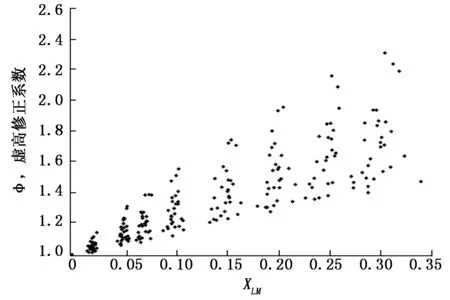
图3 虚高修正系数与L-M参数分布图
L-M参数是表示液相质量影响的重要指标,随着L-M参数的增加,液相对气相的阻塞就会越明显,气相对液相加速会造成更多的能量损失,从而造成更大的流量虚高。因此,L-M参数的变化与虚高修正系数呈递增关系。
2.4.2 气液密度比
从式(18) Chisholm系数可以看出,气液密度比是影响虚高的一个重要参数,同时L-M参数中也包含气液密度比,并且部分学者[3]认为气液密度比还是虚高指数的重要影响参数。
图4和图5分别是气相弗鲁德数为1.0和8.5时不同气液密度比下虚高修正系数的分布图。从图中可以看出气液密度比在相近的L-M参数下,随着气液密度比的增加,虚高修正系数变小。比较图4和图5可以发现,随着气相弗鲁德数的增大,气液密度比对虚高的影响越明显。
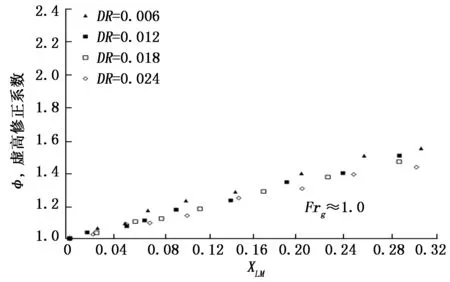
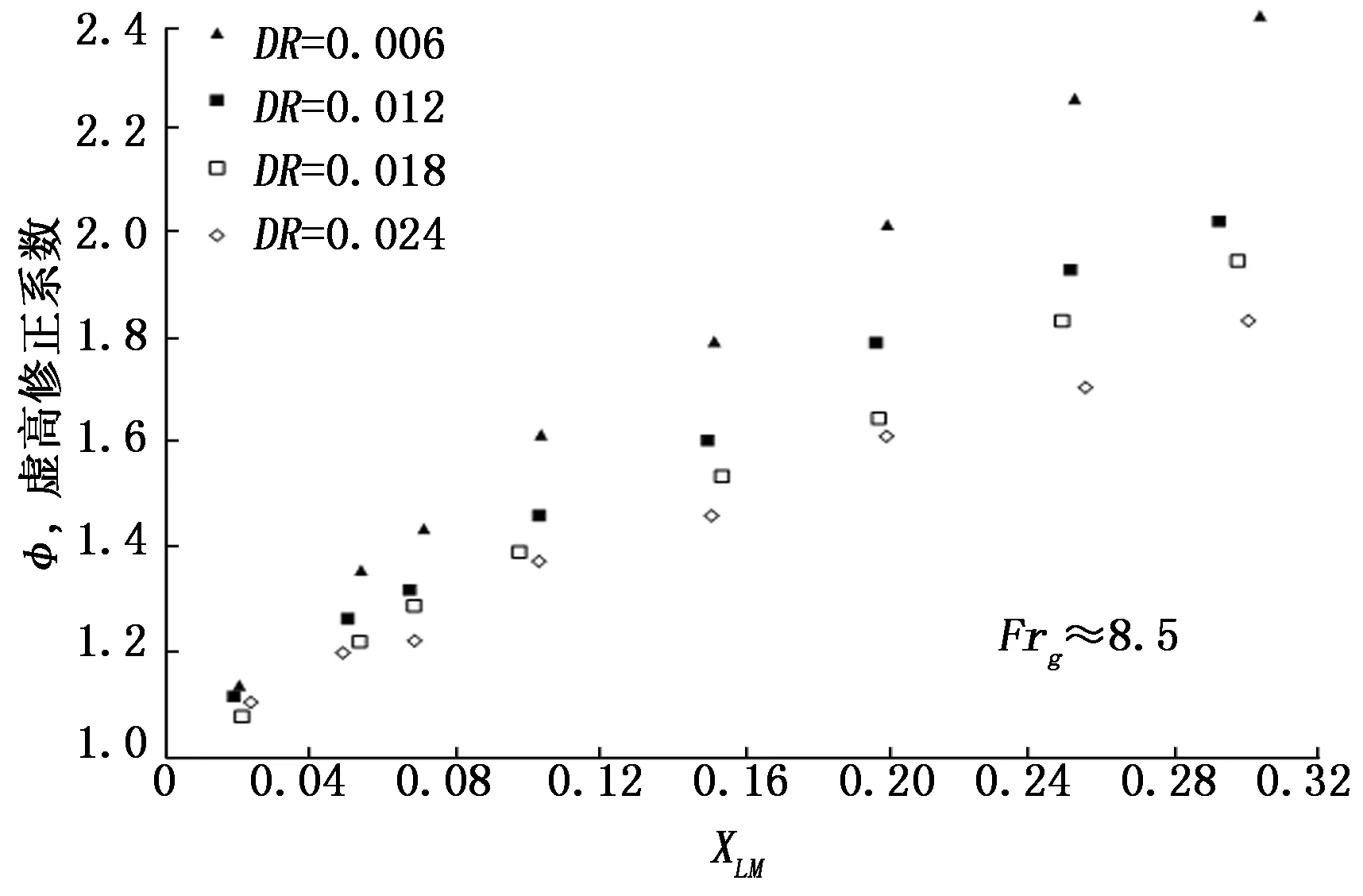
图5 Frg≈8.5,不同密度比下虚高修正系数分布图
图4Frg≈1.0,不同密度比下虚高修正系数分布图
对于常温下氮气水湿气的气液密度比是压力的函数,当压力上升时,气液密度比增大。由于水的可压缩性相比氮气来说很小,当压力上升时,水密度增加很小。这时,氮气单位体积内的质量上升,氮气驱动水需要的能量就会下降,从而虚高修正系数减小。
Steven[21]用入口直径4英寸,直径比0.401的文丘里在CEESI实验平台对DR为0.013、0.052和0.088的天然气和癸烷湿气进行研究,也给出了类似的结论。Steven等人[22]用入口直径4英寸,直径比0.66的孔板在CEESI实验平台对DR为0.024和0.089的湿天然气进行研究,也给出了类似的结论。同时,他们对入口直径为8英寸的四声道超声波流量计在DR为0.017、0.035和0.074的湿天然气进行研究,也给出了类似的结论。
2.4.3 气相弗鲁德数
图6和图7对比了气相弗鲁德数在1.0、1.5、2.0、3.0、5.0、7.0和8.5下,不同密度下的虚高修正系数分布。从图可以看出,接近的L-M参数下,气相弗鲁德数减小,虚高修正系数降低,且密度比越低气相弗鲁德数对虚高影响越明显。
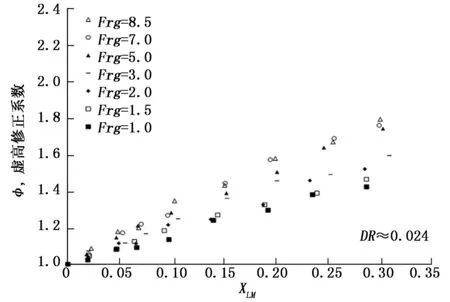
图6 DR=0.024,不同Frg下虚高修正系数分布图
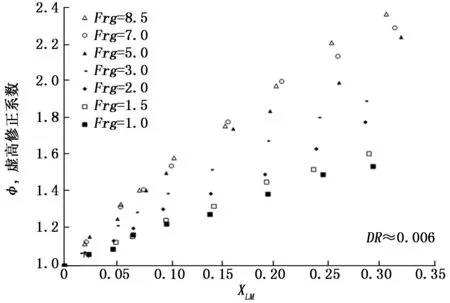
图7 DR=0.006,不同Frg下虚高修正系数分布图
由于气相弗鲁德数Frg=f(υsg,ρg,ρl),当气液密度不变时,气相弗鲁德数减小相当于气相表关速度降低,这样气相对液相的摩擦力减小,液相对气相的阻碍变小,从而两相间的动量交换损失会随着流速的降低而减小,因此气相弗鲁德数变化与虚高修正系数呈递增关系。
STEWART等人[23]分别用入口直径4英寸,直径比为0.4、0.6和0.75的文丘里管在NEL实验平台对气相弗鲁德数0.5~3.5(直径比为0.4)和1.5~5.5(直径比为0.6和0.75)的氮气和Exxsol D80湿气进行研究,也给出了类似的结论。Steven等人[24]入口直径8英寸,直径比为0.6的文丘里管在CEESI实验平台对气相弗鲁德数为1.50、2.65和3.63的天然气和Exxsol D80湿气进行研究,也给出了类似的结论。
2.4.4 韦伯数对虚高修正系数影响
图8和图9对比了韦伯数在4.6、10、18和41下,不同密度比下的虚高修正系数分布。从图可以看出,接近的L-M参数下,韦伯数增大,虚高修正系数上升,且密度比越低韦伯数对虚高影响越明显。
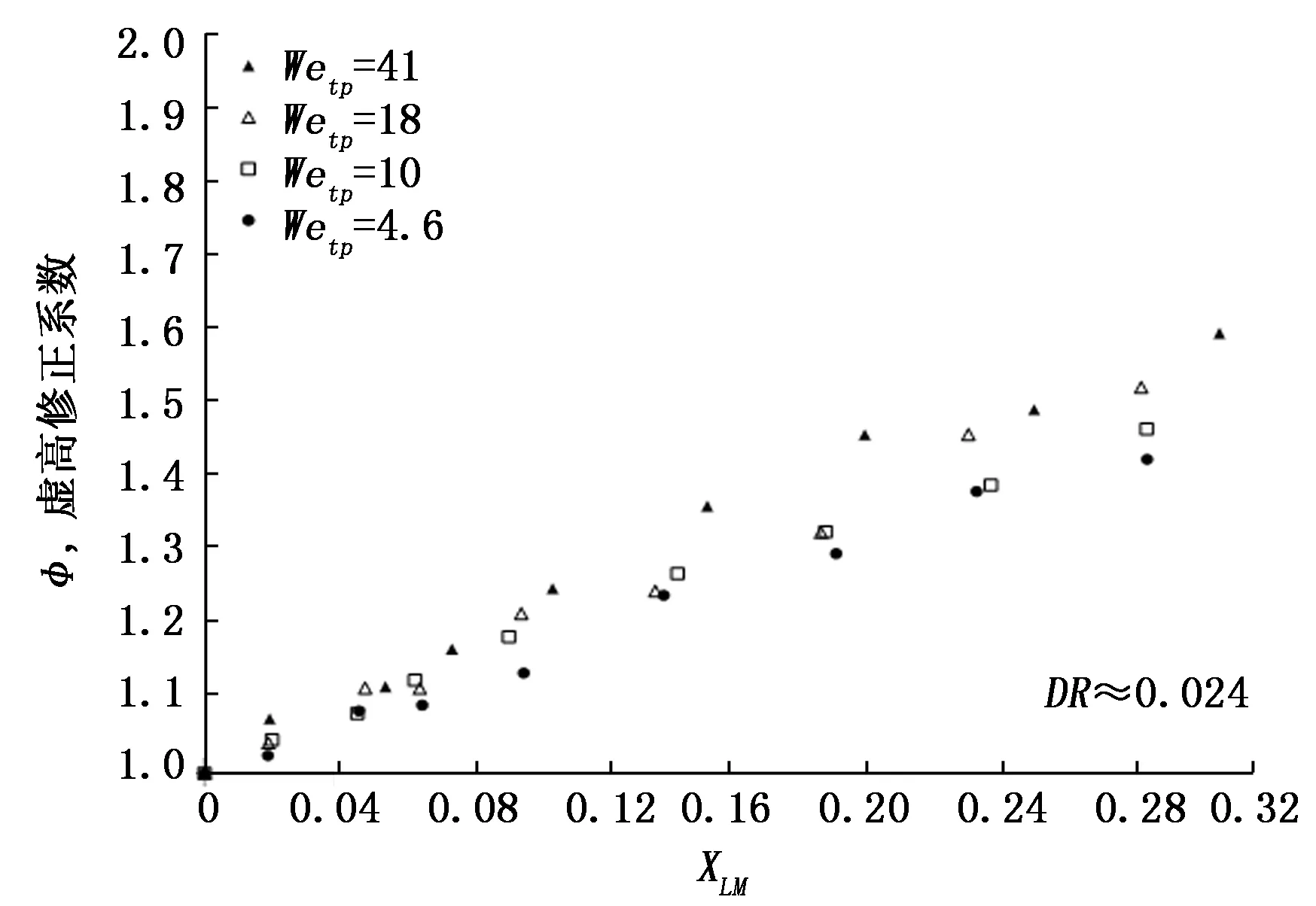
图8 DR=0.024,不同Wetp下虚高修正系数分布图
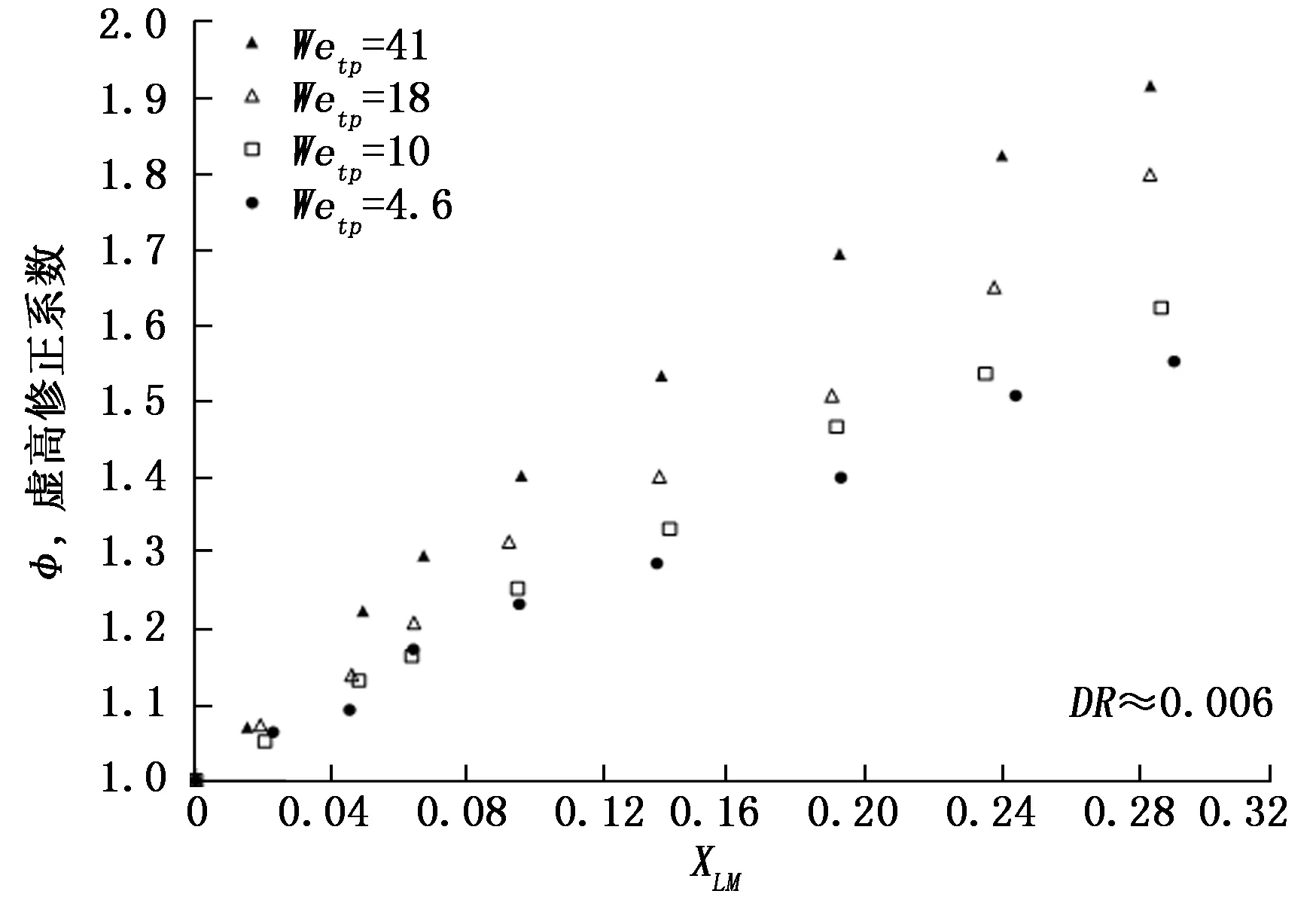
图9 DR=0.006,不同Wetp下虚高修正系数分布图
由于韦伯数Wetp=f(υsg,ρg,σl),当压力变化很小时,气相密度和表面张力变化很小,韦伯数的变化就相当于气相表关速度的变化,因此,韦伯数的对虚高修改系数的影响与气相弗鲁德数相似。
2.4.5 液气体积比对虚高修正系数影响
从图10和图11可以看出,液气体积比的变化与虚高修正系数呈递增关系。对比图4和图10,以及图5和图11,在气液密度比和气相弗鲁德数均相同下,液气体积比与虚高修正系数的斜率大于L-M参数与虚高修正系数的斜率。并且在气液密度比减小或气相弗鲁德数增加时表现越明显。
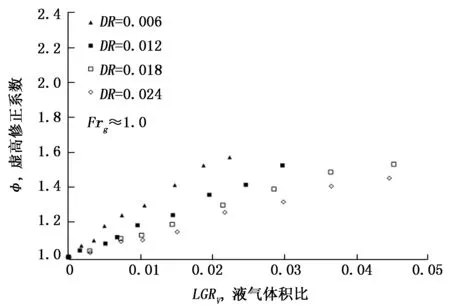
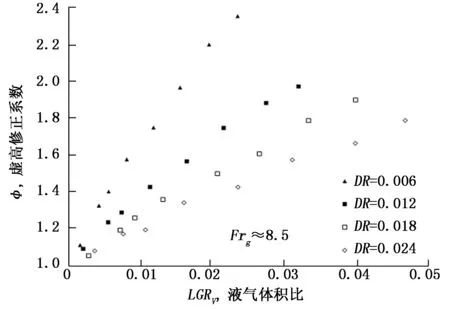
图11 Frg≈8.5,不同密度比下虚高修正系数与液气体积比的分布图
图10Frg≈1.0,不同密度比下虚高修正系数与液气体积比的分布图
液气体积比即液相相对于气相的体积比例,液气体积的增加就会使液相对气相的阻塞越明显,因此,其作用与L-M参数相似。
3 实验数据处理
3.1 改进的指数关系式和修正模型
把实验数据按式(4)~(6)、(20)和(21)进行计算,可以获得气相弗鲁德数和虚高指数的分布。本文参考R-H文丘里虚高指数修正关系式对两者进行了非线性规划求解,获得了改进的虚高指数经验关系式:
(30)
结合式(1)、(5)、(17)、(18)和(25),可以获得适合于小口径文丘里测量湿气的气相流量修正模型:
(31)
3.2 虚高指数比较
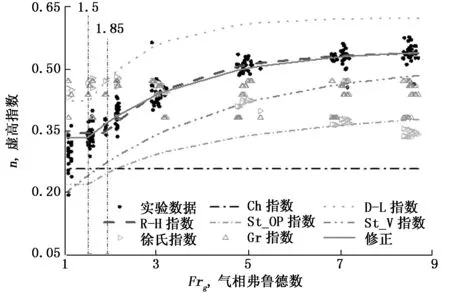
图12 预测虚高指数与实验数据对比
把实验数据代入式(23)~(30)这8个虚高指数经验关系式,就可获得不同关系式预测的虚高指数与气相弗鲁德数分布。图12为预测虚高指数与实验数据对比图。从图可以看出De Leeuw文丘里虚高指数、R-H文丘里虚高指数、Steven孔板虚高指数和Steven V锥虚高指数的分布与实验数据分布趋势相似,R-H虚高指数与改进虚高指数分布基本重合。但两者的拐点不同,其中R-H关系式拐点在Frg=1.85附近,改进关系式拐点在Frg=1.5附近,与De Leeuw文丘里和Steven孔板虚高指数经验关系式拐点一致。
3.3 误差分析
分别把8个虚高指数关系式代入式(16)和(19)可获得每个虚高模型下气相流量修正值,再与实验真实的气相流量进行误差比较。气相流量的相对误差ΔE和均方根误差δ计算方法如下:
(32)
(33)
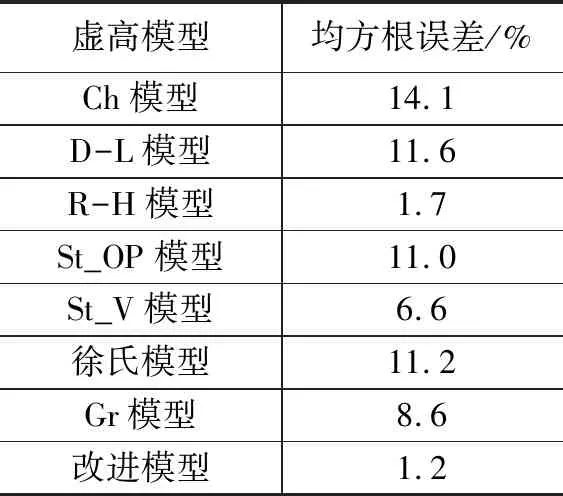
表2 不同虚高模型的气相流量均方根误差
图13和表2分别是8个不同虚高模型修正的气相流量与实验真实气相流量的相对误差和均方根误差比较图表,从图表可以看出R-H文丘里虚高模型、Steven V锥虚高模型和改进模型修正的气相流量相对误差和均方误差都比较小。其中,Steven V锥虚高模型95.1%的数据都落在[-11.5%,0%]相对误差带内,该模型的均方误差为6.6%。R-H虚高模型95.1%的数据都落在±3.2%相对误差带内,R-H虚高模型的均方误差为1.7%。改进虚高模型96.4%的数据都落在±2.1%相对误差带内,改进虚高模型的均方误差为1.2%。
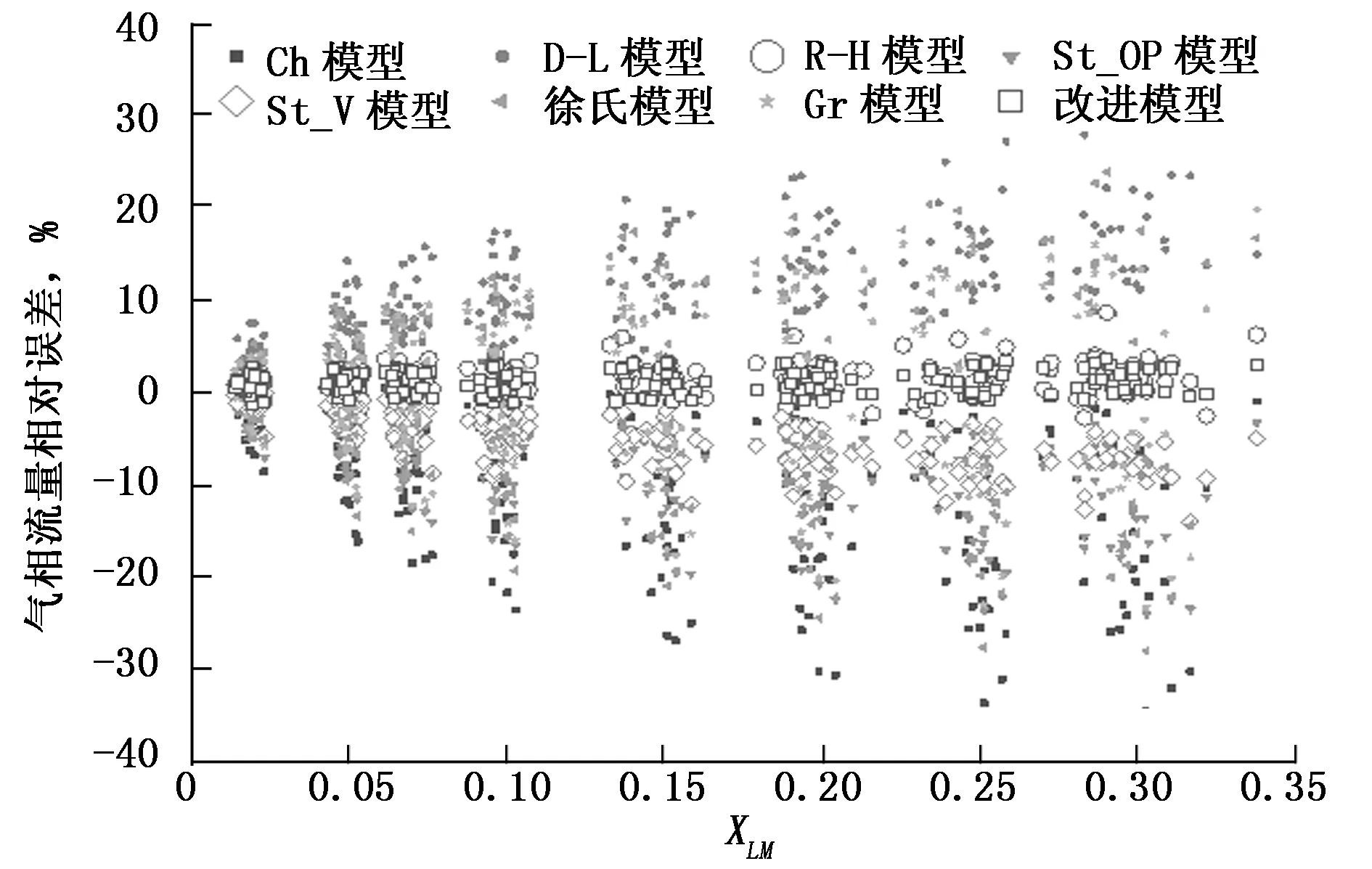
图13 不同虚高模型修正的气相流量相对误差分布
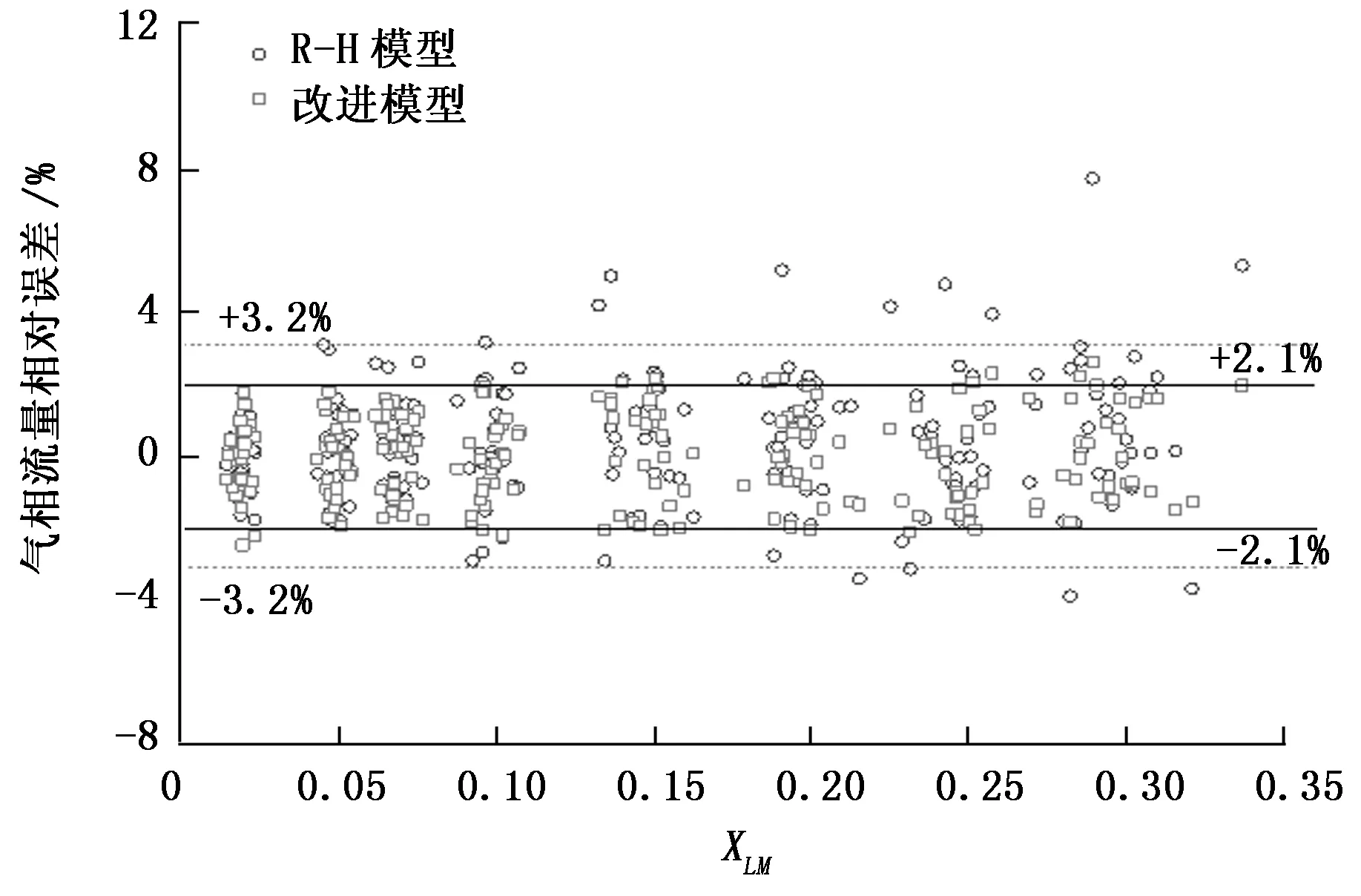
图14 R-H和改进虚高模型的气相流量相对误差比较
4 结论
本文采用一台入口直径6 mm,直径比0.567的文丘里对氮气水湿气进行了流量测量虚高实验研究,并获得如下结论:
1)实验研究了常温下氮气水湿气流经文丘里时的虚高特性,共获得224组实验数据。其中实验湿气的参数范围:压力0.5~2.0 MPa,气相弗鲁德数1.0~8.5,L-M参数0~0.34。
2)分析了L-M参数、气液密度比、气相弗鲁德数、韦伯数和液气体积比对湿气虚高修正系数的影响。其中L-M参数、气相弗鲁德数、韦伯数和液气体积比与虚高修正系数呈递增关系,气液密度比与虚高修正系数呈递减关系。
3)调研了基于差压流量计的典型虚高指数关系式,并根据实验数据改进了R-H关系式。改进的关系式与De Leeuw文丘里和Steven孔板关系式拐点一致。
4)对比了多个虚高模型修正的气相流量值与实验真实气相流量值的相对误差和均方根误差。发现R-H文丘里虚高模型和Steven V锥虚高模型误差较小。
5)改进的虚高模型修正的气相流量相对误差96.4%落在±2.1%误差带内,虚高修正系数的均方根误差为1.2%,优于其他模型的修正结果。
