考虑无人机杆塔巡视避障的两阶段路径优化
2019-05-08
(武汉大学 电气与自动化学院,武汉 430072)
0 引言
随着无人机在输电线路杆塔精细化巡视中的应用,为克服传统由作业人员将无人机带至待巡检杆塔放飞进行巡检存在的不足,提高巡检流程自动化程度,节省人力投入,全自动无人机巡视已成为该领域的发展重点。如何在巡检过程中,使续航里程固定的无人机在续航里程内尽可能多地巡视输电线路杆塔,优化杆塔巡视路径,提高巡视工作效率是值得研究的问题。
文献[1]提出了用遗传算法对于巡视路径中障碍规避的路径优化,文献[2]提出在三维平面建立柱状障碍空间,提出结合支持向量回归算法和A*算法原理的避障路径规划算法,但是无人机的全自动精细化巡视通常需要经过多个线路杆塔,在避障算法基础上还需要完善巡视路径的规划。对于无人机巡视杆塔的次序,文献[3]基于穷举法和人工比较研究了确定杆塔最优巡检路径的方法,但是该方法没有考虑无人机如何在巡视过程中避开杆塔间障碍的路径优化。文献[4-5]综述了无人机在输电线路巡检中的应用。文献[6]利用人工势场法提出了面向无人机巡视避障和扩大巡视面积的规划方法,但该方法需要无人机搭载雷达的应用场景,并且规划目标是巡视面积扩大,而不是巡视路径优化,与电力系统无人机的全自动精细化巡视需求还存在差异。文献[7-13]关注的是没有特定场景的无人机路径规划和协同任务问题,可以为无人机巡检杆塔路径规划提供启发。基于此,本文围绕无人机全自动精细化巡视输电线路的杆塔巡视路径和杆塔间避障路径的双重优化问题开展研究。
通过将无人机巡视杆塔的次序优化视为旅行商问题(TSP),利用地图上杆塔坐标位置,分别用动态规划算法和模拟退火算法优化经过不同拍摄点的次序,比较两种算法的效果。传统的求解TSP问题的方法是启发式算法(比如模拟退火算法),在本文中提出将确定性算法即动态规划算法引入无人机路径的规划之中,论证了动态规划算法相对于启发式算法的优越之处。对于巡视的杆塔间避障路径优化,通过使无人机与地面保持确定的相对高度,把地图上超过无人机飞行高度的物体作为障碍点标注,将三维路径规划转化为二维路径规划,并用人工势场法进行避障最优路径求解。在此基础上,基于两种路径优化的结合,提出了面向无人机全自动化精细化巡视输电线路杆塔的路径规划方法。最后,通过仿真验证了所提巡视路径规划算法的有效性。
1 无人机基于双调巡航线路的路径优化
无人机经过所有的拍摄点并回到起点,可以等价为旅行商问题(Traveling Salesman Problem, TSP),属于NP完全问题。由于该问题在多项式时间难以求得全局最优解,因此通常采用具有随机性的启发式算法求解。这种求解虽然存在通用性强,在多数情况下都能在有限时间内搜索得到巡航路线的较短路径的特点,但求解结果对启发式算法相关参数设置具有敏感性,并且求解TSP的时间复杂度较大。针对利用启发式算法求解无人机巡视路径TSP的不足,通过在无人机巡航路径中,增加要求无人机沿单方向离开,再沿单方向返回的约束,将原来路径优化的TSP转化为具有双调欧几里得特性的TSP,进而将包含大规模巡视杆塔的路径优化转化为多个仅包含两个巡视杆塔间最优路径优化的子问题,从而在利用动态规划法快速求解两个杆塔间的最优巡视路径的基础上,基于各子问题最优解构造初始优化问题的最优解。
用点集V={v1,v2,…,vn}表示无人机需要巡视的各杆塔,dij表示杆塔v1和v2间的距离。同时利用0-1指示变量xij表示优化的巡视路径是否经过vi和vj两个杆塔间,xij=1表示经过,xij=0表示不经过。在二维平面上建立直角坐标系,把路径上各杆塔按横坐标从小到大的顺序排列,并要求无人机按图1所示路径优化方法,先按横坐标单调递增的路径前进,再按横坐标单调递减的路径返回出发点。

图1 无人机基于双调欧几里得TSP的巡视路径优化原理
依据上述双调欧几里得TSP的巡视路径优化方法,可建立如下优化数学模型。
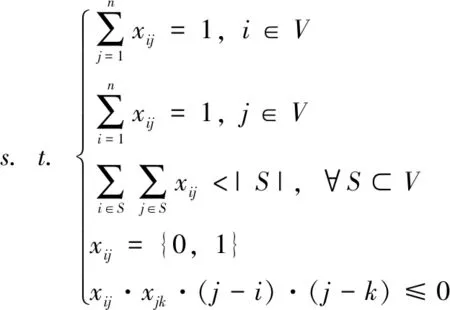
(1)
式中,第一个等式约束保证了无人机离开一个顶点刚好一次,第二个等式约束保证了无人机到达一个顶点刚好一次,第三个不等式约束保证了路径中没有子回路。第四个约束条件为指示变量,用以表明无人机是否经过两点间路径,第五个不等式约束条件用以规定无人机在两段路径上单向运动。
由于原TSP优化解的解空间会随着巡视杆塔数量的增加呈指数规律增大,并且该整数规划问题具有变量维数多,无法用分支定界法等常用的求解整数规划问题的求解器求解的特点。因此将TSP转化为式(1)所示的双调欧几里得TSP后,其优化求解具有最优子结构性质,即覆盖一个点集的最短路径是覆盖其子集的最短路径的延伸,原问题的最优解包含其子问题的最优解。基于此,可利用下述自底向上的动态规划求解方法在多项式时间内找到最优解。
定义图1中i点到j点的双调路径PATHij为从Pi从右往左到P1(最左边的点),再从P1从左往右到PJ的最短路径。该动态规划问题的子问题即为求解任意两点间最短双调路径PATHij。当i和j分别为1,2时最短双调路径明显为两点间直接路径。在此基础上从左往右依次把所有巡视杆塔加入到路径中,按照上述原则对加入的杆塔继续求最短的双调路径,并在辅助矩阵中保存子问题的最优解。在求解PATHmn时,需利用PATHij(i 构造解的规则为: 如果j=i: PATHij=min{PATHi,1+di,1,PATHi,2+di,2,...,PATHi,i-1+di,i-1} 如果j=i-1: PATHij=min{PATHi-1,1+di,1,PATHi-1,2+di,2,...,PATHi-2,i-1+di,i-2} 如果j PATHij=PATHi-1,j+di-1,i 通常在优化的无人机巡视路径上会存在已知和未知的障碍物,并且因为未知障碍物的坐标和体积不能事先确定,所以对这类障碍物的避让,需要通过增设无人机的光学或声学预警传感器,由无人机控制系统做出实时避障操作。本文考虑的是两个杆塔间优化巡视路径上存在诸如树木等自然或人为已知障碍物,因此需要在优化无人机巡视路径的基础上,进一步优化无人机在无人操纵的情况下自动避开路径中已知障碍物并到达目标杆塔的巡视路径,以提高无人机巡线效率的安全高效性。 用坐标点集{P1(x1,y1),P2(x2,y2),…,Pn(xN,yN)}表示优化的无人机巡视路径中相邻两个杆塔之间的直线飞行路径,则路径上相邻两个坐标点间的欧氏距离如式(2)所示。 (2) 令无人机在巡视路径上对已知障碍物的欧氏距离不小于指定的安全距离,则可建立式(3)所示优化数学模型。 (3) st.|OmPn| 式中,Om(xm,ym)表示两个杆塔之间已知障碍物的坐标;N表示确定无人机路径所需的坐标点数量,dsafe表示避障要求的安全距离。 对于巡视路径中如树木等点状障碍物,可用单个障碍坐标表示,对于具有较大障碍范围的飞行障碍物,可通过均匀选取多个障碍坐标表示禁飞范围,以确保无人机能够按照式(3)所示避障优化模型,确定无人机绕开巡视路径上的障碍区域。 针对避障路径优化数学模型存在搜索空间较大且约束条件和目标函数非线性,难以用传统的数学优化算法求解的问题,本文研究了基于人工势场法进行寻优的方法。该方法将巡视路径的目标点作为势能最低点,障碍点作为势能最高点。势能大小为标量,巡视路径范围内各点由来自目标点的引力势能和障碍点的斥力势能构成,两种势能取决于该点离障碍物和目标点的距离,对象靠近目标点时引力势能减小,靠近障碍点时斥力势能急剧增大,远离障碍点达到一定距离时对象不再受障碍点影响,即不存在斥力势能,以免造成避障路径寻优的频繁抖动。式(4)和式(5)分别是引力势能和斥力势能[14]的计算表达式: (4) (5) 式中,U1和U2分别是引力势能和斥力势能;α和β分别为根据经验选取的比例系数;ρ0为障碍点斥力势能起作用的最大欧氏距离;ρ1为当前巡视坐标点到目标点的欧氏距离;ρ2为当前巡视坐标点到障碍点的欧氏距离。 为了满足对象与障碍距离大于安全距离的约束条件,应满足: (7) 在程序运行时一般选取参数β>5α,此时应选取ρ0≥3dsafe即可满足安全约束。 在确定巡视路径范围内各点势能后,就可以构建无人机巡视范围内的势能场,这样无人机在势能场中的前进方向就会受到由目标点引力势能和障碍点斥力势能共同作用的虚拟力影响。将无人机巡视路径定义为式(6)所示的各点势场的梯度方向,就可以使无人机沿着各点势能下降最快的方向,以最快的速度趋向于目标点并远离障碍点,从而使选择的运动路径即可同时满足到目标点路径最短同时保持距离障碍点一定安全距离的要求。 图2 势能大小及势能梯度方向示意图 确定势场函数和步长后,从一个点出发得到的路径就是确定的,在一个点和下一个点之间选择势场梯度作为运动方向可能得到次优解,为了提高算法的最优解求解性能,在每一步增加随机扰动,多次运行图3所示寻优程序后,基于所得到的优化解集,以得到最终优化解。 图3 基于人工势场法的避障路径优化求解流程图 利用MATLAB分别编写基于动态规划算法求解双调欧几里得旅行商问题、基于人工势场法求解避障最优路径的程序,在此基础上形成考虑无人机杆塔巡视避障的两阶段路径优化程序,并分别开展以下对比仿真研究。 图4所示为某输电杆塔巡视区域,利用所研究基于动态规划求解双调TSP问题确定的无人机最优巡视杆塔路径如图4所示。利用基于模拟退火启发式算法(Simulated Annealing,SA)求解TSP的无人机巡视杆塔最优路径如图5所示。 图4 基于动态规划算法求解双调TSP确定的最优路径 图5 基于模拟退火算法求解TSP确定的最优路径 表1 两种巡视路径优化方法的比较 表1对比了两种方法用于求解最优路径的三个指标。结合图4和图5的路径优化仿真结果可知,虽然利用模拟退火算法求解TSP确定的杆塔巡视路径与利用动态规划法求解双调TSP确定的杆塔巡视路径相似,由于双调TSP要求无人机沿着一个方向离开起点,再沿着相反方向返回,所基于双调TSP问题确定的无人机巡视路径,具有转向次数和转角较小的特点,有利于避免无人机巡视过程中的频繁大幅度转向,提高了无人机巡视杆塔效率和安全性。 选取图4确定的杆塔巡视路径中两个相邻杆塔间障碍物较多的路径作为仿真对象,规划两个杆塔之间的最优避障路径。图6给出了利用图3所示寻优方法确定的避障路径。由图可见,利用所研究的基于势场法求解最优避障路径可有效避免无人机巡视路径中的障碍物。 由于人工势场法在每一步都会沿着势能降落最快的方向前进,本质上是一种贪心算法,容易陷入局部最优,所以要给算法增加随机扰动,多次运行,使之脱离局部最优。进而基于多次寻优的避障路径长短确定最优的避障路径。图7对比图6给出了避障路径在施加扰动多次寻优后确定的最优路径。 图8为无人机拟巡视输电线路的杆塔及巡视范围内的障碍点空间位置布局图。图9为采用本文提出的两阶段巡视路径优化方法确定的无人机巡视路径。路径规划结果不仅表明所提两阶段优化方法能在有效减小无人机巡视过程中的转向次数和转向角度,而且能确定有效避免飞行途中障碍物的最经济飞行线路,有利于提高自动化巡视的安全性、扩大巡视范围。 图8 巡输电杆塔与障碍物位置示意图 图9 基于两阶段优化的无人机巡视路径图 随着无人机技术的进步,全自动化的无人机精细化巡检杆塔逐渐变得可行,而巡检线路规划是无人机自动化巡检过程中重要的一环,关乎巡检的效率和安全性。本文提出了基于两阶段优化确定无人机巡视杆塔考虑避障的路径优化方法。该方法通过动态规划算法优化无人机经过杆塔的次序,通过人工势场法规划无人机在两个杆塔之间避开障碍物的飞行路径。该方法确定的巡视路径具有巡视路径短、无人机在巡视过程中转向少且转向角度小、能按照安全距离要求有效避开障碍点的特点。2 无人机杆塔巡视路径的避障优化
2.1 避障的优化数学模型
2.2 基于人工势场法的优化避障路径求解
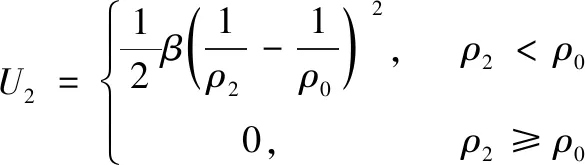
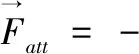
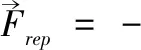


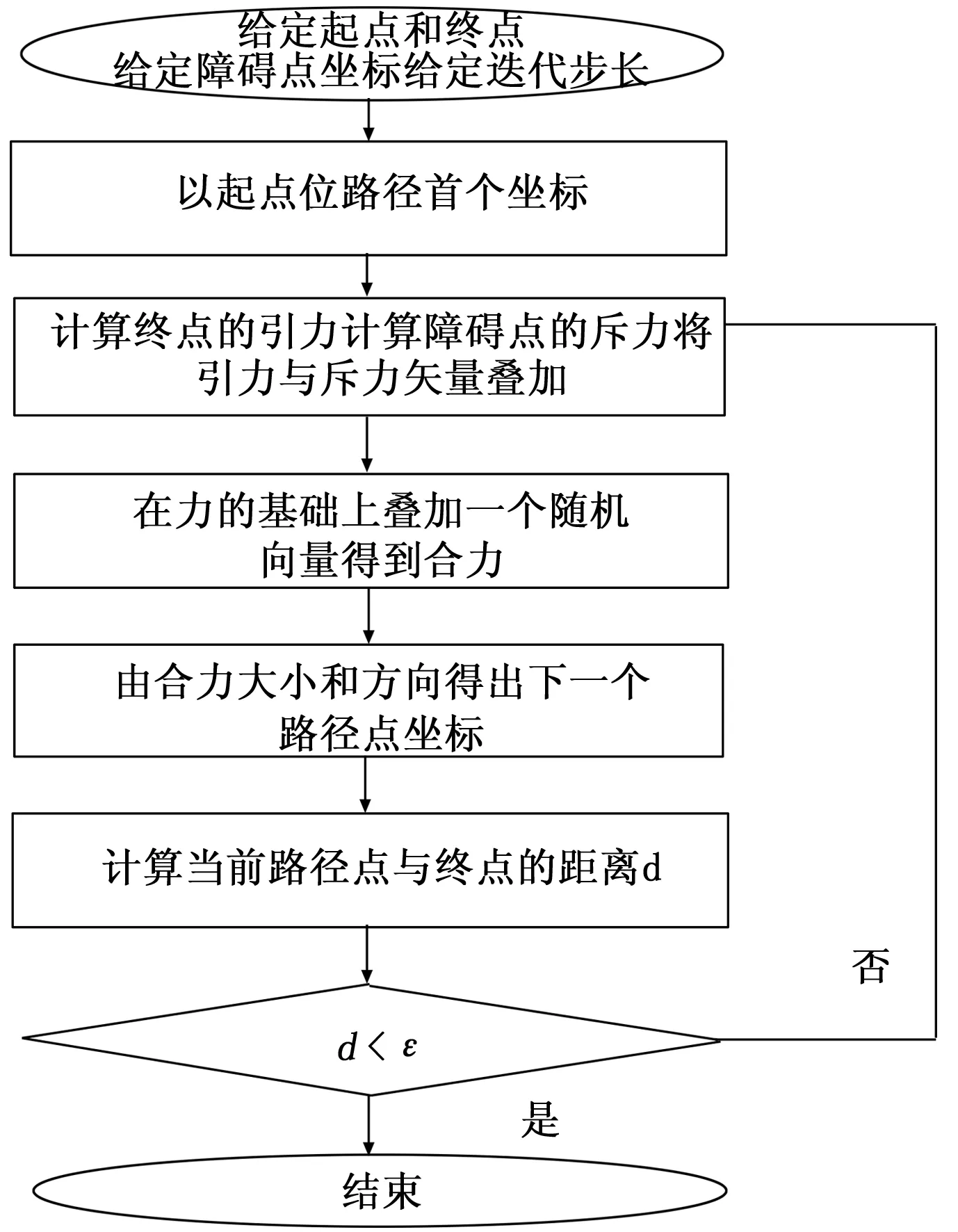
3 仿真研究
3.1 无人机杆塔巡视路径的优化

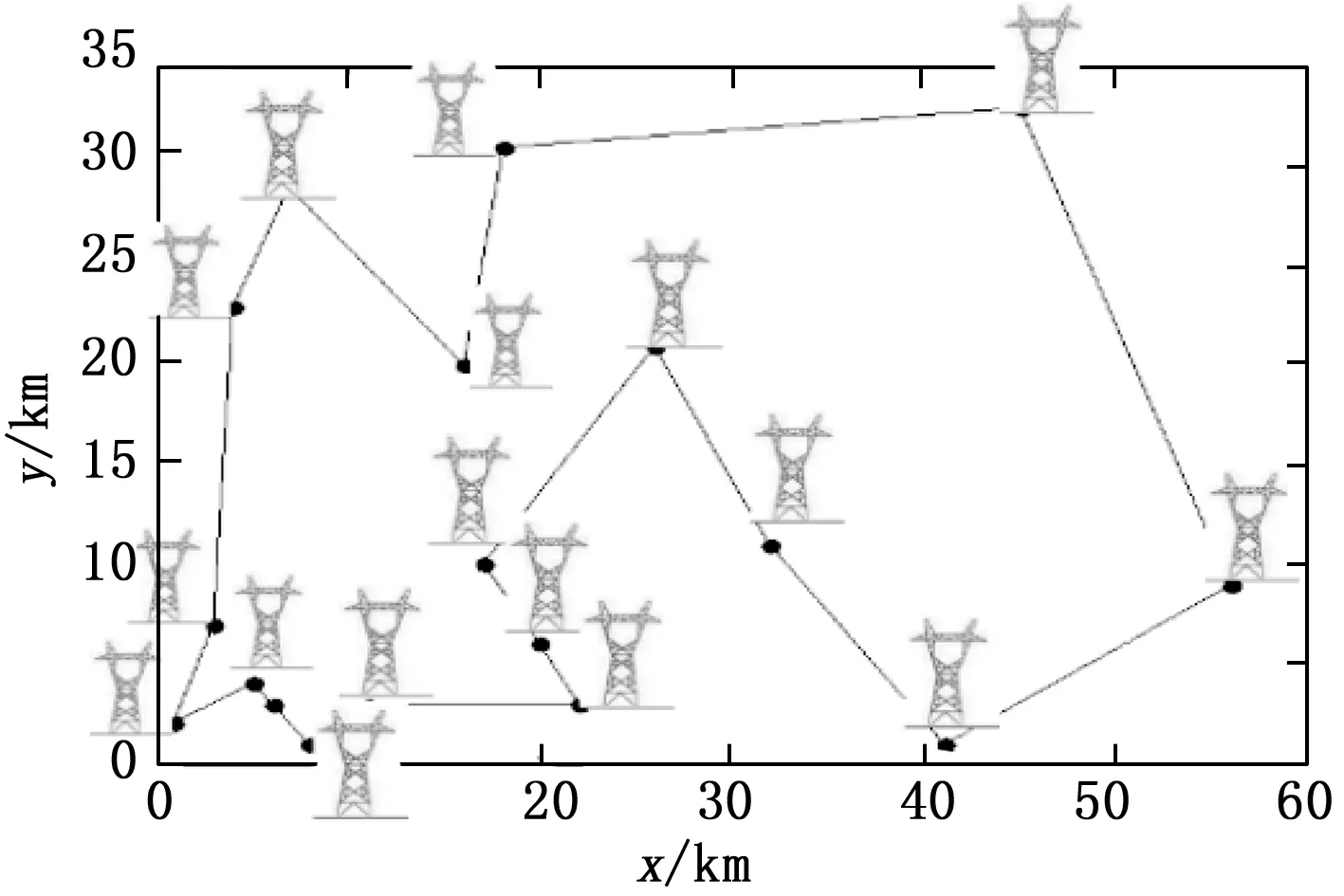

3.2 无人机避障路径的优化
3.3 考虑巡视路径避障的两阶段杆路径优化
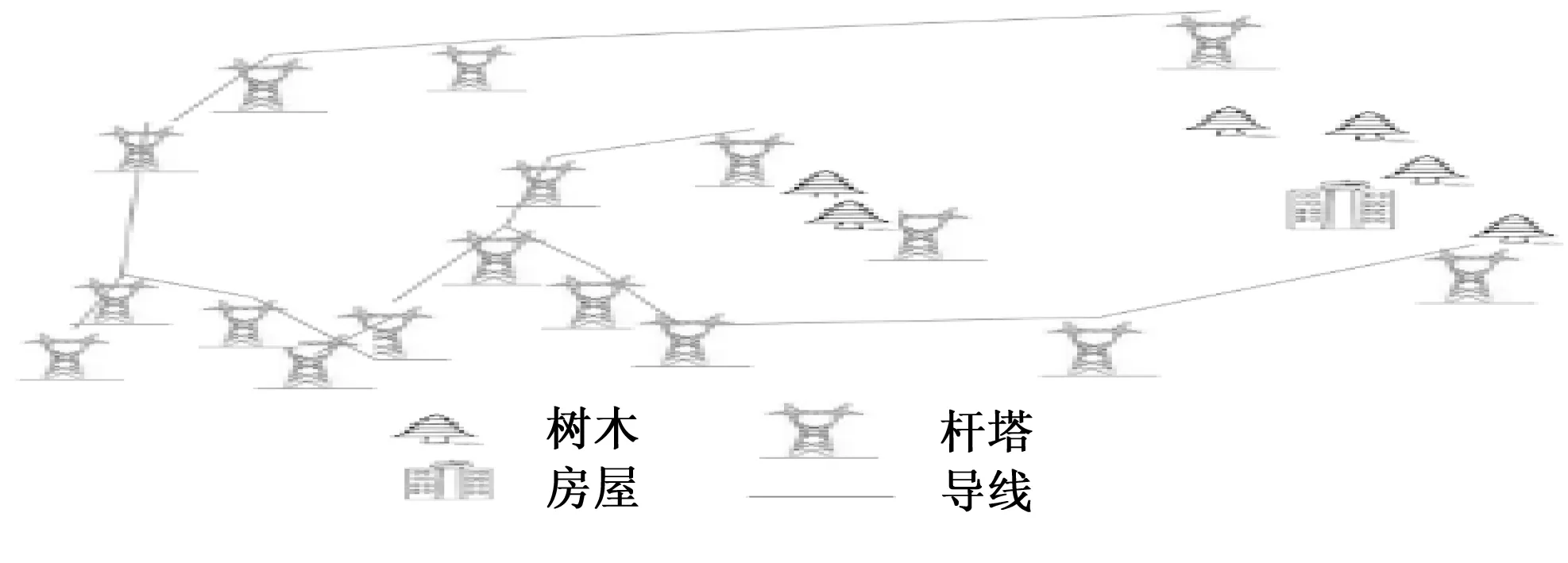
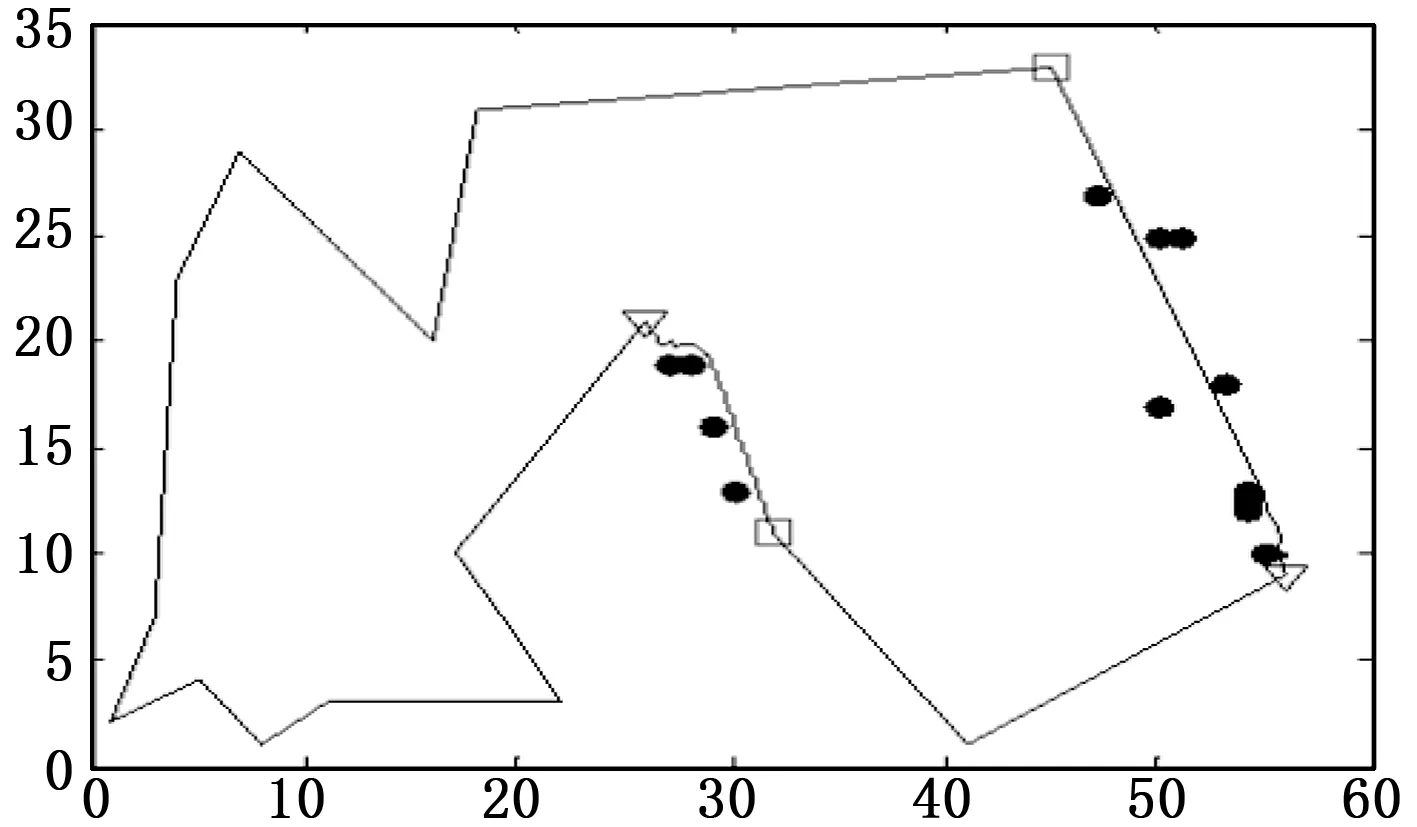
4 结束语
