无人机全包线变增益调参控制律设计

(1.北京航天无人机系统工程研究所，北京 100094; 2.海军蚌埠士官学校 信息技术系，安徽 蚌埠 233012)

0 引言

中高空长航时察打一体无人机在现代战争中起着越来越重要的作用，如已经畅销国外的翼龙、彩虹4等军贸型号。这类无人机具有多用途、滞空时间长的特点，在飞行过程中外挂任务载荷状态、起落架收放状态、燃油重量、重心以及转动惯量等参数都会发生较大的摄动，这时仅靠一套固定的控制参数难以满足无人机在大空域范围内执行多种典型任务的飞行品质使用要求。目前改善飞行器全包线飞行品质的控制方法主要包括两类：基于实时线性参变模型的现代鲁棒变增益控制方法和基于典型工况的传统变增益控制方法。文献[1-5]分别研究了鲁棒H∞变增益控制、滑模变结构控制、反馈线性化控制等现代变增益控制方法，但现代控制理论实现复杂，应用于工程实际仍需要克服重重障碍[6]。

基于典型工况的变增益控制方法可以利用成熟的线性控制理论实现非线性系统的控制，是国内无人机飞控系统设计的主要手段[7-8]。文献[9]研究了无人机程序分段PID调参方法，但控制器切换时系统性能会发生突变。文献[10]研究了无人机俯仰角增益调参的设计方法，但设计过程没有考虑质量的大幅度变化因素。

本文基于PID增益调参的思想，利用雅克比线性化方法建立了无人机的时变系统模型，研究了空速、高度、质量等参数摄动对纵向和横向飞行品质的影响，结合某样例中空长航时无人机的典型任务剖面，设计了特征点控制器并得到了增益调参调度表，最后采用参数拟合的方法得到了无人机全包线的增益调参控制器，改善了无人机的飞行品质，提升了无人机的使用性能。

1 线性时变系统建模及运动特性研究

1.1 线性时变系统建模

线性时变系统建模目前主要有3种方法：雅克比线性化方法、状态变换方法和方程替换方法。雅克比线性化方法的基本思想是在无人机全包线飞行范围内，根据不同的典型工况选取平衡点，得到一组涵盖全任务剖面的线化时不变模型，再通过插值拟合得到无人机纵向和横侧向的线性时变系统模型。状态变换方法和方程替换法是分别通过状态变换或方程替换将非线性因素去掉，从而建立系统的线性时变模型。无人机飞行过程中，质量和气动参数的摄动是缓慢变化的，雅克比线性化方法运算直观，对非线性系统的要求宽松，因此本文采用雅克比线性化方法建立系统的线性时变模型。

假设系统的非线性系统状态空间方程为：

(1)

其中：x∈Rn，u∈Rnu，y∈Rny。

利用雅克比线性化方法可得到无人机在平衡点{x0y0z0}附近的线性化模型为：

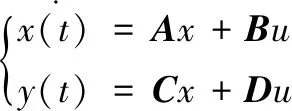
(2)

其中：

选取空速、高度、质量为参变量，在不同的工作点处根据式(2)可建立一组线性化模型，只要各平衡点处的线性化模型都是稳定的，非线性系统在平衡点附近就稳定[11]。

1.2 无人机运动特性研究

1.2.1 纵向运动特性

无人机的纵向运动表现为长周期模态和短周期模态的特性。长周期运动模态振荡周期长、衰减慢，短周期模态振荡周期短、衰减快。无人机的纵向运动特性主要取决于短周期模态，短周期振荡通常持续几秒钟，期间迎角、俯仰角和俯仰角速率剧烈变化，速度基本保持不变。对于定直平飞，无人机航迹倾角为零，同时忽略气动参数小量，根据公式(2)可以得到简化的纵向短周期传递函数为[12-13]：

(3)

式中,Mδe反映了飞机升降舵的操纵效应，Zα为理想飞机的升力系数，ξsp为等效短周期运动的阻尼比，ωsp为等效短周期自然频率。其中：

(4)

(5)

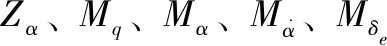
(6)

(7)

(8)

(9)

(10)

对于动稳定的无人机，Mα的值决定了短周期阻尼ξsp的大小，式(4)、(5)可分别简化为：

(11)

(12)

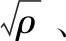
1.2.2 横航向运动特性

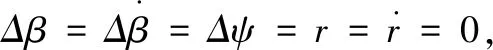
(13)

其中：Ix为无人机滚转转动惯量，b为机翼展长，Clδa为滚转力矩系数对副翼的导数，Clp为滚转力矩系数对滚转角速度的导数。由公式(13)可得滚动时间常数TL：

(14)

由公式(14)可以得出TL与ρv0成反比。空气密度ρ随飞行高度的增加逐渐减小，无人机的滚转响应会逐渐变慢，需要调节控制参数减小阻尼以提升无人机的突防机动性能。

2 增益调参控制器的设计

2.1 特征点控制器的设计

2.1.1 俯仰增稳控制器的设计

纵向短周期运动特性的改进方式主要有两种：

1)把俯仰角度q反馈到升降舵δe上；

2)把迎角α反馈到升降舵δe上。

方式q→δe经过一个积分器作为反馈，除了对动态调节因子产生有利影响外，还直接有利于减小俯仰角速度扰动qw对俯仰角速度的影响。方式α→δe也可有效的抑制纵向短周期扰动，但迎角传感器价格较为昂贵，测量代价较大，且易受到误差影响。因此为增大无人机纵向短周期运动的阻尼，俯仰角控制内回路采用俯仰角速率q反馈，使短周期阻尼满足一级飞行品质要求。外回路采用比例控制，使俯仰角能够快速跟踪参考输入。俯仰角控制结构框图如图1所示。

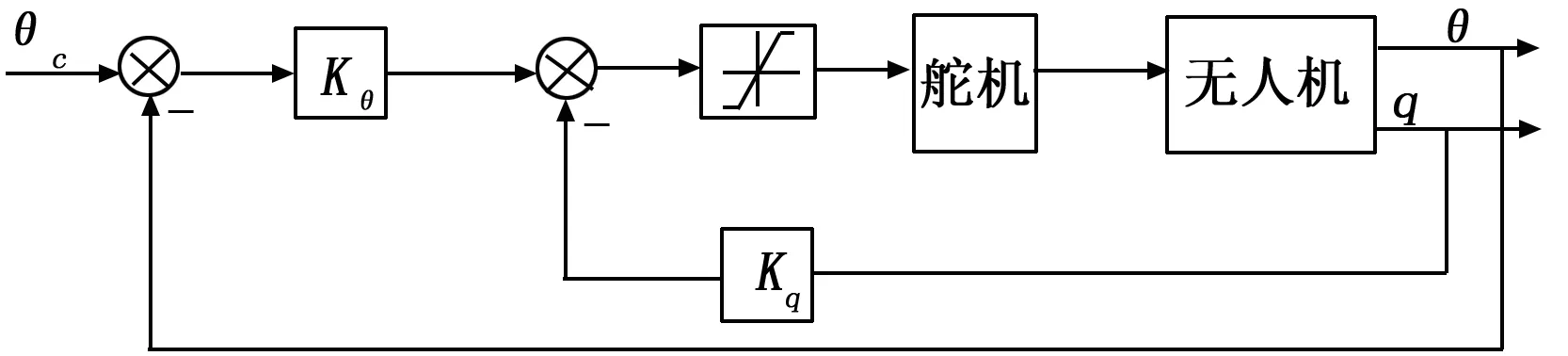
图1 俯仰角增稳控制回路框图

由图1可得到俯仰角控制律为：

Δδe=Kθ(θc-θ)-Kqq

(15)

Kθ为俯仰角比例系数，Kq俯仰角阻尼系数，Δδe为升降舵舵偏。

2.1.2 滚转增稳控制器的设计

副翼是无人机滚转控制的唯一操纵面，在改善滚转运动特性的同时，为了抑制螺旋模态和滚转模态，采用滚转角到副翼的姿态反馈(φ→δa)和滚转角速率到副翼的阻尼反馈(p→δa)相结合的方案，当滚转角φ和滚转角速率p同时反馈到副翼上时，可使螺旋模态根和滚转模态根都向左移动，并且对荷兰滚振动极点的影响也比较小，利于横向增稳系统的设计。滚转角控制结构设计框图如图2所示。

图2 滚转角增稳控制回路框图

由图2可得到滚转角控制律为：

Δδa=Kφ(φc-φ)-Kpp

(16)

其中：Kφ为滚转角比例系数，Kp为滚转角阻尼系数，Δδa为副翼舵偏。

2.1.3 舵回路设计

舵回路是增稳回路的重要组成部分，舵机的扭矩和带宽性能应与无人机的动态性能指标相匹配。为满足中型无人机轻量化、大铰链力矩使用要求，舵回路采用驱动控制电路和电机集成一体化的旋转式无刷电动舵机。电动舵机主要由电机、减速器、角位置传感器、控制电路板、接插件、壳体和摇臂组成，如图3所示。

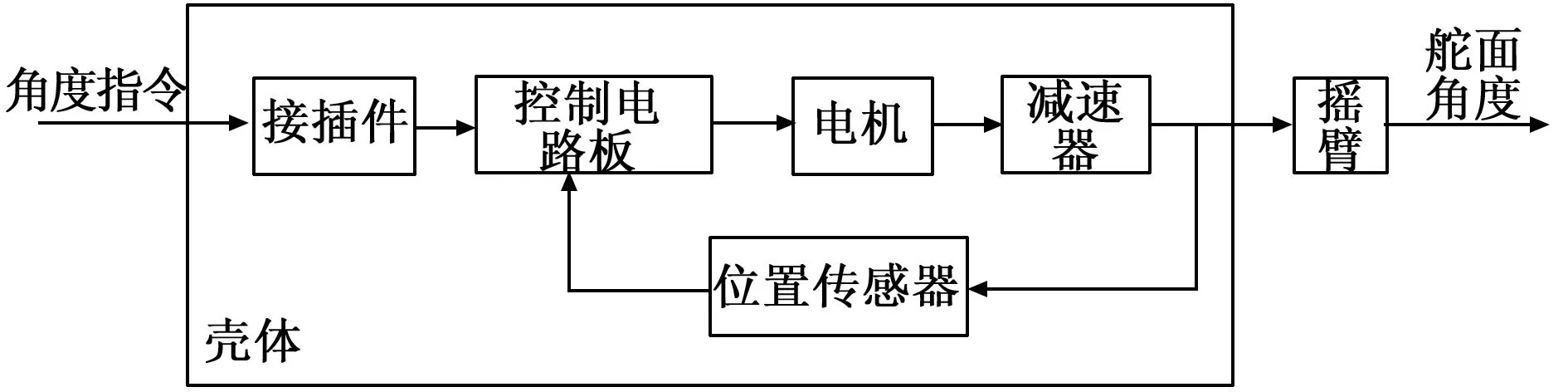
图3 舵回路组成

图4 舵回路简化结构框图

由图4可得舵回路的传递函数为：

(17)

其中：舵回路的静态增益Kδ= 1/KiKbf，时间常数Tδ=1/KAKMKbf。

参照相关文献[14-16]，舵回路的带宽应不小于无人机纵向和横向的短周期自然频率ωsp的3～5倍。通常舵机的带宽ωc可通过带载试验测定，因此可得到舵机的时间常数Tδ。为了便于测量和舵面标定，传动比Ki通常取1，角度反馈采用电位计实现，反馈系数Kbf取1，因此静态增益Kδ为1。由此可求取舵回路的传递函数。

2.2 增益调参调度表的设计

2.2.1 典型工况选取

本文所研究的样例无人机的飞行高度为0～7000 m，飞行速度为35～53 m/s，质量变化范围为520～750 kg。飞行包线及典型工况的选取如图5所示，在飞行包线内以每升高1000 m作为一个高度层，在每个高度层上结合无人机的典型质量、最小飞行速度和最大飞行速度进行配平并建立数学模型，从而设计特征点控制器。

图5 典型工况选取

2.2.2 特征点控制参数设计准则

为提高全局调参控制器的准确性，特征点控制参数设计时在各平衡点处应尽可能具有较好的鲁棒性。结合经典控制理论[17]和工程实践，得出特征点控制参数设计准则如下：

1)提高阻尼回路的阻尼比ξsp至0.76左右，改善无人机的动态特性；

2)降低系统的频率ωsp，使其稳定在6.28左右，满足一级飞行品质使用要求；

3)稳定回路幅值裕度大于6 dB，相位裕度大于30°。

2.2.3 特征点控制参数及响应

本文以纵向俯仰角控制为例研究增益调参控制器的效果，横航向全局控制器的设计方法类似，在此不再赘述。根据吹风数据，可得无人机升降舵在极限工况下的铰链力矩为12.8 N·m，纵向短周期固有频率为1 Hz，考虑结构安装要求，舵回路采用两台额定扭矩为10 N·m的电动舵机，满载频响为5 Hz，根据公式(17)可得舵回路的传递函数为：

(18)

结合无人机在各个典型工作点处的纵向短周期传递函数，可得典型工作点处的纵向控制参数及响应如表2所示，特征点(V，H，m)中V为空速(m/s)，H为海拔高度(m)，m为无人机的质量(kg)。从表中可以看出，特征点处闭环系统的阻尼比在全包线范围内维持在0.76左右，自然频率在4～7 rad/s之间，按照GJB185-86对飞行品质的规定，系统满足一级飞行品质标准。

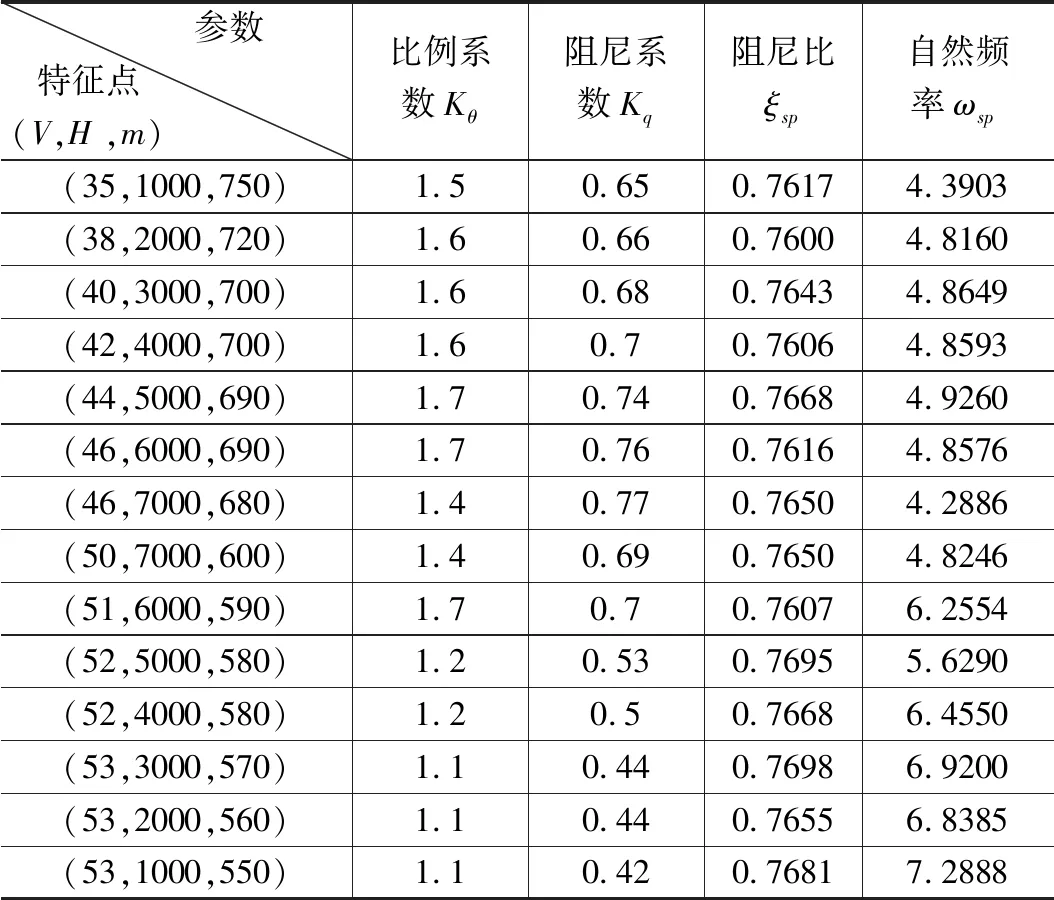
表2 典型工作点及纵向控制参数

2.3 全局调参控制器的设计

利用各特征点的控制参数，采用参数拟合的方法可得到系统全包线的调参控制器。Matlab中的sftool(X,Y,Z,W)函数提供了一个快速有效的多参数拟合方法，其中X，Y，W为参与拟合的变量，Z为拟合变量，实现方法如下：

1)将各个特征点的空速值、高度值、质量值分别组成空速矢量V、H、M；

2)将各个特征点的比例系数值、阻尼系数值组成比例系数矢量Kθ、阻尼系数矢量Kq；

3) 分别组成sftool(V,H,Kθ,M)和sftool(V,H,Kq,M)采用多项式拟合方式进行拟合。

由此可分别得到比例系数Kθ、阻尼系数Kq与空速、高度及质量的关系：

Kθ=-18.55+0.9926v-1.028×10-3h

-0.01176v2+2.007×10-5vh

(19)

Kq=0.4288-0.0161v+8.274×10-5h

-3.3317×10-4v2-8.178×10-7vh

(20)

由式(19)、(20)可以看出，对于样例无人机，控制参数主要随飞行速度和飞行高度摄动，质量的变化主要是通过改变飞机的纵向静稳定性而影响飞行品质，由于燃油、外挂武器等通常位于无人机重心位置处，质量的大幅度变化对重心位置的改变较小，因此质量变化对控制参数的摄动影响较小。

2.4 仿真验证及结果分析

根据设计的全局调参控制器，在典型的高度层上取特征点进行验证，特征点选取及频域控制性能如表3所示。由表3可以看出，拟合的控制参数能够保证无人机纵向在全包线范围内具有一级飞行品质，短周期阻尼比ξsp在±0.2以内波动，有利于无人机在不同的高度和速度下执行侦察和打击任务，一定程度上提升了无人机的使用性能。

表3 特征点验证及频域控制性能

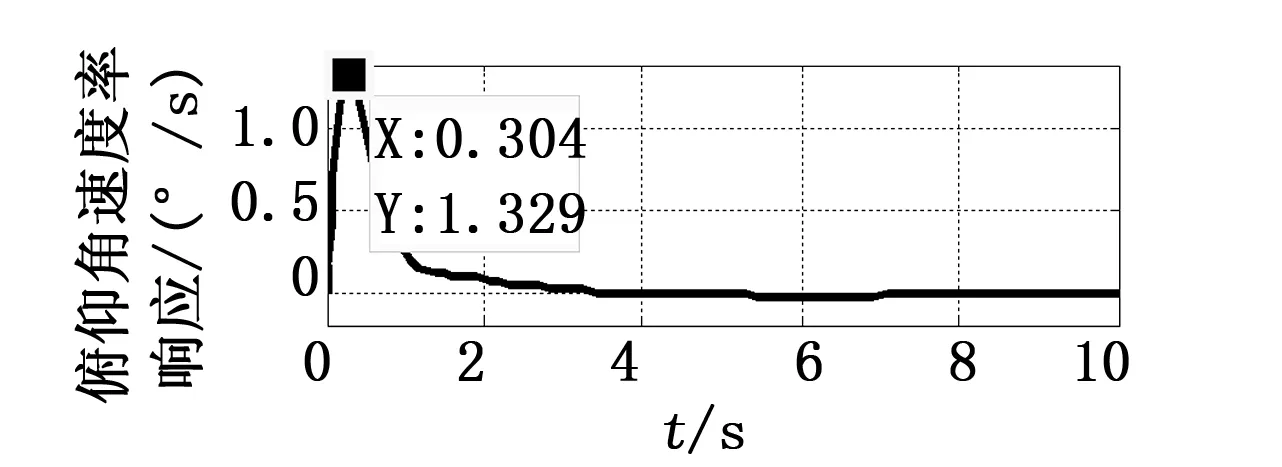
图6 俯仰角速率阶跃响应

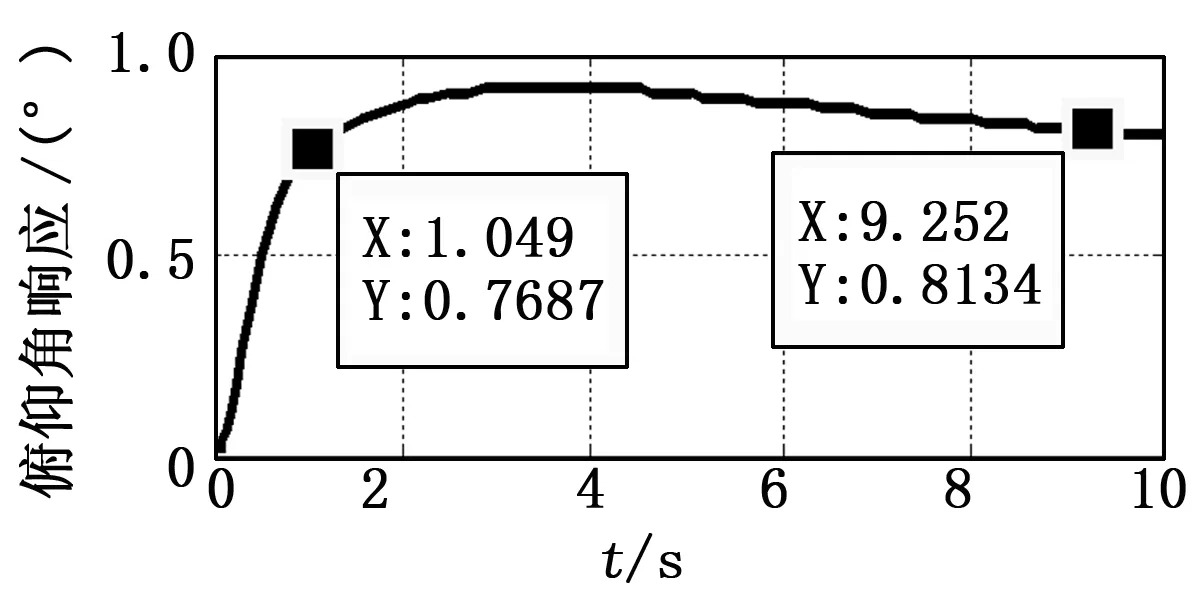
图7 俯仰角阶跃响应

图8 升降舵响应

在任意特征点(41，3500，700)处的俯仰角速率、俯仰角阶跃响应及舵偏如图6、图7、图8所示。从图中可以看出俯仰角能够快速平稳无超调的跟踪俯仰角控制指令，由于采用PD控制，稳态时存在一定的静差，静差的存在一定程度上减小了无人机定俯仰角爬升或下滑时因俯仰角超调而导致失速的风险，提高了飞行的安全性。

3 结束语

本文结合某中空长航时无人机的大包线、多任务剖面的应用需求和飞行特点，研究了无人机空速、高度、质量大范围变化对纵向和横向飞行品质的影响，利用PID变增益调参的方法，设计了全局变增益调参控制器，使无人机在全包线范围内具有一级飞行品质，在一定程度上改善了无人机的使用性能。设计过程和仿真结果表明，该方法对于飞行包线不是太大、飞行状态无急剧变化的中高空无人机实用有效，特征点建模和控制参数设计计算工作量尚可接受，通过多项式拟合得到的全局调参控制器也能保证整个系统在全包线、大尺度参数变化下具有良好的性能。但对于1万米以上、高速飞行的无人机(如高速靶机等)具有一定的局限性，后续将针对如何结合现代鲁棒变增益控制思想减小特征点模态的选取作深入的研究，扩展算法的应用领域。