中俄铁路列车脱轨稳定性判定对比研究

郝远行

(中铁二院工程集团有限责任公司， 成都 610031)

安全问题是铁路交通运输的关键，高速铁路的飞速发展对列车运行安全提出了新的挑战。一方面，与低速列车相比，高速列车一旦脱轨将引起更大危害[1]，另一方面，高速列车运行规律、性能以及运行环境等本质上有别于低速列车。然而，由于脱轨问题的复杂性，对于脱轨机理的认识目前仍停留在初级阶段[2]。

莫斯科-喀山高速铁路(简称“莫喀高铁”)在设计过程中常常存在中俄设计标准不一致的情况，其中，关于列车脱轨稳定性的判定，中俄规范有着不一样的规定。脱轨稳定性与轮轨接触关系、摩擦系数以及轨距密切相关，中俄铁路标准不同，包括轨距、轮轨接触等的不同，这些都将导致中国规范对列车脱轨稳定性的规定难以适应莫喀高铁，故不能一味地套用中国规范。中国规范对于列车脱轨稳定性统一规定为：竖向荷载与横向荷载的比值小于0.8[3]，而俄罗斯规范从原理上对脱轨稳定性进行了阐述，从而得出抗脱轨稳定性安全系数的公式，并给出了抗脱轨稳定性安全系数的限值。因此，研究俄罗斯规范关于列车脱轨稳定性的原理是非常有必要的。

1 俄罗斯规范对列车脱轨稳定性的判定

俄罗斯规范主要从列车过曲线时的运行状态、轮轨受力分析及脱轨稳定性评估等三个方面对列车脱轨稳定性的原理进行了阐述，从而推导出抗脱轨稳定性安全系数公式。

1.1 转向架曲线运行状态

列车在曲线段运行时，容易产生脱轨[4]。列车抗脱轨稳定性取决于轮对有效水平荷载和垂直载荷的比值关系。转向架轮对对钢轨施加的有效水平荷载应附加列车直线段运行时产生的纵向动力因素[5]。研究列车脱轨应首先了解转向架曲线上的运行状态，以两轴转向架为研究对象，如图1所示。

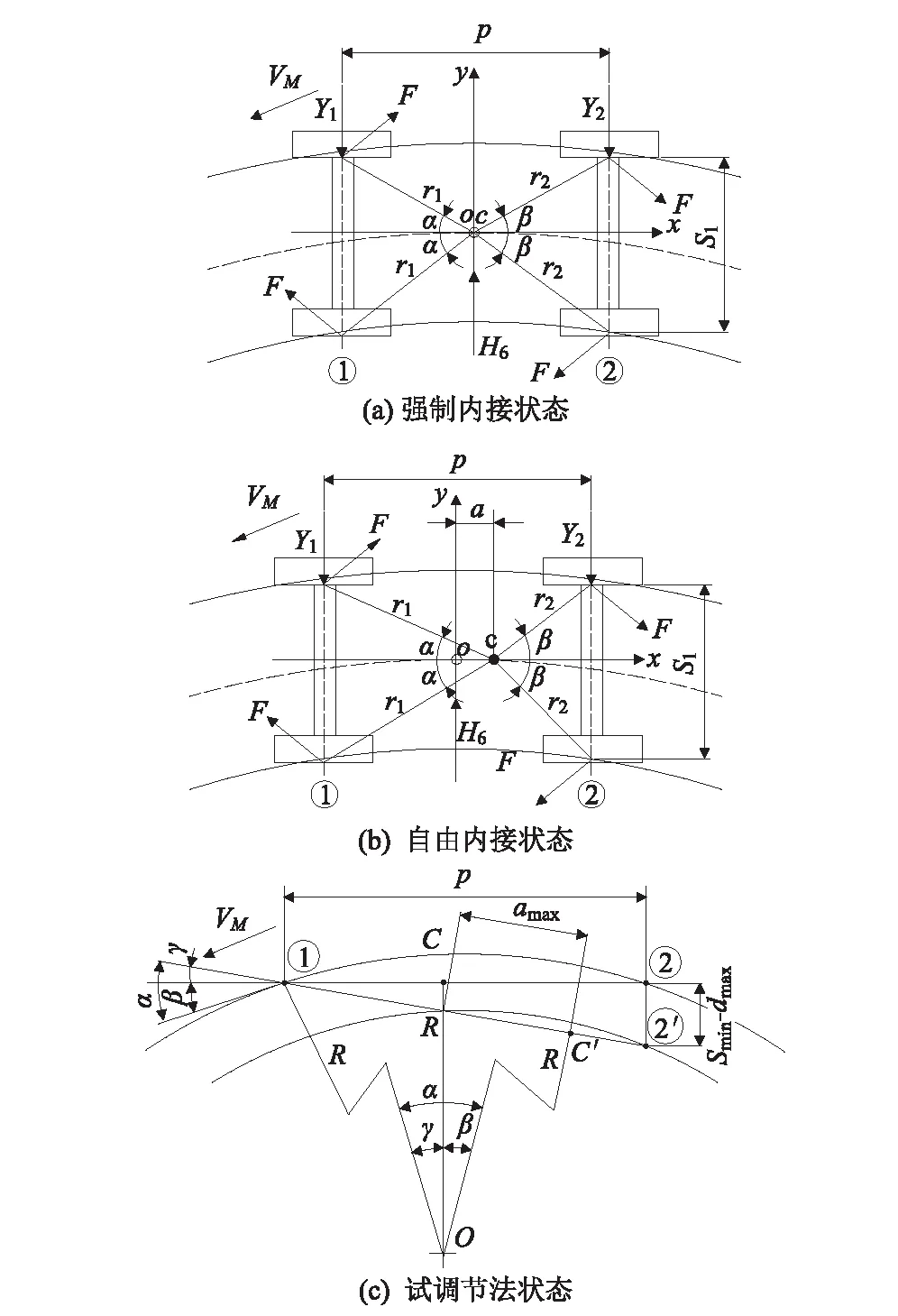
图1 双轴转向架在曲线段运行时的状态

如图1(a)所示，当转向架处于正常强制内接状态时,由于侧向力Hб相当大，1号和2号轮对的轮缘紧贴曲线外轨，产生从列车直线运行方向偏转至轮对轴向的力，即Y1和Y2。转向架中心(旋转极)C与OXY坐标系起点重合。

如图1(b)所示，当转向架处于自由内接状态时，列车运行方向前1号轮对轮缘紧贴曲线外轨，产生了一个从列车直线运行方向偏转至轮对轴向的力，即Y1。而2号轮对轮缘未与钢轨接触。此时，旋转极C向后移动了a的距离，该距离a称为极距。

1.2 曲线运行时轮轨受力分析

列车运行时，车轮与钢轨的接触点上出现摩擦力F=fPк(f为滑动摩擦系数；Pк为轮重)。按轴重平均分配进行考虑。

曲线上转向架运行状态取决于作用在列车上的有效工作载荷比，可使用试调节法解决曲线段的转向架运行状态问题。

基于此，先研究转向架处于正常强制内接状态时的情况，分析y轴投影和力矩平衡方程：

(1)

此时极距a=0。代入并解方程后得出：

(2)

其中：

(3)

如果计算得出Y1>0和Y2>0，则转向架在外轨处于正常强制内接状态；如果Y1<0和Y2<0，则转向架在内轨处于正常强制内接状态(不常见)。Y1>0和Y2<0或Y1<0和Y2>0这两种情况是转向架处于斜接状态的必要条件。Y2=0时，转向架处于自由内接状态。

研究Y1>0时这种运行状态。使用试调节法时，转向架看上去是直线切断1-2(如图1(c)所示)，位于两个极限弧形间。切断1-2的位置符合正常强制内接，切断1-2′的位置符合斜接。当转向架处于斜接状态时，转向架旋转极C移动到C’，此时极距a达到最大值amax：

amax=R×sinα-p/2

(4)

式中：α——曲线段上转向架斜接时1号轮对外轨的轮缘转动角(α=β+γ)；

β——转向架倾斜角；

γ——正常强制内接状态时1号轮对外轨的轮缘转动角。

组成角：

β=arctan×[(Smax-dmin)/p]
γ=arctan×[p/(2R)]

(5)

式中：Smax，dmin——曲线段轨道的最大宽度，根据公差和磨损得出的轮对轮缘计算点间的最小距离(dmin=1 487 mm，俄罗斯铁路为 1 520 mm轨距)。

根据上述平衡方程式组成并消除相对侧向力后，可得：

Y1=Hσ-Y2+2F(cosα1-cosα2)

(6)

(7)

式中：a——极距(转向架斜接时a=amax)。

角度和半径(见图1(b))根据公式确定：

(8)

cosα1=(p+2a)/(2r1)
cosα2=(p-2a)/(2r2)

(9)

如果计算斜接状态，即Y1> 0和Y2< 0，则停止计算侧向力。当Y2<0时，需研究可确保列车稳定运行的转向架自由内接状态。为了准确测定转向架自由内接状态时的侧向力Y1，运用程序循环计算原则，循环计算使得2′(如图1(c)所示)接近点2，当条件Y2=0时符合规定值，则停止计算，从而得到准确的Y1值。侧向力Y1是获得列车动力学函数Y1=f(v)和计算抗脱轨稳定性的主要参数。在列车运行时，曲线上作用在轮对上的外加力如图2所示。施加在轮缘和轨顶内缘上的侧向力Y是这些构件的主要磨损参数。

Y——指向轮缘的力；Ftр——车轮与钢轨接触处的水平摩擦力；Yр——沿轮对轴线的框架力，Yр1=Y-Ftр；Р1和Р2——垂直有效载荷；N——钢轨的反作用力，其方向垂直于轴线y并作用于轮缘工作面，轴线y与水平线成βp角；Ftр =f×N——沿轴线y方向作用的内聚力(车轮滚上钢轨)图2 计算轮对抗脱轨稳定性示意图

1.3 脱轨稳定性评估

在车轮与钢轨不良相互作用力组合下，除车辆横向或纵向倾倒外，还会发生车辆(转向架)轮对的轮缘爬上轨顶，随后脱轨。

当轮缘对钢轨的水平侧向压力Рg=yр1+fР2以及轮缘与钢轨的摩擦力变得非常大时，在这些力的作用下，车轮抬起并爬上轨顶踏面，仅靠轮缘支撑。在y轴面上成βp角爬上轨面。在这种情况下，垂直负载Рb=Р1不能克服摩擦力，车轮升高，紧靠轨顶踏面并向下滑落。继续运行，车轮轮缘爬上轨顶踏面，在水平力的作用下滚过轨顶，从而脱轨[6]。Рg与Рb的比值越大，脱轨概率就越大。

脱轨常发生在因曲线维护不良，平面上产生侧向力的地段，特别是当侧向力与线路纵向不平顺造成的车轮局部卸载同时发生时。车体及转向架弹簧刚度和线路不平顺幅度越大，车轮卸载将越大，从而有可能造成列车脱轨[7]。

为了评估稳定性，按照下式把垂直力和水平力的计算比值与临界比值加以比较[6]：

(10)

坐标系Oxy中力的平衡方程式：

N-Pb×cosβp-Pg×sinβp=0

(11)

f×N-Pb×sinβp+Pg×cosβp=0

(12)

因此，待分析接触点上的垂直载荷和水平载荷临界比值为：

(13)

则抗脱轨稳定性安全系数：

(14)

这是俄罗斯规范对于列车脱轨稳定性的判定。

2 中俄规范对列车脱轨稳定性判定的对比

中国TB 10621-2014《高速铁路设计规范》中对列车脱轨系数的规定为[2]:

(15)

俄罗斯规范对列车脱轨稳定性的判定为计算抗脱轨稳定性安全系数，与中国规范的判定方式有所差异。为比较中俄脱轨稳定性判定的差异，将俄罗斯规范的抗脱轨稳定性安全系数公式进行变换可得：

(16)

根据莫喀高铁设计中的轮轨接触参数，摩擦角βp=60°，摩擦系数f=0.25，将其带入上式可得：

(17)

综上所述，中俄规范对于列车脱轨稳定性的判定均与轮对受到的水平荷载和竖向荷载的比值有关，而俄罗斯规范还增加了轮轨摩擦角、摩擦系数等参数的引入，针对莫喀高铁设计，俄罗斯规范计算的脱轨系数相对于中国规范规定较为严格。

3 结论

俄罗斯规范关于列车脱轨稳定性的判定与轮对受到的水平荷载和竖向荷载的比值、轮轨摩擦角、摩擦系数及轨距均有关系。对列车过曲线时的运行状态、受力情况进行了分析，并从原理上解释了列车脱轨的过程，从而得出了抗脱轨稳定性安全系数。

计算结果表明：中国对列车脱轨系数Pg/Pb<0.8的规定较为笼统，难以适应莫喀高铁的标准，经转化俄罗斯规范规定的抗脱轨稳定性安全系数公式，采用莫喀高铁设计中的车辆参数，计算得出列车脱轨系数Pg/Pb<0.74，经对比，俄罗斯规范对于列车脱轨稳定性的判定相对于中国规范较为严格。为了适应俄罗斯规范规定要求，在莫喀高铁设计中，脱轨系数限值建议采用0.74较为合适。