多维固有时间尺度分解算法
2019-05-07彭秀艳刘元勋
彭秀艳, 刘元勋, 郑 潜
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150020)
0 引 言
故障检测与诊断在控制回路、机械系统中具有重要的地位,若能在设备运行仍处于可控阶段时准确及时地检测出故障的萌生及演变,并将其解决可以避免非正常工作状态,保证设备正常运转,对保障系统安全运行,减少或避免重大灾难性事故具有非常重要的意义[1~4]。可通过处理、分析非平稳多维信号,提取故障特征[5,6]。Rehman N和Mandic D P提出了多维经验模式分解(multi-dimensional empirical mode decomposition,MEMD),实现了经验模式分解(empirical mode decomposition,EMD)的多维扩展[7]。
本文对Mark G F和Ivan O提出的固有时间尺度分解(intrinsic time scale decomposition,ITD)进行多维扩展,提取出某控制过程多维输出信号中的频率相近的故障成分,为后续评估过程是否存在故障行为提供数据[8]。
1 多维固有时间尺度分解
本文所提出的多维固有时间尺度分解(multi-dimensional intrinsic time scale decomposition,MITD)的提出参照了MEMD的扩展方法。本节将先介绍几种处理非线性、非平稳信号的算法,并进行仿真实验给出实验结果分析。
1.1 EMD
EMD是在时间尺度上将原始信号分解为一系列本征模态函数(intrinsic mode function,IMF)分量和余项r[9],即
(1)
式中X(t)为原始信号,imfi(t)为第i个本征模态函数,l为本征模态函数的个数。 IMF需满足以下条件:1)在整个数据序列中,极值点的数量与过零点的数量相等或只相差一个;2)在任一时间点上,信号的局部最大值和局部最小值定义的包络线的均值为零。
每一层IMF筛选停止条件通过限制标准差的数值大小来完成,如式(2)所示
(2)
当SD在0.2~0.3之间时,停止筛选循环。
1.2 ITD
ITD同EMD相似,将原始信号分解为由瞬时频率和瞬时幅值组成的一系列由高频到低频的旋转分量和单调趋势项两部分[10,11]。
设Xt为待分解的实值离散信号,定义L为基线提取算子,Lt为基线分量,Ht为固有旋转量。定义Xk表示X(tk),Lk表示L(tk) 。ITD算法计算步骤如下[8]:
1)提取Xt序列的极值点Xt和对应时间{τk,k=1,2,…,N},并定义τ0=0。在区间(τk,τk+2]上,定义线性变换公式为
(3)
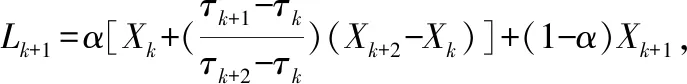
2)提取出固有旋转分量Ht
Xt=LXt+(1-L)Xt=Lt+Ht
(4)
3)将基线信号Lt作为待分解信号重复步骤(1)、步骤(2),当Lt单调或幅值小于阈值时终止分解。
ITD作为一种不受时频不确定影响的局域波分解方法能够得到更高的时间分辨率和频率分辨率;相比于EMD,ITD过程中没有复杂的筛选和插值,具有计算复杂度低、计算速度快的优点,在线分析实时信号时具有更大的优势;其边缘效应只出现在第一个过零点之前。不会随着信号分解向内部数据传输[12,13]。
1.3 MEMD
使用基于信号投影来产生多维信号包络。设信号为n维,首先在n-1维球面上选取不同的方向向量;然后将原始信号投影到各个方向向量上,在各个方向上取极值点;再将这些极值点映射到原信号上,通过三次插值找到对原始信号包络的估计;最后,取各个方向包络的均值,得到期望均值[14,15]。MEMD在保留了EMD优势的基础上,将该算法扩展至多维数据分析邻域,对其他一维分解算法扩展具有指导意义。
2 MITD算法
2.1 扩展思路
仿照MEMD扩展思路,取多维信号上的极值点,对极值点运用多维基线节点提取公式,整合节点和极值点,利用多维线性变换方法,得到均值信号,从原信号中剔除均值信号,得到一层分解子信号。经过多次循环,得到一系列旋转子信号和一个趋势信号。
该扩展思路涉及3个关键点:1)多维信号极值点的定义;2)多维基线节点公式的提出与证明;3)线性变换因子及多维线性变换方法的合理性。
2.2 多维极值点的定义
原信号中切线方向与投影方向垂直,且切线变化的方向均不垂直于投影方向的点。可知,有且仅有投影信号的极值点,在原信号上的对应点,是原信号投影方向的极值点。
2.3 多维基线节点公式
(5)
直线AC与平面τ=τj的交点为b(mj,nj,τj),且mj,nj满足
(6)
B点和b点之间的连接向量为
(7)
根据线性缩放关系可得
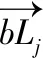
=((1-α)(Xj-mj),(1-α)(Yj-nj),0)
(8)
式中o为坐标原点,由此可得
=((1-α)Xj+αmj,(1-α)Yj+αnj,τj)
为打通农商行进入资本市场的渠道,应由上级部门(如省联社)等进行主管,协同各区域农商行进行集中出资,来设立农商行股权交易信息中心,实现股权登记、质押、挂牌、托管等多功能,同时结合当地农村区域发展状况,可以将债权、土地承包权、金融资产及林权等在交易中心来办理交易及托管,将其打造成适用于农商行的战略平台。除此之外,农商行应建立健全股权流通的相应机制,完善交易流程及运行规则,对股权转让、设置及信息披露来进行明确规定,严格规范股权在交易中的操作细则,将制度进行市场化、透明化,使得广大股东充分明晰自身的权益,构建科学规范、合法、高效的农商行股权流动机制,实现股权的正常化,发挥农商行股权的真正价值。
(9)
即点Lj的解析表达式满足
(10)
推广到n+1维中,可位于τj时刻的基线节点Lj(m1,j,m2,j,…,mn,j,τj)解析表达式(i=1,2,…,n)
(1-α)Xi,j
(11)
2.4 多维线性变换公式
在区间(τk,τk+1]内,n维信号在t时刻为Xt(x1t,x2t,…,xnt),投影方向向量为q(a1,a2,…,an),原信号在该投影方向对应的两个基线节点为Lj(m1,j,m2,j,…,mn,j),Lj+1(m1,j+1,m2,j+1,…,mn,j+1)。
由式(3)所示的一维线性变换公式,定义线性变换因子Pt为
Pt=(Xt-Xk)/(Xk+1-Xk)
(12)
类比得到多维线性变换因子Pt为
(13)
由Pt得Xt的线性提取结果为
LXt={Lx1t,Lx2t,…,Lxnt}
(14)
式中Lxit=mi,j+(mi,j+1-mi,j)Pt
3 算法优化与应用试验
3.1 算法优化
在MEMD中使用的Halton序列的低差异性会随着维度的上升呈指数下降。所以,在MITD中利用一种新的低差异序列Sobol序列来代替Halton序列来选择原信号的投影方向,以适应更高维度的信号分解。
3.2 仿真分析
由于MITD,ITD和MEMD都没有明确的解析公式,只能通过相应算法来定义,因此,比较的过程建立在数值仿真的基础上。四维仿真信号x各个维度信号如式(15)所示。为了突出MITD在保留信号局部特征方面的优势,选用三角波作为测试信号。对其分别进行MITD,ITD和MEMD,并对比分析这三种算法
(15)
式中 sawtooth(2πfit)为频率为fi(i=1,2,3,4),幅值为1,关于零线对称的三角波;xf为0.5 s时产生的一个持续时间0.05 s,12 Hz的三角波震荡;f1=10 Hz,f2=20 Hz,f3=50 Hz,f4=100 Hz。
采样时间1 s,采样频率fs=1 000 Hz,分解结果对比如下:
标准ITD多维信号时,易出现模式不齐整和模式混淆,且难以检测故障信号。而在MITD的分解结果中,克服了这些问题。虽然MEMD和MITD都可以无混淆的分解多维信号,且检测出故障信号。但由于MEMD采用三次样条插值,导致分解结果趋向正弦,难以反应信号的本质特征。
3.3 工业实例分析
从某工业控制回路中,取5个回路的1 500个采样点测试信号。MITD分解工业信号的结果如图1所示。其中,第1层为高频噪声H1、H2的叠加,第4层为残差。计算时域的零交叉点规律性指标判断是否有振荡发生。
由表1可知,H3层各回路对应的振荡检测指标均小于1,未被判定为发生振荡;H4层中各回路对应的零交叉点规律性指标均超过给定阈值1,说明这些分解子信号均为振荡分量;检测到5个回路同时存在振荡,因此可以判定为厂级振荡。由图1可以看到有一个轻微的振荡在N=1 000时进入到工业回路中在回路之间传播,并在N=1 250之后被校正,没有造成明显的过程振荡。该振荡被MITD准确提取,充分证明了该算法提取多维信号局部特征的能力。
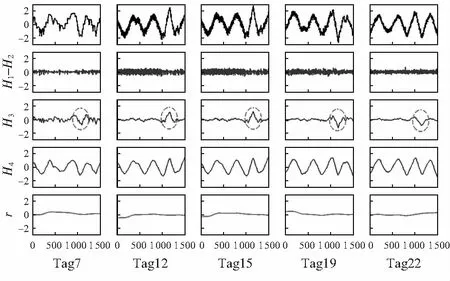
图1 MITD对工业实例分解结果

变量回路7回路12回路13回路19回路22H30.490.690.560.4800.594H42.682.682.602.8203.226
4 结 论
本文在已有的EMD,ITD,MITD算法基础上,提出了多维数据分解的新方法—MITD,通过极值点的定义、多维基线节点提取公式以及多维线性变换公式这3个关键点来完成算法扩展。试验仿真结果表明:相较于EMD和MEMD算法,MITD算法分解效率高,端点效应小,局部特征明显,是一种有效的多维信号处理方法。
