基于计算机显微视觉的微动平台位移测量方法*

2019-05-07朱永波卢国梁

传感器与微系统 2019年5期

朱永波，卢国梁

(1.山东大学机械工程学院，山东济南 250061; 2.山东高效洁净机械制造教育部重点实验室，山东济南 250061)

0 引言

现代科学技术正向微型化、精密化快速发展，微、纳米技术甚至被誉为十大可改变世界的科技之一[1]。微动平台作为微纳米技术中的一个重要执行元件，广泛应用于微装配、细胞注射、微操作等[2～5]，其输出位移的检测技术作为微纳操控精度的关键，得到越来越多的研究。目前采用光栅和激光尺[6,7]对安装位置要求十分严格，容易被遮挡等特点导致其往往难以应用于多自由度微动系统中；另一方面，对于微装配合、细胞操作等一些需要可视化操作的场合下，光栅和激光尺也难以满足测量要求。

基于计算机视觉的测量方法以其高精度、可视化、可适用于多自由度系统测量等特点而成为研究热点，越来越多的学者也进行了一些显微视觉的测量研究。Davis C Q[8,9]、张宪民[10]和谢勇君[11]等人结合计算机视觉及频闪成像测量微运动，但图像处理算法时间复杂度较高，难以满足实时测量要求；Clark L[12]和陈文海等人[13]利用图像边缘特征配准计算微动平台输出位移，方法简单，但精度相对较低；黄赞等人[1]利用单演曲率张量与数字图像相关法测量微位移，鲁棒性较好，可实现亚像素级精度，但算法较为复杂，难以实现实时测量。

针对以上问题，本文提出了一种基于计算机显微视觉的微动平台测量方法。并通过实验验证，证明了该方法具有测量精度高、效率高、可视化、成本低以及适合多自由度微动平台测量的特性。

1 微动系统与成像模型

本文所述基于桥式放大机构的微动平台如图1所示[14]，其主要由基于三角放大原理的桥式放大机构和平行四边形导向机构组成。工作时，压电换能器(piezoelectric transducer,PZT)驱动桥式放大机构，使得微动平台输出部分在平行四边形导向机构作用下沿x轴方向运动，其行程可达数十微米(μm)。

图1 微动平台

为测量微动平台输出位移，本文设计了显微视觉系统。该系统由CCD相机、显微镜(放大倍数×5～50)、微动平台、标记物(硅基镀金膜)以及一台计算机(Intel Core i3—4170 CPU 3.7 GHz 4 GB RAM)组成。系统成像模型可简化为一针孔模型[15]，其成像关系如图2，根据图2，图像坐标系和固连于微动平台的坐标系变换关系为

(1)

式中θ为Oximg和O0x0的夹角；c1，c2为原点O′到O0的平移关系。对于本文中的单自由度系统，式(1)可简化成

x0=kximgcosθ+kyimgsinθ+kc1

(2)

式中k，θ及c1均可由相机标定获得。

图2 小孔成像模型

2 基于二值化图像的重心的位置计算

2.1 二值化处理

标记物在微视觉成像系统中成像如图3(a)，通过图3(b)其灰度直方图可以看出，其灰度值分布主要集中在2个区间，基于此特点，对灰度图像进行二值化处理

(3)

式中λ为阈值，其由Ostu法[16]确定。

图3 微视觉图像及其灰度直方图

2.2 滤波与连通域提取

由于噪声等影响，二值化后的图像在连通域内存在一些“小孔”以及“间隙”，进行形态学滤波处理

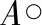
(4)

Xk=(Xk-1⊕B)∩A,k=1,2,3,…

(5)

式中当Xk=Xk-1时停止迭代，此时Y=Xk，连通域提取完成。同时，剔除面积小于特定阈值的连通域以消除噪声影响。

2.3 重心位置计算

如图4(b)，经过滤波后的图像由3个连通域组成，其中连通域3在整个微动平台运动过程中一直在视场内，因此，可以追踪连通域3的重心坐标位置，计算微动平台输出位移。重心位置计算公式如下

(6)

式中Y3为连通域3，将式(6)获得的重心坐标代入式(2)中，可求得微动平台输出位移。

图4 二值化及其闭合运算后图像

3 实验验证

为验证本文方法的有效性，对微动平台进行了测量实验，并对比了基于图像块匹配算法[17]的位移测量。实验中，以累积均方误差(mean square error,MSE)评价各测量方法的精度

(7)

式中xi,ref为由光栅尺测量得到的第i个采样点数据，由于光栅分辨率(1 nm)远高于显微视觉的测量精度，因此，选取其作为实际位移量的参考值，xi为其他方法测量的位移值。

3.1 阶跃信号与正弦信号测量误差及效率

图5为当微动平台以阶跃和正弦信号运动时，本文方法和图像块匹配方法的测量结果。

图5 微动平台沿不同信号运动时位移测量结果

当微动平台以阶跃信号方式移动时，基于图像块匹配算法的累积方误差为0.142 μm，本文方法的累积均方误差为0.163 μm；而当微动平台以正弦信号移动时，基于图像块匹配算法的累积均方误差为0.229 μm，本文方法的累积均方误差为0.231 μm。两种方法测量误差比较接近，但本文方法每帧图像处理时间约为4.19 ms，而基于图像块匹配的算法每帧图像处理时间约为14.46 ms，本文方法效率远高于基于图像块匹配算法。

另外，对于阶跃信号，在微动平台t=1 s处突然运动，微动平台动的瞬间速度较大，CCD相机采集的图像较为模糊，因而对图像二值化过程造成较大影响，图6(a)记录了不同时刻连通域3的面积变化，其中，直线是面积平均值，曲线是各时刻连通域3面积大小，从图中可看出，在时刻t=1 s处，连通域3的面积发生剧烈变化，所对应的瞬间测量误差较大，图像较为模糊；而对于正弦信号，由于微动平台运动相对平缓，因而连通域3面积变化不大，各个时刻测量误差相对稳定。

图6 连通域3在各不同采样时刻面积变化

3.2 成像模型验证

由于微动平台是单自由度系统，根据上文所述针孔成像模型，根据式(2)，微动平台在图像空间的运动轨迹应该为一条直线。为验证成像模型，图7记录了微动平台沿1/4个周期的正弦信号运动时连通域3的重心坐标，其中,三角是不同时刻采样点连通域3的坐标，直线为采用最小二乘法拟合的直线。可以看出：连通域3重心坐标基本符合直线分布，证明成像模型有效。