基于上海市地理国情成果的学生就学可达性测度与学区优化分析
2019-05-07李淑瑶忻静
李淑瑶,忻静
(上海市测绘院,上海 200063)
1 引 言
随着我国经济社会的高速发展,我国的基础教育水平显著提高、教育实力得到了大幅度提升,但是由于各区域之间的教育水平存在差异,部分地区依然存在教育资源不均衡的情况。
地理信息系统技术大量应用于资源管理、环境监测、城市规划、土地管理及交通、水利、林业等领域,在教育领域也得到应用。
近年来,国外很多学者利用GIS对学校与社区整体规划、学校布局的优化调整,学区优化模型、交通成本与学区划分两者之间的关系等进行了深入的研究。20世纪80年代初,GIS开始应用于教育地理研究,美国华盛顿于1994年举行了“全国GIS在教育中的应用”(简称EAGIS)会议,会议上讨论了EAGIS的开发前景和展望。Taylor G等(1999)利用GIS对北卡罗来纳州约翰斯顿县的学校和社区进行了整体规划,成功降低了交通对入学的影响程度[1]。Caro F等(2004)提出了一个基于GIS的学区布局优化模型,并以美国费城的学区为案例进行模型的验证,认为结合定性分析与定量分析能够有效地解决学区划分的问题[2]。Hanley等(2007)对艾奥瓦州学校进行了调研,采用GIS技术分析了交通成本与学区划分之间的关系,并计算了学区合并对交通成本的影响[3]。
国内将GIS应用于学校布局的研究相比于国外相对较晚。目前国内教育设施空间布局的研究主要集中在教育设施布局规划、优质教育资源的配置、入学可达性以及学校规划调整方面。2004年我国着手研发了“北京市教育资源布局电子地图”,构建北京教育地理信息系统,为北京学校布局决策提供科学依据。孔云峰(2012)以就近入学为目标,构建学区划分优化模型,利用线性规划算法和GIS技术对中小学的学区进行了最优划分[4]。周子懿(2015)通过采用GIS技术对比控规单元和学区划分所形成的不同空间层次对小学的供需状况和可达性水平的影响,进而说明学区划分对小学实际服务能力的影响[5]。
上海市作为我国的超大型城市,无论是经济总量、人口总数还是城市规模都处于领先地位,而庞大的城市规模和复杂的城市背景也必将导致城市管理和转型升级方面充满难题。在教育资源配置方面,上海选择分区划分学区的方法进行管理,其他大型城市也多选择此种方法管理教育资源。可达性反映了服务区位与供需平衡的关系,是资源配置合理性评价的重要参考,城市的发展对学区优化提出了更高的要求。因此,在学区对口的前提下判断小学可达性,确定更优的学区划分方案,是大型城市进行教育资源均等化分析的必要内容。
在现有研究的基础上,本文在ArcGIS平台下利用多种方法,根据小学与居住小区之间的空间位置与小学资源现状,实现小学可达性的量化评价,进行学区划分优化探索,为大型城市中政府教育资源配置与管理提供参考。
2 研究区域及数据准备
2.1 研究区域介绍
普陀区以境内普陀路得名,故称“普陀区”。位于东经121°39′,北纬31°25′,地处上海市中心城区西北部。东起沪太路、彭越浦、苏州河与闸北区交界,南沿苏州河、万航渡路、长寿路、安远路与长宁、静安区毗邻,西至沪宁铁路、环浜与嘉定区接壤,北达真南路、薛家浜、灵石路与嘉定、宝山区相连。辖区内苏州河东西穿越而过,距市中心人民广场 7.5 km。总面积 55.53 km2,其中水域面积 1.65 km2。上海市普陀区街道划分如图1所示:
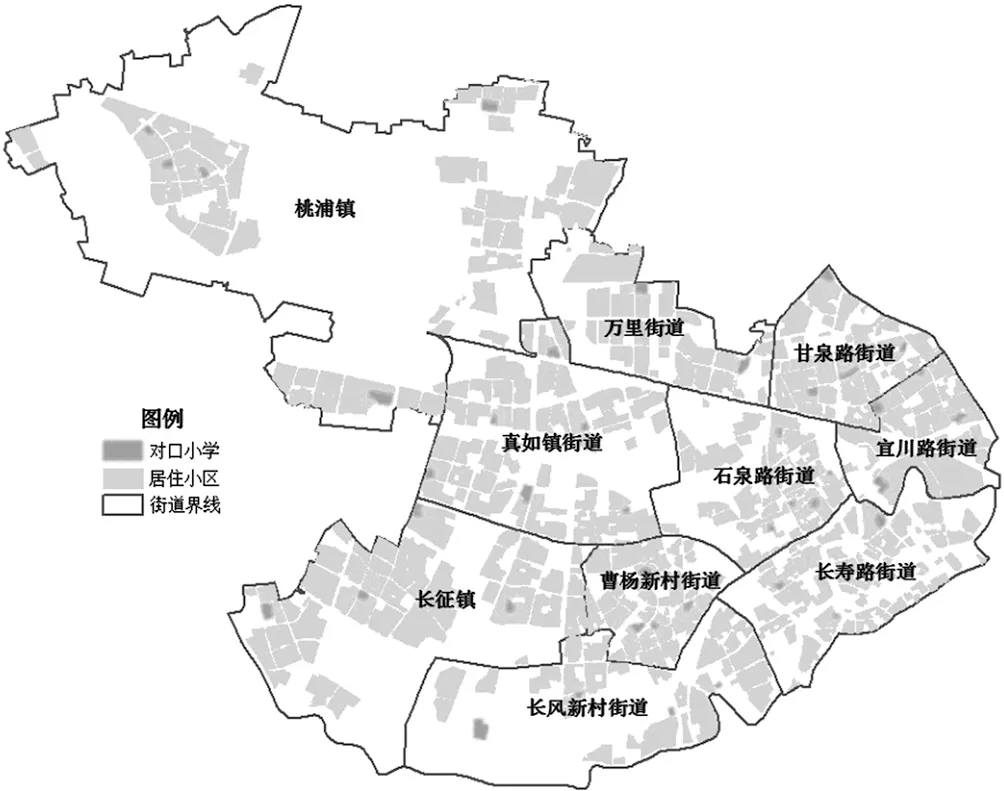
图1 上海市普陀区街道划分图
普陀区的义务教育以公办教育为主,区内民办学校数量较少但办学质量较高,能够对优质公办教育的短缺提供很好的补充。全区教育资源分布不均衡,优质教育资源集中分布在宜川路街道、甘泉路街道等东部地区,这些街道有着较好的教育基础。而西部的桃浦镇、长征镇等地区属于城乡接合部,加之大量的人口导入,教育资源比较紧张。总体来看,全区有限的优质教育资源存量与不断增长的优质教育需求之间的矛盾较为突出[6]。
2.2 小区与学校距离确定
研究小学教育资源空间布局的合理性,实现小学可达性的量化评价,必然是以小学至居住小区的交通距离为基础的,而当前常用的距离多为欧式距离与路网距离,可较简单地获得对应数据,但是与实际的出行距离相差较大,并且只能据此估算出行时间。
本文选择网络交通大数据爬取的方法,获取步行方式的出行距离(m)与出行时间(min),利用真实的出行距离与时间,完成小学可达性的量化评价。
3 小区小学对口关系确定
与医疗、体育、文化、经济等的可达性评价不同的是,教育有公办学校学区划分,即教育局公布招生地段表,对小区居民对口哪所公办学校有十分明确的规定。
“学区制”是义务教育均衡发展体制和机制创新的实践模式之一,是中小学实行分片划区管理的制度。在学区内通过一定的管理制度、运行机制及考核评估措施,搭建交互平台,实现资源共享,实施优质学校对薄弱学校在学校管理和教育教学上的指导与帮扶,以及教育设施设备、师资和生源的均衡分配,从而缩小区域内学校间的差距。这是一种中心拉动、以强带弱、共同发展、整体推进的均衡发展策略。
因此对普陀区小学的可达性进行评价,必然是在保证其对口关系的基础上进行的。即确定小区与小学的对应关系,一个小区对应一所公办小学。在地图中用连接线表示,如图2所示。

图2 普陀区小区小学对口关系图
4 小学教育资源可达性分析方法
4.1 基于交通大数据的最近距离法
可达性评价方法中最简单的方法是最近距离法,就是以两点间的距离为可达性指标,常用来计算所谓的“相对可达性”(lngram,1971)。最近距离模型主要是针对学生的就近入学距离进行比较,离最近设施点越近就代表可达性越好。该模型的数学公式为:
(1)
式中的D表示小学与居民点之间的距离;P表示国家标准规定,小学的服务半径不宜超过 500 m。当比值大于1时,表示小区至小学的可达性不符合国家标准规定,比值小于等于1则表示可达性符合国家标准规定,空间布局相对合理。比值越小,可达性越好[7,8]。
4.2 结合重力模型的两步移动搜索法
采用具有距离衰减系数的结合重力模型的两步移动搜索法(G2SFCA),从小区的尺度对普陀区小学进行可达性计算。考虑距离衰减作用,并将空间上供需双方的空间效应随距离衰减与供需双方自身的引力规模结合起来衡量可达性水平,能更为全面准确地衡量居民获取小学服务的难易程度[9]。
结合重力模型的两步移动搜索法具体如下:
第一步,计算供需比R:
(2)
式中Rj为供需比,表示潜在人均小学服务能力;i为需求点(小区),j为供给点(学校);Sj为供给点的服务能力。Di为需求点的规模;k为搜索半径内居住区地块的数量;dij为需求点i与供给点j之间的距离;d0为搜索半径;G(dij)为考虑到空间摩擦因素的距离衰减函数,计算公式如下:
(3)
第二步,计算可达性:
(4)
式中,αi为每个小区的可达性值;m为落在以i为核心,搜索半径为d0的空间作用域内的学校数量;Rj为第一步计算的供需比。
4.3 熵权法确定学校得分
模型中的供给点(学校)通常选择学生数、教师数等单一性指标来表征学校服务能力,以此判断“供方”对“需方”的潜能大小,而学校服务能力通常是涉及多种因素的综合表现[10~12],因此本文中通过熵权法综合学校各项指标得出综合学校得分,作为学校自身的吸引力。选择在校生数、毕业生数、招生数、班级数、教职工数、专任教师数、占地面积、校舍面积8个指标计算学校得分。
5 实验与结果分析
5.1 基于交通大数据的最近距离法实验结果
本文选择网络交通大数据代替欧氏距离,更加精准地反映可达性实际情况[13]。
《2017普陀区公办小学招生地段范围》中普陀区有对口信息的小学共41个。根据《2017普陀区公办小学招生地段范围》获得小区与小学的对口关系,得到小区至对口小学的交通距离,基于交通大数据的最近距离法实验结果如图3所示:
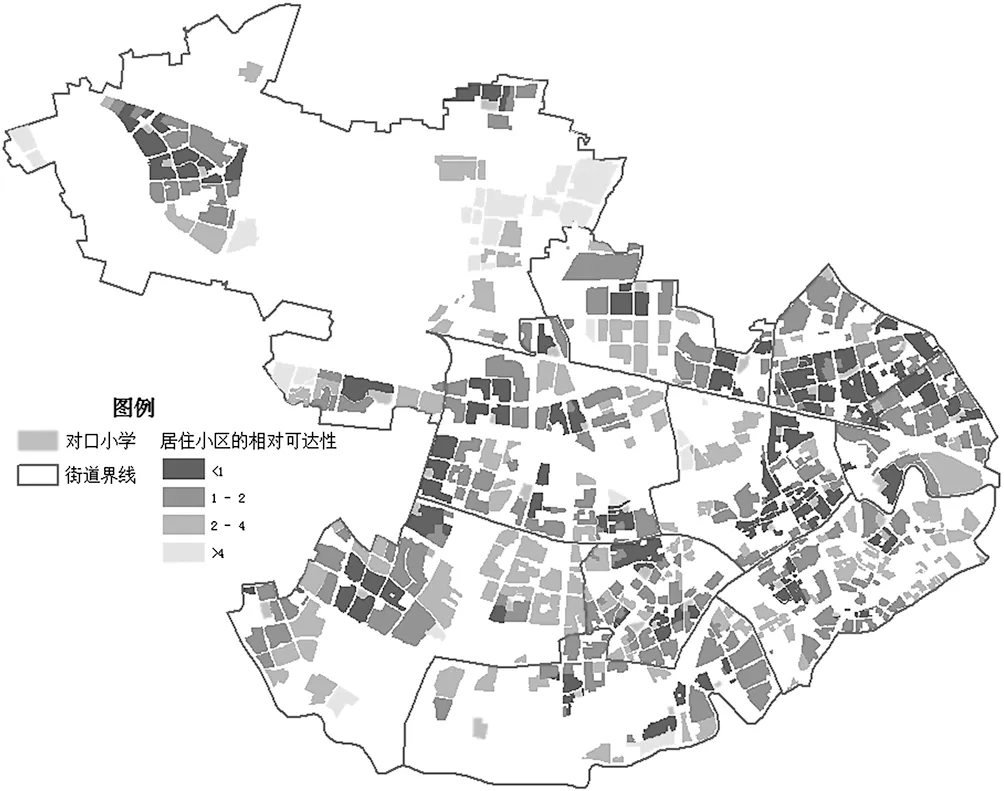
图3 基于交通大数据的最近距离法相对可达性
普陀区小区共674个,其中符合国家规定,即至对口小学距离小于 500 m的小区共160个,占普陀区小区总数的23.7%。至对口小学距离小于 1 000 m的小区共429个,占普陀区小区总数的66.3%。
相对可达性数值越小,小区对应可达性越好。总体上看,普陀区相对可达性东高西低,与普陀区小区和学校东部密集的现状一致。甘泉路街道与曹杨新村街道可达性整体较好,学生上学距离较近。
5.2 结合重力模型的两步移动搜索法实验结果
与传统方法不同的是,由于上海的公办小学存在学区划分规则,按照居住小区分配不同学校,故原定以 500 m为搜索半径计算供需比的方法,改为以对口信息为依据计算各小学供需比,即该小学对口的所有小区。
计算居住小区的空间可达性时,将原定的计算搜索半径内所有小学对该小区的供需比与距离衰减函数乘积的和,改为计算该小区对口小学的供需比与距离衰减函数的乘积。
熵权法确定学校得分结果如表1所示:
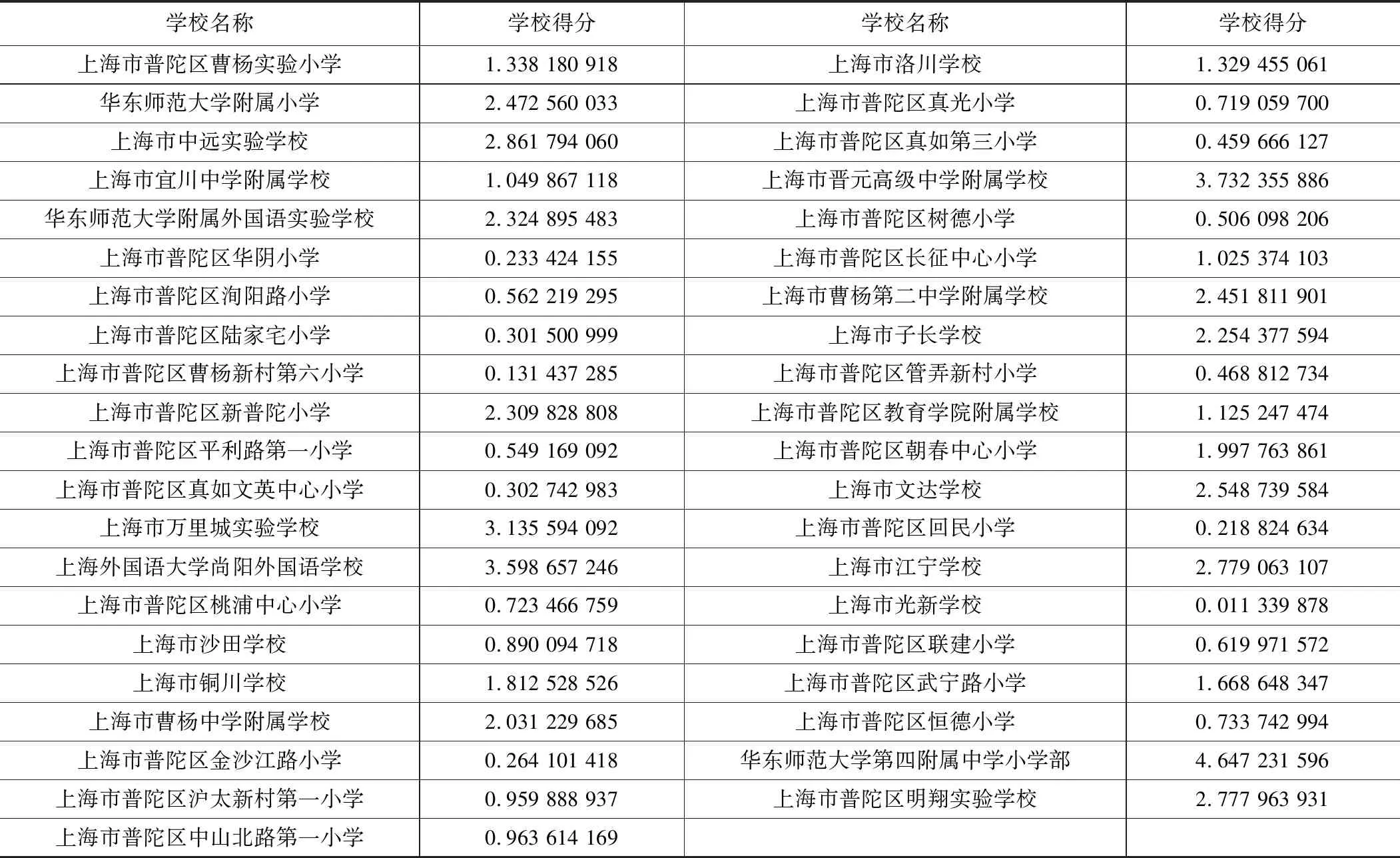
熵权法学校得分结果 表1
因此,结合对口信息与小区人口数据,可得小学供需比如表2所示:

学校供需比结果 表2
华东师范大学第四附属中学小学部供需比比其他学校高很多,探究其原因,是该学校仅对口一个居委,且居委内小区适龄儿童人数极少(人口数据为2010年第6次人口普查数据,故可能时效性较低)。
计算得居住小区的空间可达性如图4所示:
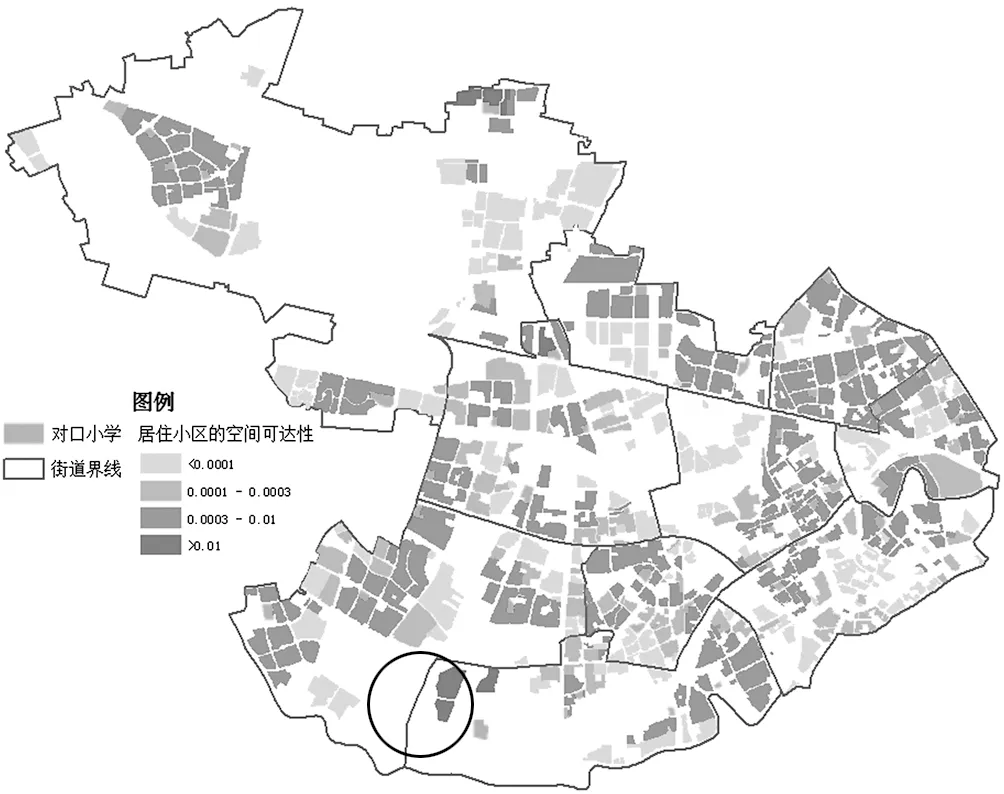
图4 结合重力模型的两步移动搜索法空间可达性
根据结合距离衰减函数的空间可达性来看,在普陀区各小区至小学的可达性差异较大,华东师范大学第四附属中学小学部(橘色圈内)供需比比其他学校高很多,因此,在结合距离衰减函数的空间可达性研究结果中,该学校对口的小区可达性均属于最高水平。从图4中可以看出,甘泉路街道可达性均较高,长寿路街道部分区域与桃浦镇部分区域可达性相对较低。
5.3 实验对比
基于交通大数据的最近距离法实验结果与结合距离衰减函数的小学空间可达性研究结果,有相似也有不同。
共同点是,两个实验结果中可达性整体趋势相似,上海市普陀区可达性东高西低,与普陀区小区和学校东部密集的现状一致,甘泉路的可达性均较好,长寿路的可达性均相对较差。
区别是,部分学校如华东师范大学第四附属中学小学部等的周边小区,由于考虑供需比,即学校的得分与小区适龄儿童人数等,表现出与最近距离法不同的趋势,更加精准地反映各小区可获得的小学教育资源现状。
6 基于Huff模型的小学学区划分优化方法
常用的Huff模型能够计算出每个居民点到小学的可达性概率、小学对居民点的吸引力、潜在师生比、以及潜在服务学生数等,并对学校的服务区进行划分,得到每个居民点学生就学的难易程度以及各小学拥有教育资源差异。Huff模型能够较好地模拟出各个居民点上的学生在选择不同学校时的不同入学概率,从而为学校的学区划分提供客观的依据。
在规划布局已定的情况下,本研究旨在考虑如何通过合理的服务区划分使得教育资源分配更均衡。如果一个社区的居民到某个小学就学的概率最高,意味着这个社区与该小学的相互作用最强,因此可以将这个小区划到该小学的学区范围。实现方式如下:
(1)根据网络交通大数据,获得普陀区各居住小区分别至所有普陀区内小学(含一贯制学校)的距离。
(2)计算每个小学对各个小区的吸引力
(5)
(6)
其中,Aij表示第j个小学对第i个居住小区的吸引力,Pij为第i个居住小区到第j个小学上学的概率。Sj为第j个小学的学校质量,dij为第i个居住小区到第j个小学上学的距离,即交通成本,β=2[14,15,16]。
(3)根据Pij筛选出对该小区吸引力最大的学校,即根据第i个小区的最大Pij值,j学校作为该小区的建议对口学校,从而确定基于Huff模型的小学学区对口关系。
7 基于Huff模型的小学学区划分优化实验结果
通过基于Huff模型的小学学区划分优化实验,获得建议优化后的普陀区小学对口关系,如图5所示,本文中Sj选择5.2中熵权法学校得分来表示第j个小学的学校质量。

图5 普陀区小区小学优化后对口关系图
将图2与图5相对比,优化前与优化后对口关系发生了较大变化,根据网络交通大数据,对优化前后学生入学距离进行对比分析,分析结果如表3所示:

优化前后学生入学距离对比 表3
对优化前后情况进行比较。结果显示,优化后,所有小区到对应学校的距离总和由 621 255 m缩短至 598 429 km,整体优化幅度达3.6%;上学的最远距离由 4 022 m缩短至 2 754 m,减少了31.5%;上学平均距离由 922 m缩短至 888 m,减少了3.7%;位于国家标准建议的小学 500 m服务范围内的小区占比由23.7%增长至25.4%,增长了7%。
因此结合HUFF模型,筛选出对每个居住小区吸引力最大的小学,确定新的学区优化配置,从空间上看,对学生入学可以起到一定的优化作用,该方法可以为政府有关部门学区划分决策提供可靠建议。
8 结 语
本文结合上海市公办学校学区划分的现状特征,在传统的教育资源可达性计算的基础上,提出按照学区划分判断可达性的改进方法,即基于交通大数据的最近距离法与结合距离衰减函数的小学空间可达性计算方法,分别对上海市普陀区小学教育资源现状与小区可达性进行评价,并对两种方法进行比较。为相关部门进行选址规划以及教育资源均等化配置等方面提供了有力的技术支撑。除此之外,本文在网络交通大数据与学校得分的基础上,通过Huff模型,对上海市普陀区的学区划分进行优化,对比分析现状与优化后学生入学距离,对优化结果进行客观评价,为今后教育部门的学区划分工作提供参考。但是,仍有部分内容,如熵权法计算结果作为供方服务能力是否需改进、实验结果是否与普陀区各街道经济发展水平等保持一致等等,有待进一步探究。
