基于机理模型和模糊加权最小二乘支持向量机(LSSVM)算法的农杆菌发酵过程混合建模与优化

邵玉倩，宗原，刘以安，刘登峰*

1(江南大学 物联网工程学院，江苏 无锡,214122) 2(轻工过程控制教育部重点实验室(江南大学)，江苏 无锡，214122)

热凝胶多糖是农杆菌(Agrobacteriumsp.) ATCC31749发酵产生的一种重要的高分子量均一线性胞外多糖[1]，因其特有的凝胶功能，在食品和制药行业具有十分广泛的应用。随着凝胶多糖在生物医学中应用的重要性日益提高，专家们一直致力于通过提高发酵效价来降低凝胶多糖的生产成本。目前在发酵过程中已经提出了多种策略来提高发酵效价：(1)控制pH值。如LEE等[2]通过控制pH值以遵循最佳分布，并通过反馈最优控制实现凝胶多糖产量的最大化；(2)构建基因工程菌株。如SHIN等[3]使用强有力的启动子和工程菌株将纤维二糖高效地转化为凝胶多糖，以及YU等[4]证实，crdR可通过激活其生物合成基因的表达来调节凝胶多糖合成；(3)添加辅因子和更换廉价底物。如WEST等通过以浓缩玉米蒸馏液为底物[5]和添加嘧啶碱[6]来提高凝胶多糖的产量。

新近研究表明，在热凝胶发酵过程中，溶氧浓度(dissolved oxygen tension, DOT)不仅影响细胞生长速率、死亡速率而且对产物凝胶多糖和副产物合成均有重要影响[1]。因此，如何选择合适的溶氧过程控制已经成为强化凝胶多糖产物合成的关键途径之一，而建立以溶氧为输入变量的高精度热凝胶发酵控制模型，对指导以实现产物最大化的溶氧过程控制优化具有重要的意义。因此，建立基于溶氧浓度为关键输入变量的高精度发酵产物浓度预测模型亟需进行研究。

发酵模型分为白箱模型、黑箱模型和灰箱模型。白箱模型(即机理模型)[7-12]能够清楚地反映出发酵过程中生物量与一些辅助变量之间的关系，展现出发酵过程的主要框架，但模型精度不高。黑箱模型(即经验模型)[13-18]根据对象的输入输出数据，利用智能计算方法直接建模，结构简单，非线性拟合能力强，但由于黑箱模型不考虑发酵过程机理知识，过于依赖训练数据，容易造成模型过拟合，且模型泛化能力弱，不具有可解释性。为了克服这些缺点，灰箱模型应运而生。灰箱模型(即混合模型)是结合了机理模型和经验模型的优点而建立的模型。GHOVVATI等[19]用遗传算法和粒子群算法进行混合来估计动力学模型中的参数，董亚明[20]基于双神经网络与机理模型混联建立了发酵过程混合模型，桑海峰[21]、黎兴宝等[22]均是基于机理知识和最小二乘支持向量机建立了混合发酵模型。

而在农杆菌发酵法产凝胶多糖的溶氧优化方面，ZHANG等[1]在Logistic方程和Luedeking-Piret方程的基础上用Runge-Kutta法来求解动力学模型，并用遗传算法来寻找模型参数，根据模型参数与溶氧浓度的关系建立以溶氧体积分数预测发酵产物浓度的模型，但是该模型求解方法计算量大，求解精度有待提高。针对该问题，本文在ZHANG等建立的机理模型的基础上，首先通过添加模糊加权思想和混合核函数方法对最小二乘支持向量机(least squares support vector machine, LSSVM)算法进行优化改进；然后用改进的LSSVM算法求解机理模型的动力学方程，实现混合建模；最后对建立的混合模型实现关键控制变量的单一化，并进行了以实现产物浓度最大化为目的的溶氧过程控制曲线优化。

1 材料与方法

1.1 菌株

本文所用的微生物农杆菌(Agrobacteriumsp.) ATCC31749来源于江南大学生物工程学院。

1.2 培养基

实验种子发酵培养基：葡萄糖、酵母浸膏、KH2PO4、MgSO4，pH 7.0～7.2。

分批补料发酵培养基：葡萄糖、酵母提取液、KH2PO4、MgSO4·7H2O、NH4Cl，还包含少量微量元素(NaCl、CaCl2、MnCl2、FeCl3·H2O)。

1.3 培养方法

将500 mL培养瓶中的100 mL种子发酵培养基接种于土壤杆菌(Agrobacteriumsp.) ATCC31749培养物中，初始pH 7.0～7.2，温度为30 ℃，然后在200 r/min振荡18 h。发酵实验在7 L搅拌槽发酵罐中进行，搅拌速率为400 r/min，在细胞生长阶段pH值维持在7.0，当氮被消耗完时调整pH值为5.5，温度为30 ℃。

1.4 不同溶氧浓度下菌株发酵

在发酵过程中通过使用氧电极的方式分别控制溶氧体积分数维持在15%，30%，45%，60%和75%并分批做实验，实验环境与1.3中相同。

2 发酵产物浓度预测的混合建模

为从溶氧控制角度优化发酵过程，实现提高凝胶多糖产量和降低生产成本，本文针对文献[1]中模型精度不高的问题，采用融合建模策略，来实现高精度预测模型的建立。总体思路是首先建立机理模型，在文中为微分方程组，然后将微分方程作为LSSVM的约束方程求出生物量浓度、氮浓度、葡萄糖浓度和多糖产量随时间变化的情况。分别用溶氧体积分数为15%、30%、45%、60%和75%的实验数据进行训练，用鸟群算法寻找不同溶氧体积分数下的最优参数值，分析出溶氧体积分数与模型参数之间的关系，然后用溶氧体积分数作为输入变量建立由溶氧体积分数预测发酵产物浓度的模型，最后用鸟群算法寻找最优溶氧体积分数，使得多糖产物浓度最大(图1)。

图1 混合模型结构流程图

Fig.1 Mixed model structure flow chart

2.1 机理模型

农杆菌ATCC31749发酵合成凝胶多糖只有在限氮的条件下才会进行[1]，因此，在农杆菌的发酵过程中，在热凝胶合成阶段，由于缺乏氮源，细胞的生长受到抑制，葡萄糖主要用来合成多糖和维持细胞正常的代谢。所以文中机理模型包括了氮源浓度、葡萄糖浓度、生物量浓度以及多糖产物浓度在发酵过程中随时间变化的关系(参数意义见表1)。

表1 模型参数意义

文中机理模型是在两个假设的基础上构建的：(1)氮源是细胞生长过程中的限制性底物；(2)葡萄糖用于细胞生长、细胞维持和多糖生物合成。

生物量浓度、氮源浓度、葡萄糖浓度以及多糖产量浓度在发酵过程中的变化简述如公式(1)～(4)[1]：

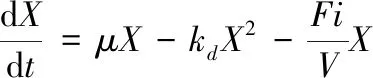
(1)

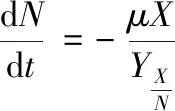
(2)

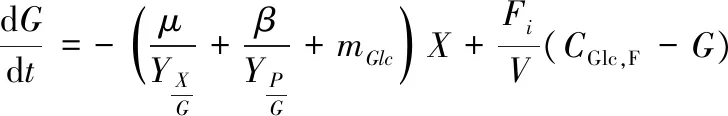
(3)

(4)

其中的动力学参数表示如下：

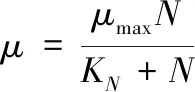
(5)

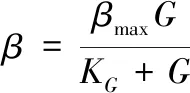
(6)

2.2 LSSVM的混合核函数

对LSSVM而言，采用不同的核函数所建立的LSSVM的性能是不同的，因此核函数的选择至关重要。核函数的主要种类为：

线性核函数：K(x,xi)=xTxi;

多项式核函数：K(x,xi)=(γxTxi+r)p,γ>0;

σ>0;

Sigmod核函数：K(x,xi)=tanh(γxTxi+r),γ>0,r>0;

根据核函数的特征，可以将核函数分为局部核函数和全局核函数[23-25]。局部核函数的局部学习能力较强，即局部核函数对距离测试点周围小范围的数据影响较大，全局核函数则相反。由文献[23-25]可知，上述核函数中多项式核函数属于全局核函数，径向基核函数属于局部核函数，且基本核函数的线性组合仍为核函数，因此，本文采取的核函数为多项式核函数与径向基核函数的线性组合。

ε∈[0,1]σ>0,γ>0

(7)

对上述核函数求偏导可得：

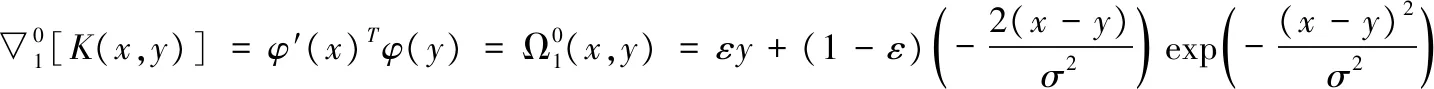
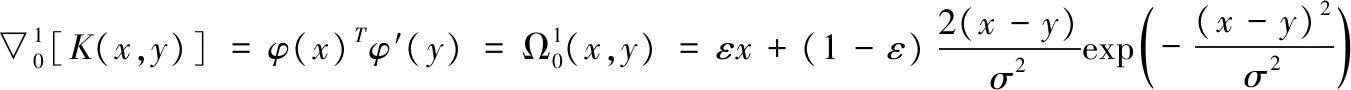
2.3 模糊加权LSSVM求解动力学模型

由于发酵过程的复杂性和不确定性，不同时期的实验数据对模型建立的重要性是不同的，因此，本文在模型训练时对每个样本加入模糊加权隶属度μi[26]。对于文中一阶非线性常微分方程，在LSSVM框架下，可将微分方程转化为如下的优化问题，以式(1)为例，将式(1)作为LSSVM的约束条件进行计算，具体如下：

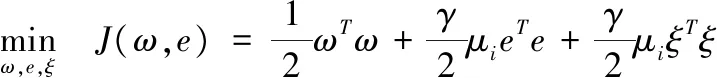
s.t.ωTφ′(ti)+b1=f(ti,yi)+ei,i=1,2,kN,

(8)

ωTφ(t1)+b1t1+b=p1,

ωTφ(ti)+b1t1+b+ξi=yi,i=1,2,kN.

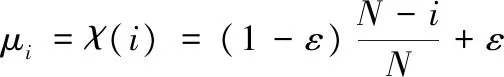
(9)

建立拉格朗日函数如下：

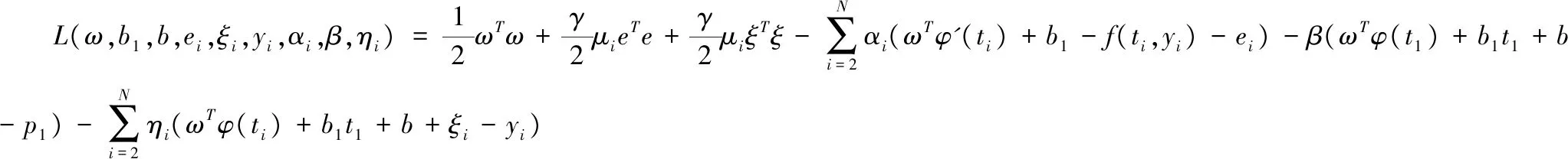
由KKT条件可得：

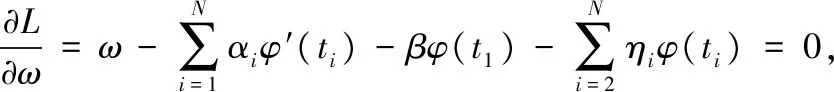
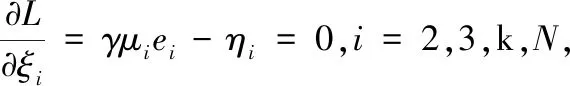
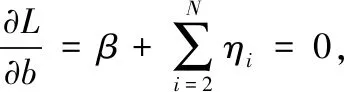
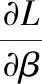
消去ω、ei和ξi后，整理以上公式如下：

(10)

建立拉格朗日函数如下：

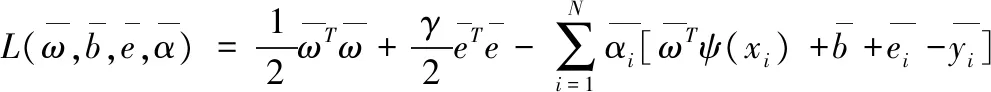
(11)

(12)

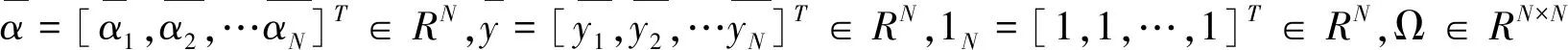
通过解上式方程组可得原非线性常微分方程初值问题的近似解，其形式如下：

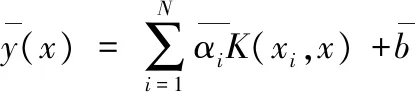
(13)

2.4 鸟群算法寻优

鸟群算法是在2015年由MENG等提出的模仿自然界鸟群觅食、警戒和飞行行为的群智能算法[27-28]，具有寻优精度高,鲁棒性好等优点。

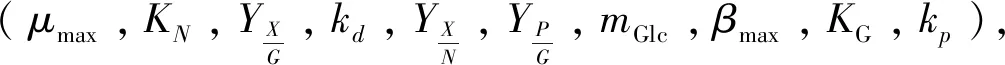
3 实验仿真、评估与应用

3.1 农杆菌发酵实验与仿真

在不同溶氧体积分数下得到的X、N、G和P的预测值，并与1.4中的实验值进行比较，用误差平方和来衡量预测精度，具体公式如下：

Zall=ZX+ZN+ZG+ZP

(14)

式(14)中：Xi,exp、Ni,exp、Gi,exp以及Pi,exp分别代表农杆菌ATCC 31749发酵过程中生物量浓度、氮浓度、葡萄糖浓度和多糖产量浓度的实验值，而Xi,sim、Ni,sim、Gi,sim及Pi,sim分别代表动力学模型对生物量浓度、氮浓度、葡萄糖浓度和多糖产量浓度的预测值。将文中模型预测结果与ZHANG等的实验结果进行对比，实验结果如图2～图6所示。表2为2种模型的仿真误差对比(模型1是文献[1]中模型，模型2是本文混合模型)。

从图2～图6的实验仿真结果中可以看出：在不同溶氧体积分数下，文中混合模型即模型2对生物量、氮、葡萄糖和凝胶多糖质量浓度的预测值均更贴近实验值。2种模型的误差对比如表2所示，从表2中可以看出，本文中建立的混合模型2，其预测误差平方和比文献[1]中误差平方和的平均值降低了40%。因此，本文中建立的混合模型与已有模型相比，其仿真精度更高。

图2 15%DOT时各参数预测图

Fig.2 Prediction of each parameter at 15% DOT

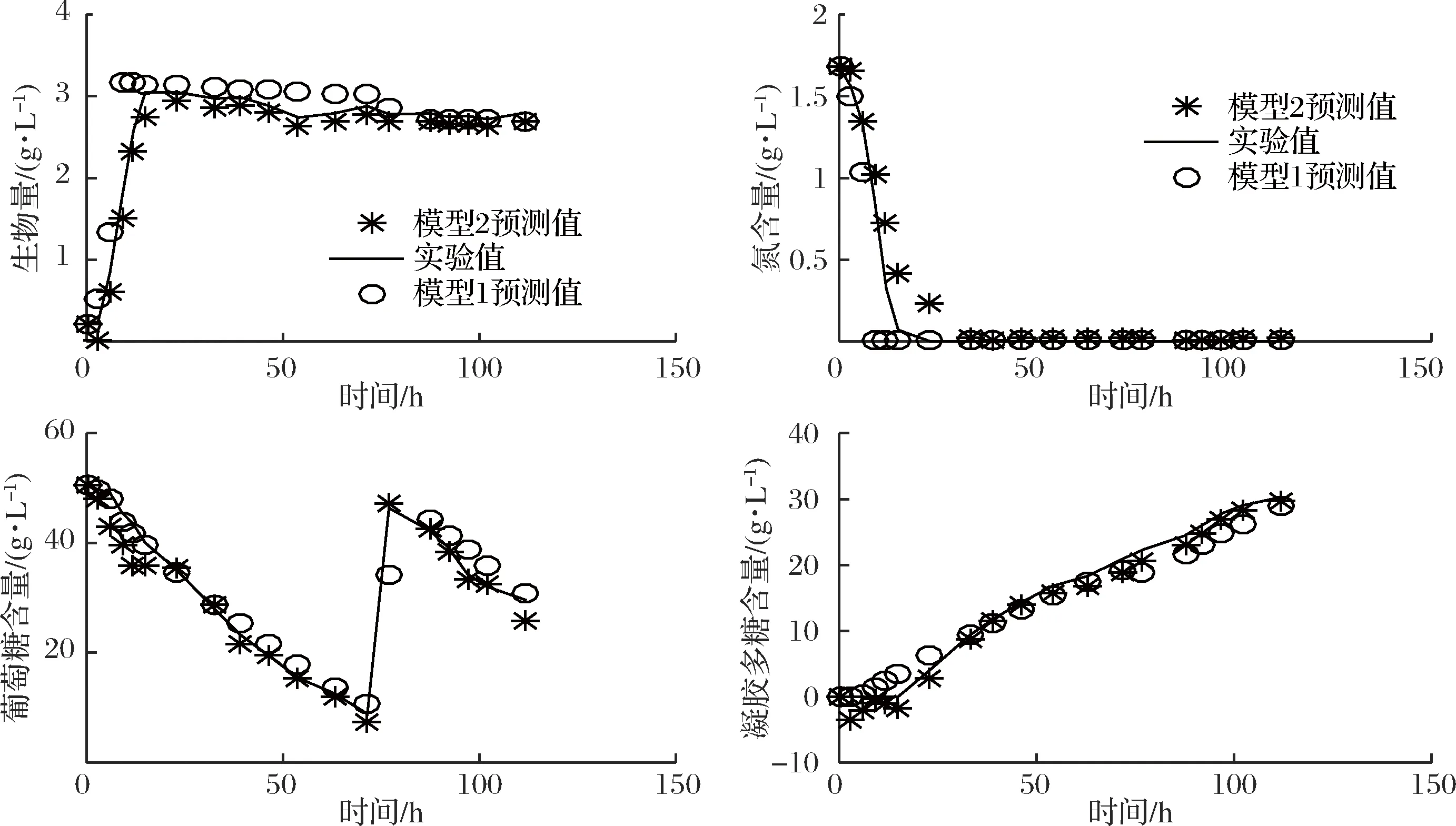
图3 30%DOT时各参数预测图

Fig.3 Prediction of each parameter at 30% DOT

表2 两种模型误差对比

3.2 不同溶氧浓度下模型仿真中的参数取值

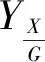
图4 45%DOT时各参数预测图

Fig.4 Prediction of each parameter at 45% DOT

图5 60%DOT时各参数预测图

Fig.5 Prediction of each parameter at 60% DOT

表3 不同溶氧浓度下的模型参数取值

Table 3 Values of model parameters under different dissolved oxygen concentration

参数DOT(15%)DOT(30%)DOT(45%)DOT(60%)DOT(75%)μmax/h-10.285 00.284 80.284 4 0.285 00.285 0KN/(g·L-1)0.018 40.018 50.018 50.018 50.018 2kd/[L·(g·h)-1]2.098 7×10-42.152 8×10-42.847 5×10-42.954 9×10-43.264 0×10-4YXN/(g·g-1)1.684 51.709 71.751 01.882 61.778 5YXG/(g·g-1)0.400 00.400 60.400 00.432 00.400 0YPG/(g·g-1)0.596 80.686 10.745 70.799 10.562 5mGlc/[g·(g·h)-1]0.073 90.024 40.013 20.005 00.033 1 βmax/(g·g-1)0.108 80.200 30.224 80.247 90.100 0 KG/(g·L-1)19.164 3 20.511 620.279 521.591 620.570 7kp/(g·L-1)2.516 9×10-42.800 0×10-43.615 1×10-45.957 1×10-41.813 3×10-4

3.3 获取溶氧优化控制曲线

在得到溶氧体积分数和主要模型参数之间的函数关系后，用溶氧体积分数代替模型参数进行计算，从而建立起了由溶氧体积分数预测发酵产物浓度的混合模型。表5中列出了文献[1]中模型在不同溶氧体积分数下的凝胶多糖产物体积分数的仿真预测值，混合模型的仿真预测值和实验值。

图6 75%DOT时各参数预测图

Fig.6 Prediction of each parameter at 75% DOT

表4 溶氧浓度与各模型参数的关系

Table 4 Relationship between dissolved oxygen concentration and various model parameters

模型参数模型参数与溶氧浓度的关系kd-1.083 7×10-9×O3+1.438 5×10-7×O2-3.445 1×10-6×O+0.000 229 96YXN-6.217 3×10-6×O3+7.859×10-4×O2-0.025 799×O+1.921 4YPG-2.669 1×10-6×O3+2.866 8×10-4×O2-0.007 545 9×O+0.582 32mGlc2.711 1×10-5×O2-0.002 628×O+0.115 3βmax-2.567 9×10-6×O3+1.942 2×10-4×O2+0.000 284 44×O+0.072 86KG-1.860 7×10-5×O3+0.001 498 6×O2+0.018 352×O+18.714 6kp-1.732 8×10-8×O3+2.106 7×10-6×O2-6.991 1×10-5×O+0.000 897 7

表5 不同溶氧浓度下各模型多糖产物浓度预测值与实验值

从表5中可以看出,2种模型都能通过溶氧体积分数预测出凝胶多糖产物浓度且2种模型的最优溶氧均为52%，但是模型1的预测值与实验值相差在3左右，而本文所建立的以溶氧为控制参数的模型2与实验值相差仅1左右。因此，模型1的预测精度小于本文所建立的混合模型的预测精度。

在农杆菌发酵工业中，如何通过控制溶氧来实现目的产物的最大化，是农杆菌发酵控制策略开发的主要任务之一。因此，以混合模型为基础，进行了以实现凝胶多糖产量最大化为目的的最优溶氧过程控制策略预测，结果如图7、图8所示。在图7所示的溶氧控制模式下，模型仿真的凝胶多糖的产物质量浓度为48.85 g/L(图8-d)。

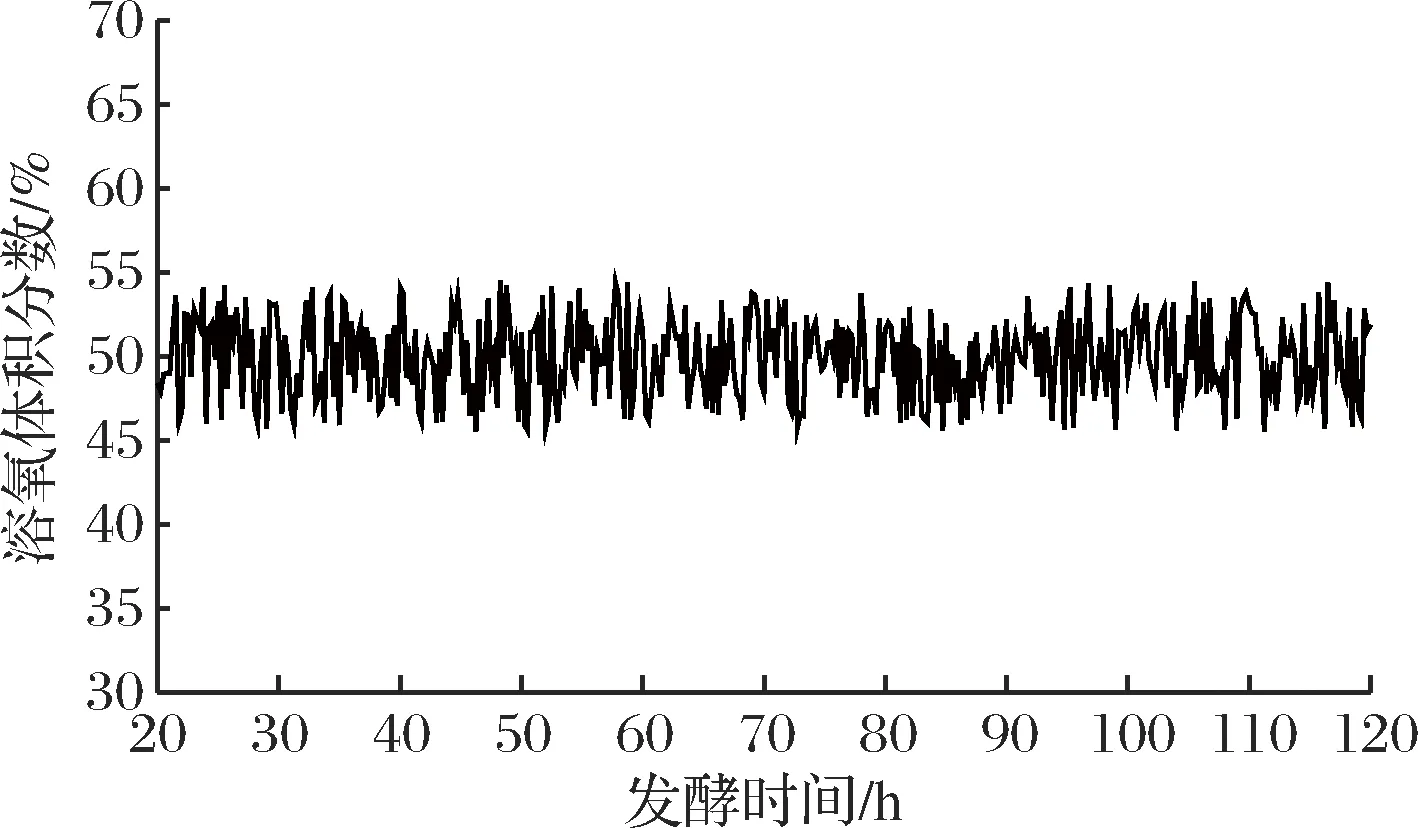
图7 溶氧过程控制图

Fig.7 Dissolved oxygen process control chart

4 结论

本文使用优化后的LSSVM对动力学模型进行估计来提高预测精度。建立了以溶氧体积分数为输入控制量的发酵产物浓度混合预测模型。从文中实验仿真结果中可以看出，LSSVM求解的动力学模型精度比传统的数值解法的误差平均降低40%，以LSSVM为基础的混合模型的预测精度约提高2，因此文中混合模型的建立是有效的，模型预测精度更高。最后用鸟群算法找到使得多糖产物质量浓度最大(48.85 g/L)的最优溶氧体积分数(52%)。该混合模型为进一步通过溶氧优化控制来提高多糖发酵产量提供了新的方向。

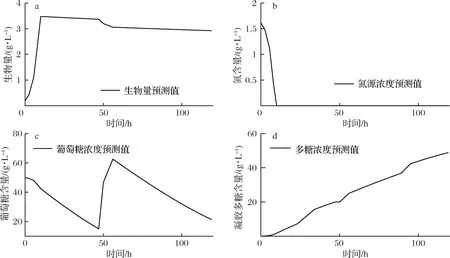
图8 最优溶氧时各参数值

Fig.8 Parameter value of optimal dissolved oxygen concentration