一种机载GNSS高精度定位算法

符彦

(广东省地质测绘院,广东 广州 510800)

0 引 言

全球卫星导航系统(GNSS)航空测量不受地形限制、作业效率高,可广泛应用于大地测量、地形测绘等领域．基于GNSS观测值精确求解载体的位置是航空测量的关键[1]．长距离实时动态定位(RTK)、精密单点定位(PPP)、网络RTK等是目前实现GNSS航空动态定位的主要手段,在摄影测量、航空重力、机载InSAR及水深测量等领域得到广泛应用[2-7]．文献[8]提出.基于PPP技术求解高精度动态定位解,但无法固定整数模糊度,精度低于差分模式;文献[9]分析了GNSS航空动态定位主要误差源及其影响,表明电离层延迟误差的处理是高精度动态定位的关键;文献[10]采用网络参考站改善单参考站GNSS航空测量定位的效果;文献[11]提出自适应换站的思想融合不同参考站观测信息从而保持长距离动态定位的高精度与连续性．文献[10-11]的两种方法都是充分利用多个基站的观测值提高动态定位精度;本文则利用电离层延迟误差随着基站距离变化的规律构建虚拟观测量提高定位精度．

受成本、地形等因素制约,GNSS航空测量常依赖于长基线相对定位,然而,目前存在以下几方面问题:采用无电离层模型,需积累较长时间观测数据以实现首次模糊度固定;另外,GNSS航空测量基线长度不断变化,当基线较短时,仍采用长基线定位模型影响基线解算的效率、精度与可靠性,而长、短基线定位模式之间的切换实现过程较为复杂,实际可行性较差．为此,本文提出两项措施以解决上述问题:首先,采用加权电离层模型代替无电离层模型,在顾及双差大气延迟随基线长度变化基础上,引入距离加权的双差电离层“虚拟”观测量,提高模型强度与浮点解质量;其次,为充分挖掘模糊度参数的整周约束信息,当模型无法可靠地固定全部模糊度时,选用部分模糊度固定策略,提高模糊度固定效率及可靠性．本文方法可自适应调整大气扰动随时间、空间的变化,实现长短基线定位模式的灵活、有效切换,而部分模糊度固定策略充分发掘了模糊度参数的整周特性．

1 GNSS定位模型

1.1 浮点电离层模型

GNSS动态定位非组合双差观测方程为

(1)

1.2 无电离层组合模型

对于双频GNSS接收机,通常采用双频无电离层组合模型消去电离层延迟:

(2)

图1 无电离层模型数据处理流程

式中:几何无关、电离层无关观测值MwIF=(f1P1+f2P2)/(f1+f2)-(f1Φ1-f2Φ2)/(f1-f2),波长λIF≈0.63 cm．无电离层模型消去n个电离层延迟参数的同时减少了n个独立观测量,模型保留了与位置、对流层、模糊有关观测信息,但损失了与电离层有关的有效观测信息[12](如图1所示)．实际应用中将式(2)简化处理,MW观测值仅用于宽巷模糊度固定,而模糊度浮点解仅由组合观测值ΦIF、PIF计算．无电离层模型数据处理流程如图1所示:固定宽巷模糊度后,将其视为确定性整数代入无电离层模糊度从而分离宽巷与窄巷模糊度;参数分离后,窄巷模糊度波长为λIF的17倍(约11.7 cm),由此得到窄巷模糊度浮点解及协方差阵进行模糊度固定．

1.3 加权电离层模型

航空动态测量中往往需要大范围内作业,动态基线长度变化范围一般为几千米至几百千米,通常需要根据经验判定的短/长基线长度确定对应的定位模式．短/长基线模式的差异在于对大气延迟的数学约束方式不同．为避免该经验性判定的不可靠性,一种有效的策略为引入“虚拟”观测值描述双差大气延迟残差．

引入双差电离层虚拟观测方程如下:

ι0=ι+ει0，

(3)

式中:ει0为随机噪声;虚拟电离层观测量ι0可来自外部电离层模型,如GIM模型或区域电离层延迟模型,也可以简单地假设双差电离层延迟为小量(接近于0)．双差虚拟电离层延迟协方差阵可由站间单差斜电离层延迟协方差阵计算:

(4)

式中:σι0为非差斜电离层延迟投影至穿刺点处垂直方向虚拟观测值单位权中误差;Λ为单差斜向电离层延迟协因数阵,由穿刺点(站星视线与薄层交点)处斜延迟投影函数描述．随机噪声σι0的准确描述极其重要:若随机噪声取值过小,如σι0→0,此时模型退化为忽略电离层延迟的短基线RTK模型,对于长基线动态定位或导致参数估值有偏,影响模糊度解算效率及定位精度;若随机噪声取值过大,如σι0→∞,模型退化为与无电离层模型等价的“浮点”电离层模型,此时模型牺牲了计算效率却没有达到提高模型强度的效果．考虑双差电离层残差与基线长度密切相关,假设“虚拟”电离层观测量精度(中误差)基线长度成正比:

(5)

取s0=100 km,由基线长度s与σs0/s0共同给定虚拟电离层观测值的加权精度,s单位为km,σs0/s0单位为cm/100 km．

后处理模式下,动态基线分量与电离层延迟视为与历元相关的未知参数,天顶对流层延迟则可被描述为分段线性函数[13],时间分辨率可调节为由数小时提高为3 min,以适应航空动态中环境变化．为避免参数过多降低模型强度,采用文献[13]中的方法对相邻节点间的天顶对流层延迟施加动态约束:

(6)

式中,qτ为随机游走噪声的功率谱密度,其典型值为4 cm2/h．当基线小于1 km时,引入使得天顶时延近似为0的确定性约束(加权精度为1 mm):

τ0=τ+ετ0.

(7)

加权电离层模型一方面可采用统一模型兼容短基线/长基线定位模式,另一方面可提高长基线动态定位的模型强度,从而提高模糊度固定效率与定位精度及可靠性．加权电离层模型数据处理流程如图2所示,该模型与无电离层模型相比,具有如下特点:

1)非组合模型宽巷模糊度估值为

f2Φ2)/(f1-f2),

(8)

MW是一种无电离层、几何无关组合,无电离层模型MW观测值仅用于模糊度固定,因此加权电离层模型多一个有效观测量,窄巷模糊度浮点解强度更高;

2)无电离层模型损失了电离层参数的信息,而加权电离层模型可灵活应用外部电离层约束或动态约束提高模型强度．

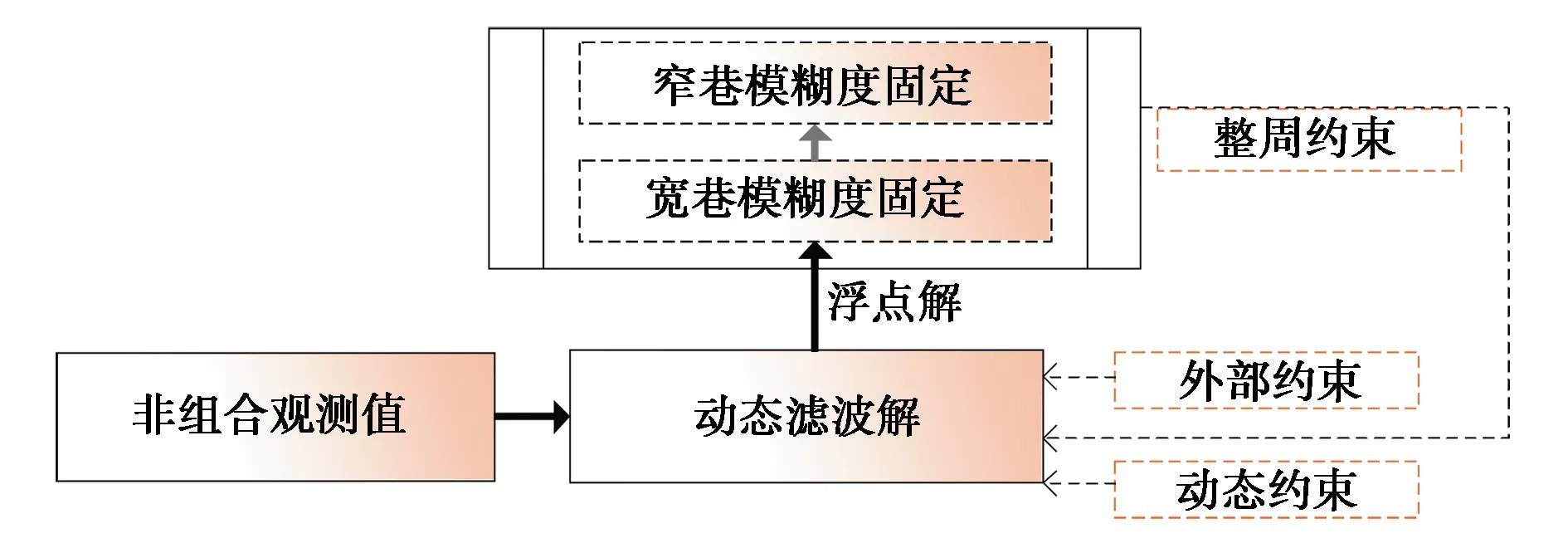
图2 加权电离层模型数据处理流程

2 部分模糊度固定

2.1 宽巷-窄巷序贯固定

(9)

其中,T为转换矩阵．对双频模糊度与宽巷-窄巷组合模糊度的整数最小二乘搜索问题本质上等价．通过式(9)变换,可利用宽巷模糊度波长较长的特点,采用宽巷-窄巷序贯搜索策略提高模糊度固定效率,宽巷模糊度固定约束的窄巷模糊度浮点解为

(10)

2.2 部分模糊度子集选取

受数据质量、模型强度、系统误差多种因素影响,不同模糊度的浮点解质量不尽相同,往往难以可靠地固定全部模糊度,此时传统方法放弃模糊度固定,保持浮点解．简单地固定或不固定所有模糊度有可能大大降低模糊度固定效率．为充分挖掘模糊度的整周约束条件,此时固定部分质量可靠的整周模糊度不妨为一种更有效的策略．部分整周模糊度固定的关键为模糊度子集的选取,通常先利用模糊度降相关算法进行整周变换,在整周变换后的模糊度域选精度较高的模糊度优先固定．模糊度降相关的主要贡献为加快模糊度搜索效率,且在降相关后的模糊度域选取子集具有其局限性,如无法实现部分模糊度初始化(模糊度初始化即将模糊度视为常值代入滤波器),本文在原始模糊度域选择最优模糊度子集．另外,协方差阵无法完全衡量模糊度浮点解的质量好坏,为有效控制纳伪概率,提高整数解的可靠性,采用浮点解精度、偏差、观测时长等交叉准则选取模糊度子集,具体包含以下步骤:

1)为保证实数解的几何强度,数据预处理阶段排除观测时长较短(小于5 min)与低高度角(小于13°)数据弧断;

2)给定小数和方差阀值(FFV),排除精度低于0.2周、小数偏差大于0.4周的模糊度子集;

3)计算剩余模糊度子集的模糊度固定成功概率,若成功概率小于给定阀值(99.99%),从模糊度子集中剔除方差较大的模糊度,直至纳伪概率小于0.01%．

3 实验分析

为客观分析各项改进措施的实际效果,笔者用2011年8月25日进行航空摄影测量采集的GPS数据进行动态定位实验,机身搭载Trimble 5700双频GPS接收机,采样率为1 Hz,飞行时长约2.6 h,飞行轨迹如图3所示,动态基线长度变化如图4所示,飞行过程中跟踪不少于5颗卫星,如图5所示．

图3 飞行平面与高程轨迹图

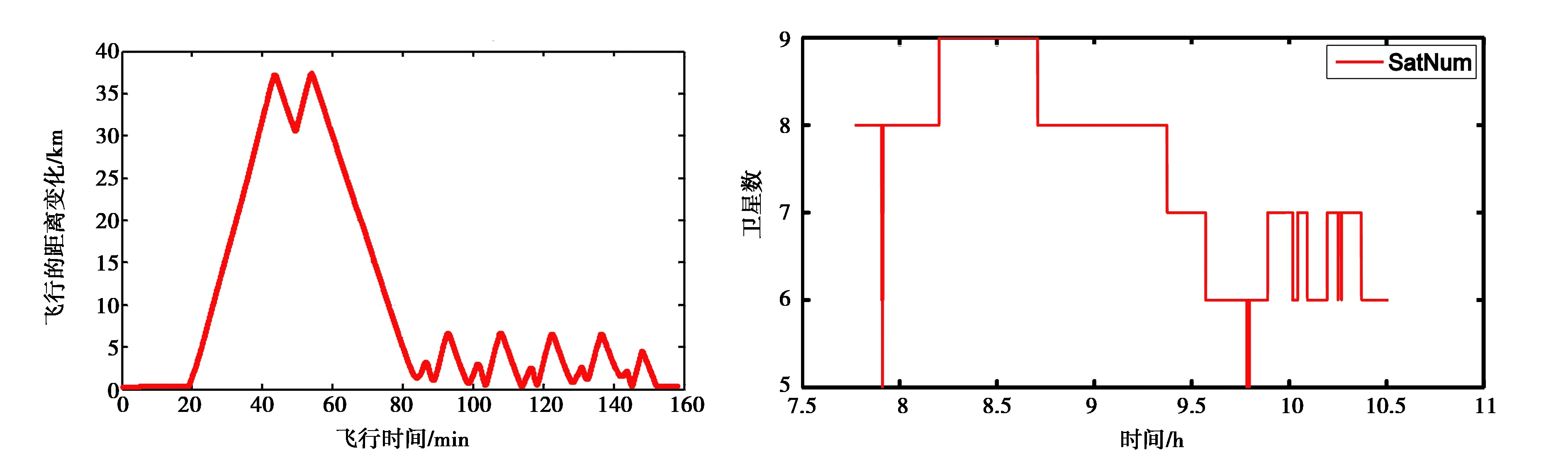
图4 基线长度变化 图5 卫星数

GPS定位解算分为数据预处理、模糊度解算、动态定位三步:1)数据预处理部分包含粗差探测与剔除、周跳探测、接收机钟跳探测与修复、剔除观测连续性较差(低于5 min)或低高度角(低于13°)的观测弧段等;2)采用序贯最小二乘滤波计算模糊度浮点解,而后固定宽巷模糊度,并以宽巷模糊度为约束条件固定窄巷模糊度;3)利用模糊度固定的载波相位观测值进行航空动态定位．试验结果部分主要分析加权电离层模型相比传统模型的优缺点、双差“虚拟”电离层观测值加权精度对模糊度固定效果的影响以及模糊度固定后动态基线定位精度．采用所有数据正确固定所有模糊度作为后续分析参考值,将共180 min数据分割为10 s～20 min的小测段分别进行模糊度固定试验,统计模糊度正确与错误固定百分比．

3.1 三种宽巷模糊度固定方案比较

设计三种方案固定宽巷模糊度:

方案1：

基于MW观测值求解宽巷模糊度,并采用FFV策略控制纳伪概率,固定精度优于0.1周及小数偏差小于0.3周的模糊度;

方案2：

基于“浮点”电离层模型求解宽巷模糊度浮点解,利用3.2节方法选取部分模糊度子集,采用LAMBDA方法固定模糊度,其中ratio检验的阀值为2.0,否则从模糊度子集中剔除“浮点解”的小数部分最大的模糊度重新搜索固定;

方案3：

基于加权电离层模型求解宽巷模糊度浮点解(“虚拟”电离层观测量加权精度为50 cm/100 km),部分模糊固定策略与方案2相同．

为比较三种方案浮点解质量,图6示出了采用观测时间分别为5 min、10 min与20 min的测段进行动态解算得到的模糊度浮点解精度以及偏差．其中,浮点解偏差以正确固定的模糊度为参考值,各方案结果从上至下排列,不同数据长度结果从左至右排列,同时绘出了精度小于0.1周、偏差小于0.3周分布区域,同时在表1中示出了三种方案模糊度正确固定与错误固定百分比．总体而言,累积更多观测数据后各方案模型强度与浮点解质量均得到改善,但方案3模糊度固定效率与可靠性优势等最为明显．

为进一步分析“虚拟”电离层观测值加权精度的给定对整周模糊度固定效率与可靠性的影响,图7示出了不同经验加权精度(σs0/s0分别为20、30、40、50 cm/100 km以及无穷大,即“浮点”电离层模型)、采用不同观测时间长度数据(10～300 s)进行部分模糊度固定试验结果,结果显示本文给定的四种电离层加权精度对宽巷模糊度固定而言区别不大,但“浮点”电离层模型模糊度固定效果与加权电离层模型差距较大．结果分析与理论解释如下:

1)MW观测值受到观测噪声与多路径效应影响,而多路径效应无法通过多个历元平均减弱其影响,且方案1简单地采用FFV策略固定模糊度,其固定效率与可靠性均不如方案2;

2)方案2可累积多历元数据增强模型强度改善浮点解偏差分布,且可利用部分模糊度固定方法提高模糊度固定的效率与可靠性,总体性能优于方案1;

3)方案3浮点解质量以及模糊度固定效果明显优于其他两种方案,累计多历元观测值后(如:观测时间大于10 min)模糊度固定效率与可靠性进一步提升,最终可正确固定全部模糊度．

4)通过调节加权方案,加权电离层模型可灵活地表示长基线、中等基线以及短基线等模型,此处系统地讨论加权精度对模糊度固定效率的影响．首先,不施加约束将影响模糊度固定效率与可靠性:图7中“浮点”电离层模型模糊度正确固定率相对较低且纳伪概率相对较大,较低的正确固定率与模型强度有关,而较高的纳伪概率可由公式(9)解释,当观测数据较少(如:小于2 min),平差后的伪距精度仍然较低,不足以抑制多路径效应的影响．对于施加约束的情况,仅就宽巷模糊度固定而言,给定20～50 cm/km的电离层绝对约束都是合适的,这与宽巷模糊度波长较长可容忍偏差较大有关．

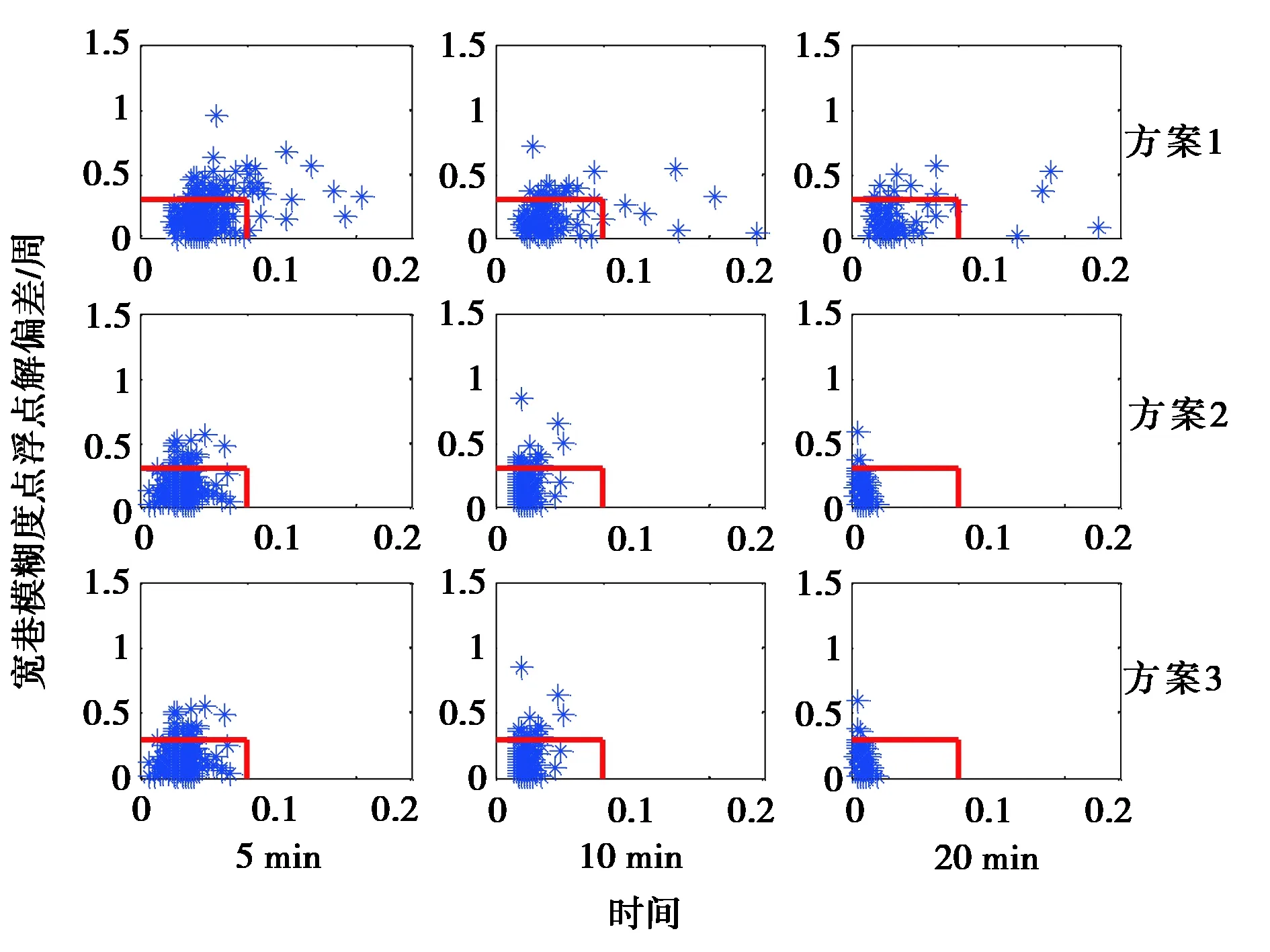
图6 三种模型宽巷模糊度浮点解精度与偏差

图7 加权精度与宽巷模糊度固定效果

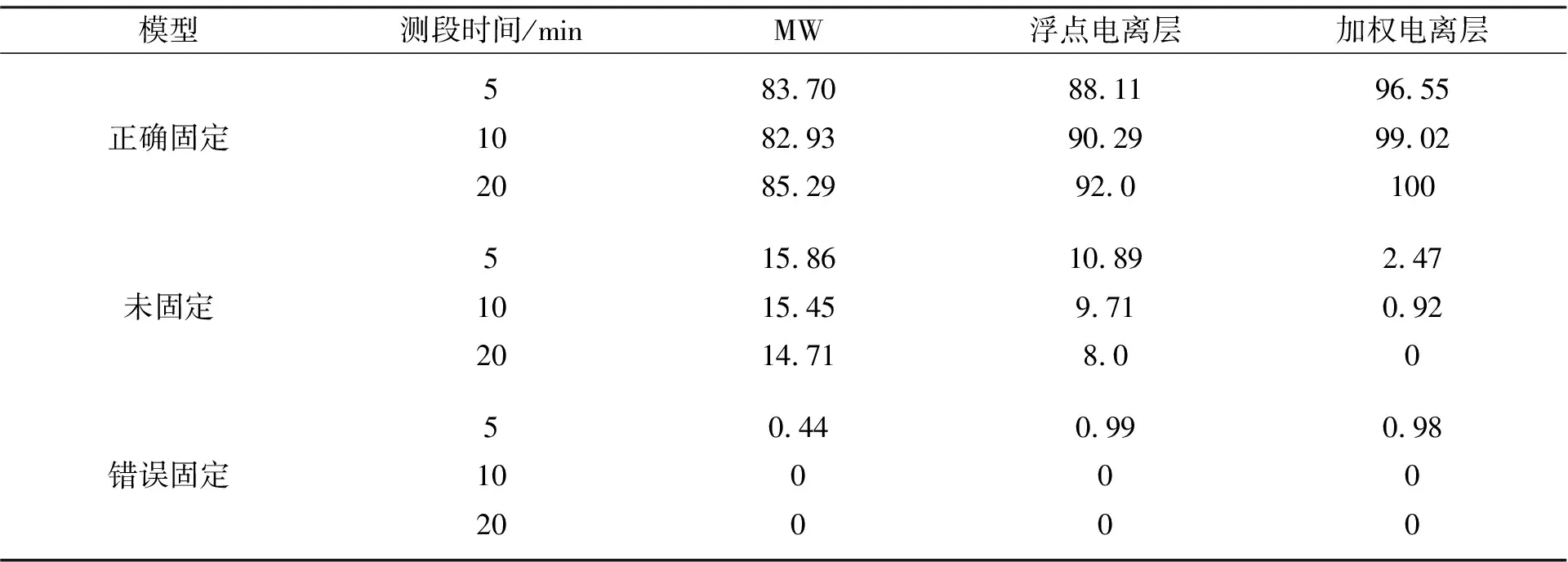
表1 三种方案宽巷模糊度固定效果

3.2 窄巷模糊度固定效果分析

以成功固定的宽巷模糊度为约束得到窄巷模糊度浮点解及其协方差阵,采用2.2节介绍的部分模糊度固定策略,将数据分割为10 s～20 min的测段进行窄巷模糊度固定试验,统计模糊度正确与错误固定百分比．窄巷模糊度固定效果分析包括:①加权电离层模型与“浮点”电离层模型模糊度固定效果对比分析;②给定不同“虚拟”电离层观测量加权精度时模糊度固定效果分析．

为比较加权电离层模型与“浮点”电离层模型窄巷模糊度浮点解质量,图8示出了两种模型窄巷模糊度浮点解精度与偏差结果,结合表2示出的两种模型、不同时间长度数据模糊度固定率,结果表明“浮点”电离层模型的模型强度过低,即使累积较长时间(如20 min)仍然无法固定窄巷模糊度．

与3.1节类似,图9给出了不同观测时间长度数据(10～300 s)进行窄巷模糊度正确固定与错误固定百分比,结果表明“浮点”电离层几何无法正确固定窄巷模糊度,而加权电离层模型窄巷模糊度固定效果与加权精度与观测时间长度有关．对结果的分析与解释总结如下:

1)即使积累多个历元观测数据,“浮点”电离层模型的模型强度仍然过低,浮点解精度低且偏差大:当观测时长为20 min时,窄巷模糊度正确固定百分比仅12%而错误固定百分比高达10%(如表2所示),模糊度固定效率与可靠性均无法满足GNSS动态定位需求．

2)提高“虚拟”电离层观测量权重可提高模糊度固定效率,但过高的权重可能会引入系统性偏差导致纳伪概率增加:图9的结果显示,加权精度为20 cm/100 km时窄巷模糊度正确固定率比加权精度为50 cm/100 km时高出约10%,但纳伪概率约高出1%,这与窄巷模糊度波长较短(约10.7 cm)有关．

图8 两种模型窄巷模糊度浮点解精度与偏差

表2 窄巷模糊度固定率

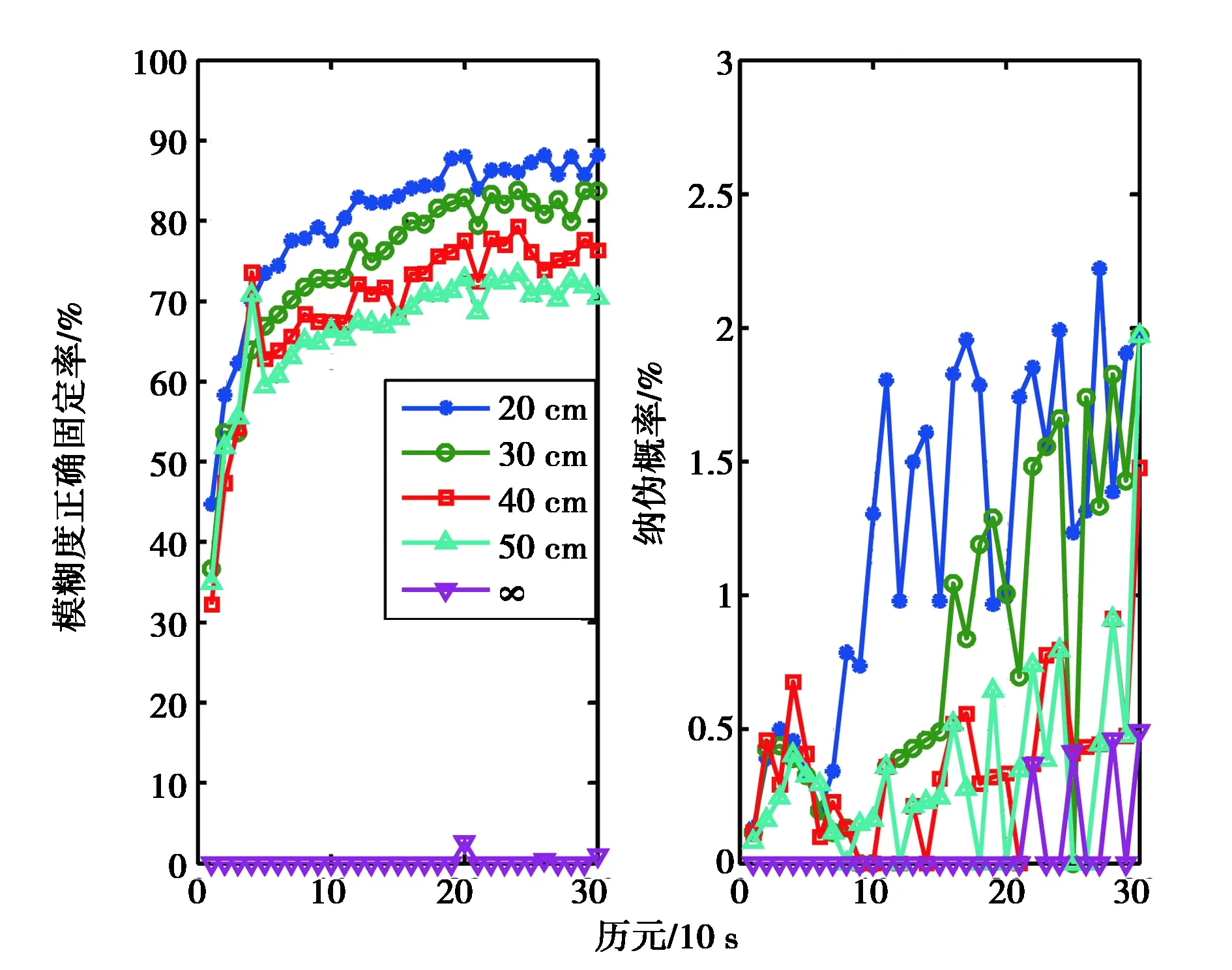
图9 加权精度与窄巷模糊度固定效果的关系

3.3 定位结果分析

为检核航空动态定位精度:1)检核不同卫星观测值残差以评价GNSS定位内符合精度;2)采用商用软件GrafNav动态解算结果检核外符合精度．为便于分析,将双差残差转化为站间单差观测值残差:

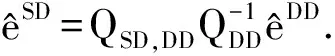
(7)

图10 各卫星无电离层观测值残差 图11 无电离层观测值残差分布

卫星PRN478911171920242832 RMS/cm1.481.491.131.431.390.811.110.931.360.721.46

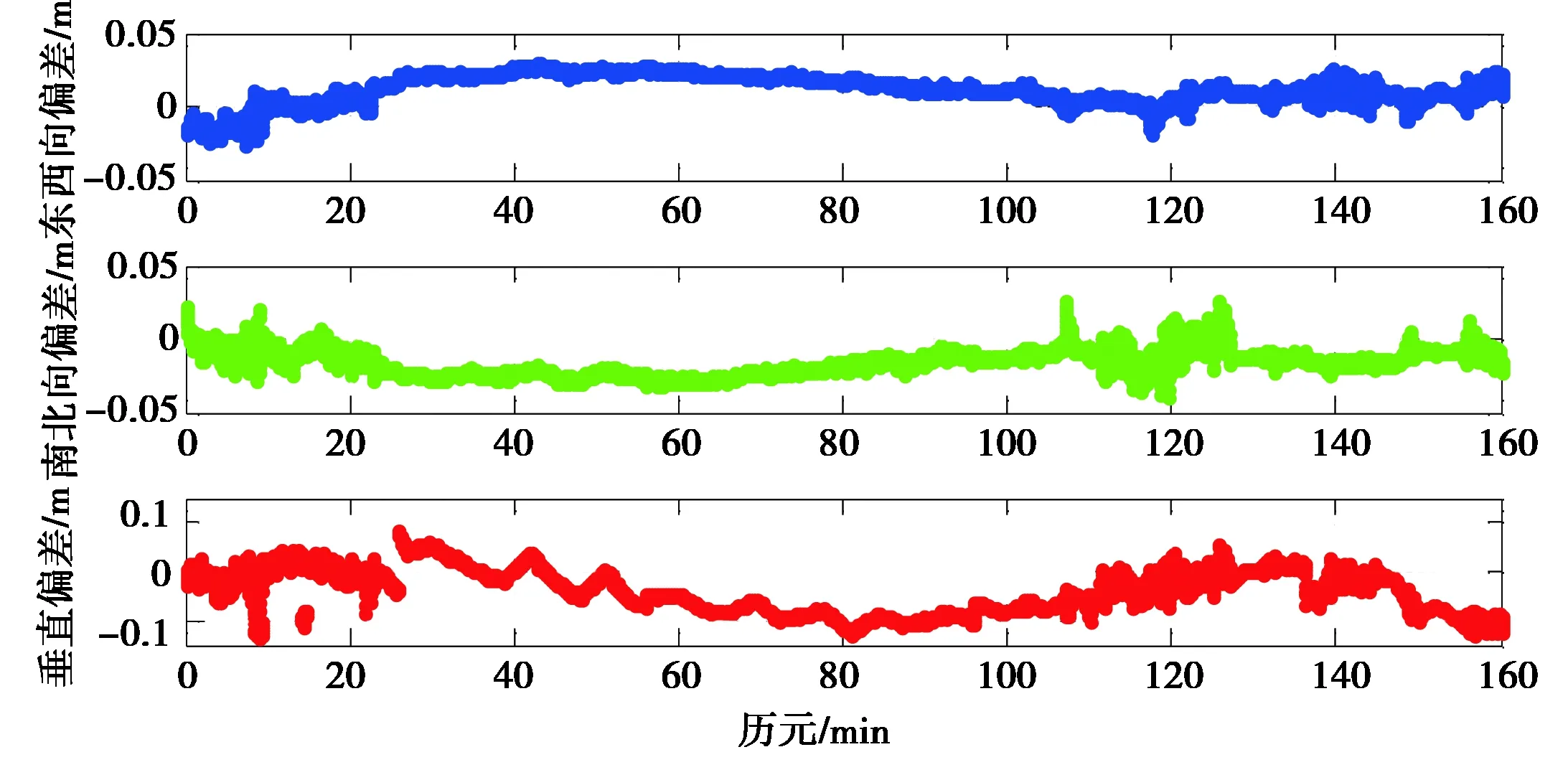
图12 GNSS动态定位结果与GrafNav软件结果之差

4 结束语

从GNSS观测方程出发,分析了无电离层模型、浮点电离层模型与加权电离层模型的特性与各自优缺点．在此基础上,引入动态约束与绝对约束处理双差电离层及对流层延迟误差,加权约束过程中考虑时间/空间尺度变化给予不同权重,实现GNSS短距离与长距离RTK模式有效兼容与过渡．随后,采用宽巷-窄巷序贯固定与部分模糊度搜索固定策略提高GNSS模糊度解算效率与可靠性．最后,基于实测航空动态测量进行GNSS动态定位试验,从模糊度固定效率与可靠性分析、GNSS观测量残差分析、定位精度外符合检验三个方面验证了本文的思想．得出如下结论:

1)基于MW观测值固定宽巷模糊度效率与可靠性较低,其根本原因为MW观测值在消去电离层相关参数、几何相关参数的同时亦损失了参数对应的有效信息;

2)加权电离层模型引入了电离层虚拟观测量,浮点解质量、整周模糊度固定效率以及可靠性相比浮点电离层模型均大幅提高;

3)GNSS观测值残差内符合、定位外符合结果表明,模糊度成功固定后单基线GNSS双频动态事后定位精度为厘米级,可满足于大范围长航时航空动态测量的定位需求．