光刻机掩模台djerk前馈控制算法研究

石婷婷，谈恩民，张志钢，张 霖

（1.桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004；2.上海微电子装备（集团）股份有限公司，上海 201203）

0 引言

光刻机是一种制造大规模集成电路的设备，其发展水平直接决定半导体产品的集成度。近年来，随着半导体技术的迅猛发展，光刻技术及光刻设备的研制成为当今半导体制造行业的焦点[1]。光刻机主要由工件台、掩模台分系统，掩模传输分系统、硅片传输分系统、照明分系统、曝光分系统等几大分系统组成[2]，掩模台的功能是承载掩模版实现高速高加速步进扫描运动。因此，掩模台系统在控制精度、速度、稳定性方面面临着巨大的挑战。开展高速高精度掩模台运动控制算法的研究具有重要意义和工程实践应用价值。

国内外许多专家在光刻机运动台控制算法方面做了大量的研究，现有的控制方法包括前馈控制、鲁棒控制等，均可以获得很好的动态性能[3]，2006年中南大学邓习树博士利用直线电机对掩模台宏动台提出一种不完全微分PID混合扰动观测器的控制方式，系统的跟踪误差在±0.015mm范围内变化[4]。2011年荷兰Hans Butler 采用加速度前馈和反馈复合控制，提高系统的稳定性[5]。2014年哈尔滨工业大学张之万采用了三环PID控制方法分析了磁浮平台摩擦阻力的特性[6]。

目前，在实际的掩模台运动控制系统中，系统的模型会存在一个或多个谐振频率，该频率会随位置变化使伺服性能难以保证，通过阅读文献，位置的四阶轨迹djerk研究较少。因此，本文提出了一种djerk前馈控制方法削弱系统中存在的机械模态对伺服精度的影响。通过仿真与固定的加速度前馈控制对比分析，表明了djerk前馈控制算法有效地补偿固有一阶模态对系统的响应，使整个系统获得了良好的伺服性能。

1 掩模台微动台系统模型设计

为了实现光刻机掩模台超精密运动控制，设计结构时应具有很高的共振频率。一个典型的控制模型可以看做是由刚体模型和一个或多个高频的谐振频率组成。因此，对于单输入单输出系统，掩模台微动台的机械传递函数可以表示为式（1）：

其中，m是掩模台微动台总质量，N为系统共振节点数，wi为共振频率，ξi为对应的阻尼，ki为共振频率处的增益。

2 掩模台微动台伺服控制设计

2.1 复合控制

反馈控制是输出量信息反馈到输入端，通过比较输入值与输出值，产生偏差信号，按照一定的控制规律减小偏差。反馈作用只有在外部作用对被控对象产生影响之后才能做出相应的控制。尤其当被控对象具有较大延迟时间时，反馈控制不能及时调节输出的变化，会影响系统输出的平稳性。这种滞后虽然能满足一般的低精度系统，但是对于实现高速、高加速和高精度的控制系统，即使微小的滞后也会带来很大的偏差信号，影响系统伺服精度。

与反馈控制不同，前馈控制能使系统及时感受到输入信号，使系统提前响应。将前馈控制和反馈控制相结合起来，构成复合控制，使伺服系统跟踪精度大幅度提高。复合控制的前馈设计通常基于加速度、冲击、以及突变，本文前馈控制系统中的前馈系数的设计主要基于加加速度和速度对时间的导数。其控制原理图如图1所示。

图1复合控制原理图中r(s)为输入信号；e(s)为系统误差信号；y(s)为输出信号；P(s)为被控对象传递函数；C(s)为控制器传递函数；F(s)为前馈控制器传递函数；H(s)为反馈通道传递函数。

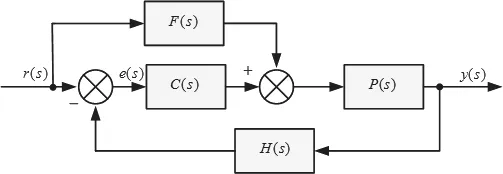
图1 复合控制原理图Fig.1 Composite control schematic diagram

根据复合控制原理图，可以得到复合控制系统的传递函数，如式（2）所示：

当系统为单位负反馈系统时，H(s)=1，可得式（3）：

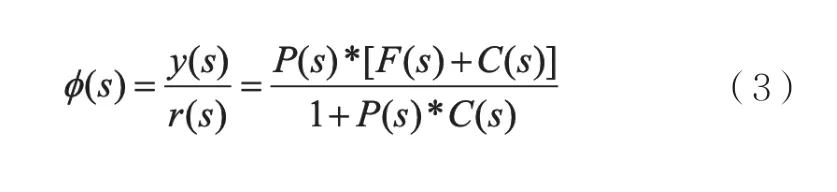
由上式（3）可知，前馈项的引入不会影响系统的特征方程的根，因此并不会影响到系统的稳定性。此外，还能有效提高伺服系统的控制精度。由此，本文引入一种新型加加速度djerk前馈，djerk前馈与加速度前馈联合使用，提高伺服系统的控制精度。

2.2 djerk前馈控制

在运动控制过程中，速度、加速度前馈的使用可以减少运动过程中的伺服误差。然而，在使用了加速度前馈之后，虽然伺服误差被改善，但由于掩模台微动台的模态的引入使系统的控制误差依然较大。对该误差，需要引入djerk进行补偿，该算法实现过程如下。由图1可知，系统误差可以表示如式（4）：

当前馈F(s)恰好为P(s)的倒数的时候，系统误差为零[7]。该值一般都无法直接获得，因此在使用加速度前馈的时候，总有一些与加速度前馈相关的低频噪声存在。对这些噪声需要使用另一种前馈。

在运动过程中，系统的开环误差表示如式（5）：

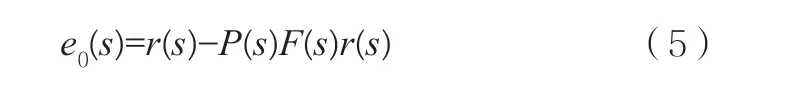
因为F(s)=ms2，所以伺服误差和加速度的关系如式（6）：

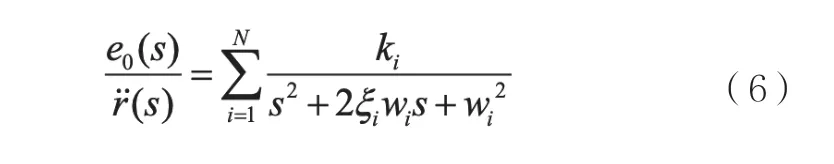
假设系统的本征频率较高，那么上式可以近似表示如式（7）：

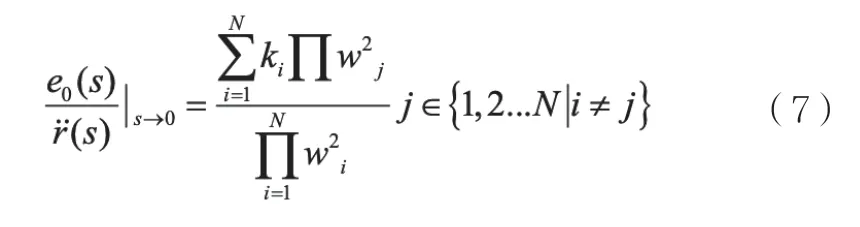
对于新增前馈后的系统，其前馈部分可以写成如式（8）：

其中，r(s)为加速度作用在刚体上产生的位移；Kms2r(s)为加速度作用在模态传函上产生的额外位移；δ/m s2r(s)为djerk作用在刚体上产生的位移，Ks2δs2r(s)为djerk作用在模态传函上产生的位移；K表示共振模态传函。

前馈控制的理想结果是使R(s)=r(s)；从上面的结果来看，加速度前馈产的力作用在模态传函上，使得被控对象有了额外的位移。所以djerk前馈的作用是用来补偿加速度产生的多余的力，有如下关系式式（10）和式（11）：

图2 前馈的控制框图Fig.2 Control block diagram of djerk feedforward

图3 Matlab/Simulink仿真模型Fig.3 Matlab/Simulink simulation model

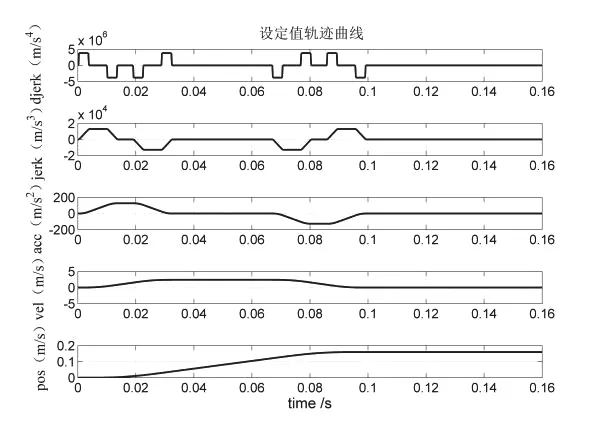
图4 设定值轨迹曲线Fig.4 Set value trajectory curve

3 仿真数据分析

在Simulink中搭建djerk前馈的仿真模型，本文设计的掩模台质量为15.2kg，控制系统的框图如图3所示。

为了验证djerk前馈的控制算法的有效性，本文主要考虑微动台Y方向的运动轨迹。在掩模台的步进扫描运动中，通常采用四阶点对点的运动轨迹进行分析，该设定值轨迹可以防止高速高加速运动轨迹不平滑对台子基础框架的冲击，并且四阶轨迹有效地降低系统跟踪误差。参考轨迹包括加速段、减速段和匀速段。图4是沿Y方向的设定值规划曲线。

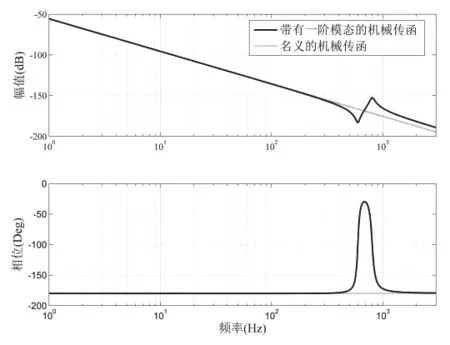
图5 机械传函曲线Fig.5 Mechanical communication curve

图6 开环传函曲线Fig.6 Open loop communication curve

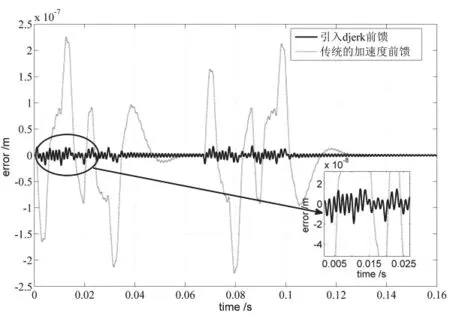
图7 位置误差曲线Fig.7 Bit error curve

图8 PID控制器输出曲线Fig.8 PID Controller output curve

为了进一步验证针对掩模台微动模块控制系统提出的djerk前馈控制方法的可行性和有效性。在模型中人为地设定一个阶的固有频率近800HZ，此固有频率为带宽的4倍，满足实际机台在设计时所考虑的模态。

图5中虚线为刚体模型下的机械传函，实线为带有一阶模态的机械传函。从机械传函上可以进一步验证模型的质量是否符合设计的要求，通过公式12：

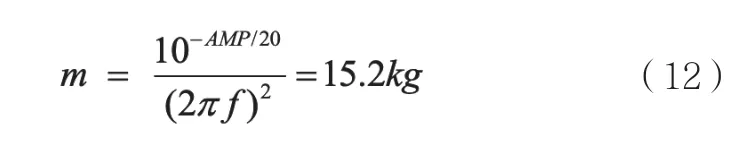
由此验证了模型的正确性。

图6中虚线为名义的开环传函，实线为带有一阶模态的开环传函，从开环传函可以看到带宽为200HZ，相位裕度近似30Deg，幅值裕度近似17dB。满足实际的控制需求。将固定加速度前馈与本文提出的djerk复合前馈的位置误差对比分析。

图7中虚线为传统的加速度前馈的位置误差曲线；实线曲线为引入jerk前馈的位置误差曲线。传统的加速度前馈曲线的位置误差在2.3E～7m，但引入djerk前馈后的位置误差在2E～8m；当施加相同的一阶固有模态时，引入的djerk控制算法对一阶模态的抑制作用比传统的加速度前馈控制明显，说明了djerk前馈控制算法有效地补偿机械模态对伺服性能的影响。

图8中虚线为传统的加速度前馈的PID控制器输出力曲线；实线为引入的jerk前馈的PID控制器输出曲线。在加速度前馈不变的情况下，传统的加速度前馈的PID输出3.5N；djerk前馈的PID输出 0.5N，可以很好地说明加速度前馈+djerk前馈控制器可以很好地改善系统的性能。从曲线上看到红颜色曲线轻微振动，由模型中设定的模态引起的，但其量级比较小。

4 结论

本文针对光刻机掩模台控制系统中存在的机械模态设计一种djerk前馈控制方法，并对此控制方法进行了深入的研究。通过理论的数学推导，在加速度前馈的基础上建立了位置的四阶导数djerk前馈，得出djerk前馈系数。最后利用此控制算法，在matab/simulink仿真验证此控制算法的有效性。从理论分析和仿真结果来看，所提出的控制算法可以在一定程度上削弱系统中存在的机械模态对伺服精度的影响，该算法可以得到比较高的控制精度。传统的加速度前馈的位置误差在2.3E～7m，PID输出近似3.5N；引入djerk前馈后的位置误差在2E～8m，PID输出近似0.5N。综上，djerk前馈有效地减小位置误差，提升了掩模台系统性能。