基于0-1规划模型的大型风电场风机维护方案优化*

王积建

（浙江工贸职业技术学院 人文系，浙江温州325003）

0 引言

据《中国风电发展路线图2050》[1]报告，到2050年，风电将成为我国主力电源之一。虽然近年来我国风电产业得到了突飞猛进的发展，但受主客观因素制约，风电在建设运行中仍然存在一些问题，其中风电运行和管理经验不足是比较突出的问题[2]。

笔者曾以中国华电集团公司甘肃分公司的风电场停机维护问题为题材研制了一个赛题，并有幸被全国大学生数学建模竞赛组委会录用，作为2016年D题使用[3]。

风电场风机维护问题描述如下：已知风电场安装了Ⅰ型风机25台，Ⅱ型风机99台，每种风机的切入风速为3m/s、切出风速为25m/s。针对每一种风机采集了1年365天的2h级风速（m/s）。为安全生产需要，风机每年需进行2次停机维护，两次维护之间的连续工作时间不超过270天，每次维护需一组维修人员（2人为1组）连续工作2天。同时风电场每天需有一组维修人员值班以应对突发情况。风电场现有4组维修人员可从事值班或维护工作，每组人员连续工作时间（值班或维护）不超过6天。试给出每年的风机维护方案，使各组维修人员的工作任务相对均衡，且风电场具有较好的经济效益。

笔者参加了当年国家级获奖论文的评审，发现所有获得全国一等奖的论文，对该问题均没有给出理想的解决方案，即使是荣获全国第一名的论文也不例外[4-6]。究其原因，除了该问题涉及的因素较多之外，还在于学生缺乏针对复杂问题的简化能力和分解能力。如果进一步从日常教学中查找原因，便可发现绝大多数教师在日常教学中都很重视“模型建立”和“模型求解”这两个环节，却忽视了“问题分析”环节，于是就造成了学生在遇到复杂问题时不会简化和分解的弊端。如果在日常教学中重视问题分析环节的训练，使得学生具备化繁为简、化整为零的技巧，那么就可以各个击破而获得完整的解决方案。本文以该题为例，通过对问题的解剖分析，提供一个如何才能化繁为简、化整为零的问题分析思路，供广大建模教师在竞赛培训中参考，并通过建立数学模型给出一个可行的风机维护方案和人员值班方案。

1 问题分析

由于每台风机维护一次需要连续2天才能完成，若将2天折合为1个工期，则全年365天就有182个工期零1天。从全年365天中选择风速最大的一天（这一天不停机维护风机）并删去，剩余364天，然后将1月1日与2日合并为第一个工期，将1月3日与4日合并为第二个工期，以此类推，得到182个工期。

由于每台风机每年维护2次，即上半年和下半年各一次，将1～91工期作为上半年，将92～182工期作为下半年。

如果规定上半年和下半年的维护方案相同，那么问题就简化为只解决91个工期的维护问题，而且全年两次维护之间的连续工作时间是180天，未超过270天，符合要求。

在分析风速时以Ⅰ型风机为例。Ⅰ型风机共采集了365天的风速，每天有12个2h级风速，因此可以将每个工期的24个风速求平均值作为该工期的风速指标，于是全年共有182个风速，再将上半年和下半年对应工期的风速求平均值，就得到91个风速，记作v¯1j，j=1,2,…,91。类似的，Ⅱ型风机的风速 记 作 v¯2j。 在 通 常 情 况 下 ， 有∈ [3 ,25]，∈ [3 ,25]。当风速在[ ]3,25区间时，风速越大，发电功率越大，所以应该选择风速较小的工期停机维护才能使得经济效益最大化，于是问题转化为：将124台风机安排到91个工期、4组人员做维护，如何安排才能使得风电场经济效益最大化，并且工作人员工作量相对均衡？这就是典型的分配问题了，只要建立0-1规划模型就可以解决。

但是，由于目标函数有2个，0-1变量是3维，因此该模型是比较复杂的，而且很有可能模型无解。怎么办？必须想办法继续简化。注意到第一目标是经济效益，即风机由于停机维护而损失的电能，它只与风速有关，而与工作人员的分配无关，于是可以将原问题分解为2个子问题：（1）将124台风机安排到91个工期做维护，如何安排才能使得风电场经济效益最大化？（2）将91个工期的风机安排到4个组做维护，如何安排才能使得工作人员工作量相对均衡？这样一来，每个子问题所涉及的变量变成了二维0-1变量，而且约束条件也少了许多，求解就容易了。

下面开始建模，将子问题（1）称作第一阶段，子问题（2）称作第二阶段。

2 模型建立与求解

2.1 第一阶段

2.1.1模型建立

将n1台Ⅰ型风机与n2台Ⅱ型风机合并在一起，编号为1,2,…,n，n=n1+n2。

设xij=1表示将第i台风机安排到第j工期做停机维护，否则 xij=0，i=1,2,…,n， j=1,2,…,91。v¯1j,v¯2j分别表示Ⅰ型与Ⅱ型风机在第j工期的平均风速。

首 先 分 析 目 标 函 数 。 假 设 v¯1j∈ [3 ,25]，∈ [3 ,25]，则停机维护时平均每台风机的风速为

为了使得经济效益最大化，必须使停机维护造成的电能损失最小化，即

min f （2）

其次，分析约束条件。

（1）每台风机半年内必须维护一次，即

（2）每工期至多安排m-1台风机做维护，即

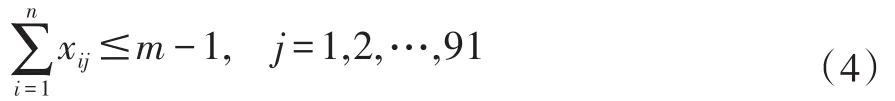
其中，m表示维护人员小组数。

汇总得

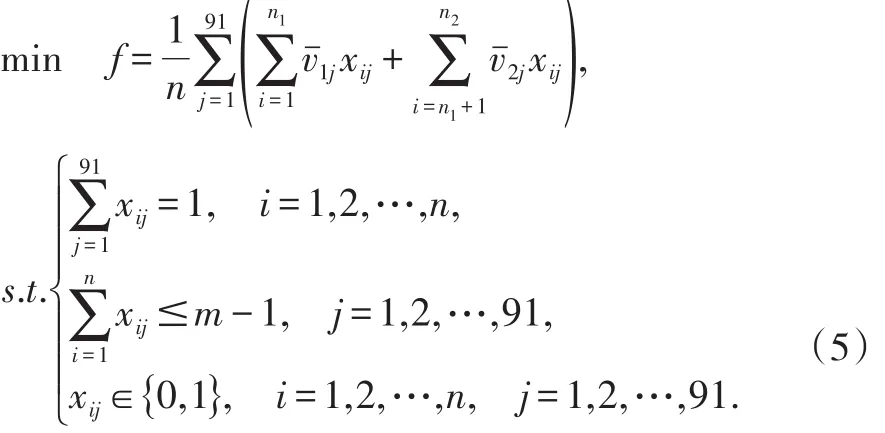
2.1.2模型求解

统计 v¯1j,v¯2j，如表 1 所示。

表1 Ⅰ型与Ⅱ型风机在各工期的风速平均值 （m/s）

从表1可知，Ⅰ型与Ⅱ型风机在各工期的风速平均值都在3～25（m/s）之间，符合建模要求。

使用LINGO软件编程计算[7]，得到最优解f*=4.7，其余结果如表2所示。

表2 各风机被维护的工期（部分）

进一步统计出各工期被维护的风机数量，如表3所示。

表3 各工期被维护风机的数量（部分）

2.1.3结果检验

经过检验，计算结果全部符合约束条件，结果正确。

2.2第二阶段

2.2.1模型建立

假设：（1）所有风机维护难度相同；（2）所有人员技术熟练程度相同。于是在分配风机时可一视同仁。

设yjk=1表示将第k组人员安排到第j工期做停机维护，否则yjk=0，k=1,2,…,m，j=1,2,…,91。

设zjk=1表示将第k组人员安排到第j工期做值班应急，否则zjk=0，k=1,2,…,m，j=1,2,…,91。

首先分析约束条件。

（1）每工期需要维护的风机数量要完成，即

（2）每工期安排一组人员值班，即

（3）每组人员连续上班时间不超过e个工期，即

其中，

e是人员连续工作的工期的阈值。

（4）每组人员值班和维护不能同时进行，即ujk≤ 1, j=1,2,…,91, k=1,2,…,m （10）其次分析目标函数。第一目标是各组维护任务尽可能均衡，即

第二目标是各组值班任务尽可能均衡，即

汇总得

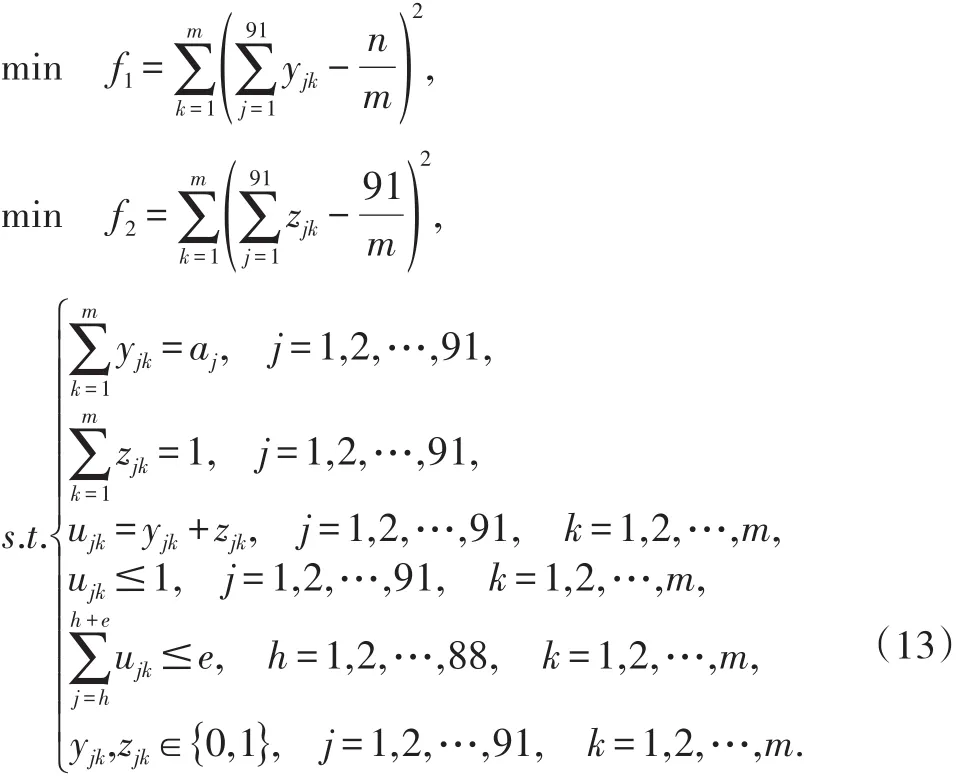
2.2.2模型求解

这是一个双目标规划模型，使用序贯解法[7-8]求解，使用LINGO软件编程计算。

以第一目标求解，先取e=3，无解；再取e=4，得到最优解f*1=0。

将f*1=0作为约束条件，以第二目标求解，程序运行60分钟后终止，得到可行解，f*2=0.74956，其余结果如表4、表5所示。

表4 各工期维护风机的小组（部分）

2.2.3结果检验

经过检验，计算结果全部符合约束条件。

经过统计，各小组维护次数和值班次数如表6所示。

从表6可知，第一目标和第二目标均已经达到，故计算结果是正确的。

3 模型评价

3.1 模型优点

（1）将2个目标的规划问题转化为2个子问题，分2个阶段解决，达到了化繁为简、化难为易的目的。

（2）将风机每年维护2次，本来需要2个维护方案，但规定上半年和下半年的方案相同，就转化为1个维护方案了。

（3）将经济效益用风速指标而不用功率指标来测度，巧妙地避开了拟合风机功率函数这个工作，降低了难度。

3.2 模型缺点

在第二阶段的模型求解过程中，取e=4时才有最优解，意味着某些小组在某些时段其连续工作的天数将超过6天达到8天，超过的2天一般会按照加班来对待。于是，4个小组加班天数可能不够均衡。当然，如果引入第三目标，即加班天数相对均衡，就可以解决这个缺点。

4 结束语

本文以2016年全国大学生数学建模竞赛D题为例，针对优秀论文中暴露出来的问题，诸如面对复杂问题时不会分解、不会简化、不会挖掘信息、不会抓重点等，通过详细的问题分析过程，展示了如何化繁为简、化整为零、各个击破的解题策略，体现了逢山开路、遇水搭桥的建模技巧，也为常规的数学建模教学提供了一个可以借鉴的理想样板。关于这方面的研究，笔者还会继续搜寻素材予以说明。