格上基于身份的云存储完整性检测方案

2019-05-05田苗苗高闯陈洁

通信学报 2019年4期

田苗苗，高闯，陈洁

（1. 安徽大学计算机科学与技术学院，安徽合肥 230601；2. 华东师范大学计算机科学与软件工程学院，上海 200062）

1 引言

云存储是当前应用最广泛的云计算服务之一。用户通过云存储服务将其数据外包给云服务器，之后可以在任何地方通过网络访问其外包数据，从而节省了本地存储开销，提高了使用数据的灵活性。随着越来越多的用户使用云存储服务，云存储安全风险越加凸显[1]，例如硬件故障、软件错误、操作失误、恶意破坏等都可能使云端数据出现损坏或缺失。由于一些商业原因，云存储发生数据损坏后用户通常不能及时获悉，因此用户必须主动检查存储在云服务器中数据的完整性。

由于云端外包数据的规模通常非常庞大，所以下载全部云端数据至本地进行完整性检测的方法是不切实际的。为此，研究人员提出了一些高效的云端数据完整性检测方法，本文统称为云存储完整性检测方案。云存储完整性检测方案通过交互式手段，无需下载全部数据即可验证云端外包数据的完整性。具体地，用户在上传数据时会对数据进行分块处理并计算每块的标签，然后将数据和标签一同上传到云服务器。当验证云端数据的完整性时，验证者将发送一个随机挑战给云服务器，根据块标签的线性同态特性，云服务器能够计算出对应该挑战的一个较短证明。最后，验证者只需验证该证明是否正确，即可判定云端外包数据是否完整。

首个高效的云存储完整性检测方案在 2007年由Ateniese等[2]和Juels等[3]分别提出，其中Ateniese等的方案支持公开验证，即允许任意的第三方验证者检测数据的完整性，并支持无限次的挑战询问；而 Juels等的方案仅支持秘密验证，即只允许数据所有者对数据完整性进行检测，并且仅支持有限次的挑战询问。此后，新的云存储完整性检测方案[4-7]被相继提出，其中大多数方案都支持公开验证和无限次挑战询问。然而这些公开验证方案大都依赖公钥基础设施(PKI, public key infrastructure)，即需要使用数字证书来保证用户公钥和身份的对应关系，所以存在复杂的证书管理问题。

为了消除证书管理问题，一些基于身份的云存储完整性检测方案[8-10]被相继提出。在基于身份的密码方案中，用户的身份即为其公钥，对应的私钥由私钥生成中心(KGC，key generation center)生成[11]。上述方案的安全性都依赖于离散对数等传统数学问题的困难性，而这些数学问题都难以抵抗量子计算机的攻击[12]。由于格上困难问题具有安全性高、量子算法难以破解等优势[13]，使基于格的密码方案受到研究人员的广泛关注。

为了提高云存储完整性检测方案的安全性，近年来一些基于格问题的设计方案相继涌现。2012年，Xu等[14]利用小整数解（SIS, small integer solution）问题[15]设计了首个基于格的云存储完整性检测方案。2014年，Liu等[16]设计了一种格上支持公开验证的云存储完整性检测方案，但没有给出严格的安全性证明。随后，Zhang等[17]指出该方案存在安全漏洞，恶意云服务器可以欺骗验证者通过完整性检测。2017年，Liu等[18]在文献[17]的基础上提出了一种格上基于身份的云存储完整性检测方案，但是由于该方案的块标签涉及云服务器的公钥，云服务器可以利用其私钥伪造数据，所以该方案实际上也不能抵抗恶意云服务器的攻击。

本文提出了一种新的格上基于身份的云存储完整性检测方案，并在随机预言模型下证明了该方案的安全性。与现有同类方案[18]相比，本文方案的系统参数和用户私钥都更短，计算效率也更高。本文的主要贡献如下。

1) 新的标签生成算法。受文献[19]的同态签名算法启发，本文设计了一种新的块标签生成算法。令公钥为和辅助向量文件标识符为τ，则第i块数据zi的标签xi是一个小向量，满足其中是一个安全的散列函数。与文献[19]每次仅处理1 bit数据相比，本算法允许计算较大的数据块，因而能够减少文件的块标签总数，提高标签生成的效率。

2) 高效的私钥提取算法。现有同类方案的私钥提取算法较为复杂，需要较大的计算和存储开销。本文根据文献[20]提出的新陷门算法及相关算法，设计了一种高效的私钥提取算法。对于身份为id的用户Uid，令其中，a是私钥生成中心的公钥，(⋅)是一个安全的散列函数。利用文献[20]中的相关算法，私钥生成中心可以容易地为用户Uid生成较小的Rid作为其私钥，其中Rid满足是一个公开向量。利用函数的高效求逆性和关系用户Uid可以容易地计算任意文件块的标签。

4) 严格的安全性证明。本文方案在随机预言模型下对云服务器的适应性选择身份攻击是安全的，其安全性可以规约到环上的小整数解问题[22-23]（Ring-SIS，ring small integer solution），该问题与理想格上最坏情况下的经典问题一样困难[22]。

2 预备知识

2.1 符号说明

本文的安全参数为n；实数域和整数域分别记为R和Z。向量默认为行向量，用黑体小写字母表示；向量a的转置表示为aT。矩阵用黑体大写字母表示。向量的欧几里得范数为矩阵R的范数其中，riT为R的第i个列向量。矩阵R∈ Rm×w的最大奇异值，记为其中x为 Rw中的单位向量。矩阵R的Gram-Schmidt正交化记为矩阵的行连接记为矩阵的列连接记为[A,B]，即

2.2 格

定义 1 设B∈ Rm×m是由一组线性无关的向量所组成的矩阵，则由其生成的m维格定义为其中B被称为格Λ的基。

对正整数m和q，矩阵定义如下格。

本文基于多项式环结构的理想格[21]。多项式环可表示为其中，为n阶分圆多项式，当n为2的幂时，环R与是同构的，环R中的每个元素都对应于系数向量范数表示为相应系数向量的范数。令整数q≥2，q模环表示为环中多项式的系数本文采用的多项式环为

2.3 离散高斯

离散高斯分布[15,24]是格密码学中的一个重要概念，下面介绍离散高斯的定义和相关性质。

定义2 令参数s＞0，中心c∈ Rm的连续高斯函数

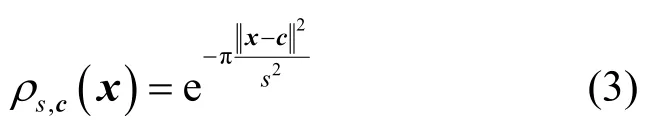
其中，格Λ上的以s为参数，c为中心的离散高斯分布定义为其中，x∈Λ，

当中心c=0时，将连续高斯分布和离散高斯分布分别简写为ρs(x)和DΛ,s(x)。

平滑参数[15]是格中另一个重要概念。以下引理给出了平滑参数大小的一个上界[25]。

引理1 设B∈ Rn×n是格Λ⊂Rn的任意一组基，实数ε＞0，则平滑参数ηε(Λ)满足式(4)。

离散高斯分布有以下基本性质[24]。

引理2 令格Λ⊂Rm，任意实数ε∈ ( 0 ,1)，向量c∈span(Λ)，如果高斯参数s≥ηε(Λ)，那么

从 Rm×k中按照离散高斯分布选择的矩阵，其最大奇异值满足以下条件[21]。

引理3 设实数s＞0，如果矩阵R←DRm×k,s，则以极大概率成立，其中隐含的常数因子约为

文献[21]给出了以下的平滑引理。

引理 4 给定整数n≥4,q≥2和m≥实数和随机向量如果统计接近于Rq上的均匀分布。

2.4 困难问题

本文方案的安全性基于Ring-SIS问题[22-23]，如定义3所示。

2.5 格陷门

格陷门是格密码学的重要工具之一。传统的格陷门是格的一组较短的基[25]。本节回顾文献[20]提出的新格陷门的概念及相关算法。

文献[20]提出了g-陷门的概念，如定义4所示。

文献[20]给出了一种g-陷门生成算法。

根据引理 3可知，陷门R将以极大概率满足

正式地，文献[20]给出了原像采样引理，如引理6所示。

利用上述采样算法可得以下陷门委派算法[20]，如引理7所示。

为简便起见，本文将标签h均设为1。

3 系统描述

3.1 系统模型

如图1所示，基于身份的云存储完整性检测方案由4个实体组成，分别为用户、私钥生成中心、云服务器和审计者。用户是数据所有者，通过云存储服务将其数据外包给云服务器。私钥生成中心根据用户的身份为用户分配私钥。云服务器拥有巨大的存储空间和计算资源，可以为用户提供云存储服务。审计者是一个专业实体，可以代表用户对存储在云服务器中的数据进行完整性检测，并及时将审计结果返回给用户。

图1 基于身份的云存储完整性检测方案模型

不失一般性，本文假定私钥生成中心与用户之间、用户与云服务器之间，以及云服务器与审计者之间均有安全的传输通道。同时，假定每个用户只有一个文件存储在云端。

定义 5 基于身份的云存储完整性检测方案由6个概率多项式时间算法组成，分别为系统建立（setup）算法，私钥提取（extract）算法、标签生成（taggen）算法、审计（audit）算法，证据生成（prove）算法和证据验证（verify）算法。

setup算法：该算法输入为安全参数n，输出为系统公钥mpk和主私钥msk。

extract算法：该算法由私钥生成中心执行。输入系统公钥mpk，主私钥msk和用户的身份id，输出对应的用户私钥skid。

taggen算法：该算法由用户执行。输入为系统公钥mpk，用户的私钥skid和文件Fid，输出为文件的标识符τid，总块数Lid和块标签集合idΦ。最后，用户将上传到云服务器，将发送给审计者，然后删除本地副本。

audit算法：该算法由审计者执行。审计者根据用户身份 id，文件的唯一标识符τid和文件总块数Lid，输出为一个随机挑战chal。

prove算法：该算法由云服务器执行。输入挑战chal，文件Fid及其块标签集合Φid，输出证据P。

verify算法：该算法由审计者执行。输入系统公钥mpk，用户的身份id，审计挑战chal及对应的证据P，输出“0”或“1”。输出“0”表示云服务器中的文件是不完整的，输出“1”则表示文件是完整的。

显然，对于一个正确的基于身份的云存储完整性检测方案来说，如果方案的所有参与方都诚实，那么算法verify应该以极大概率输出“1”。

3.2 安全模型

本文假设私钥生成中心、用户和审计者均是可信的，而云服务器是半可信的，即在数据已损坏的情况下，云服务器可能通过给出有效的证据来极力隐藏数据损坏的事实。根据文献[4]的结论，本文仅需考虑方案的顽健性，它是指云服务器应难以给出一个与诚实证据不同且能通过审计者检查的证据。

本文考虑适应性选择身份攻击下的顽健性，如定义6所述，其中挑战者C模拟私钥生成中心、用户和审计者，而敌手A模拟云服务器。

定义6 如果不存在多项式时间的敌手A能够以不可忽略的概率赢得以下游戏，则称该基于身份的云存储完整性检测方案满足适应性选择身份攻击下的顽健性。游戏由4个阶段组成，分别为建立阶段、询问阶段、审计阶段和伪造阶段。

1) 建立阶段。在该阶段，挑战者 C扮演私钥生成中心的角色。挑战者C执行setup算法生成系统公钥mpk和主私钥msk，并将mpk发送给敌手A。

2) 询问阶段。在该阶段，挑战者 C扮演私钥生成中心和用户的角色。敌手A可以适应性地向挑战者C进行提取询问和标签询问。

① 提取询问。敌手A询问身份id对应的私钥。挑战者C执行算法extract获得私钥skid，并将其发送给敌手A。

② 标签询问。敌手A询问身份为id的用户Uid对文件Fid的标签。挑战者C执行算法taggen生成对应的块标签集合Φid，并将其发送给敌手A。

3) 审计阶段。在该阶段，挑战者 C扮演审计者的角色。对于已经执行过标签询问的文件，挑战者C执行audit算法生成一个随机挑战chal，并发送给敌手A。然后敌手A执行prove算法生成相应的证据P，并将其发送给挑战者C。

4) 伪造阶段。挑战者C提交关于身份id*的挑战询问chal*敌手，敌手A输出一个相应的证据P*。如果P*与诚实的证据不同，A未对id*进行过提取询问且则敌手A 赢得游戏。

4 方案描述

4.1 具体构造

本文提出的格上基于身份的云存储完整性检测方案如下。

1) 系统建立算法

setup：输入安全参数n，选取整数q、p≥2，高斯参数，以及2个安全的散列函数执行下列操作。

① 运行算法GenTrap(1,σ) → (a,R)。

③ 输出系统公钥 m pk=(a,u)和主私钥msk=R。

2) 私钥提取算法

extract：输入系统公钥mpk、主私钥msk和身份 id ∈ {0 ,1}*，执行下列步骤。

① 计算hid=H1(id)。

③ 运行算法 D elTrap(aid,R,s)→Rid。

④ 输出用户私钥 s kid=Rid。

3) 标签生成算法

taggen：输入系统公钥 mpk、用户私钥skid和文件Fid，用户执行下列步骤。

② 将文件Fid分为Lid块，其中每块均属于Rpd，即

③ 计算αi= H2(τid,i)，其中，i= 1 ,2,…,Lid。

④ 计算每块的标签，其中第i块zi的标签

⑤ 输出标签集合Φid={x1,x2,… ,xLid}。

⑥ 将{i d ,τid,Lid}和{i d ,τid,Φid,Fid}分别发送给审计者和云服务器，然后删除本地副本。

4) 审计算法

② 发送 c hal = (i d ,τid,{i,vi}i∈I)给云服务器。

5) 证据生成算法

prove：当收到来自审计者的挑战chal = (i d ,τid,{i,vi}i∈I)后，云服务器找到对应的文件Fid及标签集合Φid，计算然后将证据P= (x,z)返回。

6) 证据验证算法

verify：输入系统公钥mpk，随机挑战chal和证据P，审计者执行下列步骤。

① 解析 c hal=(i d ,τid,{i,vi}i∈I)和P=(x,z)。

④ 计算B= ℓ (p- 1 )2+1。

⑤ 判断下列条件是否均成立。

若是，则返回“1”；否则，返回“0”。

4.2 参数设置

本文的安全参数n设为2的幂次。根据引理1，设函数

根据引理 5，GenTrap算法的高斯参数设为，则系统公钥统计接近于上的均匀分布，主私钥因此根据引理以极大概率成立，其中隐含的常数因子约为

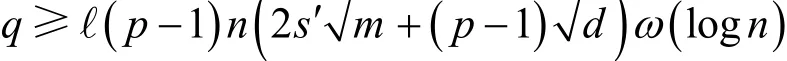
5 方案分析

5.1 正确性

定理 2 如果本文方案中的用户、私钥生成中心、云服务器和审计者都是诚实的，那么verify算法将以极大概率输出“1”。

证明给定用户的身份id和文件Fid，令文件标识符为τid。对第i个数据块zi，计算执行算法根据引理2及引理6，标签xi将以极大概率满足

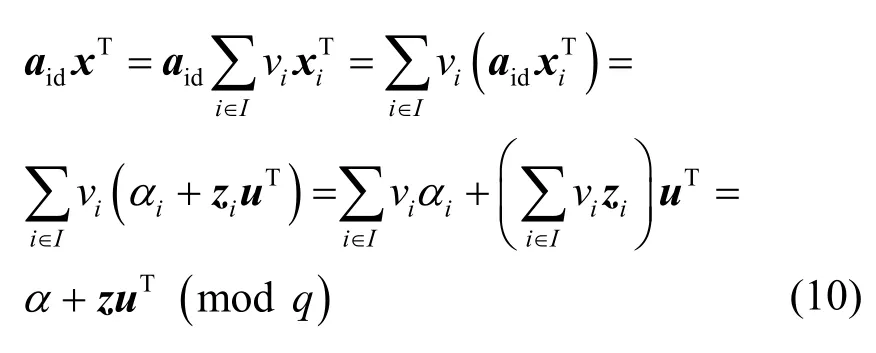
因此，verify算法中的条件b)也成立。

5.2 顽健性

定理3 如果Ring-SIS问题是困难的，那么在随机预言模型下任何多项式时间的敌手都不能以不可忽略的概率破解本文方案的顽健性。

证明根据定义 6，假设存在一个多项式时间的敌手A能够以不可忽略的概率ε破解本文方案的顽健性，则下面证明，存在一个多项式时间的算法B，能以不低于的概率破解Ring-SIS问题，其中，QH是H1询问的最大次数，QE是提取询问的最大次数。具体过程如下。

1) 建立阶段。给定安全参数n，令ℓ≥1为单次审计挑战选择的元素总个数，算法B选择随机整数公开向量高斯参数以及2个作为随机预言机的散列函数输入随机向量作为Ring-SIS实例，令实数则算法B试图寻找一个非零向量使得且算法B最后将系统公钥发送给敌手A。

2）询问阶段。敌手A可以适应性地向算法B进行一系列询问，包括散列询问、提取询问和标签询问。在这个阶段，算法B将建立并维持多个表，其中表L1用于记录H1询问，表L2用于记录H2询问，表Lt用于记录标签询问。

①H1询问。敌手A可以适应性地对身份进行H1询问。不失一般性，假设H1询问在其他类型询问之前且敌手每次提交H1询问的身份都不同。算法C随机选取j∈ { 1 , …,QH}。对敌手A的第i次H1询问，如果i=j，则算法B将(id,b,⊥)存于表L1中，并将b返回给敌手A。如果i≠j，则算法B按照分布选取k个随机的列向量构成计算若hid已在表L1中，则重新选取Rid。最后，算法B将存于表L1中，并将hid返回给敌手 A。根据引理4，hid统计接近于均匀分布。

② 提取询问。敌手A 向算法B适应性地进行提取询问，以获取身份id对应的私钥。此时，算法B检索表L1找到匹配项。若匹配项为(i d ,hid,Rid)，则返回Rid；若匹配项为(id,b,⊥)，则终止。

③ H2询问。算法B建立并维护一个表L2用于响应敌手A的H2询问。一般地，对敌手A的一个H2询问，算法B首先查找表L2，如果找到匹配项则直接将结果返回，否则选择一个随机的α∈Rq并返回。如果A的H2询问形如(τid,i)，则算法B将以一种特殊方式进行响应，具体过程见标签询问。

④ 标签询问。敌手A适应性地进行标签询问，以获得身份为id的用户Uid关于文件Fid的标签。此时，算法B首先查找表Lt，如果找到匹配项(i d ,τid,Φid,Fid)，则直接将其返回给敌手A。否则算法B执行下列步骤：首先选取随机的作为文件Fid的标识符，并将文件Fid拆分为Lid块其中，每块然后计算标签集合其中，xi∈Rm是数据块zi的标签；最后将(i d ,τid,Φid,Fid)存于表Lt中，并将其返回给敌手A。为了计算每个块标签，算法B按照离散高斯分布Dm随机选取xi，计算存于表L2中，并令H2(τid,i) =αi。根据引理4，αi统计接近于均匀分布。

3) 审计阶段。算法B可以对已执行过标签询问的文件进行审计询问。假设算法B希望检测外包文件Fid的完整性。输入文件所有者的身份id，标识符τid，总块数Lid，算法B执行算法 audit( id,τid,Lid)，生成挑战 c hal = (i d ,τid,{i,vi}i∈I)并将其发送给敌手A。敌手A收到挑战后，找到匹配的Fid和Φid，执行算法 p ro v e( chal,Fid,Φid)，生成相应的证据并返回。

4) 伪造阶段。敌手 A 以概率ε输出对应挑战的一个与诚实证据不同的有效证据P∗= (x∗,z∗)。

如果身份 id*不满足H1(id∗)=b，则终止。否则，算法B查询表Lt，找到匹配项假设第i块数据为zi，相应的标签为xi，则由上述构造过程和引理 2可知，且以极大概率成立，其中算法B输出诚实证据P= (x,z)，其中

由于证据P∗= (x∗,z∗)也满足验证条件，即

式(12)与式(11)相减，可得

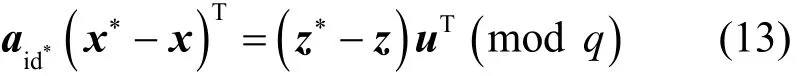
式(13)等价于

由于以上两证据是不同的，所以y≠0。

又由于z和z*均属于 R因此

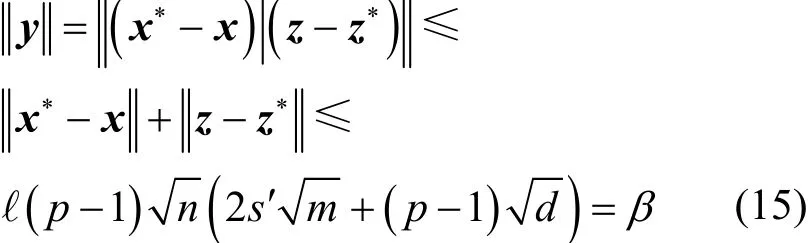
即算法B破解了Ring-SIS问题。

现在计算算法B成功的概率。

算法B成功意味着身份 id*在私钥提取阶段未被询问且H1(id∗)=b。由于身份 id*在私钥提取阶段未被询问的概率不低于而身份 id*满足H1(id*)=b的概率不低于所以算法B成功的概率不低于证毕。

6 性能评估

将本文方案分别与文献[18]和文献[9]中的方案进行实验比较来进行性能评估，其中，文献[18]中的IBRDICL(identity based remote data integrity checking from lattices)方案是基于格的同类方案，而文献[9]中的 IBPDP(identity based provable data possession)方案是基于传统 CDH(computational Diffie-Hellman)假设的方案。这 3种方案的主要特征如表1所示。

表1 3种云存储完整性检测方案的特征比较

性能评估包括方案的存储开销，通信开销和计算开销3个方面。实验代码用C++ 11编写，通过g++ 5.4.0编译。实验由配置了Intel Core i5-4590处理器，8 GB内存和Ubuntu 16.04 LTS操作系统的PC机运行。所有实验结果均是10次实验的平均值。

本文方案的实现使用了 NFLlib函数库[26]，该函数库提供了多项式环上任意操作的快速实现；SampleD算法利用了文献[27]任意模下格Λ⊥(g)的采样算法，该算法将文献[20]任意模下格Λ⊥(g)采样算法的计算开销从O(nl og2q)降低到O(nl ogq)；散列函数使用SHA-256实现，并通过伪随机数生成器生成随机数进行填充。

根据Ateniese等[2]的结论，当文件的块损坏比例为1%时，如果挑战请求包含的元素个数ℓ=460，则审计者能以不低于 99%的概率检测出损坏。因此，本节所有算法均选择ℓ=460。

6.1 对比同类方案

首先将本文方案与 IBRDICL方案进行对比。IBRDICL方案是一种一般格上基于身份的云存储完整性检测方案，该方案所采用的私钥提取算法和原像采样算法效率都较低，实验中将使用与本文方案相同的算法代替；此外，由于本文方案未涉及保护隐私，因此实验移除了 IBRDICL方案中隐私保护所需的计算，主要包括证据生成阶段的一次原像采样运算和证据验证阶段的一次散列运算。

本实验中，2种方案的安全参数n均设为128，其他相关参数如表2所示。特别地，IBRDICL方案中块标签向量的元素个数为nm，单个数据块的元素个数为nd，因此2种方案每个数据块的大小均为2 KB。根据文献[28]可知，2种方案在此参数下具有相近的安全级别。

表2 实验参数设置（n=128时）

1) 存储开销

存储开销主要比较系统公钥长度、用户私钥长度和块标签长度。具体的存储开销比较如表3所示。

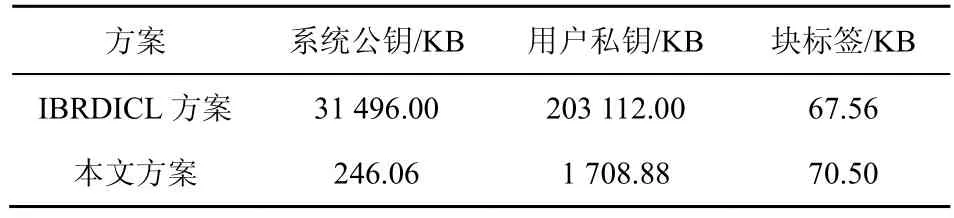
表3 与IBRDICL方案的存储开销比较

由表3可知，IBRDICL方案的系统公钥长度和用户私钥长度都远大于本文方案，而块标签长度比本文方案略小。因此，本文方案的用户存储开销和审计者存储开销都更低，云服务器的存储开销稍高。

2) 通信开销

通信开销主要比较挑战长度和证据长度，具体的通信开销比较如表4所示。

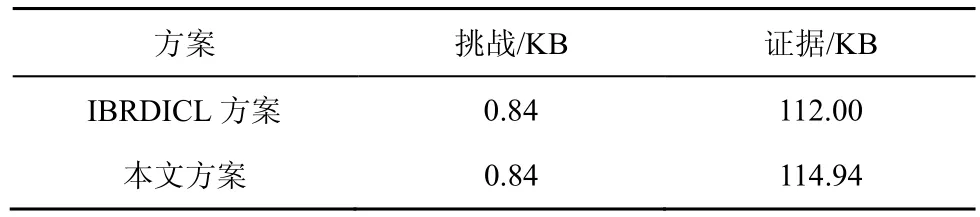
表4 与IBRDICL方案的通信开销比较

由表4可知，本文方案与IBRDICL方案的通信开销相近，仅在证据长度上略大。

3) 计算开销

计算开销包括各算法的运算时间，其中标签生成算法分为离线阶段和在线阶段，离线阶段不依赖于数据，仅计算SampleD算法所需的扰动向量p及apT，因此可以预先执行并将结果保存在本地。标签生成算法的计算开销比较如图2所示，其他算法的具体计算开销如表5所示。

图2中，文件数据块总数的范围是1 000～10 000块，每个数据块的大小为2 KB。由图2可知，2种方案离线阶段所需的计算开销都大于在线阶段的计算开销；相比较而言，本文方案离线阶段的计算开销与 IBRDICL方案比略低；但本文方案在线阶段的计算效率比 IBRDICL方案提高了约93.74%。

表5 与IBRDICL方案的计算开销对比

根据表5，本文方案的系统建立算法和私钥提取算法的计算开销与IBRDICL方案相比都更小。虽然与IBRDICL方案相比，本文方案证据生成算法的计算效率较低，但证据验证算法的计算效率提高了98.81%且总的绝对数值远小于IBRDICL方案。因此，本文方案降低了私钥生成中心、用户和审计者的计算开销。

图2 与IBRDICL方案标签生成算法计算开销对比

综上，相对于 IBRDICL方案中的方案，本文方案降低了用户的存储开销，提高了系统建立、私钥提取、标签生成和证据验证等算法的计算效率，并且数据审计过程的总体计算开销也更低。

6.2 对比传统方案

将本文方案与 IBPDP方案进行对比。IBPDP方案是利用双线映射构造的一种基于身份的云存储完整性检测方案。本实验使用 PBC库（版本为0.5.14）实现IBPDP方案，其中实验参数选自PBC库的参数文件a.param（安全级别约为80 bit），扇区数设为205个（单个数据块长度约为4 KB）。为了达到相近的安全级别和数据块大小，根据文献[28]，本文方案的安全参数n设为512，其他相关参数如表6所示。

表6 实验参数设置（n=512时）

1) 存储开销

存储开销仍然比较系统公钥长度，用户私钥长度和块标签长度。具体的存储开销比较如表7所示。

表7 与IBPDP方案的存储开销比较

由表7可知，IBPDP方案的存储开销与本文方案相比都更小。

2) 通信开销

通信开销也主要比较挑战长度和证据长度。具体的通信开销比较如表8所示。

表8 与IBPDP方案的通信开销比较

由表8可知，本文方案与IBPDP方案相比，仅挑战长度较小，总通信开销仍然较大。

3) 计算开销

本文方案与 IBPDP方案在不同数据块情况下标签生成算法的计算开销如图3所示，其他算法的计算开销比较如表9所示。

表9 与IBPDP方案的计算开销对比

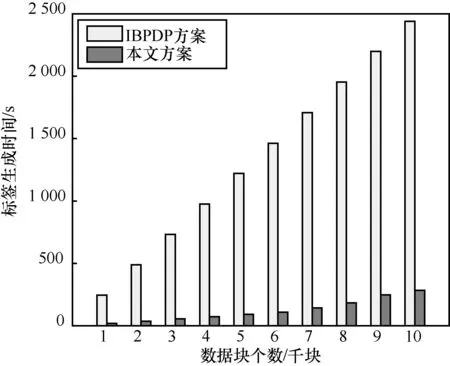
图3 与IBPDP方案的标签生成算法计算开销对比

由于本文方案的标签生成算法分离线和在线两阶段，且离线阶段与数据无关，所以图3仅列出本文方案标签生成算法在线阶段的计算开销，并通过随机替换方法生成扰动向量p。

由图3可知，相比于IBPDP方案中，本文方案标签生成算法在线阶段的计算效率提高了约88.32%。由表9可知，本文方案的系统建立算法和私钥提取算法的计算开销相对较大，但审计算法、证据生成和验证算法的计算效率与 IBPDP方案相比分别提高了99.98%、76.56%和99.73%。由于这些算法执行较为频繁，因此本文方案大大降低了用户、云服务器和审计者的计算开销。

综上，相比于IBPDP方案，本文方案提高了用户、云服务器和审计者的计算效率。