基于门限环签名的可删除区块链

任艳丽，徐丹婷，张新鹏，谷大武

（1. 上海大学通信与信息工程学院，上海 200444；2. 上海交通大学电子信息与电气工程学院，上海 200240）

1 引言

区块链技术[1]运用数据加密、时间戳、分布式共识和经济激励等手段，在节点不需要互相信任的分布式系统中实现去中心化的点对点交易，同时能按照时间顺序将交易相关数据以数据区块的形式存储，其中，数据区块以链条的方式组合成特定数据结构，并以密码学原理保证数据不可篡改和不可伪造，形成去中心化的共享总账。区块链技术以其区别于中心化系统的核心优势，引起了人们的广泛关注，拥有广泛的应用前景[2]。

共识机制是区块链实现去中心化的核心内容，其中基于工作量的证明（PoW, proof of work）[1,3]和基于权益的证明（PoS, proof of stake）[4-5]是最为普遍的区块链共识机制。但是，PoW会造成大量的电力能源损耗，且挖矿过程中产生的算力无法应用于别处，是一种纯粹的算力损耗；而PoS挖矿成本低，容易受到攻击，且挖矿收益与权益的相互促进，使系统日益趋于中心化。2017年，Park等[6]提出了基于空间证明的共识机制（PoSpace, proof of space），通过存储空间的竞争来获得记账权，即竞争节点分别给出自身存储空间大小的证明，验证通过后空间大的节点生成新的区块。同 PoW 和 PoS体制相比，PoSpace基于空间证明，不需要复杂的计算，大大降低了能源消耗，提高了共识效率，且节点的磁盘空间在证明结束后可得到释放，用于下一次竞争，实现了资源的循环使用。

匿名性是区块链交易中实现用户隐私保护的基本要求，而环签名对数据进行认证的同时可确保签名者的匿名性，是区块链研究中的重要工具。环签名是Rivest等[7]在2001年提出的，允许某个成员代表一组用户进行签名，而不泄露签名用户的身份。随后，Bresson等[8]提出了门限环签名，即环中的部分成员只要达到规定的门限值，就可以代表环中所有用户进行签名，该方案提出了公平拆分的思想，并在随机预言模型中可证安全。当签名人数较少时，方案是高效的，但是当签名人数较多时，方案效率较低。Toshiyuki等[9]针对签名人数较多的情况，提出了高效的门限环签名方案，但该方案存在安全问题，详细分析请见本文第3节。Chung等[10]使用双线性对映射，提出了基于身份的门限环签名方案，但效率不高。以上方案都是基于传统的密码学困难问题，如陷门单向函数、离散对数问题等。2011年，Melchor等[11]基于编码理论，提出了高效的门限环签名方案。Zhang等[12]基于 MQ（multivariate quadratic）问题，提出了抗量子攻击的门限环签名方案。

随着区块链的发展，存储所有区块数据需要巨大的存储空间，对于普通节点来说存储代价很大。而在实际应用中，有的区块数据已经过期或失效，比如已经宣布破产的银行交易信息、已经废除的法律文件等。这些数据永久存储在区块链中已经失去了价值，且占用大量空间，造成资源浪费。如果经大多数用户同意后，可删除这些失效的数据，而又不影响区块链中其他数据的存储和使用，有助于释放节点的存储空间，降低存储代价，具有重要的应用价值。目前绝大多数区块链结构是不允许删除数据的，数据一旦写入链中就不能更改，可能会造成过期数据占用大量存储空间的问题。

在区块链研究中，爱哲森公司基于变色龙散列，提出了可编辑区块链技术[13]。只要知道变色龙散列的陷门，就可以找到已有数据的一个碰撞，从而实现对区块链数据的编辑。但在该方法中，散列函数的陷门存储在一个可信中心，因此对数据的编辑权过于中心化。Li等[14]使用秘密共享技术，将变色龙散列的陷门分成多份，并分配给各个网络节点。当一半以上的网络节点同意时，可恢复散列函数的陷门，找到已有数据的碰撞，对区块链数据进行修改。以上2种方法均使用变色龙散列，而目前的区块链结构大多使用抗碰撞的散列函数，因此上述方法的适用范围非常有限。基于抗碰撞的散列函数，本文提出了可删除的区块链方案，适用于大多数区块链结构，具有广阔的应用前景。

本文首先分析了文献[9]中的门限环签名方案，指出了该方案的安全问题，提出了改进方案，并在随机预言模型中可证安全。随后，使用改进的门限环签名方案，基于空间证明的共识机制提出了可删除的区块链。当数据过期或失效时，经大多数用户同意并签名，对过期数据进行删除，并保持区块链的结构不变，不影响其他区块的存储和使用。所有人可对数据进行验证，包括被删除数据的相关信息。

2 基础知识

2.1 门限环签名

环签名[7]主要包括以下算法。

setup算法：输入安全参数λ，输出n个环成员的公钥PK1,…, P Kn和私钥SK1,…,S Kn。

ring-sign算法：输入消息m、n个环成员公钥PK1,…, P Kn和签名用户私钥SKS，输出环签名σ。

ring-verify算法：输入环成员公钥PK1,…,PKn和签名(m,σ)，输出“接收”或者“拒绝”。

安全的环签名需要满足正确性、不可伪造性以及匿名性，即合法环签名可以验证通过，非环成员不能伪造合法的环签名，且任何人不能获得环签名用户的真实身份。

在此基础上，门限环签名[8]包括以下算法。

setup算法：输入安全参数λ，输出n个环成员的公钥PK1,…, P Kn和私钥SK1,…,S Kn。

T-ring-sign算法：输入消息m、n个环成员公钥PK1,…, P Kn和n-t个签名用户私钥SKi,1,… ,SKi,n-t，输出环签名σ。

T-ring-verify算法：输入环成员公钥PK1,…,PKn和签名(m,σ)，输出“接收”或者“拒绝”。

本文所提环签名方案中用到了文献[7]中提出的用户拆分方法，下面做简要介绍。

定义 1 公平拆分[7]。假设系统中n个用户被拆分为t个子集π=(π1,… ,πt)，I= {i1, …,it}表示其中t个用户编号的集合。对于集合I，如果对于所有的j∈[1,t]，均有就称π是一个公平拆分，其中#(X)表示集合X中元素的个数。

如文献[7]所述，为了确保环签名中用户的匿名性，对于任意包含t个用户的集合，都要存在一个公平拆分，称为完备拆分系统。具体定义如下。

定义 2 完备拆分系统[7]。令t＜n-t＜n，对于任意包含t个用户编号的集合I，都存在一个公平拆分，这样的系统称为(n,t)-完备拆分系统。

2.2 环签名安全模型

本节介绍门限环签名方案的安全模型，即选择消息攻击下的强不可伪造性（SU-TRS-CMA, strong unforgeability against chosen message attack in a threshold ring signature scheme）。

定义3 SU-TRS-CMA。假设环中共有n个成员，其中n-t个成员可代表所有用户签名。通过以下游戏，本文定义TRS（threshold ring signature）方案在选择消息攻击下的强不可伪造性[8,15]。游戏包含2个参与者：挑战者和敌手。具体包括以下步骤。

setup 挑战者执行setup算法获得所有环成员公钥PK1,…, P Kn和私钥SK1,…,S Kn，并发送公钥给敌手。

阶段1 敌手适应性地进行下列询问。

散列询问：敌手发送字符串给挑战者，挑战者选择随机数作为对应的散列值，并返还给敌手。

私钥询问：敌手发送用户公钥给挑战者，挑战者返回对应私钥给敌手，敌手至多可询问n-t-1个用户的私钥。

签名询问：敌手发送消息m给挑战者。挑战者随机选择n-t个环成员私钥根据T-ring-sign算法生成签名σ，并返回给敌手。

挑战阶段 假设敌手能以不可忽略的概率ε伪造有效的门限环签名，并将消息m*的环签名σ*发送给挑战者，且 (m*,σ*)没有出现在签名询问阶段。挑战者可根据 (m*,σ*)，以不可忽略的概率ε′解决单向函数的求逆问题。

在上述游戏中，敌手的优势定义为ε，即成功伪造门限环签名的概率。如果对于任意t多项式时间的敌手，在经过q次询问后，至多能以概率ε伪造有效的环签名，则称门限环签名方案在选择消息攻击下是(t,q,ε)-强不可伪造的。

由以上安全模型，如果门限环签名方案满足强不可伪造性，则攻击者即使得到消息m的签名σ，也不能伪造m的其他有效签名

2.3 基于空间证明的区块链

PoSpace共识机制[6]基于“一定时间内需要一定空间构造一个结构图”这一事实，展开空间竞争。首先，介绍空间证明过程。如图1所示，设定有向无环结构图为顶点集合，N为顶点个数，E为有向边集合。图中各顶点因为有向边而存在一定的联系，为进一步表示顶点之间的联系，突出该图的结构，为每个顶点设置与之相关联的标签值，具体为

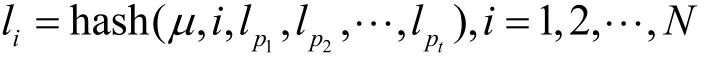
其中，i为顶点序号，μ为可设定的随机数，为链向当前顶点i的所有前向顶点，即其母顶点的标签值。这样，每个顶点与其母顶点便依靠标签值联系起来，形成了基于顶点标签值的有向图结构。

图1 有向无环结构图

从图1可以看出，要实现对以上结构图的存储需要一定的空间，空间越大，越容易实现结构图的存储与恢复。而在空间不足时，只能多次利用仅有的空间存储相关数据，反复存储与删除，以时间换取空间。因此当时间一定时，空间大小不同的矿工对同一结构图的存储效率便高低不齐，产生基于空间的竞争。PoSpace正是在这样的模型下建立的。

PoSpace共识系统会生成如图1所示的结构图，每个矿工都可以依据自己的空间大小，最大程度并最优化地存储该结构图。系统会选择存储空间最大的矿工作为最终的记账者。因此，基于空间证明的挖矿过程就是矿工证明自己拥有足够大的空间，以便高效存储结构图的过程。矿工拥有的空间越大，挖矿成功的概率也越大。挖矿的具体实现过程可参考文献[6]。

接下来，介绍基于空间证明的区块链结构，如图2所示。

由图2可知，每个区块i都分为3个子块：证明子块iφ（hashiφ）、签名子块iσ（signatureiσ）和交易子块iτ（transactioniτ）。其中，证明子块又称散列子块，是对相关内容做散列运算后的结果。

1) 散列子块iφ包含：当前区块序号i，记账者对前一区块的散列子块φi-1的签名φζ，记账者在竞争记账权时给出的承诺证明以及空间证明

2) 签名子块iσ包含：当前区块序号i，记账者对当前区块的交易子块iτ的签名τζ，记账者对前一区块的签名子块σi-1的签名

3) 交易子块iτ包含：当前区块序号i，交易信息列表ctx。即

3 改进的门限环签名方案

3.1 IT-TRS方案及安全性分析

首先，回顾一下 IT-TRS（TOSHIYUKI I,KEISUKE T- threshold ring signature）方案[9]。

假设系统中有n个用户，其中n-t个用户可代表所有用户生成环签名，其余t个用户不参与签名。令表示非签名用户，而表示非签名用户编号的集合。假设通过拆分，所有用户被拆分为t+1个互不相交的子群，则至少有一个子群中的用户都参与了签名，称这个子群为合法子群。如文献[8]所述，为了确保环签名的不可伪造，需要采用(n,t+1)-完备拆分系统。

setup算法：令l表示安全参数，完备拆分系统，其中，表示一次公平拆分，记表示一组用户编号的集合。令表示所有n个用户。对于每一个i=1,2,…,n，gi表示匿名的单向陷门映射。对于任意i和j，j中元素的个数，Q表示的最大值。令如果对于所有的都是签名者，称是合法的。如文献[8]所述，对于所有的整数n和t，且t≤n，(n,t+1)-完备拆分系统一定是存在的，每个用户Pi基于单向陷门映射gi进行签名。

对于每个子群πij，定义单向陷门映射为

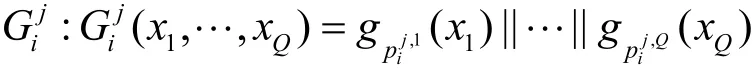
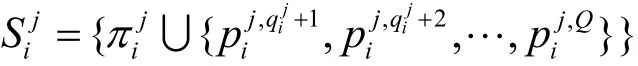
T-ring-sign算法：假设系统中至多有t个用户不参与签名。由于所有用户被分为t+1个互不相交的子群，则每次拆分都存在一个合法子群，记为设签名消息为m，H为输出长度为Qlbit的hash函数。对每个，签名者执行以下步骤。

步骤 2 对于k=j+1,…,t+1,1,2,…,j-1，随机选择其中

图2 基于空间证明的区块链结构

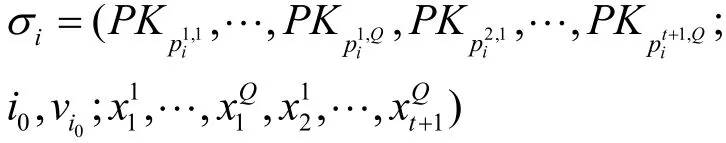
因此，消息m的最终签名

T-ring-verify算法：对于签名iσ，验证者计算

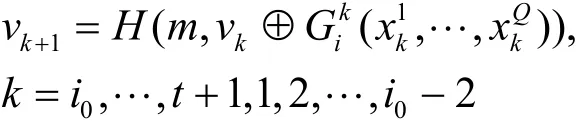
通过分析，上述方案中的门限环签名不满足强不可伪造性。假设合法子群 πij按照上述算法生成消

息m的签名σ，则非合法子群 πij+1可与合法子群中的某个用户相勾结，生成消息m的另外一个合法签名。不妨设非合法子群与合法子群中的用户相勾结，攻击过程如下。

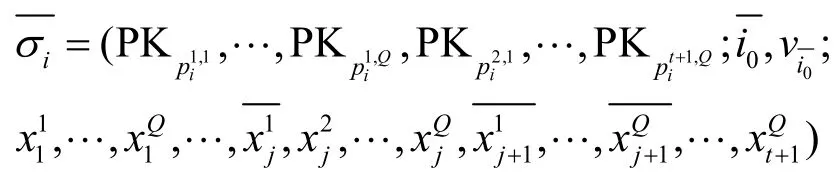
把以上过程重复p次，生成最终的签名

由验证算法可知，上述签名可以通过验证。攻击成功的原因在于随机数的改变只影响的值，而对没有影响，因此攻击者只要知道的某个陷门，就可以伪造签名通过验证。

3.2 改进的TRS方案

针对上述攻击方法，本文提出了改进的 TRS（I-TRS, improved threshold ring signature）方案，满足门限环签名的强不可伪造性及用户的匿名性。

假设系统中有n个用户，其中n-t个用户可代表所有用户生成环签名，其余t个用户不参与签名。改进方案中的数学符号与原方案相同。

setup算法：同原方案。

T-ring-sign算法：假设系统中至多有t个用户不参与签名。由于所有用户被分为t+1个互不相交的子群，则每次拆分都存在一个合法子群，记为设签名消息为m，H为输出长度为Qlbit的 hash函数。对每个 πi,i= 1 ,2,… ,p，签名者执行以下步骤。

步骤 2 对于k=j+1,…,t+1,1,2,…,j-1，随机选择

因此，消息m的最终签名

T-ring-verify算法：对于签名iσ，验证者计算

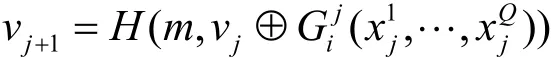
改进方案解决了原方案存在的问题，是一个安全的环签名方案。

3.3 改进TRS方案安全性分析

本节对改进TRS方案进行分析，包括签名的强不可伪造性及签名者的匿名性。

1) 强不可伪造性

在随机预言模型中，假设敌手最多可勾结(n-t-1)个非签名者，在经过qH次散列询问后，能以概率ε伪造(n-t,n)门限环签名，则对于陷门单向映射知某个输出y0，可构造算法以概率找到输入x0，使

证明 本文需要在选择消息攻击下证明门限环签名的强不可伪造性（SU-TRS-CMA）。游戏包括2个参与者：挑战者和敌手。假设敌手在经过询问后可伪造有效的门限环签名，则挑战者已知陷门单向映射的输出y0，可构造算法找到对应输入具体步骤如下。

setup 挑战者为所有用户生成公私钥对，并将所有用户公钥PK1,… ,PKn发送给敌手。

阶段1 敌手适应性地进行下列询问。

散列询问：敌手发送字符串给挑战者，挑战者随机选择Qlbit的随机数v，并设定某2个字符串的散列值分别为v和v⊕y0，其余字符串选择Qlbit的随机数作为散列值，并返还给敌手。

私钥询问：敌手发送用户公钥给挑战者，挑战者返回对应私钥给敌手。敌手至多可询问(n-t-1)个用户的私钥。

签名询问：敌手发送消息m给挑战者。挑战者随机选择(n-t)个环成员私钥根据T-ring-sign算法生成签名σ，并返回给敌手。

挑战阶段 假设敌手能以概率ε伪造消息m*的环签名且没有出现在签名询问阶段。

2) 匿名性

3) 效率分析

假设系统中有n个用户，其中n-t个用户可代表所有用户生成环签名。当t很小，即签名人数很多时，所提改进方案是效率最高的，如表 1所示。为了公平起见，本文只比较传统的门限环签名方案。

表1 不同方案的门限环签名效率比较

4 可删除的区块链

本节基于改进的门限环签名方案，提出可删除的区块链结构，并做仿真实验进行模拟实现。当区块链数据过期时，只有绝大多数用户同意，并生成有效的门限环签名才能进行删除，否则不能进行删除。除删除操作外，不能对区块数据做其他更改。在删除区块数据时，不能影响其他区块数据的使用和验证。

4.1 数据删除概述

假设某个区块i+1的交易数据因为数据过期、废弃等原因，不再具有链上存储以供溯源的意义。继续存储该区块的交易数据无疑是对存储资源的浪费。在此情况下，网络中的相关节点向网络广播“删除区块i+1交易数据”的请求信息，具体表示为：DelTx={number, reason}，其中，number=i+1为请求删除的交易数据所在的区块号，reason即为请求删除的原因。其余所有合法节点在接收到DelTx后，会对该删除操作的合理性进行考证，比如该区块交易数据是否真的来自一个已经宣布倒闭的银行等等。考证过后，合法节点需广播自己关于DelTx的意见，记为 ReDelTx。ReDelTx=1，表示节点同意删除请求；ReDelTx=0，表示不同意删除请求。最终，每个节点均可统计整个网络对该删除信息的反馈，如果“同意”信息超过设定门限（本文设为全网节点的 75%），便认为该删除请求合法，然后生成一条专属的删除消息m，其具体格式将在第 4.2节中介绍。

接下来，对该删除消息持“同意”意见的节点将进行交易数据的删除工作，并成为环签名系统中的签名节点，按照第3节中提出的改进门限环签名方案，代表整个系统生成消息m的门限环签名，作为对删除消息m合法性的承诺。同时还将生成的环签名存储于交易数据原本所在的位置，并在全网进行广播，以供所有节点对该删除操作的合法性进行验证。

所提方案是在公链模式下，基于PoSpace共识机制提出的区块链数据删除方案。在目前使用PoSpace共识机制的区块链中，链上交易数据都是公开的，可供全网节点公开验证，不能实现交易数据的隐私性。因此，方案面向的区块数据都是公开可验证的，删除交易数据时对数据进行公开考证是合理的，删除操作不会增加数据的隐私泄露风险。如果用户对隐私性要求较高，可将数据存储在能实现隐私保护的区块链中，如 Zerocash[16]、Monero[17]等。

4.2 区块链结构

假设第i+1个区块数据可以删除，经大多数用户同意并生成门限环签名，对数据进行删除。可删除的区块链结构如图3所示。

在第i+1个区块中，包含3个子块：证明子块签名子块和门限环签名子块证明子块和签名子块如第2.3节所述，这里只介绍门限环签名子块

区块数据删除后，由签名节点广播至全网。其余用户首先验证门限环签名是否正确，然后将中对被删除交易子块τi+1的签名τζ与签名子块σi+1的签名τζ进行比较，若一致则接受删除行为，否则不接受。

图3 可删除的区块链结构

对比交易数据删除前后的区块信息可知，除交易数据被替换成相应环签名外，当前区块及其前后区块中的其余信息都未发生任何变化，区块链的结构未发生变动。可见，所提区块链方案可以成功删除区块中废弃的交易数据，释放大量存储空间，且不影响其他区块数据的使用和验证。

4.3 数据删除安全性分析

本文通过阈值设定，在全网75%节点同意时，才可生成删除消息m，并由同意删除的节点生成m的门限环签名，承诺数据删除的合法性。门限环签名本身具有的正确性、匿名性和强不可伪造性保证了该承诺的安全有效，并可供任意节点随时进行验证。其中，阈值比例75%的设定是综合考虑“门限环签名效率”“节省存储空间”“删除操作是否代表大多数节点的意见”这3点，并通过实验测试得出的。一方面，阈值越高，越能代表系统中更多节点的意见，让删除操作更加安全。但另一方面，阈值过高将导致删除区块耗时太长，影响删除操作的效率，降低数据删除的应用价值。因此权衡两者，将阈值比例设定为75%，可在保障安全性的前提下也保证方案效率。

同时，由第4.2节的分析可知，整个交易数据的删除过程并不会破环原有区块链的结构。区块数据删除后，门限环签名被存储于原有数据所在位置。当前区块的证明子块和签名子块信息并未发生改变，因此该区块仍然与前后区块保持合法的链接关系。交易数据删除后，区块中签名子块关于交易数据的签名与门限环签名中包含的交易数据签名是一致的，其他网络节点将通过验证该一致性以确定区块链接的合法性。

综上，可删除的区块链具有以下特点。

1) 只有大多数用户同意才能对数据进行删除，避免恶意删除。由门限环签名的强不可伪造性可知，当区块数据过期或失效时，只有超过门限个数的用户才能生成有效的环签名，否则不能生成签名并通过验证。因此，本文可以设定合适的门限值，确保绝大多数用户同意才能删除区块数据，避免恶意用户的删除。

2) 除删除操作外，不能对区块数据做其他更改，例如插入数据、删除部分数据等。在基于空间证明的区块链中，每个区块中都包括证明子块和签名子块，证明子块可以认证记账者的身份，签名子块是记账者对交易数据的认证。如果恶意用户更改区块数据，例如插入数据、删除部分数据等，则需要重新生成签名子块，但是记账者的签名是不能伪造的，因此数据不会更改成功。

3) 第i+1个区块数据的删除并不影响其余区块的链接。原因如下：交易数据的删除只是把原有区块中的交易子块τi+1变成了门限环签名子块并不改变证明子块φi+1和签名子块σi+1，因此它们与前后区块的链接关系不受影响。

4.4 实验仿真

本节分别对区块的生成和删除进行了仿真实现。挖矿节点使用的实验设备配置为2.4 GHz Intel i5 处理器，4 GB内存，并在Visual Studio Ultimate开发环境下，使用C++语言编程实现。在生成区块链时，散列函数和记账节点签名分别使用 SHA（secure hash algorithm）-256和DSA（digital signature algorithm）-512实现。在删除区块链时，使用第3节提出的门限环签名，其中的单向陷门函数使用RSA-1024实现。

4.4.1 基于空间证明的记账权竞争

如第2.3节所述，在PoSpace共识机制下，矿工们基于空间证明对记账权展开竞争，首先模拟空间竞争过程。

假设系统生成如图4所示的有向图，共包含20个顶点。

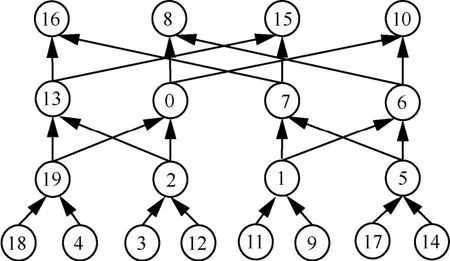
图4 系统有向图

设有5位矿工，分别记为A、B、C、D、E，每位矿工都可根据自己的公钥，计算该有向图中每个顶点的标签值（使用SHA-256实现），生成结构固定但顶点标签值与身份一一对应的专属有向图。由于空间限制，部分矿工无法一次性存储全部顶点，只能完成对部分顶点的存储，其他非存储顶点则需要依据有向图结构和已存储的顶点计算得到。当系统随机要求矿工返回相关顶点标签值时，本地空间大、存储顶点多的矿工总是拥有较大的优势，以最快的速度响应系统，从而赢得记账权，这样便形成了基于空间的记账权竞争。其中，5位矿工的公钥及其对图4有向图的存储情况如下。

每个矿工都作为一个空间证明者P向系统扮演的验证者V证明自己拥有足够的空间存储全图，V多次发布验证顶点标号集合，记为向P发起挑战，要求P返回Ch中每个标号对应的顶点标签值及其母顶点标签值，以验证P是否有足够大的空间存储全图，P返回相应数值响应V发起的挑战。表2记录了上述5位矿工在不同挑战Ch下的空间证明时间。

表2 5名矿工空间证明时间比较

由表2可知，在不同的挑战Ch下，P的空间越大，对V的挑战的响应就越快，越容易获得记账权，这便是基于空间证明的PoSpace共识机制下区块记账权竞争的基本过程。

4.4.2 新区块的生成

当节点获得记账权后，依次生成新区块的证明子块（hash子块）、签名子块和交易子块。原始区块33～35的数据如图5所示，本文以区块35为例进行说明。

图5 原始区块33～35的数据

4.4.3 区块的删除

假设当前区块链中，编号33～35的区块信息如图5所示。其中，区块34中的交易数据已过期，为了节约存储空间，区块链中的各个节点于 2018年7月3日达成共识，对该区块执行删除操作。首先，由区块 34删除时间“20180703”、删除原因“overdue”和记账者对区块 34中交易数据的签名“57B55F59A500212FDEBC6F92BC8B14F46444BF DE”，生成删除行为对应的消息m= “3420180703 overdue57B55F59A500212FDEBC6F92BC8B14F46 444BFDE”，并按照第3.2节中的改进算法，对消息m生成门限环签名，记录在原始交易子块中。

假设系统中总用户数n=8，环签名门限值为6，则非签名用户数t=2。设签名用户集合记为非签名用户集合记为设某次拆分方法为：

将上述过程重复p次，得到最终的门限环签名其中，

当区块 34中的交易数据删除后，区块 33～35的数据如图7所示。

删除操作完成并广播后，网络中所有节点均能对门限环签名进行验证，并将消息m中记账者对区块 34中交易数据的签名与签名子块中的签名进行对比验证，如果验证通过，则认可数据删除行为的合法性。

最后，本文对生成和删除区块的效率进行了分析。如第4.3节所述，本文需要选定合适的阈值，以权衡“门限环签名效率”“节省用户存储空间”以及“删除操作是否代表大多数节点的意见”这3点，使其在保障安全性的前提下也保证方案效率，其中，效率分析包括计算时间与存储空间比较，即删除操作用时越短，环签名所占空间越小，方案效率越高。在以下实验中，本文选取不同阈值，从“删除区块时间”和“删除后节省空间占比”这2个方面进行了比较。

图6 求解程序运行

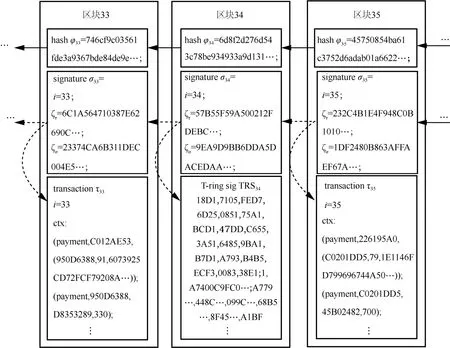
图7 区块34交易数据删除后区块33～35的数据

如第3.1节所述，对于所有的整数n和t，且t＜n，(n,t+1)-完备拆分系统一定是存在的。同时，为了使删除操作代表系统多数节点意见以保证安全，签名节点应在半数以上。以上实验中n=8，因此t={1,2,3}，合法阈值集合n-t={5,6,7}。表3和表4分别比较了不同阈值下区块删除的平均时间和删除前后的存储空间及节省空间占比。

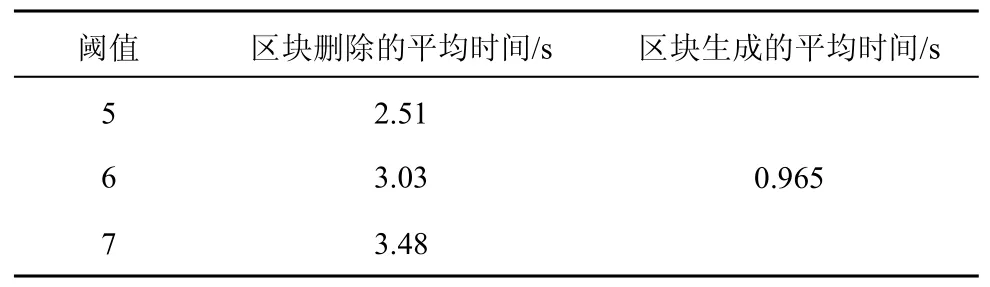
表3 不同阈值下区块删除的平均时间比较

表4 不同阈值下交易删除前后的存储空间及节省空间占比

由表3可知，区块删除的平均时间随着阈值的增大而增加，三者之间两两相差大约0.5 s，约占区块生成平均时间的对计算效率影响明显。由表4可知，当阈值为6和7时，交易删除后节省空间的效果显著，均大于80%；而阈值为5时，交易删除后节省空间大约60%。因此，当阈值为7时，虽然删除后节省空间的效果最优，但删除区块耗时较长；当阈值为5时，虽然删除区块耗时较短，但节省空间效果不太理想，且参与删除的节点相对较少，降低了方案的安全性。综合考虑区块删除的安全性和效率，本文选择阈值为6，即占比是同时保证方案安全性和效率的最佳阈值。

如表5所示，当阈值比例为75%时，生成一个区块平均耗时0.965 s，删除交易数据并生成门限环签名平均耗时3.028 s。

表5 5个区块在阈值比例为75%时的生成区块和删除区块耗时

5 结束语

本文首先提出了改进的门限环签名方案，在随机预言模型中可证安全，同时满足签名的强不可伪造性与签名者的匿名性。然后，基于空间证明的区块链结构，使用门限环签名方案提出了可删除的区块链。当某个区块数据过期失去存储价值时，经大多数节点同意后可有效删除该区块，大大节省了用户的存储空间，并保持区块链的总体结构不变。实验结果表明，所提区块链方案生成和删除区块的效率都很高，且不影响其他区块的存储和使用。