联合功率与信道的WSN生命期优化博弈算法

郝晓辰，姚宁,2，解力霞，王姣姣，王立元

（1. 燕山大学电气工程学院，河北 秦皇岛 066004；2. 北京交通大学海滨学院，河北 黄骅 061199）

1 引言

在物联网环境下，无线传感器网络（WSN,wireless sensor network）作为连接物理世界与信息世界的重要技术，已广泛应用于智慧交通等领域。WSN节点通过感知、处理和传输数据给观察者，实现相关智能应用[1]。然而该过程具有较大能耗，且电池作为主要的供电设备，其有限的供电能力使WSN寿命有限，因此在设计网络时应优先考虑减少节点能耗。同时，如果缺乏对信道的合理分配，节点间干扰过高时将导致数据传输失败，降低WSN的通信质量，并且，由于干扰使节点数据重传，从而增大额外能耗、加速节点失效、降低网络正常工作时间。因此，对于能量受限的 WSN，如何有效地利用节点能量减少节点间通信干扰、延长网络生命期，已成为亟待解决的关键问题。

降低节点能耗、减少节点间的通信干扰，是功率与信道资源分配的关键与目的。在WSN中，当节点失效时，网络的信息会重新分配，邻居节点会将其负载分配给邻近节点，这样会直接增加邻近节点的负载，造成其过早失效。因此，仅考虑节点的剩余能量并不能有效地延长网络生命周期，应充分考虑各节点及其邻居节点的剩余能量，同时考虑节点干扰对网络生命期的影响。

其次，功率与信道具有复杂的交互关系：一方面，信道分配受功率控制影响，拓扑中节点的功率不同，最优信道也不同；另一方面，功率控制与信道状态也密切相关，不同信道使网络节点的传输功率也不同。双方相互影响，相互制约，共同决定网络性能，这种特性和博弈较为相似[2]。

综上分析，本文首先利用网络拓扑信息和物理干扰模型构建节点的干扰模型，从而充分考虑节点的剩余能量及节点干扰对网络生命期的影响规律，构建网络生命期模型。进而引入势场博弈，通过分析WSN中节点能量与邻居节点剩余能量、节点发射功率与网络干扰、网络生命期之间的关系，构建联合功率与信道的 WSN生命期优化博弈算法（LOAPC, lifetime optimization game algorithm combined power and channel），有效实现功率和信道联合优化网络生命期的效果。

本文的主要贡献如下。

1) 结合网络的拓扑信息，运用物理干扰模型，充分考虑节点剩余能量对节点干扰及节点生存时间的影响，构建节点的干扰影响度量模型。

2) 采用节点期望传输次数，探索节点干扰对能耗的影响，设计新颖的节点能耗模型，并基于此模型构建节点的生命期模型，反映节点生命期与干扰、剩余能量及期望传输次数间的相互影响关系。

3) 基于节点的干扰影响度量模型及生命期模型，结合最佳回应策略，设计联合功率与信道的WSN生命期优化博弈算法。该算法运用信干噪比对节点的功率集合进行限制，减小算法计算量，并理论证明了该算法可收敛到帕累托最优。

4) 仿真结果表明，LOAPC具有较小的能耗与干扰，可以有效延长网络生命期。

2 相关工作

随着物联网的快速发展，人们对WSN的各项应用，如智慧农业[3]等的功能需求日益增多。此时WSN不仅面临着巨大的数据处理与传输带来的大量能耗，还面临着因通信干扰而日益加重的重传能耗，最终大大缩短网络生命期，因此，如何降低能耗与干扰进而提高网络生命周期，始终是资源受限的WSN亟待解决的热点问题。

为有效降低网络能耗，文献[4-5]采用拓扑控制方法尽可能地减小节点的发射功率，从而降低网络的传输能耗。然而降低能耗无法有效延长网络生命期，其忽略了节点剩余能量对生命期的影响，无法确保网络的正常工作时间。针对此问题，文献[6]提出了一种分布式的能耗均衡拓扑控制算法，该算法运用网络连通因子，利用剩余能量与初始能量的比值构建效益函数，在保证网络连通的前提下减小能耗，并使节点尽量选择剩余能量多的节点作为其邻居节点，最大化网络生命期。文献[7]同样以保证网络连通为基础，引入代数连通度，结合博弈理论构建能量效率的拓扑控制算法，以有效延长网络生命期。文献[8]以降低能耗与延长生命期为目标提出EETCA（energy efficient topology control algorithm），该算法以链路总能耗为链路权重，通过删除网络中能耗较大的链路，实现优化目标。

然而上述算法均未考虑网络的干扰情况，节点的发射功率在影响拓扑结构与能耗的同时，也影响着网络遭受干扰的程度。发射功率越大，节点的干扰范围越大，且距离发射节点越近的节点受到的干扰越大。信道分配是降低网络干扰的有效手段，因此，Chen等[2]提出了经典的信道分配（GBCA, game based channel allocation）算法，该算法综合考虑网络拓扑结构，以最小化节点间所造成及遭受的干扰为优化目标，有效降低了网络干扰，从而降低了能耗。然而该算法仅从信道角度降低干扰，减小能耗，忽略了剩余能量对二者的影响，因此 CAGLO（channel allocation game algorithm for anti-interference and lifetime optimization）[9]在 GBCA算法的基础上，运用节点剩余能量，构建生命期模型，以最大化网络生命期、最小化网络干扰为优化目标进行信道分配，从而最大化网络生存时间。但是该算法在固定的拓扑信息中构建模型，而实际上节点功率随着节点状态的改变而改变，从而使网络拓扑发生变化。为改善该问题，王东等[10]提出了三维拓扑（OVFSS, optimization variable fault-tolerant spanning subgraph）算法，使优化目标可随应用环境的通信情况进行调整，达到降低干扰与能耗、提高网络容错的效果。然而三维拓扑模型多应用于水下 WSN，此时通信模型将随之改变。为解决功率拓扑变化的问题，文献[11-13]提出了动态信道分配算法，然而该类算法具有较大的数据处理与通信能耗，并不适用于能量与计算能力受限的WSN。

为了有效地减小网络干扰与能耗，延长网络生存时间，研究者们采用多资源多目标协同优化的方法提升网络性能。例如，Liu等[14]提出了 MPCOSM（multi-performance cooperative optimization with self-maintaining）算法，该算法以网络连通、传输功率、剩余能量均衡、节点度及网络干扰为优化目标，构建多目标优化的效益函数，实现网络多性能的协同优化。Hao等[15]运用功率与信道的协同优化，结合信道间隔与中继传输对网络干扰及能耗的影响，提出了JACIRT（joint game algorithm of power control and channel allocation considering channel interval and relay transmission）算法。但是上述算法均具有较高的算法复杂度。JCPGC（joint channel allocation and power control optimal game-theoretic algorithm for concurrent transmission）算法[16]充分考虑功率控制与信道分配的内在关联性，设计了支持并行传输的联合功率与信道分配算法，很好地提升了网络容量并延长了网络的生命期，但是该算法没有考虑网络能量的影响，这对能量有限的WSN是一个很大的挑战。

基于上述分析，本文建立了联合功率与信道的生命期优化博弈模型（LOGMPC, lifetime optimization game model combined power and channel），在该模型的基础上设计了LOAPC优化算法。该算法不仅可以收敛到帕累托最优，且具有较小的算法复杂度，能有效减小网络能耗与干扰，延长网络生命期。

3 LOGMPC构建与分析

为保障WSN正常工作，不仅要求网络具有较低的干扰，确保信息服务质量，还要求WSN具有较长的网络生命期，确保物联网相关应用正常运行。在WSN中，网络生命期通常取决于节点的剩余能量和节点单位能量消耗。因此，本节首先考虑干扰、功率、能量等因素构建节点干扰模型，并在此基础上引入节点期望传输次数的概念，构建新颖的节点能耗模型。其次，结合节点剩余能量与能耗，设计节点生命期模型。最后，利用博弈论构建LOGMPC，保障WSN的生存时间，并通过模型分析证明LOGMPC具有稳定解。

3.1 干扰影响度量模型的构建

WSN干扰的大小通常由协议干扰模型和物理干扰模型来度量，其中，物理干扰模型采用节点功率与节点间距离来定量分析节点干扰，如式(1)所示，即节点i所遭受的干扰Ri为

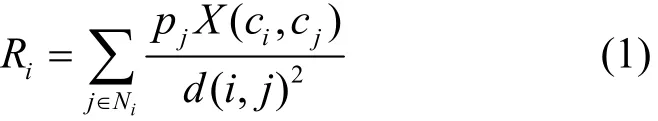
其中，Ni为节点i通信范围内的节点集合；pj为节点j的功率；ci、cj分别表示节点i、节点j此时所使用的信道；X(ci,cj)为节点i和节点j之间是否存在干扰的判断因子，且满足为节点i和节点j间的距离。

目前，由于电池作为WSN主要的供电设备，能量无法补充，且对于剩余能量较小的节点而言，若其能耗较大，将加速该节点的死亡，因此在信道分配时应优先考虑剩余能量较小的节点。同时，也要避免与剩余能量较小的节点分配同一信道，以免遭受较大的干扰，从而增加能耗，加速死亡。故本节将节点邻居剩余能量考虑到节点的干扰影响模型中，定义 WSN中任意节点i所遭受干扰的影响值Esi为

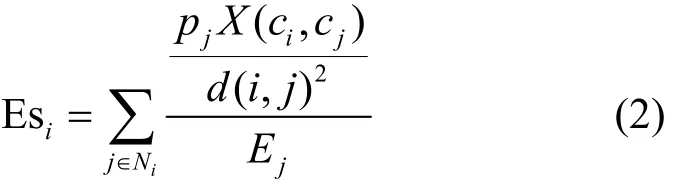
其中，Ej为节点j的剩余能量。

式(2)表明，当与节点i使用相同信道的邻居节点个数越多、功率越大且距离越短时，节点i遭受的干扰越大，重传能耗越多，从而越早失效，并且此时更应避免与剩余能量小的节点j使用同一信道（避免加重剩余能量小的节点的干扰）。因此，这种情况下节点i所遭受的干扰造成的影响Esi越大。

同时，节点自身所产生的干扰带来的影响 Eci也应考虑在内，因此得出节点i的干扰影响度量模型如式(3)所示。

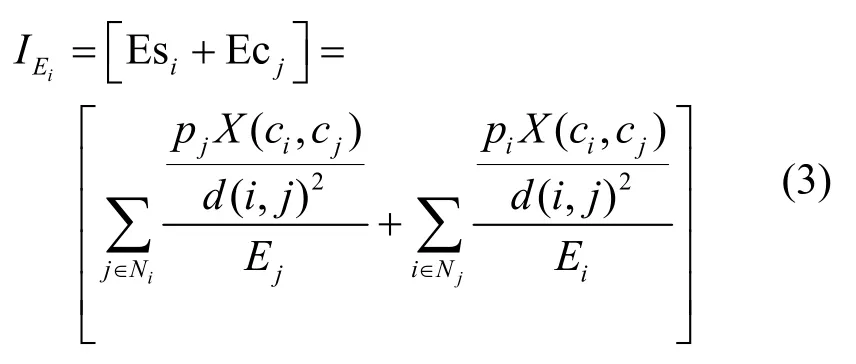
由式(3)可得，降低IEi的值，即降低节点i的干扰影响程度，不仅保护了剩余能量较小的节点自身，也保护了其通信范围内剩余能量较小的节点。

3.2 生命期模型的构建

1) 节点能耗模型

节点能耗的大小不仅取决于节点发送/接收数据量的大小，还与节点传输该信息的次数有关，所以节点由于干扰重传数据，加剧了节点的能耗。而根据IEEE 802.15.4协议要求，节点对之间每条路径的期望传输次数ETN不超过5[17]，即i与j之间的期望传输次数其中，SINRj是节点j的信干噪比（SINR, signal to interference plus noise ratio），f表示数据分组长度，且f＞ 0。因此当ETN(i,j)＞5时，则认为节点i与节点j之间不能相互通信。

本节采用较为简单并通用的一阶无线电通信能耗模型计算节点能量损耗。假设节点i周围有ni个邻居节点，每轮数据收集中每个节点产生lbit的消息，则节点i接收到的信息量为rRSi=节点i向节点j发送的信息量为假设节点接收和发送1 bit信息所耗能量分别为Er和Et，则在每轮数据收集过程中，节点i发送和接收lbit数据时的能耗为

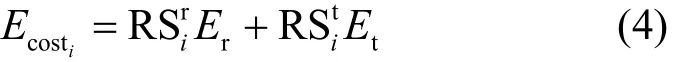
同时，在信息传输过程中，若节点干扰过大，将导致节点重新发送该数据分组。此时，设节点的干扰阈值为Rth（由后续 SINRth的值确定该参数的取值），节点干扰超过Rth越多，即越大，则该节点重传的概率就越大。与此同时，当任一节点j的初始能量E0(j)较小，而其能耗较大，即越大时，该节点提前死亡的概率就越大，此时失效的节点j就会将其负载分配给其邻居节点Nj，从而加重Nj的负载，进一步加重Nj的能耗。

综上分析，考虑节点干扰与负载重分配对节点能耗的影响，式(4)可转换为

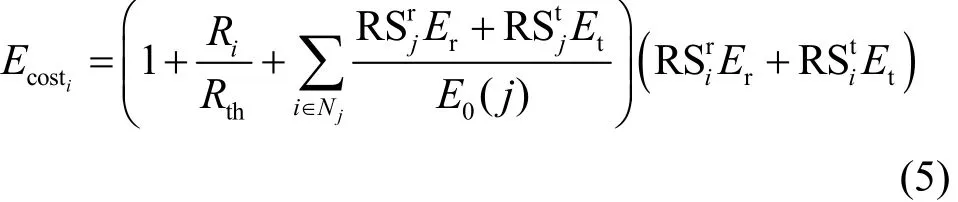
2) 节点生命期模型

由文献[9]可知，通常情况下，网络中任一节点i的生命期有关。然而，若其邻居节点因剩余能量较小而提前死亡时，一方面网络的连通性、覆盖率等将受到影响；另一方面将引发负载重分配从而增加节点i的能耗，降低网络生命期。因此节点i的生命期Tnode(i)不仅与Ei和Ecosti有关，还与其邻居节点j的Ej相关，故构建WSN中任意节点i的生命期模型Tnode(i)为

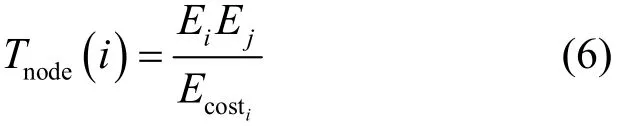
3.3 LOGMPC的构建

博弈模型主要由参与者、策略空间和效益函数三要素构成，在此，本文分别从该三要素对降低干扰和节点能耗的LOGMPC进行具体描述。

1) 参与者I

2) 策略空间S

接收节点j的信干噪比[16]SINRj为

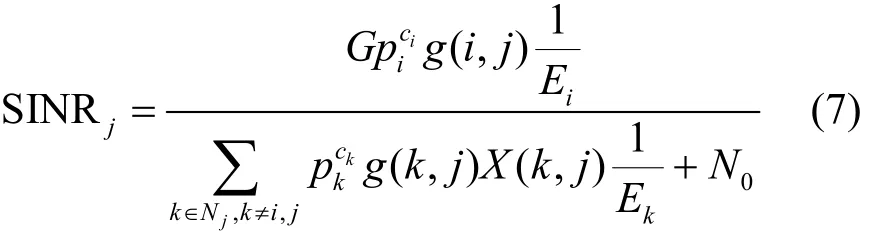
其中，G为发射节点放大器的处理增益，为点i在信道为ci的发射功率，为节点i和节点j之间的路径增益，N0为噪声干扰。当接收节点j的信干噪比高于信干噪比阈值 SINRth（即SINRj≥SINRth）时，节点才可以成功接收信息。将式(7)代入 SINRj≥SINRth，解得节点i的最小发射功率为

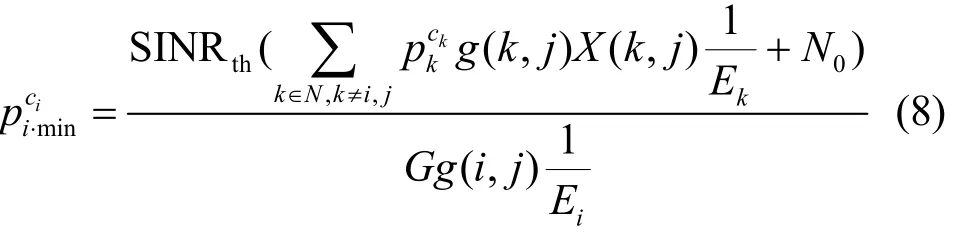
而节点i在信道ci中会存在很多邻居节点与其共用同一信道，因此i应尽可能地调节自身的功率大小以保证不影响信道中除节点i以外的其余任意节点m(m≠i)的数据传输。对于网络中任意节点m来说，同样需要节点m的信干噪比高于SINRth时，才能成功地接收信息，将节点m的信干噪比公式代入不等式SINRm≥SINRth，有

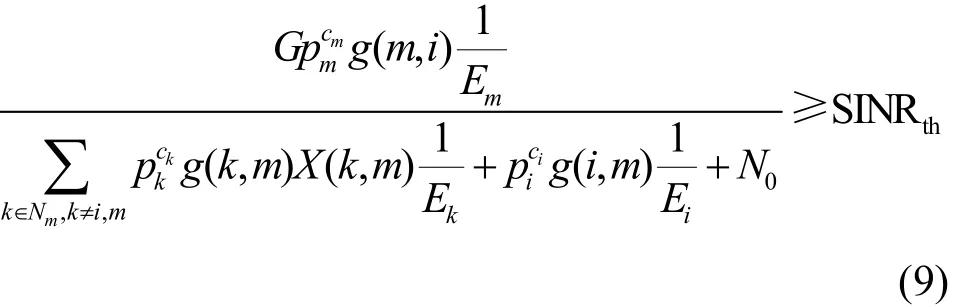
由式(9)解得此时节点i功率的最大值为

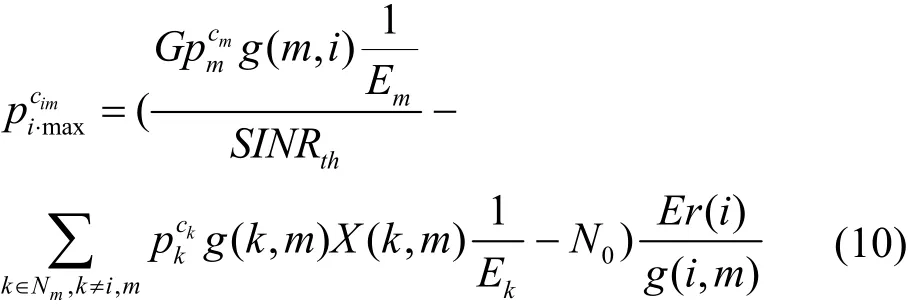
由于节点有最大功率pmax的限制，经以上分析，取节点的为

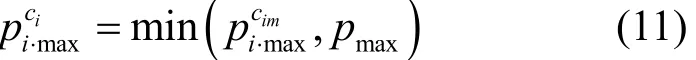
结合上述计算可得节点i的可选功率集合为

3) 效益函数u

参与者I在策略组合下所得到的效益用表示，所有参与者的效益集合为

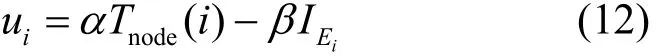
综上所述，考虑节点的干扰影响度量模型和生命期模型，定义生命期优化博弈模型的效益函数ui为其中，α和β为非负的网络生命期模型和节点干扰影响度量模型的数量级均衡因子，因此，本文设定α=1×10-7，β=1×10-3。

由式(12)可得，当最大化ui时，将最大化节点的生命期与最小化节点的干扰影响，从而达到减小干扰、延长网络生命期的效果。

3.4 LOGMPC特性分析

对于博弈论而言，纳什均衡是博弈模型的稳定解。同时，对于势场博弈而言，使势场函数达到最大值时的策略组合即为该博弈的纳什均衡解。故本节将基于势场博弈相关理论，证明LOGMPC存在稳定纳什均衡解。

性质1 LOGMPC是势场博弈

证明 要证明 LOGMPC博弈模型是势场博弈，只需证明其存在势场函数V，满足势场函数的变化值ΔV和节点选择不同策略时效益函数的差值Δui保持同号即可。由效益函数公式可以构造势场函数V(p,c)为

当节点i的功率和信道由时，i的效益改变量为

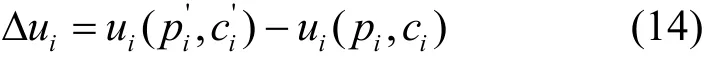
式(13)的势场函数的变化值ΔV为

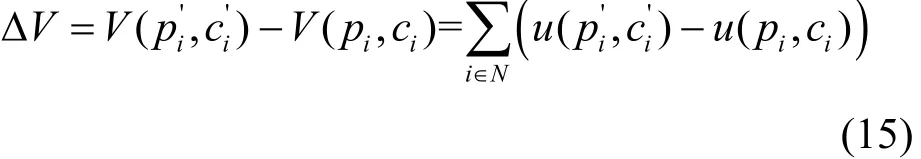
式(15)的势场函数的改变值ΔV可以分为2个部分：1)对于网络中任意节点(j≠i,j∈N)的效益函数改变量之和；2)节点i的效益改变量。因此可以得到

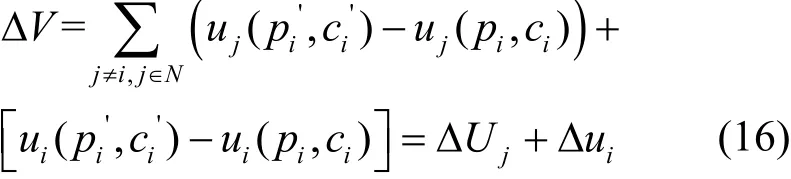
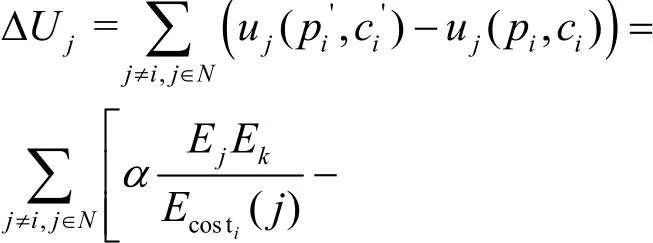
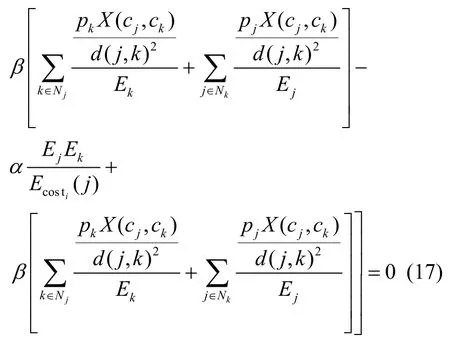
将式(17)代入式(16)可得

因此，LOGMPC存在势场函数使ΔV与Δui同号，故LOGMPC博弈模型是一个势场博弈。

性质2 LOGMPC存在至少一个纳什均衡解。

证明 在性质1的证明过程中，已经证得如式(13)所示的函数V(p,c)是LOGMPC博弈模型的势场函数。而网络中任意节点的功率和信道都是有限的，所以在LOGMPC的策略空间中，必然存在一个策略组合使其相应的势场函数V(p,c)达到最大值。而最大化V(p,c)的策略组合即为LOGMPC博弈模型的纳什均衡解，因此LOGMPC博弈模型存在至少一个纳什均衡解。

4 LOAPC设计与分析

在本节中，基于3.3节所构建的生命期优化博弈模型LOGMPC，运用最佳回应策略设计LOAPC博弈算法，并理论证明LOAPC能够收敛到全局最优的帕累托状态。

4.1 生命期优化博弈算法设计

LOAPC首先使节点广播信息，从而完成节点的信息收集，构建自己的邻居列表。

构建完邻居列表后，节点基于最佳回应策略进行博弈，计算不同信道与功率下节点的效益值，从而选择效益值最大的信道与功率作为自己本轮的策略。当网络中所有节点的策略与上一轮中所选择的策略相同时，即达到纳什均衡状态，博弈结束。

在算法的博弈阶段，优先给剩余能量较低的节点分配信道和功率，避免后期与其他节点分配到同一信道。在第t轮博弈时，若节点允许更新策略时，首先降低节点的一个功率，并判断此时网络是否连通。若网络不连通，则节点功率重置为t-1轮的功率值；若网络连通，则在此功率下根据效益函数式(12)计算节点在不同信道下的效益函数，并基于最佳响应策略选择最大效益值对应的节点发射功率等级以及信道。依次更新其他节点的功率和信道策略，当网络中所有节点都更新完，判断此时算法是否达到纳什均衡，如果达到纳什均衡状态，则算法结束，否则，继续参与下一轮循环。

4.2 生命期优化博弈算法性能分析

性质3 LOAPC能够收敛到纳什均衡。

证明 由势场博弈相关理论可知，使V最大化时的信道与功率状态即为该博弈的纳什均衡解。而当LOAPC基于最佳回应策略使各节点选择使效益值最大化的信道和功率时，WSN中各节点效益总和必然也是最大的，因此 LOAPC能够收敛到纳什均衡。

虽然LOAPC可以收敛到纳什均衡状态，然而该纳什均衡可能是局部最优解。为证明所构建的LOAPC最终可收敛到全局最优，只需证明其收敛到的纳什均衡是帕累托最优即可，因此引入帕累托最优概念。

定义1 帕累托最优[18]。对于任意i∈N，若不存在策略s∈S，使成立，则s*即为该博弈模型的帕累托最优。

性质4 LOAPC能够收敛到帕累托最优状态。

证明 根据纳什均衡定义，在WSN中不存在节点通过降低自身的发射功率和信道选择来得到更高的效益，如果每个节点功率持续改变，则可能会影响整个网络的连通性。其次，在保证WSN连通的前提下，不存在k(k≥2)个节点同时通过降低功率来实现自身效益的增加。每个网络中的节点如果通过相对应的方法降低了自身的功率，则会导致网络不连通，那么与之相邻的节点就会同时增加功率去保证网络的连通性，如此一来网络中其他节点的效益就会降低，更何况k个邻居节点同时增大自身收益。故可得LOAPC博弈算法最终可达到帕累托最优状态。

5 仿真实验

LOAPC与 CAGLO[9]的应用场景均为平面型WSN，且LOAPC相较于CAGLO同样考虑了干扰、能耗及生命期对网络性能的影响并进行了改进。此外，CAGLO在构建相应的干扰、能耗、生命期指标及博弈模型效益函数时，忽略了节点功率对网络各性能的影响。因此，为验证LOAPC的有效性，本文选取优化目标相同的CAGLO作为对比算法，从多个性能方面进行仿真，证明LOAPC在降低干扰与延长生命期等方面的功效。在该仿真中，使100个节点随机分布在500 m×500 m的监测区域内，具体仿真参数如表1所示。

表1 仿真参数

1) 网络节点平均干扰

设置网络信道数为5，改变节点数为60～110，步长为10，计算节点平均干扰，即网络中所有节点干扰的平均值，如图1所示。

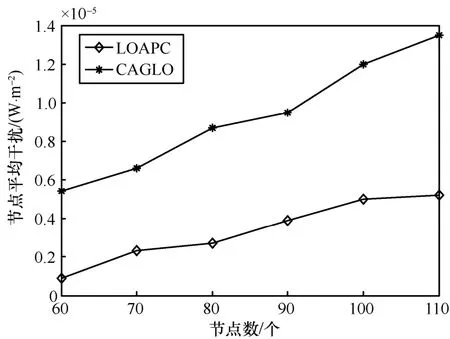
图1 网络节点平均干扰对比

由图1可知，随着节点数的增加，LOAPC与CAGLO下的节点平均干扰逐渐增大，但 LOAPC下的干扰始终小于 CAGLO，且增加缓慢。这是因为随着节点数的增加，节点间的距离减小，同时使用相同信道的节点增加，因此干扰呈增长趋势。并且LOAPC考虑功率影响因素，适当调整功率，因此相较于CAGLO而言，能有效降低网络节点的平均干扰。

2) 网络节点平均功率

设置可用信道个数为5～10，步长为1，分别利用LOAPC和CAGLO计算不同可用信道数时网络中所有节点发射功率的平均值，如图2所示。

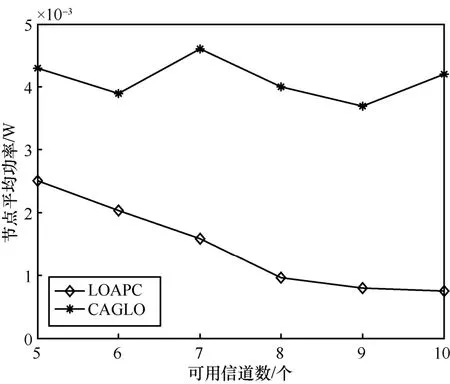
图2 网络节点平均功率对比

由图2可知，LOAPC下的节点平均功率随着信道个数的增加而逐渐降低，且小于 CAGLO，有效节约了节点能量。这是因为LOAPC在信道分配的同时合理地调节节点的功率大小，在保证网络连通的情况下最小化节点的功率，有效地减少了网络的能耗。而CAGLO并未考虑节点功率，因此其平均功率为网络初始化功率，较为稳定，在一定范围内波动。

3) 网络生命期

网络生命期对比如图3所示。由图3可知，LOAPC的生命期始终大于CAGLO，可以有效延长网络生命期。这是因为 LOAPC将节点剩余能量及功率对生命期的影响均考虑在内。同时，由图 2可以看出，CAGLO下的节点的功率均大于LOAPC，故CAGLO下的各节点的邻居节点数普遍大于LOAPC。由式(4)及式(6)可得，CAGLO下的生命期低于LOAPC。在图3中，虽然LOAPC下的网络生命期随节点数目的增多大体呈减少趋势，但在节点数为70～90时，网络生命期出现波动。这是因为当网络中的节点数增多时，在保证网络连通及降低能耗的原则下，节点功率降低，各节点间距离减小。因此，由式(7)可知，随着网络中节点数的增多，各节点的信干噪比可能增大也可能减小，所以随着节点数的增多，网络的生命期可以增大也可以减小，造成节点数在 70～90时，生命期出现上下波动的情况。而当节点数为100和 110时，由于信道数的有限性，使网络中使用相同信道的节点对增多，从而降低网络生命期，因此其呈下降趋势。

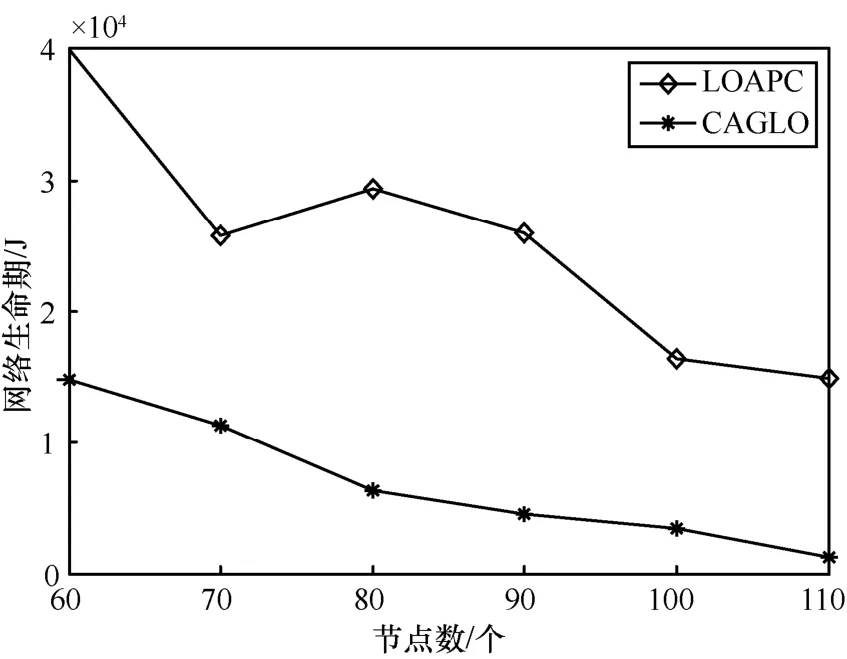
图3 网络生命期对比

4) 网络收敛性

用算法的收敛速度来度量算法的复杂度，即算法的收敛速度越快，算法本身的复杂度越低。收敛轮数对比如图4所示。

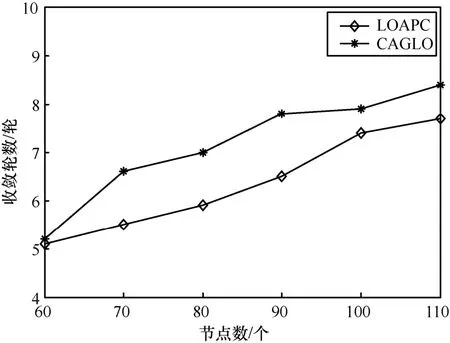
图4 收敛轮数对比

由图4可知，LOAPC的收敛轮数低于CAGLO。这是因为LOAPC不仅在博弈阶段考虑节点的剩余能量，优先为能量小的节点分配功率与信道，加快博弈收敛速度，还通过约束节点功率，降低了算法的计算量。因此，LOAPC收敛速度更快，算法复杂度更低。

6 结束语

为了优化网络资源，本文从降低网络能耗与干扰入手，构建了新颖的干扰影响度量模型、能耗模型及生命期模型，量化了网络能耗及干扰对网络带来的影响，并在此基础上充分考虑上述三者间的交互作用，构建了LOGMPC博弈模型。其次，基于LOGMPC，本文以优化网络生命期为目标，设计了联合功率与信道分配的WSN生命期优化博弈算法LOAPC。理论分析表明，LOAPC可以实现帕累托纳什均衡。最后，通过算法对比仿真实验，得出本文所构建的 LOAPC在节约节点能量、降低节点干扰等方面显示出较大的优势，且具有较快的收敛速度，在降低网络能耗的同时延长了网络的生命期。