仿半叉迹特征的快速分形图像编码

2019-05-05张爱华纪海峰

小型微型计算机系统 2019年4期

赵敏，张爱华，纪海峰

(南京邮电大学理学院，南京 210023)

1 引言

1988年Barnsley在对迭代函数系统[1]研究的基础上，首次提出了分形图像编码.虽然文献[1]取得了非常高的压缩比，但编码所消耗的时间过长，并且还需要人机交互，因而它的适用性较弱.1992年Barnsley的博士生Jacquin提出了分形块编码[2]，其理论基础是分块迭代函数系统PIFS(Partitioned IFS)，它可以在计算机上自动实现全搜索分形编码算法.虽然能实现图像数据的高倍压缩，但耗时长，复杂度高.因此，近二十年来，针对这个问题人们提出了许多加快编码的方法[3-9].在快速分形编码方法中，广泛使用特征向量法[10]，其原理是“d(φR，φD)≤δ⟺MSE(R，D)≤ε”.所以怎样选取合适的特征向量使它能整体的反应图像块信息，以及不会使维数过高是其问题的关键.不少研究者为了有效提高编码性能，从而定义一个图像块的新特征[11-15].文献[12]提出主成分的子块特征，[13]提出主对角和的子块特征，[16]四线和的子块特征，都不同程度提高了编码性能.在此基础上，本文选取规范块图像子块，先给出仿半叉迹的定义，其次选取其上的像素点的灰度值作为特征点，在理论上给出：文中所选特征与MSE(均方根度量)关系的证明，建立了匹配子块间的仿半叉迹特征搜索终止条件[16].仿真实验结果表明本文提出的仿半叉迹特征的快速分形图像编码是有效的，优于文献[16]中的算法和基本分形编码算法，达到既加快了编码时间，又降低了计算复杂度的目的.

2 仿半叉迹特征的快速编码方法

2.1 理论基础

定义1.规范化的图像块X=(xi，j)B×B定义为

(1)

定义2.图像块X=(xi，j)B×B的仿半叉迹定义为

定理. 设R，D∈RB×B，则下面不等式成立：

(2)

证明:定义子块Q=(qi，j)∈RB×B如下：

对于子块X=(xi，j)，记X=(xi，j).根据定义1和定义2有

(3)

参数s和ο，由以下公式确定

(4)

(5)

又结合式(4)，则匹配误差为

即对于非平滑块R，得到其匹配误差与仿半叉迹特征的关系

定理证毕.

2.2 算法描述

本文算法的具体步骤如下：

1)将原图像分割成B×B的固定块，记为R块；

2)设定R块的标准差阈值τ和计算σR；

3)在横竖方向上，以δ为步长，得到2B×2B的D块，即在相邻D块间，会有δ个像素在水平方向或垂直方向发生重叠.然后，对每个D块，采用4-邻域像素[5]的方法，平均得到B×B块，得到的子块构成集合码本Ω；

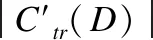
5)对于每个R块，搜索最佳匹配块Dm∈Ω：

(ii)如果σRi≥τ，则按二分法[7]在Ω′中搜索初始匹配快Dm；

7)对于剩下的R块，重复步骤5)和步骤6).

图1 算法的整体流程图Fig.1 Overall flow diagram of the algorithm

上述算法流程图如图1所示.

3 实验结果分析

为验证仿半叉迹算法的编码效果，实验对象为4幅复杂性不同的512×512×8bit标准测试图像Lena，man，peppers和milk drop.图像采用一致方块分割，选取R块大小为8×8，D块大小为16×16，步长δ=16.实验在Windows旗舰版操作系统(2.50GH i5-3210M CPU/4GB内存)上进行，程序用Matlab r2012b编写，测试参数为编码时间(t)，峰值信噪比PSNR(dB)和结构相似度SSIM.

由文献[6]可知，仿半叉迹算法的编码时间和解码图像质量依赖于三个控制参数：R块的标准差阈值τ，D块的标准差阈值η和邻域k.阈值参数τ越大，被当做常值块的子块R就越多，虽然编码速度会加快，但是解码图像质量会降低.文献[11，13]的仿真实验表明，当τ≤4，块效应基本消失，码本块的标准差阈值η的取值范围为20与35之间为宜，因此，在本实验中，τ取3，η取30为默认值.在相同的实验条件下，文中仿半叉迹特征算法与1-范数算法、基本分形算法的对比结果列于表1；与四线和特征算法的对比结果列于表2.

从表1可以得出当k≥5时，以PSNR度量的解码图像质量，本文算法优于1-范数算法，且时间和SSIM(图像结构相似度)也没多大偏差；与基本算法相比，当k=30时，在PSNR值下降约1.37dB的情况下，本文编码速度平均加快了23倍左右，此时，图像的SSIM保持在99.9%.即文中算法可以在保证一定图像质量和结构相似度的前提下，大幅度提高编码速度.例如在实时性要求高，质量次之的应用场合，可选取较小的k值.随着k的不断增大，两个算法的编码性能趋于相同.由文献[14]知因为局部匹配块代替全局匹配块产生的误差通常会随着k值的增大而减小.因此，当k足够大时，这种误差就会小于误差阈值，误差阈值就失去了作用，落在搜索半径内的最佳匹配块不在增加.

表1 不同算法在K取不同值时对Lena编码的结果Table 1 Results of three different encoding algorithms for Lena

图2给出了Lena，man和peppers在本文算法和1-范数特征算法下的“PSNR——时间”图，图中数据分别取这两种算法在不同邻域k(k=1，5，10，…，200)下得到的PSNR和相应的时间t.图2表明，在相同邻域k下，本文算法在编码时间比1-范数算法耗时略多，但相应的PSNR优于它，同样也可以看出，在相同的PSNR下，本文算法比1-范数算法耗时略少.因此，仿半叉迹特征算法较优.