动态随机树贝叶斯集成回归模型研究

王双成,郑 飞,唐晓清

1(上海立信会计金融学院 信息管理学院,上海 201620)2(上海立信会计金融学院 统计与数学学院,上海 201620)

1 引 言

虽然贝叶斯网络(Bayesian networks)[1]在许多领域得到了广泛的应用,但不能直接使用贝叶斯网络处理时间序列问题(这种问题在宏观经济、金融和管理等领域普遍存在).动态贝叶斯网络(dynamic Bayesian networks)[2]是贝叶斯网络与马尔科夫链(Markov chain)的结合,在概率框架下能够实现动态(时序)和静态(非时序)信息的融合,可用于动态分析、预测和控制等.

目前,对动态贝叶斯网络的研究主要集中在动态贝叶斯网络学习和推理,减弱平稳性与马尔可夫性假设,以及动态贝叶斯网络的应用方面,如Lähdesmäki[3],Robinson[4],倪小虹[5],Jonas[6]和Xiao[7]等的动态贝叶斯网络结构与参数学习研究,王浩[8],Dondelinger[9],Gao[10]和Komurlu[11]等的动态贝叶斯网络推理研究,以及杜友田[12],Ontaón[13],Cai[14],王双成[15,16]和吴非[17]等的动态贝叶斯网络应用研究(包括动态贝叶斯网络分类器)等,还缺少将动态贝叶斯网络用于时间序列回归计算方面的研究.

在时间序列回归计算方面,以自回归移动平均(简记为ARIMA)模型和广义自回归条件异方差(简记为GARCH)模型最具代表性,但ARIMA和GARCH是一维时间序列回归模型,只能使用时间序列自身的时序信息,无法利用相关的其它时间序列所提供的信息.一些人工智能技术也被用于时间序列的回归计算,如神经网络、支持向量机和决策树等,这些模型能有效地利用其它相关时间序列所提供的非时序信息,但无法利用时序信息.

本文的主要贡献如下:

1)结合分类与回归之间的相互转换、类的满条件概率估计和以满条件概率为权重的加权平均回归计算等,在理论上给出了动态贝叶斯回归模型,并建立了动态贝叶斯衍生回归模型(由动态贝叶斯回归模型衍生的回归模型)体系结构,将为系统而深入地研究动态贝叶斯衍生回归模型奠定基础.

2)在动态贝叶斯回归模型的基础上,将动态随机树的生成、基于动态随机树的联合密度分解、属性密度估计和以满条件概率为权重的加权平均回归计算等相结合提出了连续属性动态随机树贝叶斯回归(dynamic random tree Bayesian regression,简记为DRTBR)模型.

3)通过DRTBR模型平均建立了动态随机树贝叶斯集成回归(dynamic random tree Bayesian ensemble regression,简记为DRTBER)模型,并在wind数据库中选择期货时间序列数据,对DRTBER模型的可靠性和实用性进行了实验验证与分析.

文章分为五个部分,第一部分是对动态贝叶斯网络和时间序列回归计算的发展进行回顾与分析;第二部分给出动态贝叶斯分类器和回归模型;第三部分建立DRTBER模型;第四部分是使用期货数据进行实验与分析;第五部分是结论和进一步的工作.

2 动态贝叶斯分类与回归

首先给出动态贝叶斯分类器,然后在动态贝叶斯分类器的基础上建立动态贝叶斯回归模型,最后构建动态贝叶斯衍生回归模型的体系结构.

2.1 动态贝叶斯分类器

分别用X1[t],X2[t],…,Xn[t],C[t](1≤t≤T)表示时间序列属性变量(简称为属性)和时间序列类变量(简称为类),x1[t],x2[t],…,xn[t]和c[t]是具体的取值,Dc[n,T]={x1[t],x2[t],…,xn[t],c[t]}(1≤t≤T)是具有T个记录的时间序列分类数据集.

依据贝叶斯网络理论和图 1(a)中所蕴含的条件独立性关系,可以得到:

p(c[t]|c[1],…,c[t-1],x1[1],…,xn[1],…,x1[t],

…,xn[t])=p(c[t]|c[t-1],x1[t],…,xn[t]).

定义1.称使用图1(a)结构(用S[t]表示)和公式(1)进行分类的分类器为动态贝叶斯分类器(Dynamic Bayesian classifier,简记为DBC).

(1)

DBC是一个基础概率分类器,由DBC可衍生一系列的分类器,可将这些分类器称为动态贝叶斯衍生分类器,细节参看文献[16].

2.2 动态贝叶斯回归模型

定义2.称使用图 1(b)结构(用R[t]表示)和公式(2)进行回归计算的模型为动态贝叶斯回归模型(Dynamic Bayesian regression model,简记为DBRM).

(2)

如同DBC一样,DBRM也是一个基础模型,由DBRM也可衍生出一系列的回归模型,我们将这些模型称为动态贝叶斯衍生回归模型,动态贝叶斯衍生回归模型的构成如图2所示.

图2 动态贝叶斯衍生回归模型的构成Fig.2 Composition of dynamic Bayesian derivative regression model

图2为系统而深入地研究动态贝叶斯衍生回归模型奠定了基础.本文研究一阶动态贝叶斯衍生回归模型,并通过模型平均进行优化.

3 动态随机树贝叶斯集成回归模型

虽然已有许多可用于时间序列回归计算的模型,但这些模型或者使用时序信息,或者使用非时序信息,不易实现二者的结合,而这两种信息均是回归计算的重要信息.DRTBER模型能够将时序与非时序信息有机结合,来提高回归计算的可靠性.建立DRTBER模型主要包括时间序列预处理、DRTBR计算和DRTBR集成三个部分.

3.1 时间序列预处理

时间序列预处理是建立回归模型的基础,包括丢失数据修复、规范化、回归变量的离散化和类变量的数量化.我们分别采用滑动平均法和差分法来修复丢失数据和去除单调性,还要对数据进行规范化,并基于等频离散化方法离散化回归变量(这种方法能够避免离散化可能出现的极端情况).通过回归变量的离散化,将连续的回归值转化为离散的类值,在这一过程中,一个类值代表一个回归值的集合,让类值与回归值集合的平均值相对应,来实现类变量的数量化.

3.2 DRTBR计算

DRTBR计算是建立DRTBER模型的核心,首先生成动态随机树,然后基于动态随机树分解条件概率,最终实现DRTBR计算.

1)动态随机树的产生

动态随机树的形成机制是:首先随机产生X1[t],X2[t],…,Xn[t]的一个排列Xu1[t],Xu2[t],…,Xun[t],然后在变量子集{Xu1[t],Xu2[t],…,Xuk-1[t]}中随机产生Xuk[t](k≠1)的父结点Πuk[t],便可形成一颗随机树.我们能够证明任何一棵属性树都可以采用这种方法生成.动态随机树的结构(用Tree[t]表示)如图3所示.

图3 动态随机树的结构Fig.3 Structure of dynamic random tree

2)基于动态随机树的条件概率分解计算

根据概率公式、贝叶斯网络理论和图3中变量之间的条件独立性关系,可以得到:

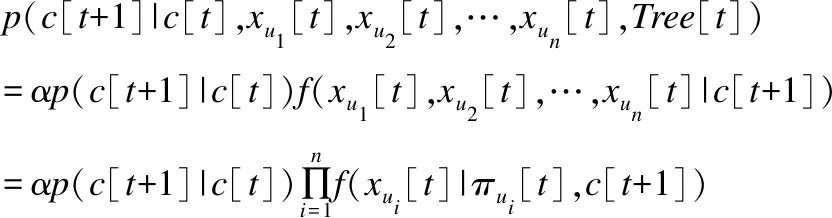
(3)

其中α是与C[t]无关的量,p(c[t+1]|c[t])是类转移概率,f(xui[t]|πui[t],c[t])是属性条件密度,πui[t]是Xui[t]的父结点Πui[t]的取值.

DRTBR模型可以表示为:

(4)

其中wh是条件概率权重,βh(1≤h≤H)是归一化系数.

3.3 DRTBR集成

随机产生M个随机树T(1),T(2),…,T(M),建立对应的M个回归模型,通过模型平均得到DRTBER模型.

DRTBER的集成结构如图4所示.

图4 DRTBER的集成结构Fig.4 Ensemble structure of DRTBER

DRTBER可以表示为:

(5)

y[T+1]的计算过程如算法1所示.

算法1.计算y[T+1]的算法.

(1)输入:x1[T],x2[T],…,xn[T],y[T]

(2)输出:y[T+1]

(3)回归变量的离散化,得到类变量C[t]

(5)FORm=1 toM

(7)END FOR

(8)模型平均计算

(9)加权回归计算,得到y[T+1]

在DRTBER的回归计算中,主要部分是计算子回归模型的条件概率权重,而条件概率权重计算的核心是属性条件密度估计,一个子回归模型的权重需要进行n次属性条件密度估计,H和M是与n无关的量,因此,相对于属性条件密度估计,DRTBER模型回归计算的时间复杂度是O(n).

3.4 属性密度估计

我们采用抗噪声能力强且泛化性能好的高斯函数来估计属性密度,具体情况如下:

(6)

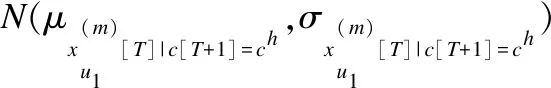
(7)

3.5 时序回归可靠性标准

(8)

其中G表示DRTBER,TSRR(T,Ω,G)越小DRTBER越可靠.

4 实验与分析

在Wind数据库中选择用于实验的期货时间序列,使用等频离散化的方法对回归变量进行离散化,基于高斯函数来估计属性密度,依据TSRR标准计算回归模型的误差,其中T=241,Ω=100,M=20,H=15(M和H是根据实验测试的经验值).

选择十个回归模型,它们分别是:滑动平均回归(MAR),动态朴素高斯回归(DNGR),超父结点高斯回归(SPNGR),动态随机链高斯回归(DRCGR),神经网络(NN),支持向量机(SVM),分类与回归树(CART),自回归移动平均(ARIMA),自回归条件异方差(GARCH),动态随机树贝叶斯集成回归(DRTBER).对DRTBER与其它回归模型进行回归误差的差异显著性检验[18],检验结果如表1所示.

我们能够从表1中发现,DRTBER的回归误差与其它回归模型的回归误差之间差异显著.在总体平均值方面,DRTBER优于其它回归模型的程度依次是:48.34%,41.50%,22.45%,26.50%,32.71%,20.948%,29.90%,29.44%和21.80%,DRTBER的优势明显,回归误差比较的直观显示散点图如图5所示.

表1 期货时间序列的回归误差实验结果
Table 1 Experimental results of regression errors in futures time series

时间序列数据集MARDNGRDRCGRSPNGRNNSVMCARTARIMAGARCHDRTBER收盘价_铜0.0045140.0093440.0036250.004180.0029030.005310.0089160.0071250.0061920.003582收盘价_银0.0123460.0147590.0106180.0114920.0096550.0049870.0065730.0116350.0129650.004876收盘价_铝0.008370.0030210.0065830.0068190.0068760.0074350.0058860.0059270.001740.001621收盘价_金0.0023750.0041690.0016320.0025380.0035320.0009870.0009770.011240.0016770.001514收盘价_燃料油0.0152320.0113580.0042350.0085660.0043690.0094250.0181230.0135270.0097710.006913收盘价_热轧卷板0.0161580.0082430.0143790.013640.0078410.014850.0193770.0108190.0086480.00687收盘价_镍0.0016610.0031460.0011340.0010520.0029090.0005670.0008730.0009610.0004280.000727收盘价_铅0.0051840.0072620.0086280.0078170.0059470.0031790.0033090.0090320.0028350.002545收盘价_铷0.0095230.0114170.0108950.0116340.0069290.0175650.015820.0125780.0076650.006382收盘价_钌0.0132620.0155460.0105810.0101920.0058970.0098110.0252730.0087950.0081860.008456收盘价_锡0.0080920.0093050.0228940.0232370.0030340.0012470.0026140.0021060.0024670.001683收盘价_线材0.0217710.0153630.0125070.014640.0158850.0206170.018960.0065840.0037010.003291收盘价_锌0.0181550.0122970.0107420.0113150.0062820.0140180.0116930.013620.0073420.006084涨跌_铜0.023070.0201480.0203370.0226350.0219790.0066740.0195620.0248260.0185890.023772涨跌_银0.0213610.0214460.0146650.0161140.0247780.0183560.0130490.022620.0221650.020576涨跌_铝0.0385350.0339920.0382030.0407710.0432850.0266040.0283340.0424170.0418830.036245涨跌_金0.0185890.0160230.007140.0083370.0070860.0031440.0053290.0092090.0051440.003028涨跌_热轧卷板0.0435280.0385270.0344560.0329130.0470180.0310250.0457210.0419850.0408710.038285涨跌_镍0.0378510.0394160.0171920.0182540.0306190.0163290.0348440.0212530.0270630.015814涨跌_铅0.0263740.0245450.0127180.0158920.0227010.0108860.016350.0138810.0119190.010583涨跌_铷0.0325360.0356340.026720.0286960.0466270.031210.0382640.027270.0252050.024356涨跌_钌0.028580.0302560.0165730.0172410.0303520.026050.0227990.0226350.0269330.014288涨跌_锡0.0244170.0133820.0189470.0193840.0363890.0145250.0232860.020620.0196960.017539涨跌_锌0.0274650.0287410.0213590.0235710.0339020.0197470.0225150.0224150.0252160.01806成交量_铜0.0195190.0182670.0108340.0149360.0032610.0160850.003540.0126320.0150610.003116

续表

从散点图中我们能够发现,在回归误差方面,DRTBER要明显优于其它的回归模型.回归误差的差异比较如表2所示.纵观上述实验结果,我们可以得出结论,DRTBER相对于其它九个回归模型在回归误差方面具有比较明显的优势.

表2 回归误差的差异比较
Table 2 Difference comparison of regression errors

5 结论和进一步的工作

给出了动态贝叶斯分类器与回归模型,以及动态贝叶斯衍生回归模型体系,在此基础上,将分类与回归之间的相互转换、加权平均回归计算和回归模型平均等相结合建立了用于时间序列回归计算的DRTBER模型,该模型能够在统一的概率框架下融合动态(时序)与静态(非时序)信息,并可有效利用属性之间的依赖信息来提高回归计算的可靠性,而不同回归模型之间的模型平均又有利于实现优势互补,进一步提高了模型的泛化能力.使用期货时间序列数据进行实验的结果显示,基于DRTBER模型的时间序列回归计算具有良好的可靠性和实用性.进一步的工作是提高DRTBER模型的计算效率,将其向高频大时间序列的回归计算扩展,以及高阶DRTBER模型的探索.