火星再入飞行器风洞试验与真实飞行之间相关性的探讨

2019-05-05刘方彬袁军娅

北京航空航天大学学报 2019年4期

刘方彬，袁军娅

(1. 北京航空航天大学宇航学院, 北京 100083； 2. 深圳易信科技股份有限公司, 深圳 518000)

火星大气的主要成分是CO2，大气非常稀薄，密度仅为地球大气的1%。相对于地球大气，再入飞行器进入火星大气时，虽然同样具有较高的飞行速度，但是由于火星大气密度较低，在高速飞行时激波后流动的热力学非平衡特性更为突出。作为火星大气主要成分的CO2气体，具有和N2、O2等气体不同的热化学特性[1]。目前对于火星再入飞行器实际飞行时，仍存在诸多认知上的不足，包括剪切层的复杂性、尺度问题和一些现象的物理模型等方面，地面试验仍是火星再入飞行器研制中必不可少的验证手段[2]。

由于风洞条件的限制，难以完全模拟飞行环境，且在风洞试验中有尺寸效应、边界效应或边界干扰、支架干扰等干扰，这就存在一个与真实飞行条件下的相似理论及相关性的问题。目前关于地球再入飞行器的风洞试验相关性研究较多，相似准则的选择也有多种，而关于火星探测器风洞试验相关性研究的国内外公开文献极少，且成熟度不高。例如苗文博等[1]则利用数值方法研究了火星再入飞行器表面热环境，通过研究认为，在驻点附近区域近似为热力学平衡，随着高度逐渐增加，则热力学非平衡效应更明显。董维中[3]在博士论文中根据钝锥标模ELECTRE模型风洞试验和飞行试验数据之间对比，认为保持总焓值不变，利用双尺度参数可以对模型头部进行气动热/力的外推。然而ELECTRE模型的试验介质均为空气，没有进行介质为CO2的试验。Bur等[4]通过研究风洞与“Pathfinder”(“探路者号”)的计算数据，认为风洞条件下驻点和前体部分热流计算峰值要高28%。Armenise等[5]则对风洞条件和飞行条件下的计算化学反应模型进行了分析和验证。Paterna等[6]通过试验和计算，认为火星再入飞行器在CO2气体环境下的计算，采用催化壁条件获得到的物理参数更为合适。

鉴于风洞试验在火星再入飞行试验中的重要性，需要建立风洞条件与飞行条件之间的相关性。基于众多科研工作者的开拓性研究，本文利用了“Pathfinder”风洞试验数据[7-8]和飞行试验数据[9-10]，通过数值方法，建立了火星再入飞行器气动力和气动热的风洞参数外推方法。

1 物理模型和计算方法

1.1 物理模型

本次计算采用的是“Pathfinder”火星再入飞行器的飞行数据[11]和风洞试验数据[12]，其中风洞数据来源于“MP-1”模型的风洞试验数据[12]，飞行数据来源于“Pathfinder”的飞行数据[10]。两者前体几何相似，缩尺比例为1|∶ 52.15，如图1[11]和图2[12]所示，其中图2中1 in= 0.025 4 m。表1[12]中CASE 1和CASE 2是两种常规高超声速空气风洞试验条件及其对应的飞行状态。CASE 3是试验介质分别为空气、CO2的高焓风洞试验数据及其对应的飞行数据。在本文计算中，认为火星大气其主要成分是由体积分数97%的CO2和3%的O2组成；空气的主要成分由体积分数79%的N2和21%的O2组成；来流风洞的主要成分由体积分数为100%的CO2组成。

CASE 1中，风洞试验焓值达到H0,2-H298=(0.756±0.037 8) MJ/kg。CASE 2 中，风洞试验焓值为H0,2-H298=(0.764±0.007 64) MJ/kg。CASE 3中，介质为CO2的风洞试验焓值为H0,2-H298=(12.25±0.26) MJ/kg，介质为空气时的风洞试验焓值为H0,2-H298=(14.18±0.28) MJ/kg。 CASE 1、CASE 2和CASE 3中，风洞模型的双尺度ρ∞L与飞行器的双尺度一致。双尺度ρ∞L中的ρ∞为来流密度，L为飞行器或风洞模型头部的有效直径。表1中u∞为来流速度，T∞为来流温度，p∞为来流压力，Ma∞为来流马赫数，Re∞为来流雷诺数。“97%CO2+3%N2”代表来流介质的主要组成成分是体积分数97%的CO2和3%的N2，即真实飞行条件中的火星大气，“21%O2+79%N2”代表来流介质的主要组成成分是体积分数21%的O2和79%的N2，即空气风洞试验中的空气，“100%CO2”代表来流介质的主要组成成分是体积分数100%的CO2，即CO2风洞试验中CO2。CASE 1和CASE 2中的风洞试验条件为低焓风洞试验条件，CASE 3 中的风洞试验条件为高焓风洞试验条件。

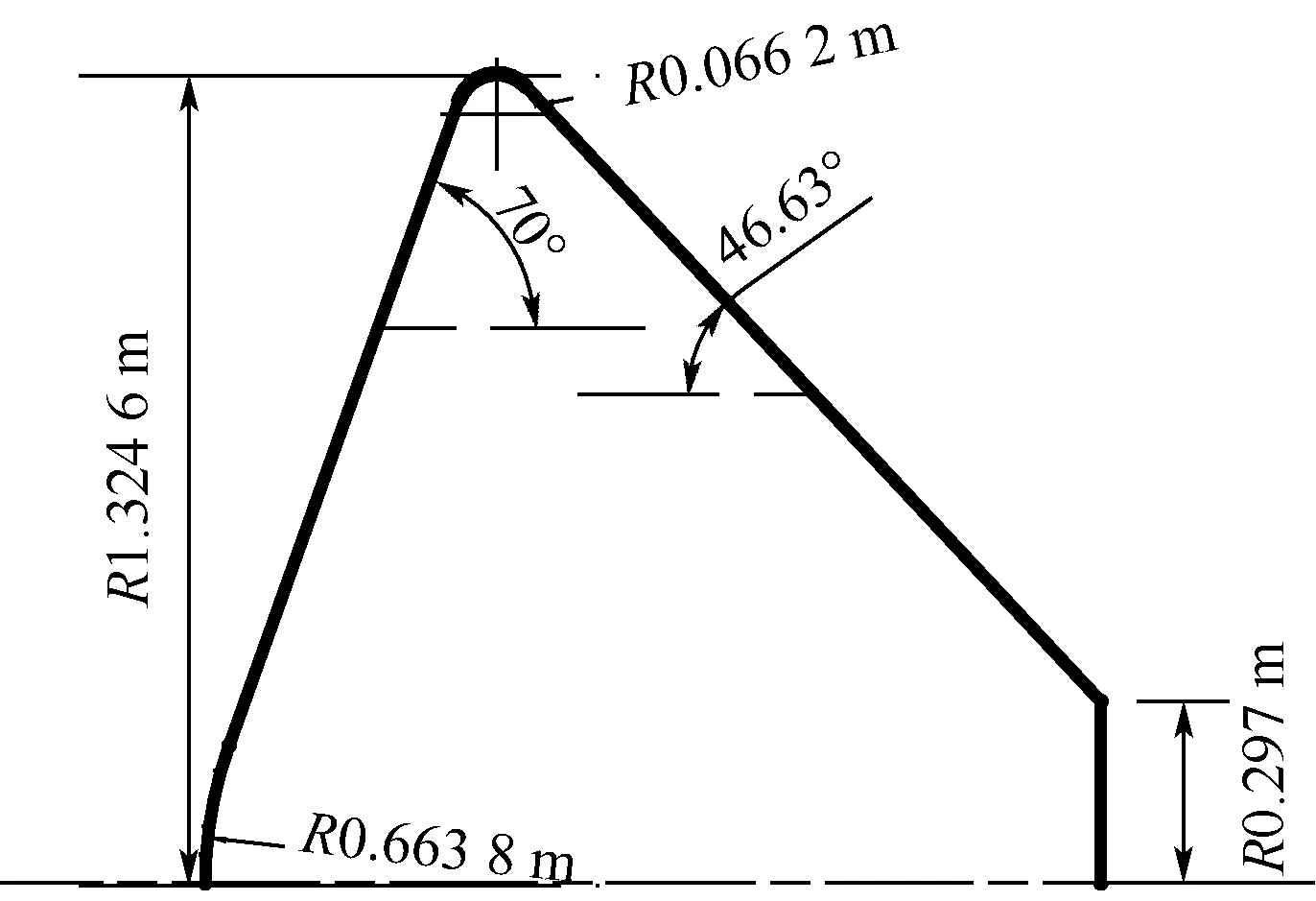
图1 “Pathfinder”计算模型[11]Fig.1 Calculation model of “Pathfinder”[11]

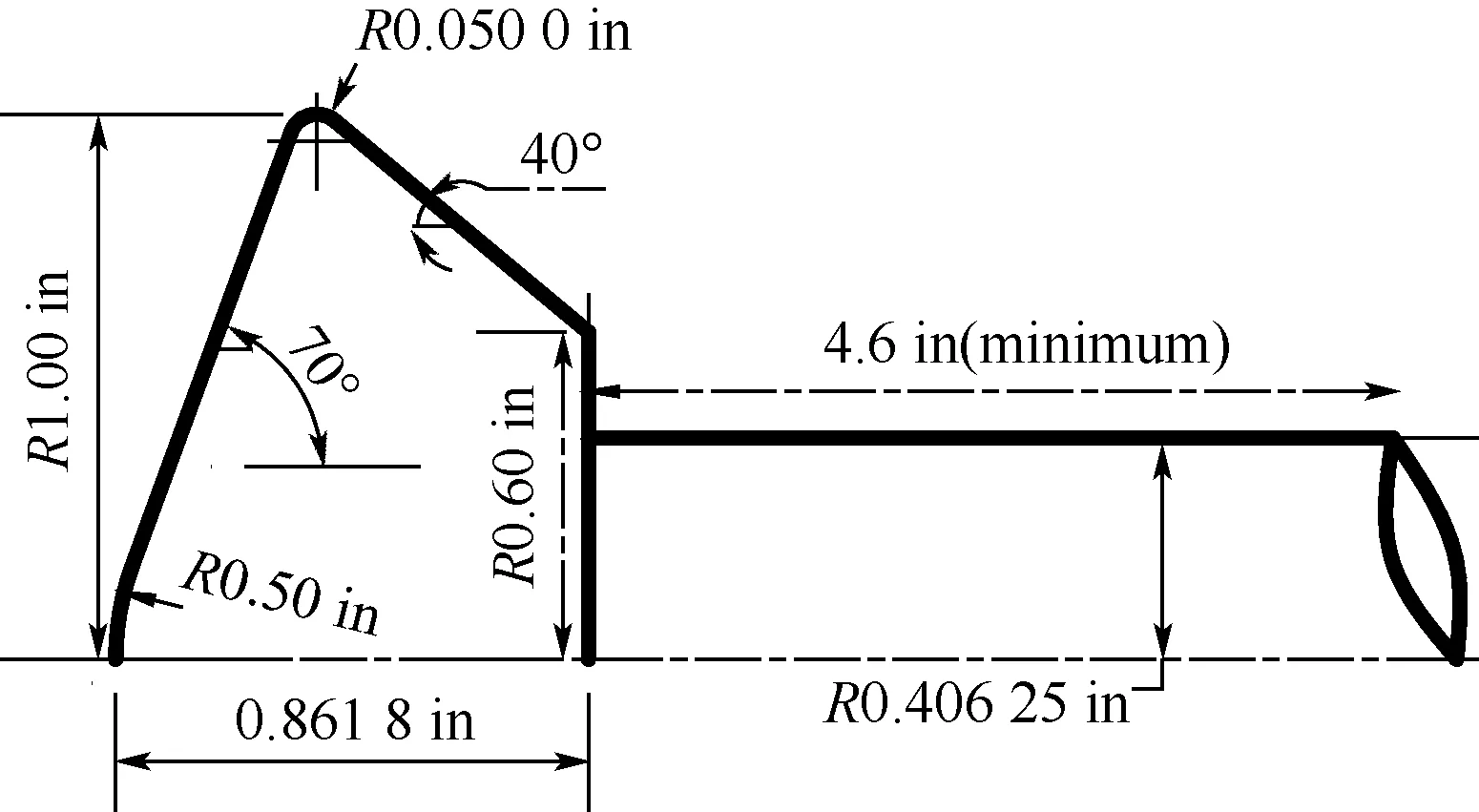
图2 “MP-1”计算模型[12]Fig.2 Calculation model of “MP-1”[12]

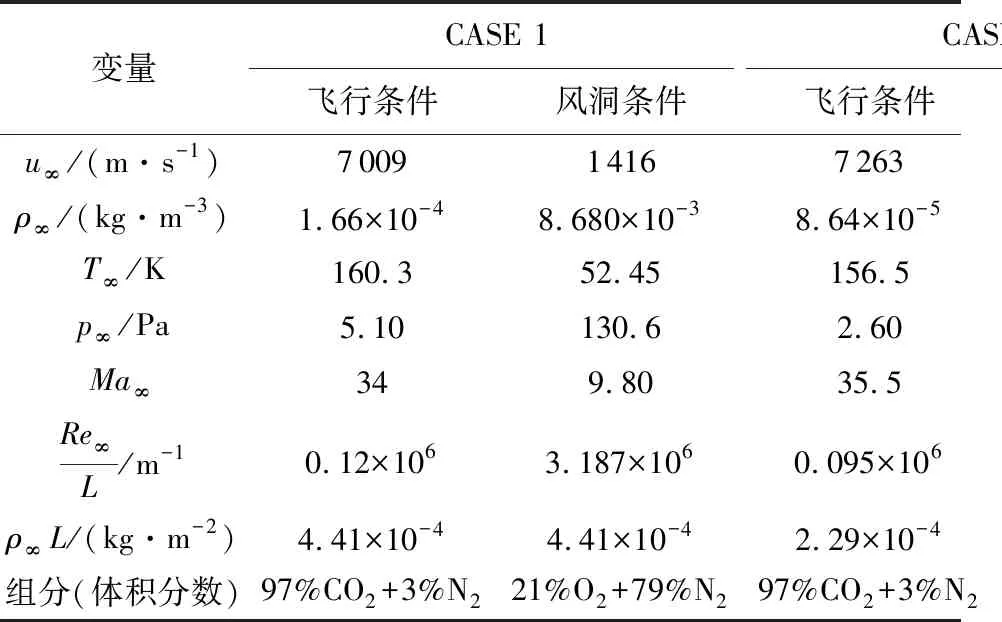
表1 计算条件[12]Table 1 Calculation conditions[12]

1.2 计算方法

求解的控制方程为采用化学反应全Navier-Stokes方程求解二维轴对称外形，并基于以下假设：流动为热力学非平衡；忽略辐射和彻体力的影响；流动质量采用双组元气体模型；温度模型采用Park双温模型[13]；壁面采用完全催化壁，壁面单原子和离子浓度为0；常温风洞条件下壁面温度设置为300 K，高焓风洞条件和飞行条件下的壁温设为2 000 K。

对于空气的化学反应模型，采用Park 5组分化学反应模型[13]，如表2所示。对于CO2的化学反应模型，则采用8组分9化学反应模型[14]，如表3所示。

采用有限体积法对控制方程进行数值求解，空间格式采用二阶TVD格式，黏性项采用二阶中心差分，时间格式采用隐式求解。

计算网格采用代数关系方法生成，为了模拟附面层，壁面网格采用了线性函数来加密。由于热流是以黏性为主导的物理量，高超声速飞行器的气动热计算对网格依赖性较高。根据文献[15]，在高超声速中，网格雷诺数小于8可以获得收敛的热流结果[15]。所以在本文计算中，所有网格雷诺数均小于8。“MP-1”与“Pathfinder”网络如图3、图4所示。

表2 5组分化学反应模型[13]Table 2 Mechanism with five species chemical reactions[13]

表3 8组分9化学反应模型[14]Table 3 Mechanism with eight species and nine chemical reactions[14]

图3 “MP-1”的网格Fig.3 Mesh of “MP-1”

图4 “Pathfinder”的网格Fig.4 Mesh of “Pathfinder”

2 计算结果

2.1 对比验证

通过与NASA Langley研究中心“Pathfinder”飞行状态计算结果[9-12]的对比，来验证本文所采用的热力学模型和计算方法能否用于飞行条件下的飞行器流场计算；采用表1中CASE 3的CO2条件开展计算，将计算结果与风洞试验结果[12]进行对比，来验证本文所采用的热力学模型和计算方法能否运用于风洞条件下的模型流场计算。

图5为采用本文方法计算得到的风洞条件下的模型表面热流与风洞试验数据[12]的对比曲线。

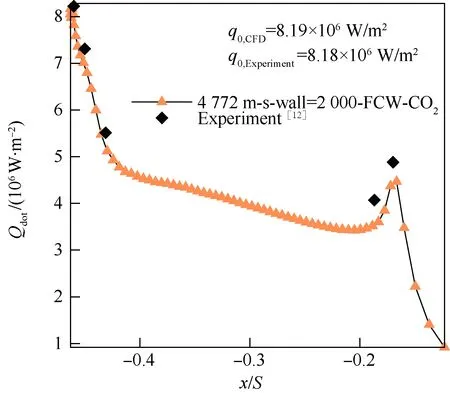
图5 气动热对比(风洞条件)Fig.5 Comparison of aerodynamics (wind tunnel condition)

图中“4 772 m-s-wall=2 000-FCW-CO2”表示来流速度为4 772 m/s、来流介质为CO2，对应表1中的CASE 3下的风洞条件中的CO2风洞条件；壁温Tw=2 000 K、壁面条件为完全催化壁(FCW)。x/S表示壁面投影到x轴的坐标，x轴为飞行器或风洞模型的几何旋转轴，坐标原点为驻点位置，下同；Qdot为壁面热流；“Experiment”表示文献[12]中的风洞条件下的试验数据(下文图中的曲线标识类似)。根据参考文献[6]，在飞行条件下的飞行器流场计算中，壁面条件采用完全催化壁。从图5可以看出，风洞条件下的热流峰值计算q0,CFD与试验q0,Experiment相差0.1%，试验点上最大的误差为8%，证明所采用的热力学模型和计算方法在风洞条件下的计算精度可以满足分析要求。

表4为采用本文的计算方法得到的飞行状态驻点热流与文献[8]中计算结果的对比。从表4可以看出，本文的计算方法在飞行状态时的计算结果与NASA Langley中心计算结果最大误差为6%，表明本文的计算方法对飞行条件下的计算精度满足分析要求。

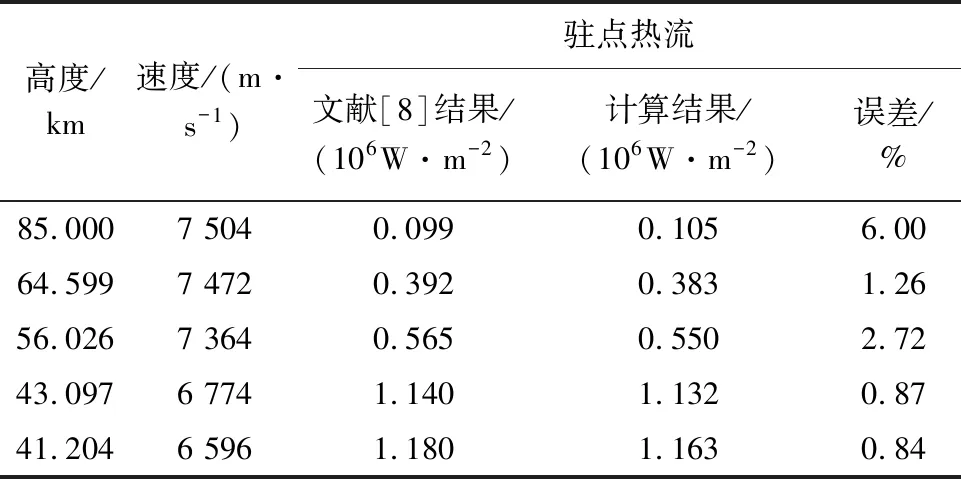
表4 对比条件和计算结果(飞行条件)Table 4 Comparison conditions and computation results(flight condition)

2.2 表面压力试验相关性

由于低焓风洞中流场温度较低，所以在“MP-1”计算中仅考虑冷壁(壁温Tw=300 K)非催化壁条件；在高焓风洞条件下，来流温度较高，为了比较冷壁和热壁(Tw=2 000 K)条件对相关性的影响，在“MP-1”计算中分别采用冷壁和热壁2 种计算条件，以便对比分析火星再入飞行器飞行状态下冷壁和热壁对相关性的影响。

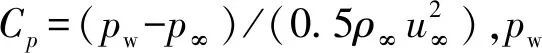
图6 风洞条件和飞行条件压力系数Fig.6 Pressure coefficient of wind tunnel and flight conditions

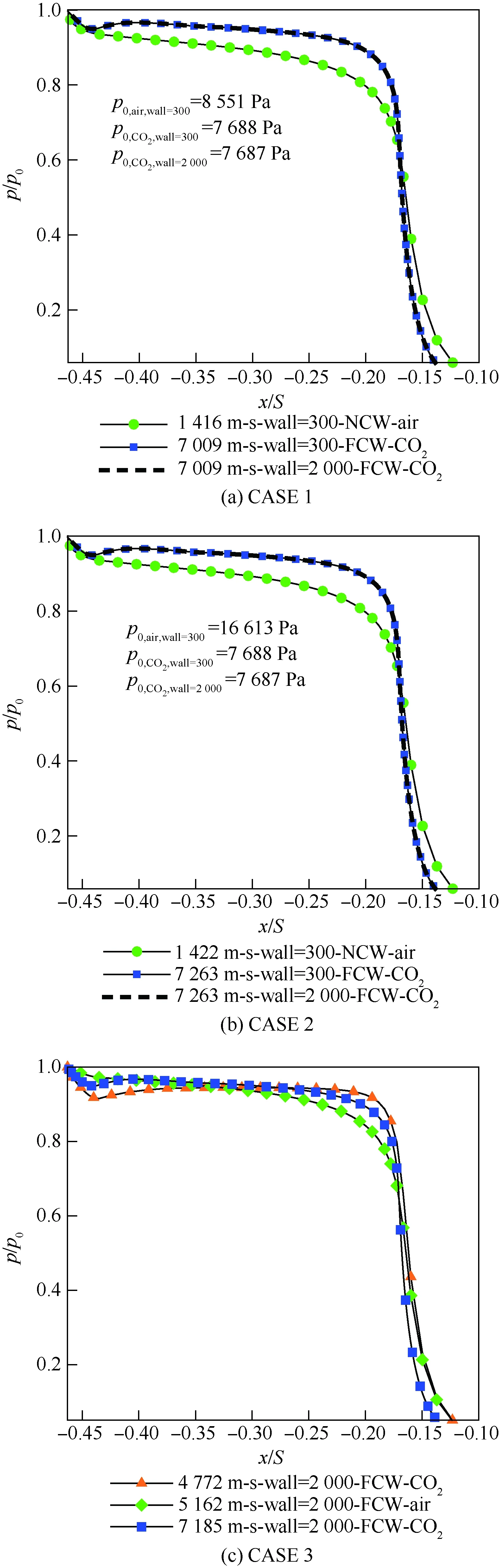
图7 风洞条件和飞行条件无量纲压力Fig.7 Dimensionless pressure of wind tunnel and flight conditions

从图6(a)、图6(b)、图7(a)和图7(b)中可以看出，对于低焓风洞试验的压力系数和无量纲压力，在驻点附近时与飞行数据相差很小；从驻点沿壁面向肩部发展，低焓风洞试验结果与飞行数据之间差距逐渐增大，最大相差11.5%。壁面温度对飞行状态下的压力系数和无量纲压力没有明显的影响。

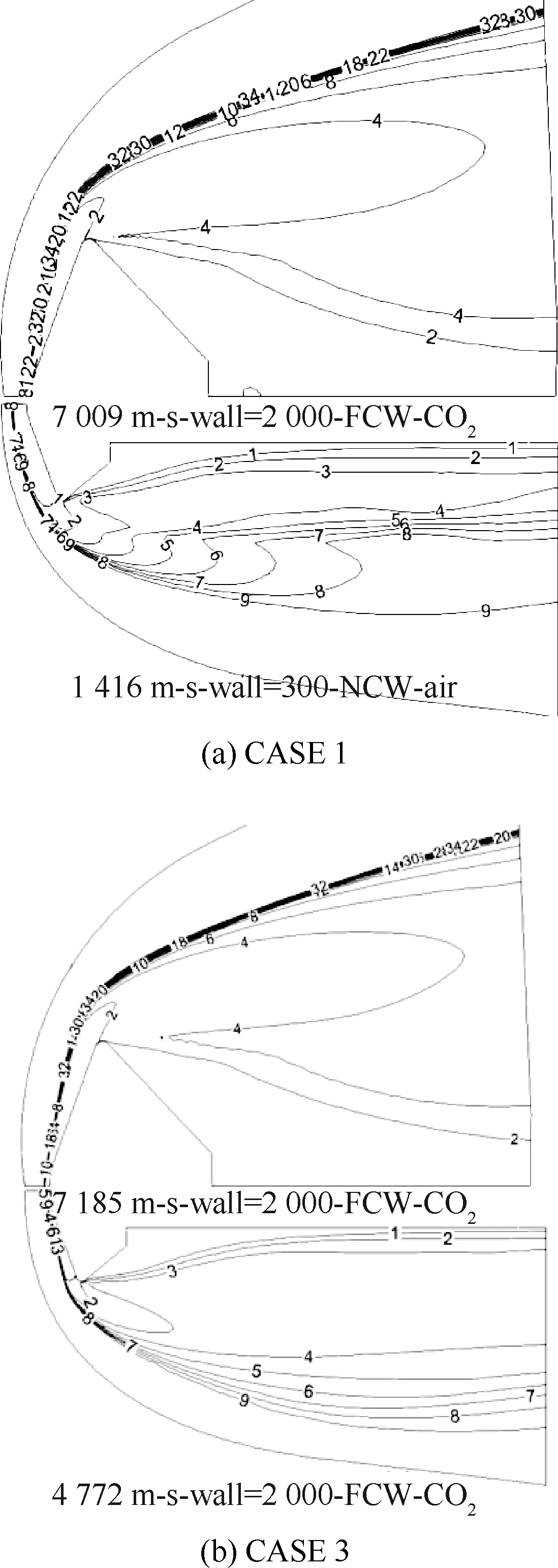
图8 风洞条件和飞行条件的马赫数对比Fig.8 Mach number comparison of wind tunnel and flight conditions

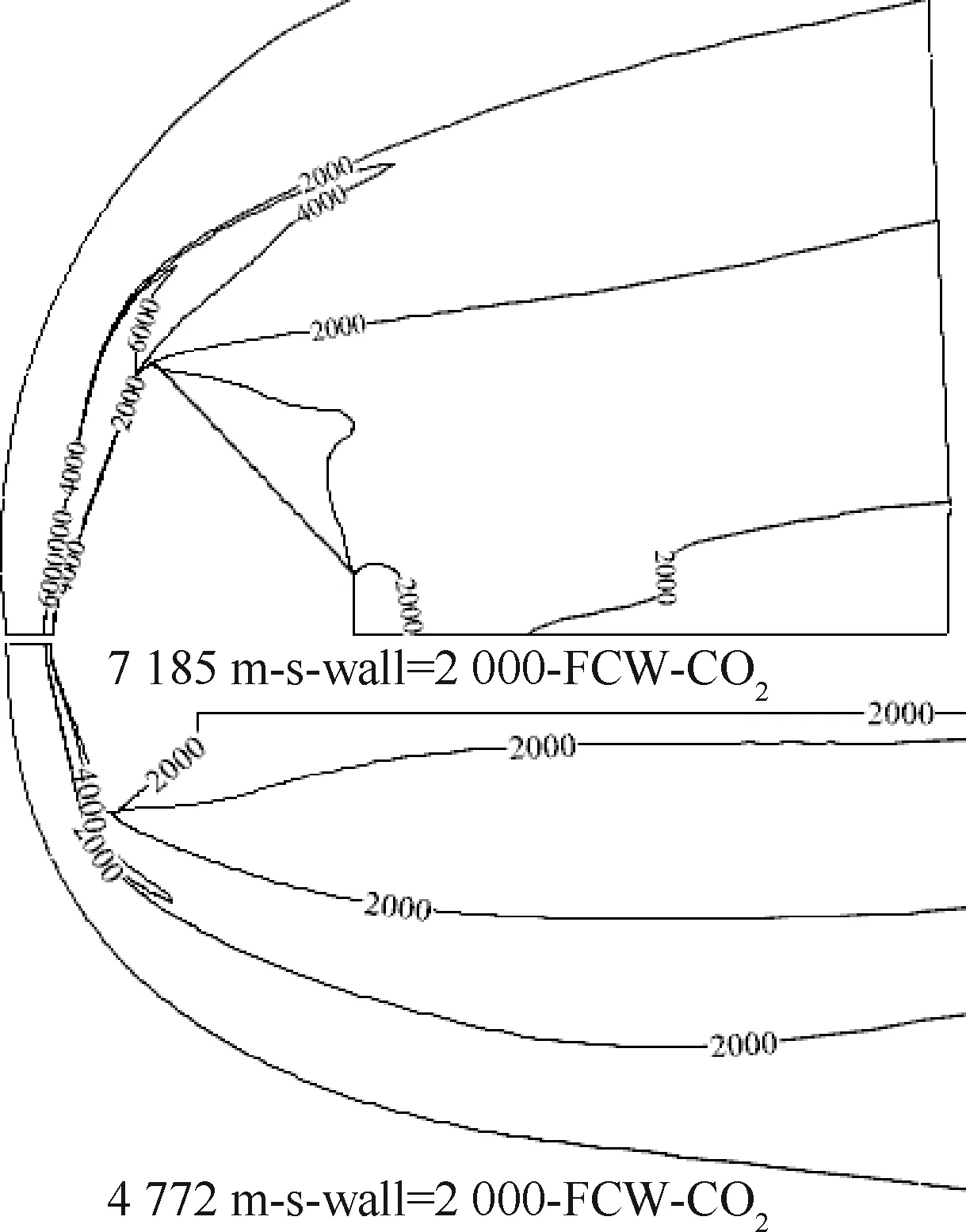
图9 风洞条件和飞行条件的温度对比Fig.9 Temperature comparison of wind tunnel and flight

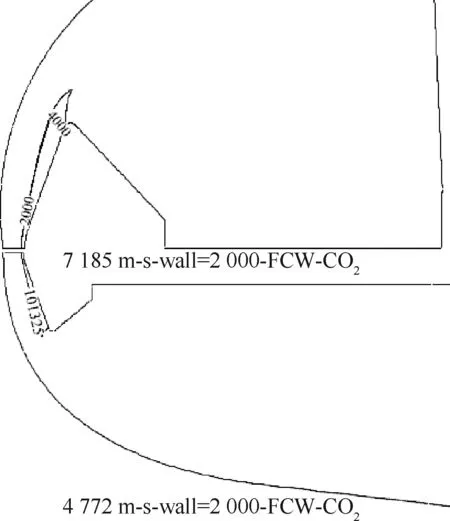
图10 风洞条件和飞行条件的压力对比Fig.10 Pressure comparison of wind tunnel and flight

从图6(c)和图7(c)可以发现，对于高焓风洞试验压力系数和无量纲压力，以及高焓CO2风洞试验压力系数与无量纲压力，除了模型驻点附近区域以外，其他地方与飞行状态下的压力系数和无量纲压力有明显的差距；对于高焓空气风洞试验的压力系数和无量纲压力，从驻点沿壁面向肩部发展，与飞行条件下的压力系数和无量纲压力几乎吻合。高焓空气风洞试验无量纲压力和压力系数，比常温空气风洞试验的无量纲压力和压力系数更接近于飞行条件下的无量纲压力与压力系数。

在低焓风洞条件与真实飞行之间出现以上情况的主要原因是马赫数影响。由于常温下空气的比热比与火星大气比热比接近，根据马赫数无关原理，对于高超声速飞行，当马赫数较高时，压力系数基本上与马赫数无关，仅与流动介质的比热比相关。根据表1可以发现，不管CASE 1和CASE 2 的风洞条件还是飞行条件，来流马赫数都较高，因此低焓风洞试验模型的驻点处的压力系数与飞行条件下的驻点压力系数接近。根据图8(a)可以知道，从模型驻点处沿着壁面向肩部发展，激波层内的马赫数逐渐降低，模型肩部附近马赫数较小。根据牛顿修正公式[16]，当马赫数逐渐减小时，压力系数等参数逐渐减小，而且当比热比越大，压力系数的变化幅度也越大。所以当压力系数和无量纲压力逐渐从模型驻点沿壁面向肩部发展而逐渐减小，且空气介质中的减小幅度大于CO2介质中的减小幅度。

分析高焓风洞试验和真实飞行的流场，根据图8(b)可知，两者来流马赫数都比较高，所以引起压力系数和无量纲压力变化差异的原因主要在于温度。标准大气压下，CO2在5 000 K时完全分解，且CO2分解的温度域很小。O2在2 000 K左右开始分解，4 000 K左右时完全分解，N2在3 000 K左右开始分解，9 000 K几乎完全分解。从图9和图10可知，在高焓CO2风洞试验中，模型驻点到肩部区域的激波层内温度不超过4 000 K，模型头部驻点附近激波层内的压力略大于101 325 Pa。根据高超声速理论，除了振动激励现象不受压力影响以外，如果压力上升，其他起始温度将会对应上升[16]。即压力大于101 325 Pa时，气体的分解起始温度比101 325 Pa下的分解起始温度要高；当压力小于101 325 Pa时，气体的分解起始温度温度比101 325 Pa下的分解起始温度要低。所以在CASE 3中的高焓CO2风洞试验中，CO2并未发生分解，整个流场均为CO2气体。在CASE 3中的高焓空气风洞试验中，由于其来流条件与高焓CO2风洞试验来流条件接近，激波层内的压力与高焓CO2风洞试验相差不大，略大于101 325 Pa；空气主要成分是O2和N2，且O2和N2均发生了分解反应，O2甚至可能已经完全分解，因此从模型驻点沿壁面向肩部发展的流场区域内，气体的性质主要以单原子气体为主。

分析图9和图10可知，在飞行条件下，飞行器驻点附近到肩部区域激波层内温度明显高于6 000 K，而激波层内压力小于101 325 Pa，因此飞行条件下的CO2起始分解温度小于5 000 K。由于火星大气主要成分以CO2为主，在飞行条件下的流场中CO2会发生分解反应。此时，从模型驻点沿壁面向肩部发展的流场区域内的气体性质主要以单原子气体为主。

因此，在保证双尺度ρ∞L，在零攻角情况下的驻点处，均有

Cp,windtunnel=Cp,flight

(1)

(2)

式中：下标windtunnel表示风洞条件下的物理量；flight表示飞行条件下对应飞行器的物理量;“0”表示驻点处的物理量。

2.3 表面热流试验相关性

图11是高焓风洞试验模型壁面热流分布比较。图11(a)是两种不同介质情况下在不同壁温时的热流分布，同时给出了驻点热流的计算结果和试验结果。可以看出，壁面条件采用高温催化条件(Tw=2 000 K)时，计算结果与试验结果峰值接近，最大相差0.12%。说明本文热流计算方法合理。但是当采用冷壁条件(Tw=300 K)时，计算结果与试验结果相差较大，其中，高焓CO2风洞试验中，风洞模型的驻点热流与试验值相差18.7%；在高焓空气风洞中，风洞模型的驻点热流与试验值相差7.4%。结合图5，可以发现在高焓CO2风洞试验中，冷壁条件下风洞模型的热流值与试验点的热流之间的最大误差为25%，最大误差的几何位置在肩部；热壁条件下风洞模型的热流值与试验点的热流之间的最大误差为8%。在表1中，高焓CO2风洞和高焓空气风洞中来流的温度均比较高，模型壁面为高温壁面。所以采用热壁条件，得到的计算结果，比采用冷壁条件得到的计算结果，更接近于试验值。所以，在数值计算过程中，应尽量模拟壁温条件。

根据图11(a)可知，在高焓空气、高焓CO2风洞试验中，风洞模型与飞行条件下对应飞行器的双尺度一致时，以空气为介质的风洞试验热流数据明显大于以CO2为介质风洞试验结果。图11(b)是飞行条件下壁温不同时得到的热流分布，可以看出，冷壁条件下的热流分布变化趋势比较陡峭，热壁条件下热流分布相对平缓；在驻点附近，冷壁条件下的热流明显高于热壁条件。图11(c)是飞行条件与风洞条件下的无量纲热流q/q0对比数据，可以看出，无量纲化之后，以空气和CO2为介质的风洞试验的热流分布与飞行状态下的热流分布仍然不匹配。

图12为高焓风洞与飞行条件Stanton数的分布。与飞行条件相比，高焓风洞条件下的Stanton数分布明显高于飞行条件下飞行器的Stanton数分布。高焓CO2风洞试验在驻点附近区域的Stanton数，与飞行条件下的Stanton数吻合；从驻点沿壁面向后，两者之间的差距逐渐增大，其中肩部区域附近最大相差27.3%。

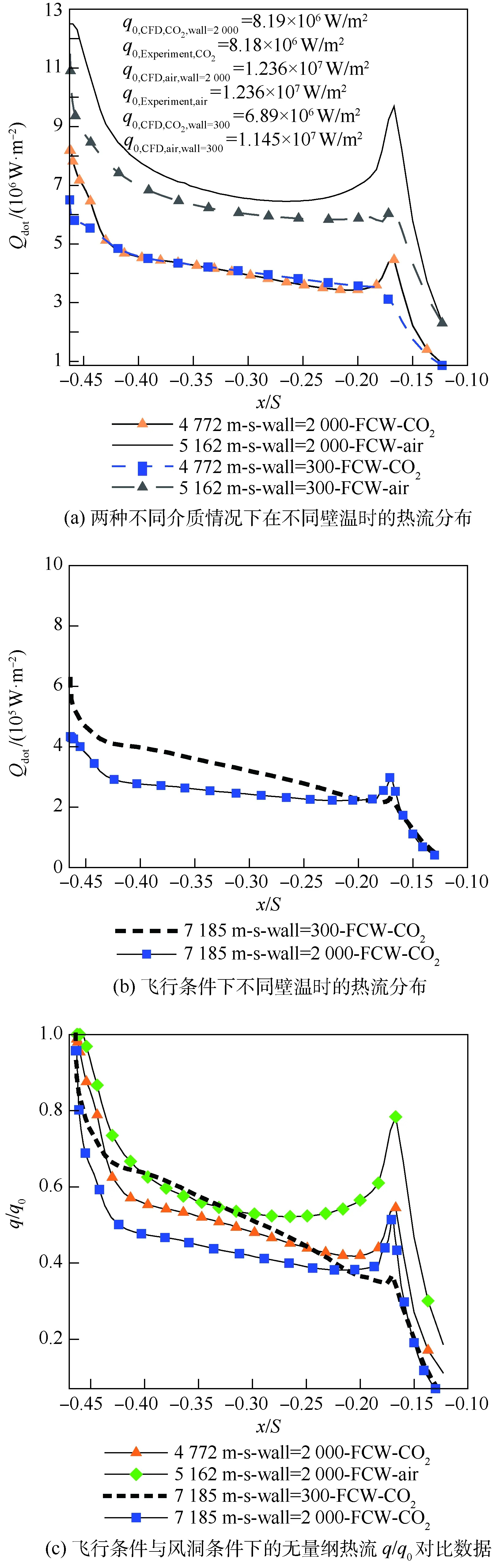
图11 壁面热流分布Fig.11 Distribution of wall surface heat flow

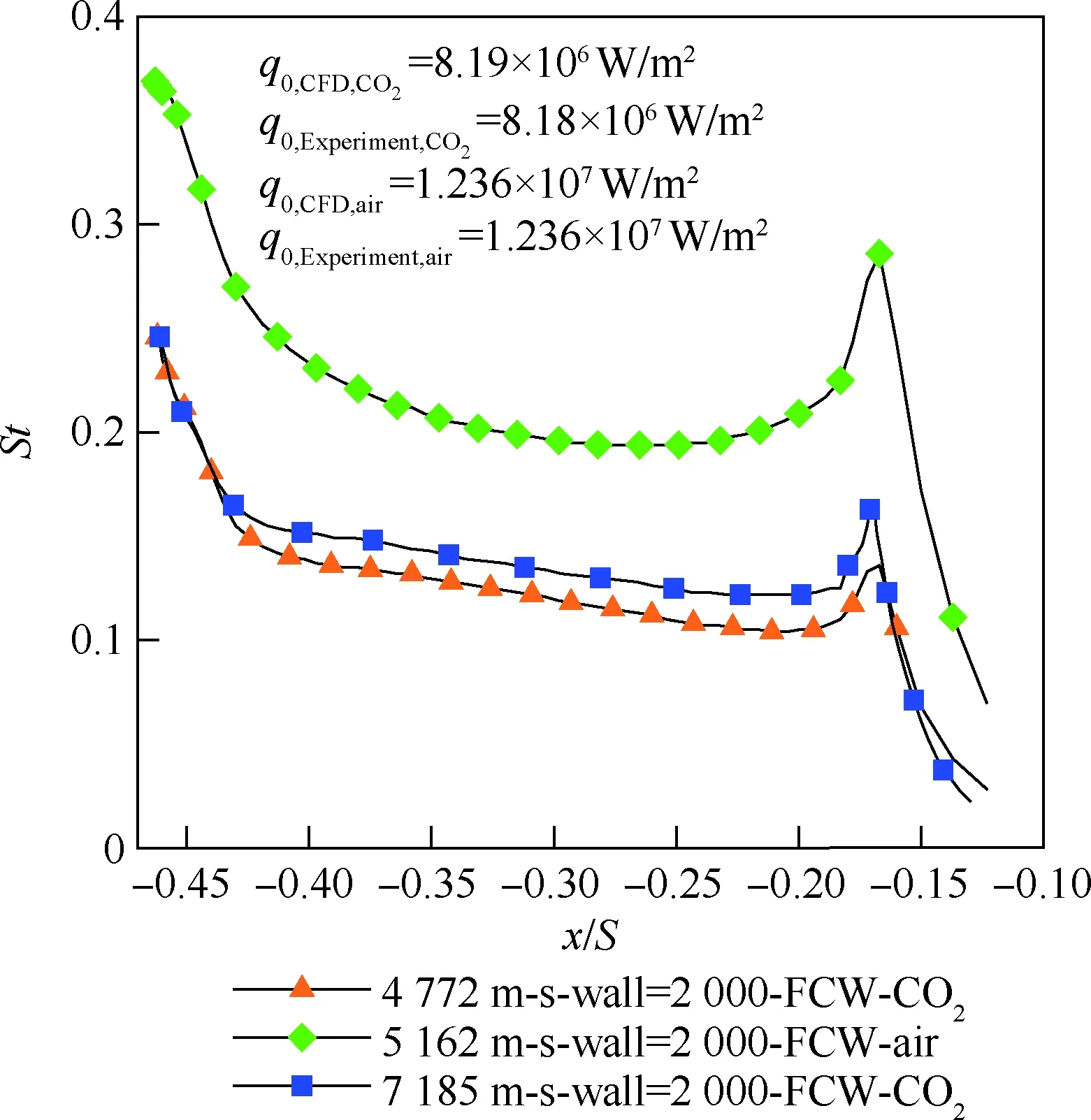
图12 壁面Stanton数的分布Fig.12 Distribution of wall Stanton number

根据上述分析可知：在数值过程中，应尽量模拟壁温条件；高焓空气、高焓CO2风洞试验的热流和无量纲热流数据，都不宜直接作为将风洞条件外推至飞行条件的外推参数。在风洞中，不能直接将高焓空气风洞试验的Stanton数作为外推参数外推到飞行条件中；在高焓CO2风洞条件下，可以在风洞模型驻点附近区域内，将风洞试验的Stanton数作为风洞试验模型与飞行试验下飞行器的相关性条件，且有：

St0,windtunnel≈St0,flight

(3)