水合物浆液在U形弯管中的流动特性
2019-04-29何骋远周诗岽
张 艺,李 聪,何骋远,李 乐,周诗岽
(1. 常州大学 石油工程学院 油气储运技术省重点实验室,江苏 常州 213016;2. 江苏城乡建设职业学院 公用事业学院,江苏 常州 213147)
天然气水合物是水和天然气分子在低温高压条件下形成的一类非化学计量型的笼形络合物[1],水合物颗粒极易在油气管道运输时生成,且在流动过程中会发生沉积,给管道安全运行带来巨大隐患。因此,研究水合物在管道内的流动特性,可为预防水合物堵管提供基础理论。水合物浆液的流动参数与颗粒直径、颗粒体积分数、流动速度等均有一定关系[2]。但目前应用实验方法对水合物浆液流动进行分析较难实现,因而应用数值模拟[3]的方法成为实验方法的有效替代手段[4]。Balakin 等[5-6]研究了湍流条件下R11水合物浆液的流动特性,实验结果表明浆液的流动特性几乎不会被低浓度的水合物颗粒所影响。Wang等[7-9]用Fluent软件模拟了水平管道中冰浆的流动,发现了压降、颗粒粒径、流速等参数在管道流动过程中相互之间的关系。赵鹏飞等[10]通过软件分析了水平管路中浆液的流动特性,研究了固相颗粒粒径、颗粒黏度和最大的内相堆积率等物性参数对浆液流动的影响。Camargo粒径模型[11]比 Mulhe粒径模型[12]更符合实际流动工况,与实验数据吻合。Balakin等[13]通过数值模拟和实验相结合的方法,还可准确预测管内沉积情况。上述模拟均未考虑水合物颗粒浓度的变化及弯管对流速和压力的影响。
本工作以实验室水合物高压环路设备为基准,建立1∶1的U形管物理模型对直管和弯管进行对比分析,利用Fluent 15.0软件对模型进行耦合求解,进而模拟流速、浓度及管型对管内水合物流动特性的影响。
1 数值模拟
1.1 几何模型的建立
图1为U形管的物理模型及网格划分。
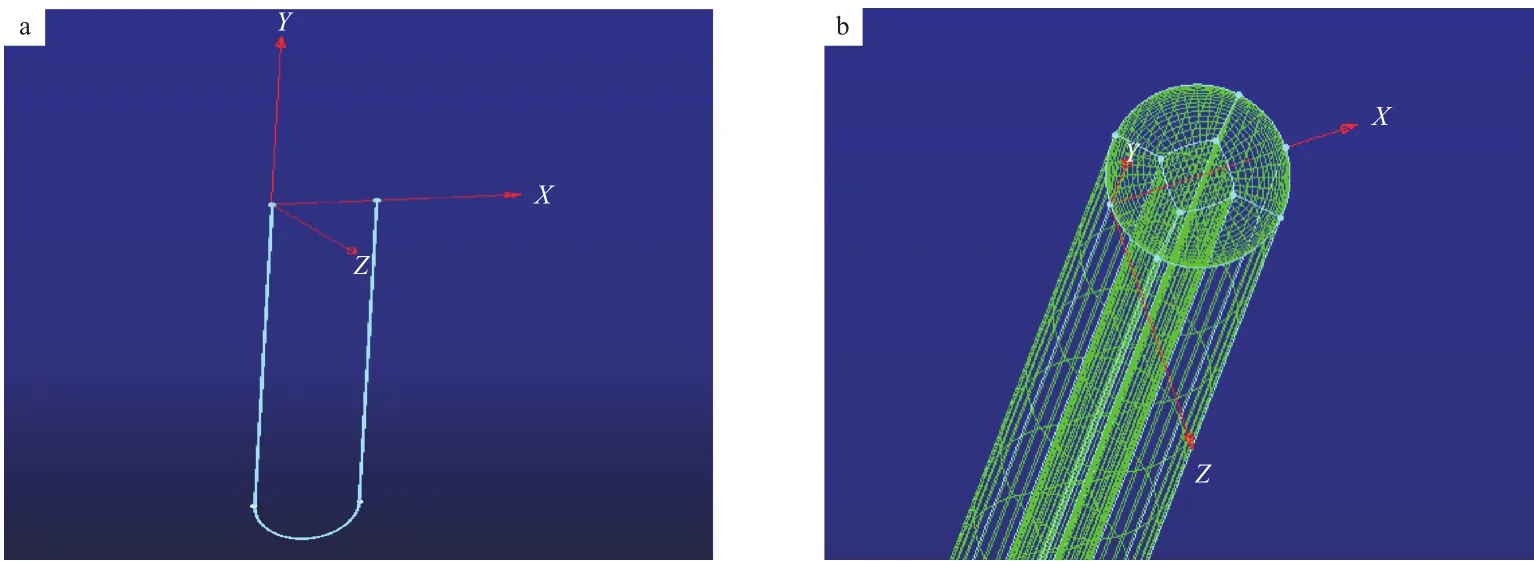
图1 U形管物理模型(a)及网格划分(b)Fig.1 Physical model(a) and grid division(b) of U-tube.
由图1可知,物理模型是规则的U形管,模型由两段相同的直管(长度为5.5 m,内径为0.254 m)和一段半圆形的弯管(半径为6.3 m)构成。网格采用多块对接网格,为了准确地计算近壁面处的流动情况,从而提高模拟结果的精确性,对管道的出入口近壁面处采用加密网格,再进行网格无关性检验,确定网格数为1 200 000。
1.2 数值模型
为使模拟更加准确,在模拟计算过程中应用以下假设:水合物浆液在流动体系中达到平衡,流动为等温过程且不计相间质量传递,即在流动过程中无水合物分解、生成、聚积和破碎,浆液只由水合物颗粒相和水相组成,忽略管壁对水合物颗粒的黏附作用。在上述条件下,为保证管内流动过程中水合物颗粒为连续介质,本工作选用欧拉-欧拉双流体模型。
采用Fluent 15.0软件进行求解计算。模拟入口条件设置为速度入口,根据国内外现有研究成果[14-15],在入口处定义初始浓度分别为37.7%,27.5%,25.4%,20.7%,研究粒径选取248,355,450 μm;出口条件设置为自由流出,压力-速度耦合采用SIMPLE模型,壁面采用无滑移边界条件[16],因为在弯管处可能会出现二次流现象,所以湍流模型采用RNG k-ε湍流方程[17],当非稳态数值计算各因子残差收敛到10-5时,认为计算结束。所有的物理模型以及所有的流动过程都是以质量守恒定律为基础。管输水合物浆液流动体系的动量方程符合牛顿第二定律的条件。
1.3 相间耦合
水合物浆液流动属于气-液-固多相流动,不同于单相流体流动。在模拟过程中,假设气体已消耗完成,即混合流动是液固两相流。当固体颗粒载荷较高时,要考虑相间耦合及曳力作用,本工作采用模型为Wen-Yu曳力模型[18]。
1.4 有效性分析
管道浆液输送时压力梯度变化是衡量管道运输的重要运行参数,根据本课题组高压可视水合物浆液实验环道的实验结果与模拟结果进行对比[19-20],发现模拟压降与实际压降的相对误差均在20%以内,与王继红等[8,21-22]国内外研究报道结果相一致,说明通过模拟的方法进行管道水合物流动分析具有可行性。
2 结果与讨论
2.1 流速分布
图2为水合物颗粒粒径及颗粒浓度对直管和弯管处截面Z方向轴线上的流速分布的影响。由图2可知,随着水合物颗粒粒径或颗粒浓度的增大,水合物颗粒流速也会小幅度的增大。由图2a,c可知,在直管横截面处流速的分布表现为下抛物线状,在管道中轴位置处流速最大;且流速在管道中分布不均匀,由管道中心向管壁处逐渐降低,这与Lahiri等[23]模拟结果相符;管壁处速降低的幅度较大,这是由于近壁面处流速低,对水合物携带能力差,所以水合物颗粒流动速度分布呈开口向下的抛物线;且呈现出很好的对称性。由图2b,d可知,由于离心力和阻力的影响,在弯管横截面处浆液流速呈大M形分布,以管道中轴位置处为分界点,上下区域呈对称分布,这与王晓娅[14]通过模拟水合物浆液在弯管处流速分布所得结果一致。
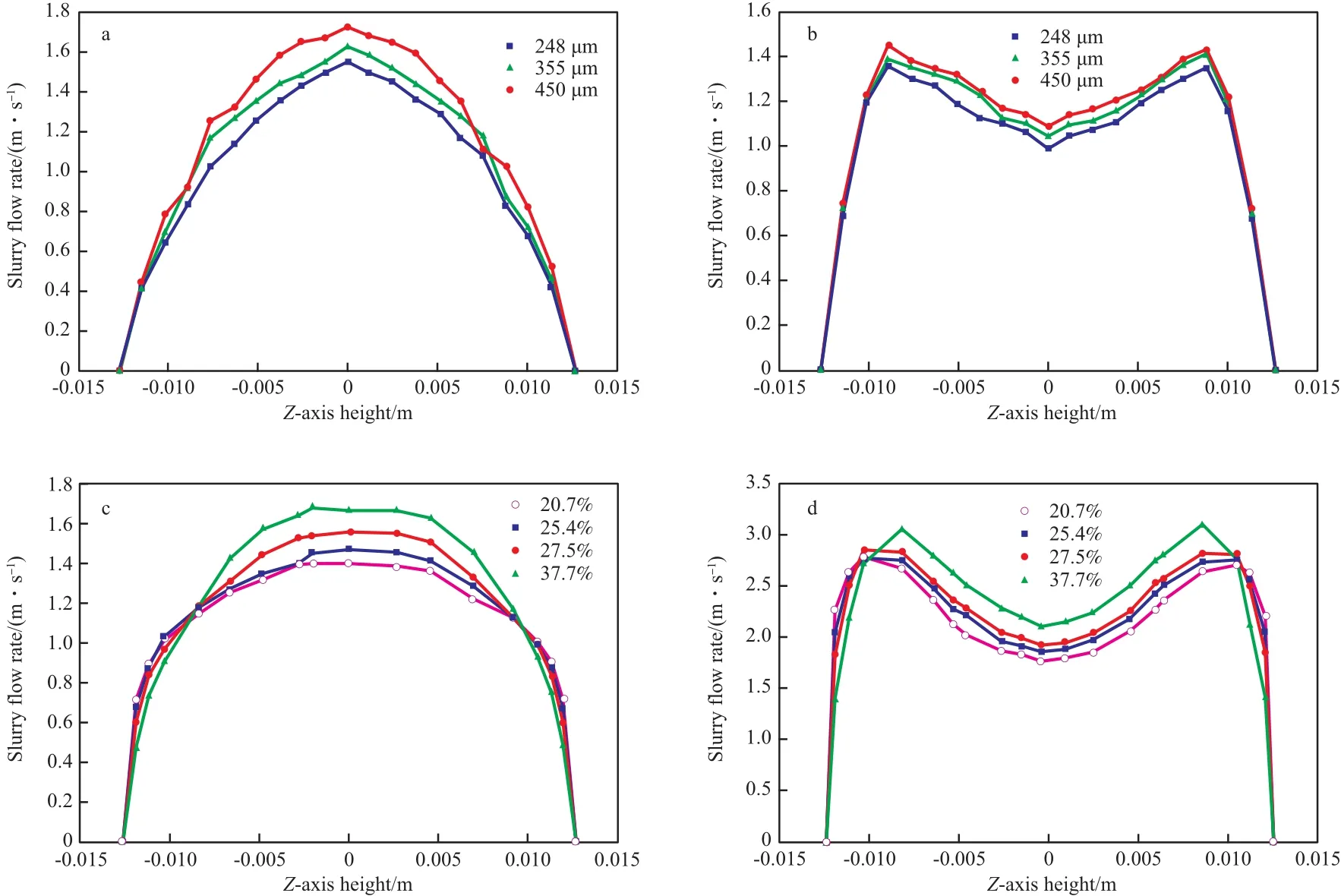
图2 水合物颗粒粒径及颗粒浓度对直管(a,c)和弯管(b,d)处截面Z方向轴线上的流速分布的影响Fig.2 Effects of hydrate particle diameter and particle concentration on velocity distribution of Z-axis of section at straight(a, c) and bend(b, d) pipe.
图3为弯管入口和出口横截面处流速分布。由图3a可知,弯管入口处流速分布较均匀,以管轴线为中心,上下呈半圆形对称分布。由图3b可知,弯管出口部分的速度呈凹凸的椭圆形对称分布,这是因为离心力的作用以及流体撞击壁面受到阻力的影响,以管段中轴处向管壁处流速由大变小;最大速度偏向弯管截面内凹侧的位置,且弯管截面部分外侧速度急速下降。由于流体的动量动能不断发生交换,导致浆液流速在管道内部分布不均匀,且弯管处流速大于直管处流速。这种弯管二次流现象,主要由于流体在管道中流动时,弯管处会受到离心作用,流速越大离心作用也就越明显。受离心力作用的影响,水合物浆液首先会向弯管部分外凸侧流动,然后由于内侧出现真空,受压力作用再流回内侧。此流动现象与四氢呋喃在弯管处流动现象相似[14]。
2.2 颗粒浓度分布
图4为水合物颗粒粒径对管道中水合物颗粒浓度分布的影响。由图4a可知,在直管截面Z方向上颗粒浓度分布可分为3部分:高浓度区域(管道的上部)、在管的中心部分几乎与入口浓度一致的均匀分布的区域和在下管壁附近具有最低浓度的区域[24];且随着固相颗粒粒径的增大,管道中水合物颗粒浓度变化的幅度也增加。因为中间流体的流速比其他区域大,剪切作用较为明显,影响颗粒的分布,使颗粒具有离散分布的趋势,且由于浓度的增加,导致流体的湍流特性增大,使液相与颗粒相混合更加充分,从而使管道中部区域处于均相悬浮流的状态[25]。在近壁面处,浆液流速较低,颗粒具有聚集的趋势,表现出不均匀流动状态。同时因为管道中的水合物密度小于水的密度,会出现水合物颗粒更多地聚集在管道上部的现象。由图4b可知,在弯管截面Z方向上管道中部区域处水合物颗粒浓度分布整体较为均匀,在靠近管壁处颗粒浓度变化较大,管道上、下部区域,颗粒浓度均减小。随着颗粒粒径的增大,颗粒浓度也随之增大;颗粒粒径为450 μm时,颗粒浓度波动的范围变化较大,中部区域颗粒浓度范围为27.5%~28.3%。弯管处颗粒浓度分布呈中部高于管壁处的趋势,出现该现象主要是因为水合物浆液在流经弯管时,不仅受到惯性力和曳力作用,还受到离心力的作用,且离心力最大,起主导作用;与此同时由于水合物的密度小于水的密度,即水合物颗粒受到的离心力小于液相受到的离心力;因此出现管道中部颗粒浓度大于上下管壁处颗粒浓度的现象。
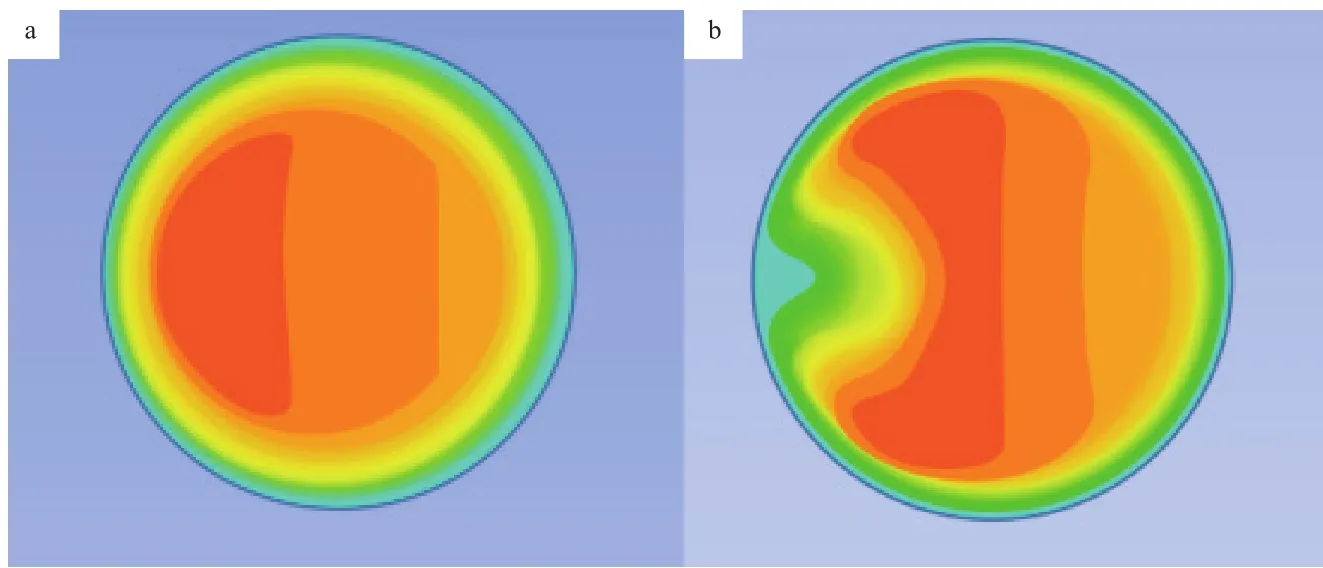
图3 弯管入口(a)和出口(b)横截面处流速分布Fig.3 Flow rate distribution at the cross section of the bend inlet(a) and outlet(b).
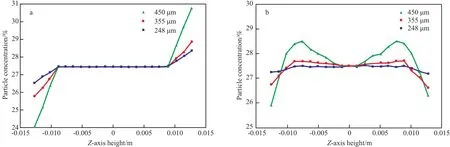
图4 直管(a)和弯管(b)截面Z方向轴线上水合物颗粒浓度分布Fig.4 Hydrate particle concentration distribution on the Z-axis of straight(a) and bend(b) pipe section.
2.3 管道沿线浆液流场分布规律
图5为颗粒粒径和浆液流速对管轴线处浆液体积分数的影响。由图5a可知,浆液流经管道入口处时,水合物浆液体积分数先降低后升高,然后趋于稳定状态;在流经弯管处,浆液体积分数急速增大,最后减小并趋于稳定。由图5b可知,在流体流动稳定状态下,流速为1,2,3 m/s对应的浆液体积分数均在27.6%附近。整个流动过程中,粒径对浆液体积分数在管道中的分布影响很小,弯管对浆液体积分数影响相对较大。而浆液流速对水合物浆液体积分数的分布影响很小,可忽略不计。流速越高,流体对水合物颗粒的携带和分散能力就越强,水合物颗粒分布越均匀。这与宋光春等[21]的模拟结果一致。
2.4 弯曲段压力分布
图6为流体流经弯管处沿X轴方向以及Z轴方向的压力分布。
由图6a可知,流体流经弯管处,X轴方向上压力分布不均,从左(管道内凹侧)到右(管道外凸侧)压力逐渐增大,在管壁外凸侧0.012 7 m附近,压力达到最大。由图6b可知,在Z轴方向上,压力呈倒U形分布,在管道中部区域,压力存在波动,但波动范围不大,在管壁处压力降低。上述现象是因为流体流经弯管处,受离心作用的影响产生弯管二次流[26],流体流动状态发生改变;流体会向外凸侧集中,导致内凹侧流体流失,形成中空区域,为保持稳定流动,外凸侧的流体会向内凹侧流动填补中空区域,因此从左(管道内凹侧)到右(管道外凸侧)压力逐渐增大。且由于流体在弯管处受到离心力的作用,弯管处压力由内侧到外侧逐渐增大。这与纪宏超等[27]用Fluent模拟的弯管处流动特性一致。

图5 颗粒粒径(a)及浆液流速(b)对管轴线处颗粒浓度分布的影响Fig.5 Influence of particle diameter(a) and slurry flow rate(b) on particle concentration at pipe axis.a Slurry flow rate 3 m/s;b Particle dimeter 248 μm

图6 弯管处沿X轴线方向上(a)及Z轴线方向上(b)压力分布Fig.6 Pressure distribution along the X axis(a) and Z axis(b) at the bend pipe.
3 结论
1)在直管横截面处流速呈抛物线分布,流速在管道中间区域最大,靠近管壁流速逐渐减小。在弯管横截面处流速呈M形分布,流速从管道中心到管壁处,先增大后减小。相对于水合物颗粒浓度、颗粒粒径对流速分布的影响,弯管对浆液流速分布影响更大。
2)水合物的密度小于水的密度且受颗粒自身重力等因素的影响,在管输过程中,受流动剪切的影响,颗粒分布不均匀,靠近上管壁区域颗粒浓度较高,靠近下管壁区域颗粒浓度较低,管中部区域颗粒浓度均衡。
3)浆液流经弯管处时,产生二次流动现象,且由于离心力的影响,在管道X轴线处外凸侧的压力大于内凹侧的压力值;在管截面Z轴处压力呈倒U形分布。
