气相入侵方式对多孔介质蒸发特性的影响

2019-04-29杨磊，吴睿

石油化工 2019年4期

杨磊，吴睿

（上海交通大学机械与动力工程学院，上海 200240）

多孔介质蒸发是构成众多自然现象和实际生产的基本过程，在能源、化工、环境、农业等领域有着重要的应用［1-4］。为了研究多孔介质蒸发过程特性，目前主要有两种基于不同尺度的分析方法，即连续性方法与非连续性方法。两种方法分别从宏观尺度（REV尺度）与孔隙尺度对蒸发现象进行研究。连续性方法将多孔介质视为一种假想的连续性介质，通过对孔隙尺度的输运方程进行体积平均，获得REV尺度上的连续性方程［5-6］。REV尺度相较于整个多孔介质的尺寸而言足够小，相较于孔隙尺寸而言足够大［7］。连续性方法通过体积平均的方式避免了多样的孔隙结构使问题复杂化的现象，但同时也忽视了孔隙尺度上的细节特征，无法将孔隙尺度上发生的现象与宏观的蒸发过程联系起来。非连续性方法则采用多孔网络模型模拟真实多孔介质内部的复杂孔隙结构［8-11］，通过求解各个孔隙中气液两相的质量、能量、动量守恒方程，从孔隙尺度上研究多孔介质的蒸发特性。

连续性方法与非连续性方法均已广泛应用于多孔介质蒸发特性的研究，但用非连续性方法评估连续性方法的研究甚少。Moghaddam等［12］应用多孔网络模型的方法获得了连续性模型中的扩散系数与局部液相饱和度间的关系，但该模型并未考虑Wu等［13-15］在多孔介质气液两相流动实验中发现的毛细阀效应。该效应是指气液界面移动到突然扩张的几何截面时，由于接触角突然增加，导致三相接触线停止向前移动。只有当入侵相与被入侵相间的压差达到某个临界值时，三相接触线才能继续向前移动。由于毛细阀效应的存在，在多孔介质的两相传输过程中，可以观测到两种气相入侵孔体内液相的方式：一种为突破入侵，另一种为聚合入侵［13-14］。在毛细数（黏性力与表面张力之比）较低时，当气相入侵孔体内液相的方式为突破入侵占主导时，多孔介质内部的两相流动是一个毛细指进的过程，而当聚合入侵占主导时，则是一个稳定的过程。气相入侵孔体内液相的方式不仅取决于孔隙的结构，也同样取决于孔隙的润湿性。

本工作采用考虑毛细阀效应的多孔网络模型，首先从孔隙尺度上研究了不同孔隙入侵方式占主导时单一润湿多孔介质的蒸发特性，而后探索了连续性模型中湿分扩散系数与局部液相饱和度的关系，并确立了表层控制体液相饱和度与表面蒸汽浓度的关系。

1 多孔网络模型

多孔网络模型由一系列规则的孔体与连接孔体的喉道组成，每个孔体为大小不一的正方体，喉道横截面为正方形。孔体边长与喉道的宽度均匀分布在一定范围内。多孔网络模型由多个正方体单元组成，任意两个相邻单元的中心距离均相同。多孔网络模型的二维视图见图1。

图1 多孔网络模型的二维视图Fig.1 Two-dimensional view of pore-network model.

图中多孔网络表面的网格为质量扩散层的网格划分，靠近喉道的一侧为细网格，而靠近顶部的一侧为粗网格，质量扩散层代表蒸汽在多孔网络模型外侧的传输，多孔网络内的液相通过蒸发作用扩散到表面。在蒸发过程中可以观察到三种类型的孔隙：部分充满液相的孔隙，此类孔隙中含有静止或者移动的气液两相界面；完全充满气相的空孔隙；完全充满液相且其相邻孔隙均非空的孔隙。

在多孔网络中，蒸汽传输由扩散作用占主导，可用菲克定律描述蒸汽传输过程。在充满气体的区域，蒸汽从孔隙i传输到相邻孔隙j的扩散速率方程见式（1）～式（4）。

多孔网络模型中每个空孔隙均应满足蒸汽浓度质量守恒方程，见式（5）。

多孔网络模型与质量扩散层交界面处的孔隙i及其相邻质量扩散层中的网格单元j的蒸汽浓度由式（6）确定。

将液体在多孔网络中的流动假设为充分发展的层流。孔隙与相邻孔隙的液体流量由哈根泊肃叶定律确定，见式（7）～式（10）。

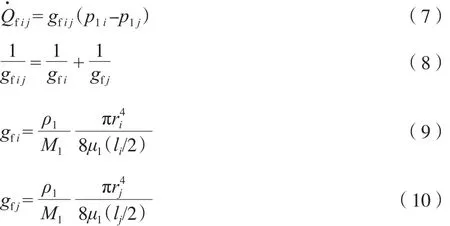
在蒸发过程中，弯液面的移动取决于每个孔隙的临界压力，当弯液面两侧气液相的压差小于临界压力时，弯液面不会移动。半径为rt的喉道，其临界压力计算见式（11）。

气相从喉道入侵孔体内液相有两种方式，一种为突破入侵，一种为聚合入侵。突破入侵又可分为从孔体到喉道的突破入侵与从喉道到孔体的突破入侵。从孔体到喉道的突破入侵是指当孔体被气相入侵后，与孔体相连的喉道会立即被气相入侵；而从喉道到孔体的突破入侵是指当喉道被气相入侵后，与其相邻的孔体会立即被气相入侵。突破入侵孔体的临界压力计算见式（12）。

聚合入侵孔体的临界压力计算见式（13）～式（16）。

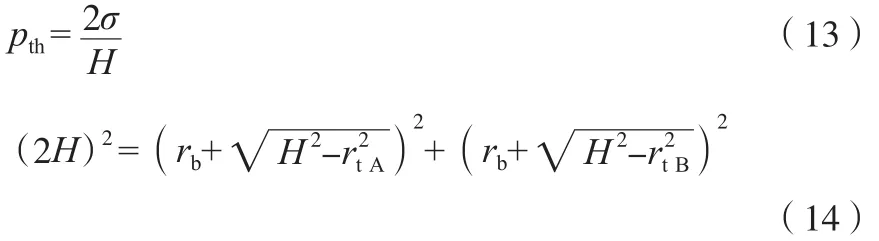
H必须满足式（15）～式（16）。

当式（12）无解时，则气相入侵孔体的方式为突破入侵。

对于完全充满液相的孔体或者含静止弯液面的部分充有液相的孔体，它内部的液相满足质量守恒定律，即式（17）。

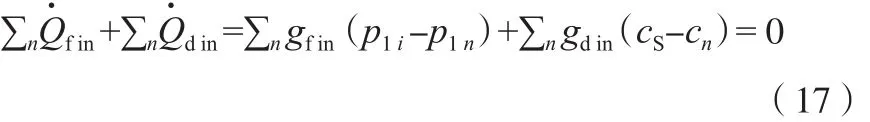
起初，多孔网络模型内部充满液态水，之后水分通过蒸发作用扩散到外界空气中。可应用如下算法模拟多孔网络模型的蒸发过程：1）假设多孔网络模型与质量扩散层交界面的蒸汽浓度为饱和蒸汽浓度；2）基于交界面处的蒸汽饱和度，分别求解多孔网络模型与质量扩散层中的蒸汽浓度场；3）通过多孔网络与质量扩散层中的蒸汽浓度计算交界面处的蒸汽浓度；4）重复步骤2和3，直到交界面处连续两次的蒸汽浓度之差小于1×10-5mol/m3；5）扫描和确认多孔网络模型中所有的液体团，确定每个液体团中具有最低临界压力的孔隙，然后假设这些孔隙中的弯液面移动，其余弯液面均为静止；6）求解多孔网络内液体团的压力分布；7）确定每个静止弯液面的pg-pl-pth值，若该值为正且最大，则假设该弯液面移动；8）重复步骤6和7直至没有弯液面从静止变为移动；9）确定具有移动弯液面的孔隙中液相的蒸发速率，确定每个液体团中完全去除具有移动弯液面的孔隙内的液体所需要的时间，每经过一个时间步长，更新一次多孔网络模型内液体的分布。最小时间步长tcmin，用于更新每个液体团的具有移动弯液面的孔隙内所含有的液体体积满足；12）重复以上步骤直到模型内液态水含量为0。

2 一方程模型

一方程模型是一种经典的连续性模型，该方程中仅含有一个变量——液相饱和度，因而被称为一方程模型。在连续性模型中，液相与蒸汽仅沿着垂直于蒸发面的方向进行传输。液相与蒸汽分别满足质量守恒方程，见式（18）～式（19）。

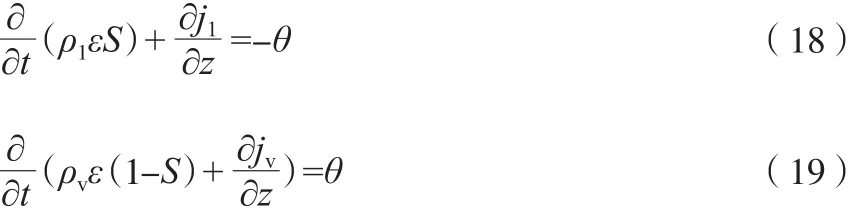
z方向为垂直于蒸发面的高度方向（如图1所示）。j1可按通用达西定律计算，见式（20）。

假设蒸汽与空气的混合气体为理想气体，则jv按式（21）计算。

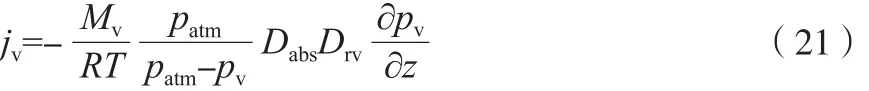
由式（16）与式（19）可得式（22）。

假设气液界面两端满足局部毛细平衡，则毛细力与液相压力满足式（23）。

结合式（20）～式（23），得式（24）。

等式右边括号中的两项分别表示液相、气相在多孔介质中的传输。

式（24）中含有两个变量，分别为S和pv，为了更易于求解式（24），在S和pv间引入式（25）。

将式（25）代入式（24）得式（26）。

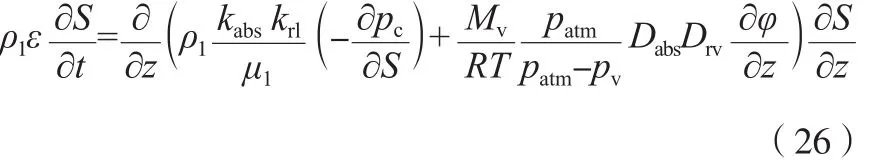
因此，湿分扩散系数按式（27）计算。

最终一方程模型可以简化为式（28）。

3 结果与讨论

为了从孔隙尺度研究单一润湿多孔介质的蒸发特性以及获得不同气相入侵方式时湿分扩散系数的分布，本工作采用了3种多孔网络模型，分别为模型A、模型B与模型C。其中，模型A、模型B在x，y，z方向的孔体个数分别为25，25，40，孔体的边长均为5 μm，喉道的宽度均匀分布在1～3 μm，而孔隙接触角则分别为0°与110°。模型C在3个方向的孔体个数均为20，孔体的边长均为1 mm，喉道宽度均匀分布于0.46～0.50，孔隙接触角为85°。由于孔隙尺寸的分布以及接触角的不同，通过计算可知，模型A与模型B的气相入侵方式为突破入侵占主导，模型C的气相入侵方式则为聚合入侵占主导。模型A、模型B与模型C的孔体与喉道临界入侵压力范围见表1。

表1 模型A、模型B与模型C的孔体与喉道临界入侵压力分布范围Table 1 Distribution range of threshold pressure in pore body and throat for type A，type B and type C

模型A、模型B与模型C的蒸发速率随总体饱和度的变化曲线见图2。

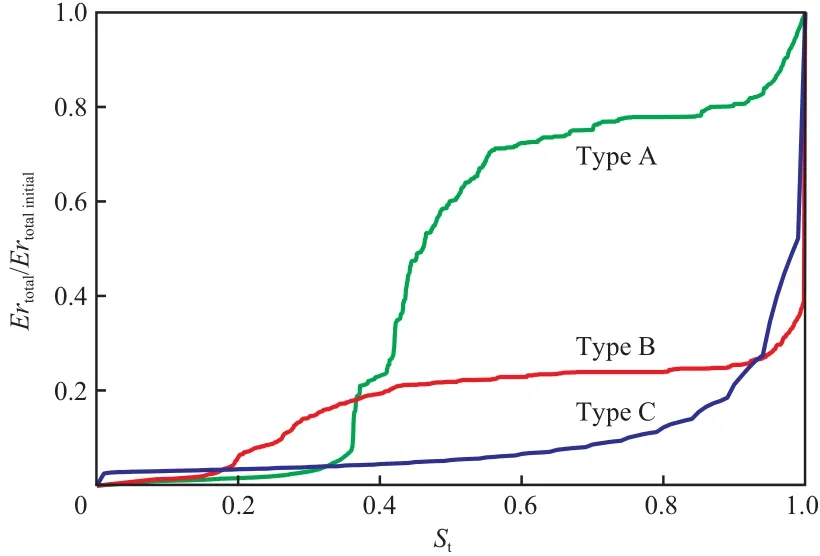
图2 模型A、模型B与模型C的蒸发速率随总体饱和度的变化曲线Fig.2 Variation of evaporation rate with overall saturation for type A，type B and type C.

在模型中，蒸发速率可由第一层喉道与质量扩散层间的蒸汽扩散速率得到。由图2可知，模型A与模型B的蒸发过程均可分为4个阶段，分别为表面蒸发阶段、速度稳定阶段、速度下降阶段与前沿后退阶段，且各模型在各阶段持续的时长不同。模型B在蒸发开始阶段，存在一个速度急剧下降的过程，这是由于喉道的临界入侵压力小于孔体的临界入侵压力，所以在蒸发开始进行时，表层喉道内的液相会优先被气相入侵，导致表层喉道对蒸发速率的贡献减少。对于模型C而言，气相入侵方式由聚合入侵主导，蒸发过程是一个稳定的过程，孔隙内的液相被气相逐层入侵，蒸发前沿稳定后退，蒸发速率随之稳定下降，因而无法观测到速度稳定阶段。

模型A与模型B的气相入侵方式为突破入侵占主导，它们的蒸发过程是一个毛细指进的过程，即气液两相的分布整体上呈现随机的特征，与具有稳定后退前沿的模型C截然不同，因此重点研究了模型A与模型B的蒸发特性。由于孔体与喉道临界入侵压力的差异，导致了孔体与喉道内的液相对蒸发速率的贡献不同。模型A、模型B中孔体与喉道内对蒸发速率的贡献占比见图3。由图3可知，模型A中蒸发速率的贡献主要来自于喉道内的液相，而模型B中蒸发速率的贡献主要来自于孔体内的液相。这是因为模型A的喉道临界入侵压力与孔体的相同，当喉道内的液相被气相入侵后，与它相邻孔体内的液相会立即被气相入侵，由于喉道的数量远多于孔体，因而喉道内的液相对蒸发速率的贡献远大于孔体。而模型B则恰好相反，喉道的临界入侵压力小于孔体，喉道易于被气相入侵，蒸发主要来自于孔体内的液相。

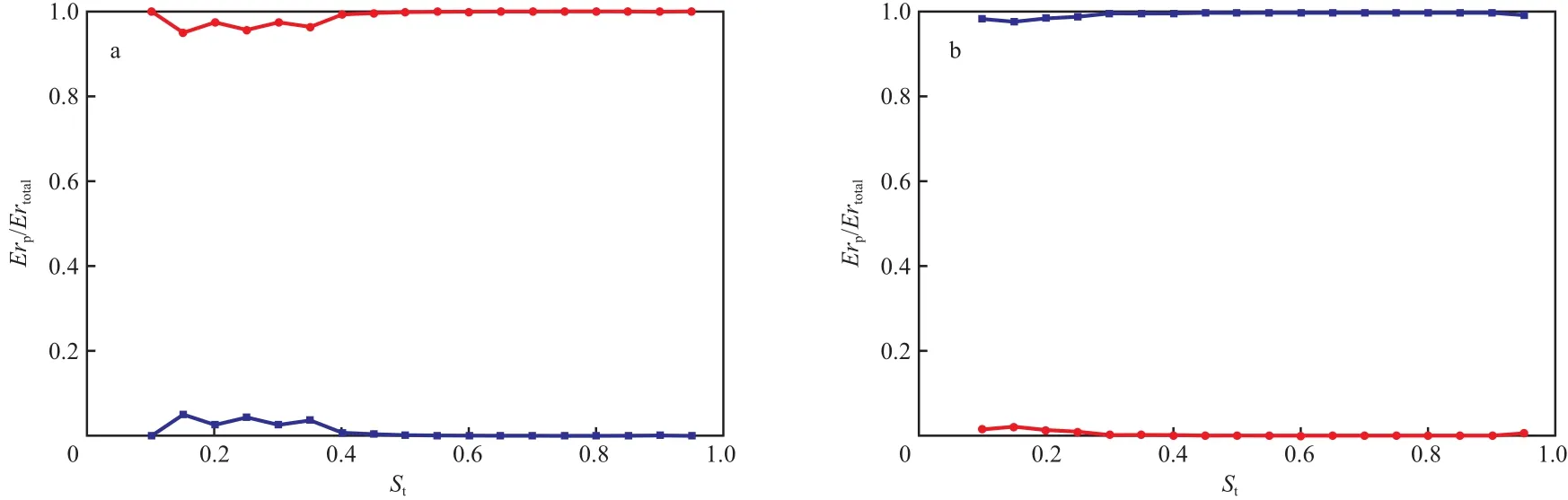
图3 模型A（a）、模型B（b）中孔体与喉道对蒸发速率的贡献占比Fig.3 Contribution to evaporation rate from pore body and throat for type A(a) and type B(b).

表层孔隙作为最靠近外侧质量扩散层的孔隙，对蒸发速率的贡献尤为重要。模型A、模型B表层孔隙对蒸发速率的贡献占比见图4。其中，模型A的表层指表面第一层喉道，而模型B由于在蒸发开始进行时，表面第一层喉道内的液相全部被气相入侵，在表面第一层喉道对蒸发速率的贡献为0，因而统计的是第二层孔体对蒸发速率的贡献占比。由图4可见，在表面蒸发阶段与速度稳定阶段，蒸发主要来自于表层孔隙，而蒸发由速度稳定阶段进入速度下降阶段，正是由于表层孔隙蒸发速度下降造成的。

图4 模型A、模型B表层孔隙对蒸发速率贡献的占比Fig.4 Contribution to evaporation rate from surface layers for type A and type B.

为了探索不同气相入侵方式时的湿分扩散系数与局部饱和度间的关系，对不同的多孔网络模型采用有限差分法计算了一方程模型中的湿分扩散系数。通过对多孔网络模型沿垂直于蒸发面的方向即z方向进行分层，以不同层数的孔隙作为一个控制体，以每个控制体的中心点作为计算节点，应用有限差分法求解各个控制体中的湿分扩散系数。首先，对一方程模型沿z方向进行积分得式（29）。

时间项采用向前差分的方式计算，见式（30）。

空间项沿z方向向前差分，得式（31）。

一方程模型中，湿分扩散系数既包括了液相沿垂直于蒸发面方向的扩散，也包括了蒸汽沿该方向的扩散，因而式（29）中的液相饱和度同样包括了液相与蒸汽，在本文中，控制体中的蒸汽浓度通过质量守恒转换成同等质量的液相，并换算成液相饱和度。

模型A与模型B在z方向的孔体个数为40，分别选取1，2，5，8层孔隙作为一个控制体计算相应的湿分扩散系数，而模型C在z方向的孔体个数为20，则分别选取1，2，4，5层孔隙作为一个控制体进行计算。时间项中时间间隔取整体液相饱和度减少0.01时所需的时间间隔，如整体液相饱和度由0.95减少到0.94时所需的蒸发时间作为对应两个时刻的时间间隔。当控制体选取不同层数的孔隙时，湿分扩散系数的分布整体上呈现相似的规律，因而本研究仅展现了控制体层数为5层时湿分扩散系数的分布。图5为模型A、模型B和模型C在取5层孔隙作为控制体时湿分扩散系数随控制体内液相饱和度（局部液相饱和度）的变化。表2为各模型的湿分扩散系数与局部液相饱和度在不同区间拟合的函数关系式。由图5可知，模型A与模型B的湿分扩散系数总体上先随局部液相饱和度的减少而减少，到达某一临界局部液相饱和度后，湿分扩散系数随局部液相饱和度的减少而增加。这是由于当液相饱和度较高时，多孔网络模型中存在着较大的连续液团，湿分主要通过这些大型的连续液团进行传输，此时湿分扩散系数较大。随着蒸发的进行，大型的连续液团被分割成间断的小型液团，湿分的液相传输通道断裂，湿分扩散系数减小。随着蒸发的继续进行，控制体中蒸汽浓度偏离饱和蒸汽浓度，蒸汽对湿分传输的贡献逐渐突显。对于模型C而言，由于蒸发过程中存在稳定后退的蒸发前沿，因而随着控制体中局部液相饱和度的减少，液相饱和度的空间梯度也减小，即式（27）中分母项减小，湿分扩散系数增大。

图5 模型A（a）、模型B（b）和模型C（c）在控制体取5层孔隙时，湿分扩散系数随局部液相饱和度的变化Fig.5 Variation of moisture diffusivity with local saturation for type A(a)，type B(b) and type C(c) as the layer of control volume equals 5.

表2 模型A、模型B和模型C在控制体取5层孔隙时，湿分扩散系数与局部液相饱和度间的函数关系式Table 2 Function between moisture diffusivity and local saturation for type A，type B and type C as the layer of control volume equals 5

在一方程模型中，若能已知湿分扩散系数与边界条件，即可求解一方程，获得液相饱和度随时间与空间的变化关系。因此，求解了各个模型在控制体取不同层数的孔隙时，表面蒸汽浓度与表层控制体局部液相饱和度的关系，并用相同的函数形式进行了拟合。

图6为各模型在控制体取5层孔隙时，表面蒸汽浓度随表层控制体局部液相饱和度的变化。因模型B中表层孔隙内的液相在蒸发开始进行时就被气相入侵，因而在模型中可获取的表层控制体局部液相饱和度最大值为0.75。表3为表层蒸汽浓度与表层控制体局部液相饱和度间拟合的函数关系式。

通过拟合湿分扩散系数与局部液相饱和度间的关系以及表层蒸汽浓度与表层控制体局部液相饱和度间的关系（见表2和表3），分别获得了一方程模型中的湿分扩散系数与边界条件，是后续求解一方程模型、反推多孔介质蒸发过程的基础。

图6 模型A、模型B与模型C在控制体取5层孔隙时，表面蒸汽浓度随表层控制体局部液相饱和度的变化Fig.6 Variation of surface vapor concentration with local saturation in surface control volume for type A，type B and type C as the layer of control volume equals 5.

表3 模型A、模型B与模型C在控制体取5层孔隙时，表面蒸汽浓度与表层控制体局部液相饱和度间的关系Table 3 Function between surface vapor concentration and local saturation in surface control volume for type A，type B and type C as the layer of control volume equals 5