火龙果片微波间歇干燥特性及其动力学研究

盘喻颜段振华刘 艳唐小闲李定金

(1. 贺州学院食品与生物工程学院，广西 贺州 542899；2. 大连工业大学食品学院，辽宁 大连 116034； 3. 广西果蔬保鲜和深加工研究人才小高地，广西 贺州 542899)

火龙果又称仙蜜果，源于中美洲，目前中国主要分布在广西、福建、台湾、云南等地[1]。火龙果不但富含多种维生素、氨基酸、矿物质等，且含其他植物体内稀有的花青素及植物性白蛋白，是兼备高营养和低热量的水果，具有预防重金属中毒、增强骨质、降低胆固醇等作用[2-3]。

火龙果以鲜食为主，含大量水分，易引发腐败变质，不利于运输与贮藏。干燥作为食品保存和加工应用的常见方式，是通过脱除物料中的水分，从而限制微生物和化学反应，具备便于产品流通、延长贮藏期等优点，能有效解决水果贮藏期太短而造成浪费的问题[4]。现有关于火龙果干燥的研究较少，陈晓旭等[5]、邹同华等[6]研究了火龙果热风联合变温压差膨化干燥、真空冷冻干燥工艺的优化。Yi等[7]研究了微波联合变温压差膨化干燥对火龙果片胞壁多糖改性、理化性质的影响。Nordin等[8-9]研究了关于微波干燥对火龙果片理化性质、质构、显微结构及复水性的影响。总体上看，已有关于火龙果冷冻干燥、热风联合变温压差膨化干燥工艺的优化以及微波及其联合干燥对火龙果品质影响的报道[10-11]，但火龙果微波干燥工艺的优化及动力学研究未见报道。动力学模型的研究作为加工过程中预测水分含量与干燥用时的重要理论依据，缺少相应的理论依据会限制微波干燥在火龙果中的实际应用，所以研究火龙果微波干燥动力学具有重要的意义。

微波干燥有独特的内部加热模式，省时节能、保质降本、环保易控[10-11]，因此被广泛应用于农产品加工保藏及食品工业生产中，包括罗非鱼[12-13]、马蹄淀粉[14]、山药[15]、黄秋葵[16]、花椒[17]、银杏果[18]、枸杞[19]等加工领域，但单纯使用微波技术进行干燥，易使局部温度过高，导致物料出现边缘焦糊和硬化等现象，为保证产品品质，防止局部过热则要探索微波在干燥工艺上的创新。采用微波间歇干燥，能有效均衡水分分布和温度情况，从而避免出现过热导致烧伤[14]。本试验拟以火龙果为原料，研究火龙果片在微波间歇干燥条件下的干燥特性，并根据试验数据建立了火龙果片微波间歇干燥的动力学模型，意为火龙果片微波间歇干燥的相关基础研究、工艺设计及参数优化提供参考，解决水果因贮藏期太短而造成浪费的问题。

1 材料与方法

1.1 材料与主要仪器

1.1.1 材料

火龙果：红肉火龙果，购于贺州泰兴超市。

1.1.2 主要仪器设备

电子天平：JJ1000型，常熟市双杰测试仪器厂；

水分测定仪：MA150 Starorius型，北京赛多利斯仪器系统有限公司；

微波炉：G70D20CN1P-D2(S0)型，广东格兰仕微波电器制造有限公司。

1.2 方法

1.2.1 预处理 火龙果经人工去皮后切成一定厚度的火龙果片，5%的NaCl溶液浸泡2 min后，沥水10 min备用。

1.2.2 微波功率 取60.0 g火龙果片切成6 mm薄片，加热1 min，间歇1 min，选择不同功率(350，420，490 W)进行微波间歇干燥试验，测定并记录干燥过程中间歇时间下火龙果片质量，直至干燥至干基含水量≤15%为止。

1.2.3 切片厚度 每次取60.0 g火龙果片，微波功率420 W，加热时间1 min，间歇时间1 min，选择不同切片厚度(3，6，9 mm)的火龙果片进行微波间歇干燥试验，测定并记录干燥过程中间歇时间下火龙果片质量，直至干燥至干基含水量≤15%为止。

1.2.4 加热时间 每次取60.0 g火龙果片，微波功率420 W，切片厚度6 mm，加热时间1 min，间歇时间1 min，选择不同加热时间(0.75，1.00，1.25 min)进行微波间歇干燥试验，测定并记录干燥过程中间歇时间下火龙果片质量，直至干燥至干基含水量≤15%为止。

1.2.5 间歇时间 每次取60.0 g火龙果片，微波功率420 W，切片厚度6 mm，加热时间1 min，选择不同间歇时间(0.50，0.75，1.00 min)进行微波间歇干燥试验，测定并记录干燥过程中间歇时间下火龙果片质量，直至干燥至干基含水量≤15%为止。

1.3 指标

1.3.1 含水量的测定 采用水分测定仪进行测定。火龙果片初始含水率的平均测定值为86.81%，任一时刻火龙果干基含水率按式(1)计算。

1.3.2 干基含水率计算

(1)

式中：

M——干基基含水率，g/g；

mt——湿物料质量，g；

m——绝干物料质量，g[11]。

1.3.3 干燥速率计算

(2)

式中：

DR——干燥速率，g/(g·min)；

Δt——两次相邻时间之差，min；

m——绝干物料质量，g；

△m——两次相邻质量之差，g[15]。

1.3.4 水分比计算

(3)

式中：

MR——水分比；

M0——初始含水率，%；

Mt——干燥中某时刻的含水率，%；

Me——平衡含水率(远远小于M0和Mt，通常忽略不计)，%[20-21]。

1.3.5 干燥模型拟合 本试验筛选了5种常见干燥模型来拟合火龙果片的干燥模型。对其进行线性化处理以便统计分析和数据处理，如表1所示[14]。

表1 5种干燥模型及表达式†

†k、n、a、b、c均为表达式中的待定系数；t为时间，min。

1.4 数据分析

最终试验结果为3组平行试验的平均值；SPSS 17.0进行线性回归和求得模型方程的待定系数，Excell 2010进行数据分析，Origin 2017绘图。

2 结果与分析

2.1 火龙果片微波间歇干燥特性

2.1.1 微波功率对火龙果片干燥特性的影响 由图1可知，随着微波功率的增大，火龙果片的干燥曲线变化越陡峭，所需干燥时间越短，微波功率为490，420，350 W时，干燥时间分别为22，30，38 min。这是因为在固定其他条件不变时，火龙果片中水分子吸收的微波随着微波功率增大而增加，加剧了火龙果片内部振荡，加快了干燥速度，所需的干燥时间就越少。因此，在一定的微波功率范围内，适当地提高微波功率可以缩短干燥时间。

图1 火龙果片在不同微波功率下的干燥曲线

由图2可知，火龙果片微波间歇干燥过程包括前期加速、中期恒速和后期降速阶段。火龙果片的干燥速率曲线随微波功率的增大而变陡峭。干燥前期，火龙果片含有大量水分，能够吸收大量微波，干燥速率呈上升趋势；干燥中期，火龙果片吸收的微波均用于蒸发内部的大部分水分，干燥速率保持恒定状态；干燥后期，随着火龙果片内部水分子的减少，吸收的微波也减少，干燥速率呈下降趋势[22]。

图2 火龙果片在不同微波功率下的干燥速率曲线

2.1.2 加热时间对火龙果片干燥的影响 由图3可知，火龙果片的干燥曲线随着加热时间的延长而变陡峭，所需的干燥时间缩短，加热时间为1.25，1.00，0.75 min时，干燥时间相差不大。原因可能是加热时间越长，增加了火龙果片内的水分子的振荡时间，增大了干燥速率，所需干燥时间就越短。因此，在一定加热时间范围内，可通过增大加热时间来提高干燥速率。

图3 火龙果片在不同加热时间下的干燥曲线

由图4可知，在微波间歇干燥过程中，干燥速率曲线随着加热时间的延长而越陡峭；由前期加速和后期降速阶段组合而成，而中期恒速阶段不明显。原因是随着加热时间的延长，火龙果片中大量的水分在升温阶段之初就已脱除，所以当加速阶段的干燥速率达到极大值时，火龙果片吸收微波的能力明显下降，干燥速率呈下降趋势，因此恒速阶段不明显。

图4 火龙果片在不同加热时间下的干燥速率曲线

2.1.3 间歇时间对火龙果片干燥的影响 由图5可知，火龙果片的干燥曲线随着间歇时间的延长而变平缓，所需的干燥时间增加。间歇时间为0.50，0.75，1.00 min时，所需的干燥时间为19.50，26.25，36.00 min。随着微波加热的进行，火龙果片内部温度急剧上升，造成局部过热，导致火龙果片烧焦。因此在微波加热时增加间歇这一步骤，可以有效防止火龙果片烧焦，充分脱除内部水分，通过减少微波加热时间，降低能耗。

由图6可知，在微波间歇干燥过程中，干燥速率曲线随着间歇时间的增加而变平缓。由于火龙果片中的水分子在微波作用下，摩擦生热从而达到干燥的目的，但间歇时间内没有微波的辅助，只能依靠残留的热能进行干燥，所以间歇时间越长，干燥时间越久。因此，在一定间歇时间范围内，可通过缩短间歇时间来提高干燥速率。

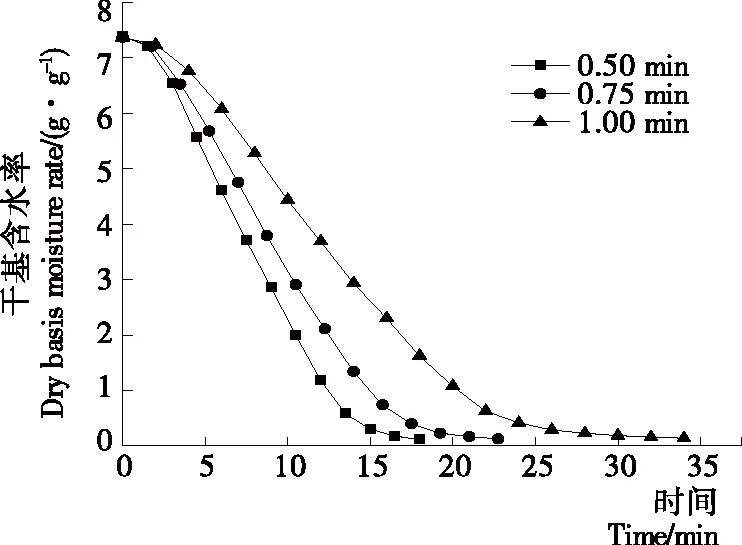
图5 火龙果片在不同间歇时间下的干燥曲线

图6 火龙果片在不同间歇时间下的干燥速率曲线

2.1.4 切片厚度对火龙果片干燥特性的影响 由图7可知，随着切片厚度的增大，火龙果片的干燥曲线变化越平缓，所需的干燥时间越长。切片厚度为3，6，9 mm时，所需的干燥时间分别为26，38，48 min。这是由于火龙果片的厚度决定了内部水分迁移的距离，火龙果片越薄，内部水分迁移的距离就越小，干燥所需的时间就越短；火龙果片越厚，内部水分迁移的距离就越大，内部传热传质阻力越大，所需的干燥时间就越长[23]。因此，在一定的切片厚度范围内，适当减小切片厚度可以缩短干燥时间。

图7 火龙果片在不同切片厚度下的干燥曲线

由图8可知，在微波间歇干燥过程中，随着切片厚度的减小，干燥速率曲线变化越陡峭，中期恒速阶段越不明显。这是由于火龙果片的加热过程是内外同时进行，随着切片厚度的减小，从外到内热量传递的距离减小，从内到外水分迁移的距离也减小，加快了热量和水分的传递速度，从而增大了干燥速率。

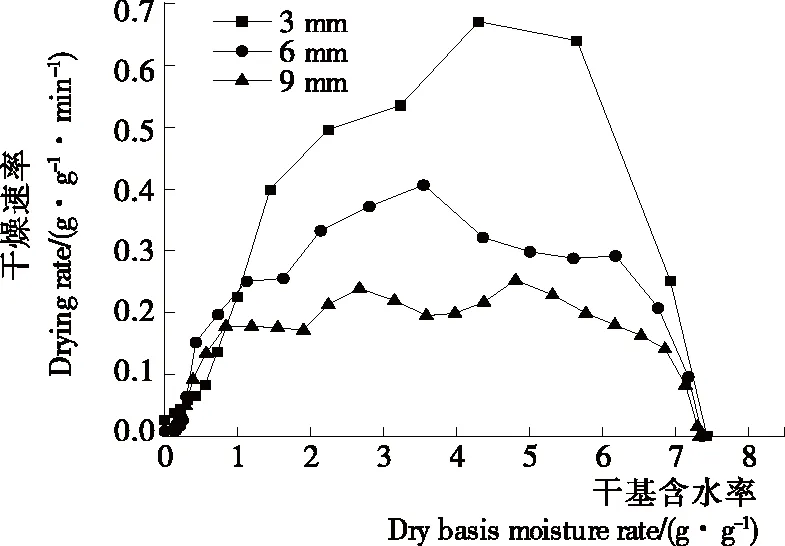
图8 火龙果片在不同切片厚度下的干燥速率曲线

2.2 火龙果片微波间歇干燥动力学

2.2.1 模型的选择 在筛选的5种模型中Wang-Singh模型的MR—t为线性关系，Lagarithmic、Henderson-Pabis、Newton3种模型的-lnMR-t均为线性关系，Page模型的ln(-lnMR)-lnt为线性关系，所以以MR、-lnMR、ln(-lnMR)为纵坐标，t、t、lnt为对应的横坐标，分别绘制不同微波功率、加热时间、间歇时间、切片厚度下的MR-t、-lnMR-t、ln(-lnMR)-lnt曲线图，如图9～11所示。

由图9可知，Wang-Singh模型不适用于建立目前模型，因为相关变量下MR-t是非线性关系，通过分析计算可知，Wang-Singh模型拟合方程的R2=0.943。

由图10可知，这3种模型均不适用于建立目标模型，因为相关变量下-lnMR-t是非线性关系，通过分析计算可知，Logarithmic模型拟合方程的R2=0.964，Handerson and Pabis模型拟合方程的R2=0.935，Newton模型拟合方程的R2=0.908。

由图11可知，在所筛选的模型中，只有相关变量下ln(-lnMR)-lnt呈线性关系，通过分析计算可知，Page模型拟合方程的R2=0.991，优于前面4个模型所得的R2值，表明Page的模型能更好地适应所有干燥条件，所以采用Page模型作为火龙果片微波干燥动力学模型。

Page模型：ln(-lnMR)=lnk+nlnt，令：

lnk=a+bP+cH+dX1+eX2，

(4)

n=f+gP+hH+iX1+jX2，

(5)

式中：

P——微波功率，W；

X1——加热时间，min；

X2——间歇时间，min；

H——切片厚度，mm；

a、b、c、d、e、f、g、h、i、j——待定系数。

图9 火龙果片在不同因素下MR与t的关系曲线

图10 火龙果片在不同因素下-lnMR与t的关系曲线

图11 火龙果片在不同因素下ln(-lnMR)与lnt的关系曲线

可得到：

ln(-lnMR)=a+bP+cH+dX1+eX2+(f+gP+hH+iX1+jX2)lnt。

(6)

将不同功率、不同加热时间、不同间歇时间、不同切片厚度试验所得的数据依次代入，由SPSS 17.0进行多元线性回归求得方程线性拟合各待定系数，为a=-5.95，b=0.008，c=-0.458，d=1.578，e=-1.314，f=2.441，j=-0.373，h=0.056，i=-0.458，g=0.000。

得拟合方程：

ln(-lnMR)=-5.95+0.008P-0.458H+1.578X1-1.314X2+(2.441+0.056H-0.458X1-0.373X2)lnt，

(7)

即

MR=e-ktn，

(8)

式中：

k=e-5.95+0.008P-0.458H+1.578X1-1.314X2；

n=2.441+0.056H-0.458X1-0.373X2。

该拟合方程的F为2 192.294，显著性水平P<0.001，R2=0.991，表明该方程极显著且拟合度较高。

2.2.2 模型的检验 如图12所示，设定条件为功率420 W，加热时间1 min，间歇时间1 min时，切片厚度6 mm，试验值与拟合值有较高的拟合度，Page模型适用于描述和预测火龙果片微波间歇干燥过程中水分变化和干燥用时情况。

3 结论

试验表明，火龙果片微波间歇干燥包括加速、恒速和降速阶段，其中切片厚度，间歇时间与干燥速率、物料脱水量呈负相关，与干燥时间呈正相关。加热时间、微波功率与干燥时间呈负相关，与干燥速率、物料脱水量呈正相关，其中加热时间对火龙果片微波间歇干燥速率的影响较小。比较了5种常见的干燥模型,经拟合得到火龙果片微波间歇干燥的最佳模型为Page模型。但本试验所用的火龙果片为了之后的工艺优化均用5% NaCl浸泡过，可能会与鲜果存在一定差异，批量生产时应做小批量的预试验。

图12 Page模型的拟合值与试验值的比较