基于小波降噪和灰色神经网络的车辙深度指标预测

肖志军

(上海市市政公路工程检测有限公司， 上海 200031)

路面使用性能指标是高速公路维修、养护的重要参考指标。根据高速公路路面使用现状，对高速公路路面性能指标进行预测，是高速公路养护维修部门一项重要的工作内容[1]。车辙是高速公路的主要病害之一，也是路面使用性能重要指标之一[2]。车辙深度达到一定程度不仅影响行车舒适性，还严重威胁行车安全，因此有必要对高速公路车辙深度进行检测、评价和预测，为科学养护和及时维修提供客观依据[3]。

灰色系统分析是我国学者邓聚龙教授于20世纪80年代前期提出的用于控制与预测的新理论、新技术,由于它在建模、预测、控制等方面的独到之处，已在各个方面得到了广泛应用[4]；人工神经网络是近年来发展起来的模拟人脑生物过程的人工智能技术,它由大量简单的神经元广泛互连形成的复杂的非线性系统，具有很强的非线性映射能力，特别适合于因果关系复杂的非确定性推理、判断、识别和分类等问题[5]。

本文研究采用改进型灰色理论GM(1，1)与神经网络模型相结合的方式，对路面使用性能指标(以车辙深度指标为例)进行预测，并且与常规的公式拟合法进行分析比较。为了避免检测数据的变异及噪声影响，尽量提高数据预测的准确性和有效性，本文先采用小波理论对检测指标进行降噪预处理。

1 基本理论

1.1 小波降噪分析

在小波函数中应用很广泛的Daubenchies小波是Daubechies从2尺度方程系数出发设计出来的离散正交小波。一般简写为dbN，N是小波的阶数[6]。本文选用db3小波函数对路面车辙深度数据进行降噪分析。

如何选取阈值是进行信号降噪处理的关键,它直接关系到信号的质量[7]。本文对阈值的选取,采用基于Stein的无偏似然估计(SURE)的软阈值估计(rigsure)。该方法利用实际降噪处理过程中的经验公式给出阈值，往往比默认阈值更具有可信度[8]。

1.2 改进型GM(1，1)

通常GM(1，1)模型通过对数列的不同取舍，可得到一系列预测结果，而组成一个预测灰区间供决策选用[9]。但如果GM(1，1)模型预测所得灰区间过大，那么就很难得到较为满意的结果。因此，用已知序列建GM(1，1)模型进行预测时，建议不用这个模型一直预测下去，而是只预测一个值，然后将这个灰数补充在已知数列之后，同时为不增加序列长度，去掉第一个已知数据，以保持数据列的等维，提高模型精度[10]。

这种改进的模型及时补充和利用了新的信息，提高了灰区间的白化度。显然，用改进后的模型去预测一步模型做一次修正，因而预测值都产生在动态之中。随着递补次数的增加灰度也在增加，信息量会越来越少。

1.3 径向基函数神经网络

径向基函数(Radial Basic Function，简称RBF)作为神经网络中的一种模型，广泛应用于模式识别、分类及函数逼近等方面[11]。

RBF神经网络通常由3层组成：输入层、隐层、输出层，其结构如图1所示。图1中，xi为输入变量，wij为权重系数，yj为输出变量[12]。

图1 RBF神经网络结构Fig.1 RBF neural network structure

输入层节点只传递输入信号到隐层，隐层节点由像高斯函数那样的辐射状作用函数构成，而输出层节点通常是简单的线性函数。隐层节点中的作用函数(基函数)对输入信号将在局部产生响应，即：当输入信号靠近基函数的中央范围时，隐层节点将产生较大的输出[13]。因此，径向基函数网络具有较强的局部逼近能力。

2 车辙深度数据小波预处理

路面车辙深度(RD)数据的自动采集中，通常采用在车辆上安装测量设备和传感器的方法，先通过测取车辆匀速行驶时车体特定部位的振动响应信号，再通过功率谱分析，获得车辙在空间频域的分布情况[14]。但由于车辆振动响应为间接获得的一种对路面的反应，所以存在随机性和不稳定性等因素，获取的信号中夹杂噪声信号[15]。如果直接对数据进行指标预测，数据噪声的影响不可避免。采用小波分析来处理车辆振动响应信号，可有效降噪，降噪之后的数据在指标预测中的精度也更高，相对误差也更小。

以S32申嘉湖高速公路浦东段为例来说明基于小波分析的RD数据的处理，任意选取1 km的车辙深度数据为原始数据，经小波分析处理后，其结果如图2所示。

经小波分解与重构后，车辙深度原始数据与降噪之后的数据前后对比结果如图3所示。

从图2、图3中可以看出，3尺度上的近似部分是主要趋势信息，细节部分对应噪声型号。经过3次分解，得到比较平滑的图形，这有利于预测。另外，从细节部分的信息看，在尺度分解中的原始型号随着分解层数的增加，它所包含的高频信息会随之减小。当分解到下一个层次时，就有更高一些的频率信息被滤掉，而所剩下的就是信号发展趋势。

3 车辙深度指标预测分析

3.1 灰色神经网络组合预测方法

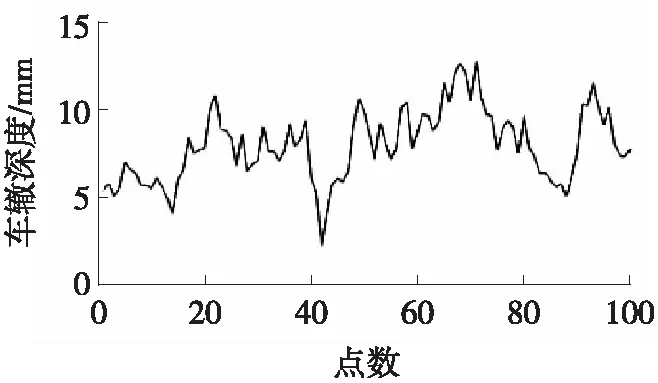
(a) 2018年RD检测数据

(b) 3尺度上的近似部分

(c) 1尺度上的细节部分

(d) 2尺度上的细节部分

(e) 3尺度上的细节部分

(f) 对原数据进行重构

图3 车辙深度原始数据与降噪之后对比Fig.3 Comparison of raw data and data after noise reduction for rutting depth

综上所述，灰色理论算法与神经网络组合预测流程如图4所示。

图4 灰色理论与RBF神经网络组合预测流程Fig.4 Combination forecasting process of grey theory and RBF neural network

3.2 车辙深度指数(RDI)预测

以S32申嘉湖高速公路浦东段和G60沪杭高速公路上海段为例，2条高速公路分别各任意选取2条路段的车辙深度数据为原始数据，经小波降噪处理后，采用上述灰色理论与RBF神经网络组合预测方法预测2018年车辙深度指数RDI，预测结果分别如表1～表4和图5、图6所示。

3.3 不同预测方法比较

把回归拟合公式法和改进型GM(1，1)与神经网络组合法2种方法对同一路段RDI数据的预测值与实测值进行对比，可以判断这2种方法的优劣性。从表1～表4可以看出，改进型GM(1，1)与神经网路组合法较回归拟合公式法预测值更接近实测值，相对误差普遍更小。

表1 S32路段一车辙深度指标预测Table 1 RDI prediction for section one in S32 expressway

注：null表示该年份数据缺失；R2为拟合回归公式的相关系数；y代表年数，下同。

表2 S32路段二车辙深度指标预测Table 2 RDI prediction for section two in S32 expressway

表3G60路段一车辙深度指数预测
Table 3RDIprediction for section one in G60 expressway

方法20112012201320142015201620172018(预测)2018(实测)相对误差/%改进型GM(1,1)与神经网络法RD6.266.456.477.08nullnull7.78.058.2-1.83RDI87.587.18785.8nullnull84.683.983.60.36拟合回归公式法RDRDIRDI= 100/[1+ 0.135 9·exp(0.041 99·y)] R2:0.950 18.08.2-2.4484.083.60.48

表4 G60路段二车辙深度指数预测Table 4 RDI prediction for section two in G60 expressway

(a) 路段一

(b) 路段二

(a) 路段一

(b) 路段二

4 结束语

通过采用小波理论对路面车辙深度指数进行降噪预处理，本文建立的基于改进型GM(1，1)灰色理论与神经网络相结合的高速公路路面性能指标预测方法，与常规回归拟合公式预测方法比较可以看出：前者准确性更高，相对误差更小。

影响路面使用性能指标衰变的因素极其复杂，同一路段的历年实测数据经常会出现不同程度的波动，此时传统公式预测方法的适用性就会较差。本文提出的改进型灰色理论与RBF神经网络模型相结合的方法，通过不断学习和修正预测值与实测值之间的相对误差来提高预测精度，具有一定的工程应用价值。随着样本数据库的逐渐补充和完善，该方法还可进一步提高预测准确性和有效性。