含忆阻器的并联混沌电路动力学分析

方 淼，谢苗苗，方 鸣

（安徽大学江淮学院理工部，安徽合肥230039）

忆阻器是蔡少棠在1971年提出的具有记忆特性的非线性电阻器[1]，由Strukov等在物理上成功实现的第4种基本无源二端口元件[2]，在混沌保密通信、混沌系统控制和图像加密中具有重要的应用价值[3-4]。忆阻器具有非线性特性，基于忆阻器构成的忆阻电路容易产生非线性混沌振荡，因此基于忆阻器的连续混沌电路模型的设计引起了国内外学者的关注，各种混沌电路被相继提出，为混沌理论的实际应用奠定了基础。Itoh等采用分段线性忆阻器代替Chua混沌电路中的蔡氏二极管建立了振荡电路[5]；Buscarino等基于惠普忆阻器的实物模型设计了一种新型忆阻混沌电路[4]；Bao等提出光滑连续的三次单调上升的非线性归一化磁控忆阻器，并基于该模型设计出忆阻混沌电路[6]。以上忆阻混沌电路均是基于蔡氏电路设计的，电路结构较复杂，且产生的混沌吸引子和Chua混沌吸引子相似。Muthuswamy等设计并实现了仅由电感、电容和忆阻器串联构成的最简串联忆阻混沌电路[8]；许碧荣随后采用三种元件并联设计构建了最简并联忆阻混沌电路，并进行了电路实现[9]。但这些电路只能产生简单的单涡卷混沌吸引子，且其中的动力学特性未得到详细的分析和研究。

因此如何利用忆阻器构建电路结构简单、具有丰富动力学现象的非线性动力系统成为研究热点。基于此，本文提出一种有源压控忆阻器的数学模型，利用该忆阻器和电容、电感并联构成一个简单并联混沌电路系统，建立该系统的无量纲数学模型，通过数值仿真研究该系统的动力学行为。

1 并联混沌电路系统模型

1.1 忆阻器

蔡少棠于1971年根据电路的完备性提出忆阻器[1]，在2008年HP实验室成功实现HP TiO2忆阻器，之后蔡少棠等又对忆阻器[10]的概念进行了拓展，定义为

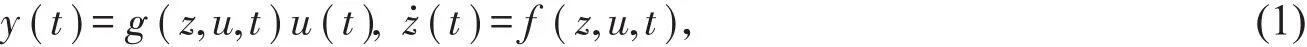
式中，y(t)和u(t)分别表示任意两个互补的基本变量（即电压、电流、磁通和电荷），分别作为忆阻器的输出和输入信号，z表示忆阻器内部状态变量，f是一个连续的n维向量函数，g表示n维的响应函数。根据该定义，若输入信号u(t)为电流，则称为流控型忆阻器；若输入信号u(t)为电压，则称为压控型忆阻器。本电路中采用了压控型忆阻器，并根据忆阻器概念假设该忆阻器的关系式为

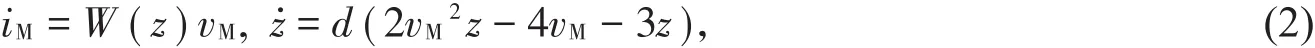
其中，W(z)=c(z2-2z-1)，c，d均为常数。当取c=0.3、d=0.5时，压控忆阻器的忆导W(z)-z的关系如图1(a)所示。从图1(a)可见，该压控忆阻器的忆导W(z)随状态变量z的变化存在负值，因此其瞬态功率p(t)=w(ϕ)u(t)2和瞬时能量随着时间的变化也存在负值，根据蔡少棠提出的忆阻器无源定理，可判断(2)式定义的压控忆阻器为有源忆阻器。当给该压控忆阻器的两端施加一个正弦激励电压v=2sin(2πft)，可以得到忆阻器在v-i平面上的伏安关系曲线如图1(b)所示，其伏安特性曲线具有一个斜“8”字形的类紧磁滞回线的形状，该特性和蔡氏忆阻器所描述的特性一致，具有非线性动力学特性。

1.2 电路模型的建立

将该压控型忆阻器和电感、电容并联，构成一个并联型忆阻混沌电路，如图2所示。该电路仅由3个动态元件组成，他们所对应的状态变量分别为vC、iL和z，其中z是压控忆阻器内部的状态变量。

图1 忆阻器的特性曲线。(a)忆导曲线；(b)伏安特性曲线

图2 基于忆阻器的并联混沌电路

运用基尔霍夫电压和电流定律以及元件的伏安关系分析图2的电路，可得电路的状态方程为

设x=vC，y=iL，α =-，γ=d，则(3)式的状态方程可以写为

因此，图2所示的并联混沌电路是一个三维系统，它的动力学特性可由(3)式描述。

选择电路参数使得α=-2，β =4.1，γ=0.5，c=0.3，在初始条件( )0,10-2,0 下，可见系统（3）生成一类新的拓扑结构较复杂的超混沌吸引子，它在相平面上的投影如图3(a)和3(b)所示。图3(a)是混沌吸引子在x-y平面上的投影，是一个单涡卷混沌吸引子；而图3(b)是混沌吸引子在x-z平面一个折叠的双涡卷的混沌吸引子。通过寻找合适的Poincaré截面，能将系统随时间连续变化运动转化为Poincaré截面上的一个离散映射，该映射降低了系统的维数，但仍能保持原有动力学系统的拓扑性质，因此能更好地刻画出该忆阻电路的混沌特性。图4(a)和4(b)分别给出了x=0和z=0截面上的Poincaré映射。显然基于忆阻器的并联混沌电路的Poincaré映射上存在无穷多个密集点，吸引子的轮廓清晰可见，表现出分形的几何特征，进一步说明该系统的混沌特性。利用Jacobi方法计算Lyapunov指数得LE1=0.24，LE2=0.01，LE3=-0.42，由此可计算出相应的Lyapunov维数为dL=2.57，即该系统存在两个正的Lyapunov指数，一个负的Lyapunov指数，同时其Lyapunov指数谱之和为负，可知该电路系统是超混沌振荡的。

图3 混沌吸引子的投影。(a)x-y平面相轨；(b)x-z平面相轨

图4 并联混沌电路的Poincaré映射。(a)x=0截面；(b)z=0截面

2 基本动力学特性分析

2.1 平衡点的稳定性分析

令ẋ=ẏ=ż=0，可求得系统(4)的唯一平衡点E0( )0,0,0，在平衡点处对系统进行线性化，可得（4）式的Jacobi矩阵：

平衡点E0(0,0,0)对应的特征根方程为

解得其特征根为λ1=-3γ,λ2=

很显然，当α＜0且c＞0时，系统的特征根λ2、λ3实部始终大于零，此时系统的平衡点E0( )0,0,0是不平衡的，否则系统是稳定的，无法产生混沌。当选择电路参数使得α=-2，β=4.1，γ=0.5，c=0.3，可求得相应的特征根λ1=-1.5，λ2、3=0.3± 2.85j，λ1为负实根，λ2、λ3是一对实部大于零的共轭复根，此时平衡点是不稳定的鞍焦点，符合混沌产生的平衡点稳定性条件。

2.2 电路参数对系统影响

通过上面的分析可知，随着系统参数的改变，系统平衡点的稳定性也将随之发生改变，该系统将具有不同的动力学特性。因此下文将对于确定的电路参数γ=0.5、c=0.3和初始条件( )0,10-2,0，选择β和α为可变参量，即电感和电容的参数可调，对系统进行动力学分析。

固定β=4.1，当参数α在[-12,-0.1]内变化时，系统的Lyapunov指数谱和状态变量z的分岔图如图5所示。画状态变量z的分岔图选取的Poincaré截面为x=-1，即系统的三维相空间中垂直于x轴的过（-1,0,0）点的平面。由图可见系统的Lyapunov指数谱和Poincaré截面所反映的动力学行为是一致的。

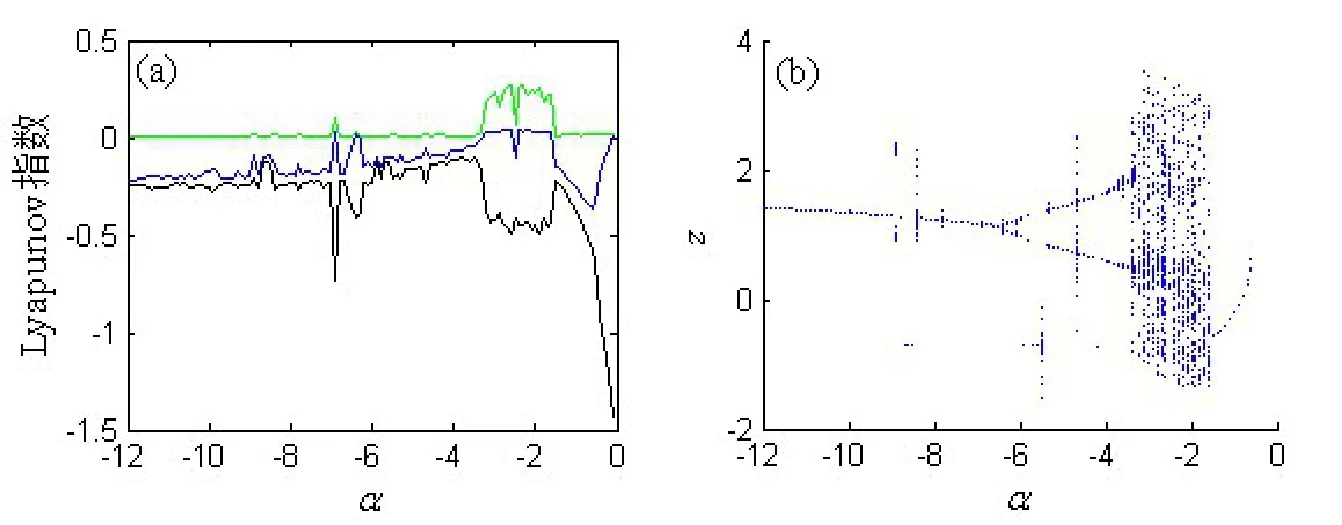
图5 电路参数α变化时Lyapunov指数和分叉图。(a)Lyapunov指数谱；(b)分岔图

当参数α在[-12,-3.22]内时，系统的Lyapunov指数形式为（0，-，-），表明系统处于周期态。当α=-6.358时，系统的Lyapunov指数由负值接近于零，再变为负值，此时系统出现了一次倍周期分岔，从周期1变为周期2。当参数α=-3.22时，系统的Lyapunov指数形式变为（+，+，-），出现了2个正的Lyapunov指数，系统出现了超混沌状态。随后当α=-1.5时，系统的Lyapunov指数形式再次变为（0，-，-），系统由超混沌状态转换为周期态。从图5(b)可见，随着参数α在[-12,-0.1]内逐渐递增，系统(4)从稳定的周期1轨道经倍周期分岔变为周期2轨道，当α=-3.22时系统发生瞬态超混沌进入超混沌轨道，最后由于混沌危机导致运动轨迹发生突变，变成周期1轨道。由于忆阻混沌电路的动力学行为极端依赖于忆阻器的状态变量，导致了忆阻混沌电路出现了不同于一般混沌电路的特殊动力学行为。当α∈(-3.22,-1.56)时系统不全处于混沌态，在[-5.95,-5.8]，[-5.73,-5.57]，[-4.26,-4.18]3个区域内，系统的运动轨道进入周期窗口，从周期2极限环突变为稳定的周期1轨道，系统经过了多次混沌轨道与周期窗口的切换。随着参数α的变化，系统详细的稳定与不稳定区域如表1所示。

表1 随着参数α变化的系统动力学行为

选取不同的参数α，状态变量y，z随α变化的几种典型的相图如图6所示。图6中的(a)和(b)分别为系统的周期1极限环和发生倍周期分岔后的周期2极限环，此相轨图再次证明了该有源压控忆阻器在正弦激励下的滞回特性。图6（c）为系统的另一种周期2极限环，当α的值进一步增大，系统进入混沌状态。混沌吸引子的相轨图如图6(d)所示。

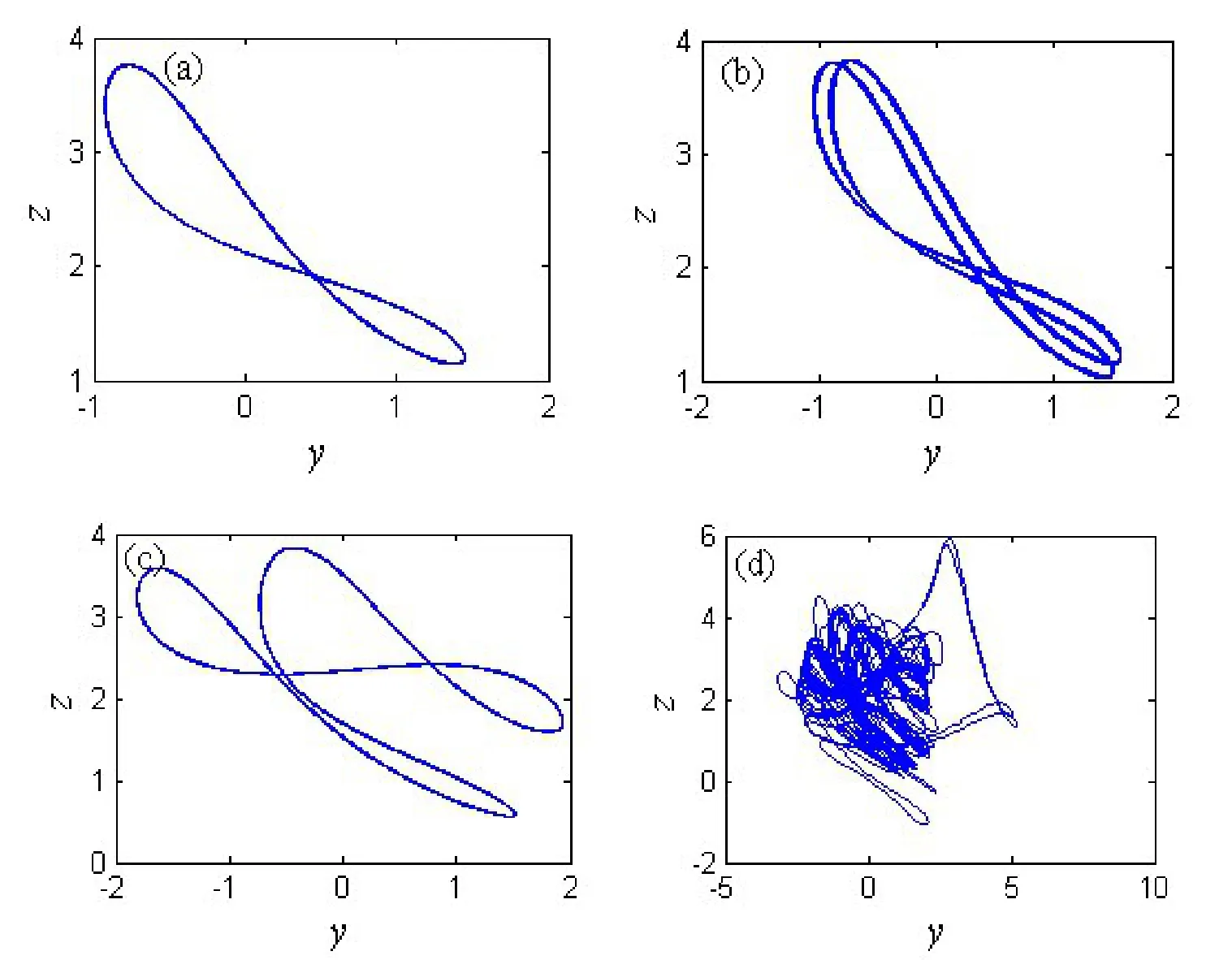
图6 电路在不同参数β时的相轨图。(a)α=-7；(b)α=-6.3；(c)α=-4.17；(d)α=-3.4

固定α=-2，使得参数β在[0.1,17]内变化时，系统的Lyapunov指数谱和状态变量x的分岔图分别如图7(a)和(b)所示。画状态变量x的分岔图选取的Poincaré截面为x=0，即系统的三维相空间中垂直于x轴的过原点的平面。此时系统的Lyapunov指数谱和Poincaré截面表现的运动轨迹的稳定和不稳定区间是一致的。从图7(a)可以看出，当参数β∈[0,3]时，系统的Lyapunov指数形式为（0，-，-），表明系统处于周期态，此时图7(b)的分岔图具有相同动力学特性，在此范围内，系统经一次短暂倍周期分岔从周期1转换为周期2，又通过反倍周期分岔进入周期1。当参数β＞3时，出现了两个正的Lyapunov指数，系统进入超混沌状态。可以看出，该并联忆阻混沌系统在很宽的参数范围内都处于混沌状态。

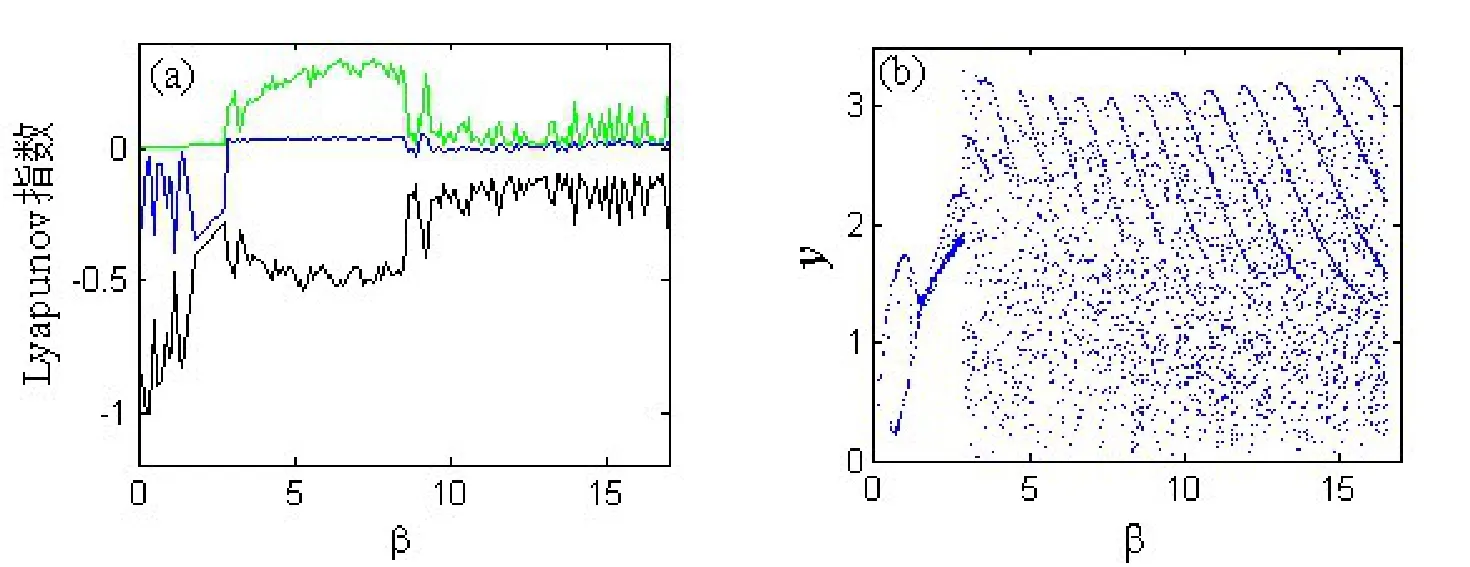
图7 电路参数β变化时Lyapunov指数和分叉图。(a)Lyapunov指数谱；(b)分岔图

3 结论

近年来研究的忆阻混沌电路基本上是用忆阻器代替蔡氏电路中的蔡氏二极管来实现的，产生的混沌吸引子与蔡氏混沌吸引子具有一定的相似性。本文采用有源压控忆阻和电容、电感并联构成了一个简单的并联忆阻混沌电路系统，建立了系统的无量纲数学模型，并采用数值仿真的方法研究了不同电路参数下该并联忆阻混沌电路的非线性动力学现象。仿真结果表明，该系统能产生一类新的折叠的超混沌吸引子，随着参数β的变化，系统具有很宽的混沌状态区域，随着参数α的变化，系统会产生瞬态混沌、混沌状态突变为周期态等丰富的动力学现象。该混沌系统电路结构简单、易于实现，同时存在复杂的超混沌吸引子，在混沌保密通信中具有一定的潜在应用价值。