基于样本差异性的多标记特征选择算法

唐 莉，王晨曦，胡敏杰，林耀进,2，郑文彬

（1.闽南师范大学计算机学院，福建漳州363000；2.数据科学与智能应用福建省高等学校重点实验室，福建漳州363000）

多标记学习是模式识别和机器学习等研究领域的热点问题。多标记学习框架中每个对象不再局限于单一类别标记，而是可能同时用多个类别标记来表征该对象的语义信息[1-3]。通常，多标记数据集的高维性会严重干扰分类学习的过程[4]。特征选择作为一种常见的降维技术，根据一定的评价准则选择一组能表征原始特征空间的过程。常见的评价准则有信息度量[5-7]、一致性度量[8]、依赖性度量[9]和大间隔[10-13]等。目前，在单标记决策系统中，利用样本的分类间隔可以有效地度量特征的重要性。然而，在多标记决策系统中，样本在不同标记下分组的不确定性导致仅用样本分类间隔很难有效地度量特征的重要性，因为目标样本在不同类标记下相应的正负类近邻样本并不固定。因此，本文设计了一种基于样本差异性的多标记特征选择算法。

1 大间隔

给定单标记决策系统NDT=＜U,F,C＞，其中U={x1,x2,…,xn}是样本集，F={f1,f2,…,fn}是一组用来表述样本的属性集合，C代表类别标记。

定义1[14]U是一个非空的样本集合空间，若∀x1,x2,…,xn∈U有且仅有一个确定实函数Δ与之对应，且Δ满足：(1)Δ(xi,xj)≥ 0当且仅当xi=xj,Δ(xi,xj)=0；(2)Δ(xi,xj)= Δ(xj,xi)；(3)Δ(xi,xj)≤ Δ(xj,xi)，则称＜U,Δ＞是度量空间。其中，Δ是用来度量样本空间U上距离的函数。在m维空间中，任意两点xi=(xi1,xi2,…,xin)和xj=(xj1,xj2,…,xjn)间的距离定义为闵科夫斯基距离：

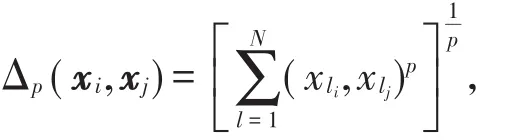
当P=1时，Δ函数表示曼哈顿距离；当P=2时，Δ为欧式距离；当P→∞，Δp(xi,xj)=|xli,xlj|。

定义2[15]样本空间用U来表示，x表示样本，则x的分类间隔为

其中，NH(x)和NM(x)分别表示在样本空间U中距离x最近的具有相同类别标记的样本和不同类别标记样本。Δ[x ,NM(x)]和Δ[x ,NH(x)]分别表示样本点x到NM(x)和NH(x)的距离，见图1。

RELIEF算法主要运用大间隔方法度量特征对样本是否可分，即

其中，‖xi- NM(xi)‖-‖xi-NH(xi)‖表示样本在第i个特征分量上间隔的2倍。

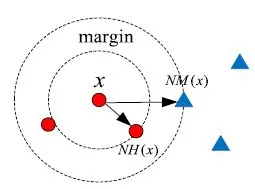
图1 样本x的分类间隔margin(x)

2 基于样本差异性的多标记特征选择算法

2.1 采样

在多标记学习中，Zhang等指出样本是否具有某个标记受其类属属性决定[16]。另外，样本之间标记的关联性说明了多标记数据集特征并非所有样本都具有同等重要性。因此，本节利用聚类技术对多标记数据集进行采样，以组成新的多标记决策系统。具体来说，给定多标记数据集D={(xi,li)|1≤i≤n}，特征向量(xi1,xi2,…,xid)T构成了d维样本xi，其中，样本xi∈L的所具有的标记的集合用lk表示。对于标记lk∈L，具有类别标记的样本和不具有类别标记的样本构成的集合[16]可表示为

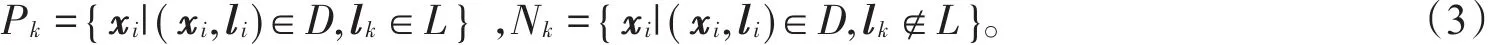
为了有效表征数据和分析样本的内在性质，采用k-means对正负类样本进行聚类，将集合Pk的个聚类中心记为{,,…,}，集合Nk的个聚类中心记为{,,…,}。文献[16]提出，对于可能存在正负类的样本个数不均衡情况，将Pk和Nk的聚类个数置为等同，即mk==，即样本集合在Pk和Nk上的聚类个数可设定为

其中，|·|表示返回集合的势，r=[0,1]是限定聚类样本的个数。

通过（3）式与（4）式，多标记数据集D可转换为由具有代表性的样本组成的多标记决策系统＜U,F,L＞，其中U={x1,x2,…,xn}表示样本集，F={f1,f2,…,fm}是用于描述样本的一组特征，L={l1,l2,…,lt}是一组标记集合。

2.2 样本差异性

根据（2）式可以度量单标记决策系统中每个特征与标记之间的相关性，权重越大说明特征越能区分样本的类别。在多标记数据集中，样本在标记空间中的关系并不确定，即在某个标记下为同类，但在另一个标记下却为异类。因此，在多标记决策系统中仅从样本间隔来度量特征的重要性具有一定局限性。

定义3给定多标记决策系统＜U,F,L＞，对于∀l∈L，则样本x在特征f下的分类间隔为

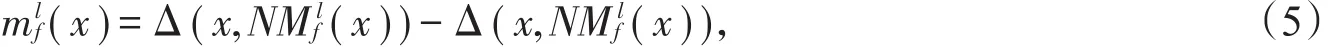
根据RELIEF算法的思想，特征的权重可通过样本的分类间隔进行度量。通常特征对样本的可分性越强，分类间隔会越大；否则，越小。当mlf(x)＞0时，表示对于标记l，样本x到最近异类样本的距离大于到最近同类样本的距离，此时特征对样本x是可分的；反之则表示特征对样本x不可分。为了便于计算，将mlf(x)＜0设置为ml(x)=0。

定义4对于整个标记空间L，样本x在特征f下的分类间隔定义为

定义4反映了样本在多标记决策系统中某个特征空间下的分类间隔度量特征对样本的区分能力。

定义5给定多标记决策系统＜U,F,L＞，特征f∈F在样本空间的分类间隔为(x)，则特征f在样本空间中间隔大于零的样本构成的集合为={xi|(xi)＞0,xi∈U}，那么，分类间隔大于零的样本数目为||。

定义6给定多标记决策系统＜U,F,L＞，对于∀x∈U，在特征f下，若(x)＞0且||＞0，则说明样本x是有差异性的样本。

定义7∀x∈U,w为特征的权重向量，则特征子集的评价函数：

定义8样本x在特征f下的分类间隔度量特征的权重计算公式为

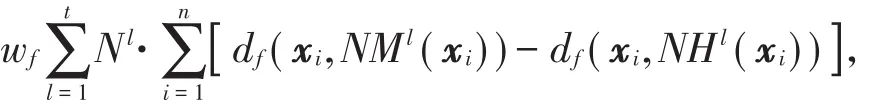
其中，df(xi,NMl(xi))代表在特征f和类标签l下，距离样本xi最近且具有不同类标签的样本，df(xi,NHl(xi))代表具有相同类标签的样本的距离。本文将距离df(x,y)定义为

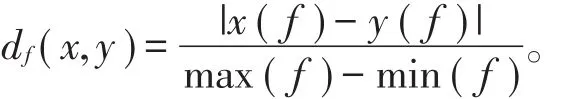
基于样本差异性，由（6）式设计一种类似RELIEF的多标记特征选择算法（MFSD），具体描述如下：

输入：多标记数据集D

输出：特征子集lable_featurespace

①根据（3）式与（4）式，获得由具有代表性样本组成的多标记决策系统＜U,F,L＞；

②for eachf∈F；

③根据（6）式计算每个特征的权重；

④end；

⑤按特征权重大小把排序好的特征值放在lable_featurespace。

3 实验设计

为了证明本文算法的有效性，实验取MDDMspc[17]、MDDMproj[17]、RF_ML[11]、MLNB[18]和 FWLW[19]作为对比算法。用ML-KNN[20]的分类算法来对已经进行特征选择后形成的新的数据集进行评价，其中ML-KNN设定为默认参数值，平滑参数s=1，近邻k=10。

3.1 实验数据

本文实验从Mula(http：//mulan.sourceforge.net/datasets.Html)中选取了4个多标记数据集，表1刻画了数据相关信息。

表1 数据集的基本信息

3.2 评价指标

实验采用平均查准率（Average Precision，AP）、排序损失（Ranking Loss，RL）、汉明损失（Hamming Loss，HL）、覆盖率（Coverage，CV）4个评价指标[17-18]验证算法的有效性。令测试集：

Z={(xi,Yi)}⊂Rd×{+1,-1}L，根据预测函数fl(x)可定义排序函数为rankf(x,l)∈{1,2,…,L}。

实验所用评价指标中，AP的值越高说明分类性能越优，最优为1；而RL、HL和CV等3种指标值越小说明分类性能越优，最优值为0。

3.3 实验结果与分析

下面从两个方面来验证MFSD算法的有效性：第一，与已经提出的算法在特征子集的个数以及分类性能两方面作比较；第二，观察特征子集的数目与分类性能之间的关系。本文采用的对比算法为MDDMspc、MDDMproj、RF_ML和FWLW，且对比算法均得到一组特征排序，本文将选择排序前k个特征作为最终的特征，并将k设置为与MLNB最终选择特征相同的数目。表2给出了各算法在不同评价指标下的实验结果。表中Original列的数值表示未做选择的特征的分类性能；数值后的符号“↑”表示分类性能与数值的大小成正比；符号“↓”表示二者成反比；数值后的符号“√”在相应指标下该算法诱发的分类性能优于初始特征；斜体表示各算法与相应的指标下的分类性能平均值，加粗表示所有值中的最优。

根据表2的实验结果可发现：

（1）表2分别统计了MDDMspc、MDDMproj、RF_ML、MLNB、MFSD和FWLW算法在4个数据集、4个评价指标上的16个结果。与各算法进行对比，结果显示本文提出的算法具有更好的性能。

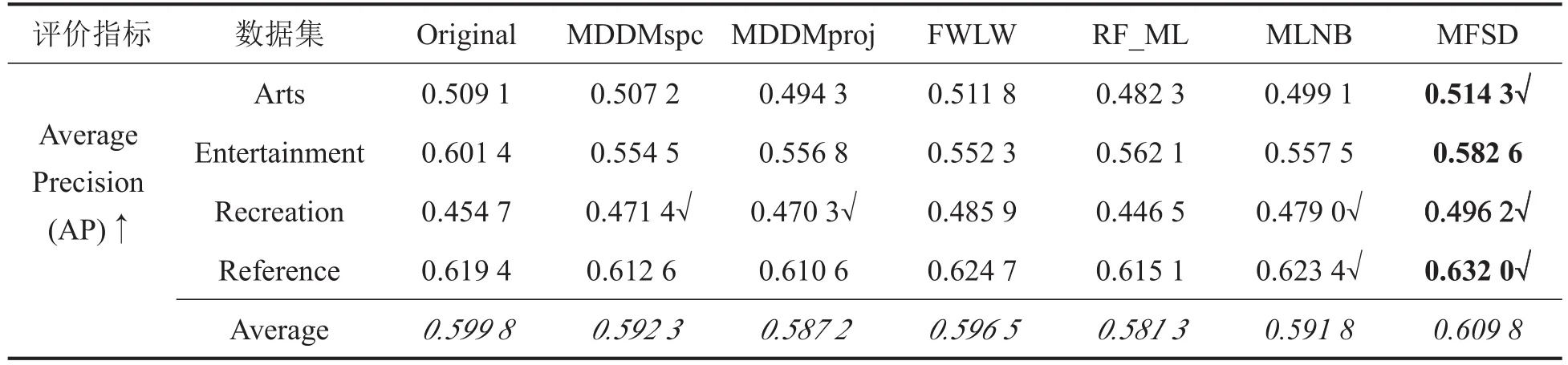
表2 各对比算法不同指标下的分类性能

续表2

（2）从平均分类精度上来看，MFSD在4种评价准则中获得的平均分类性能极其明显地优于其他5种对比算法和原始分类性能，这更加充分地说明了本文算法的有效性。

为了更直观地看出特征子集的个数与分类性能之间的关系，图2～5分别表示在AP、HL、RL和CV这4种评价指标下，各算法的分类性能的变化趋势。可以发现，本文所提的MFSD算法优于其他的算法。

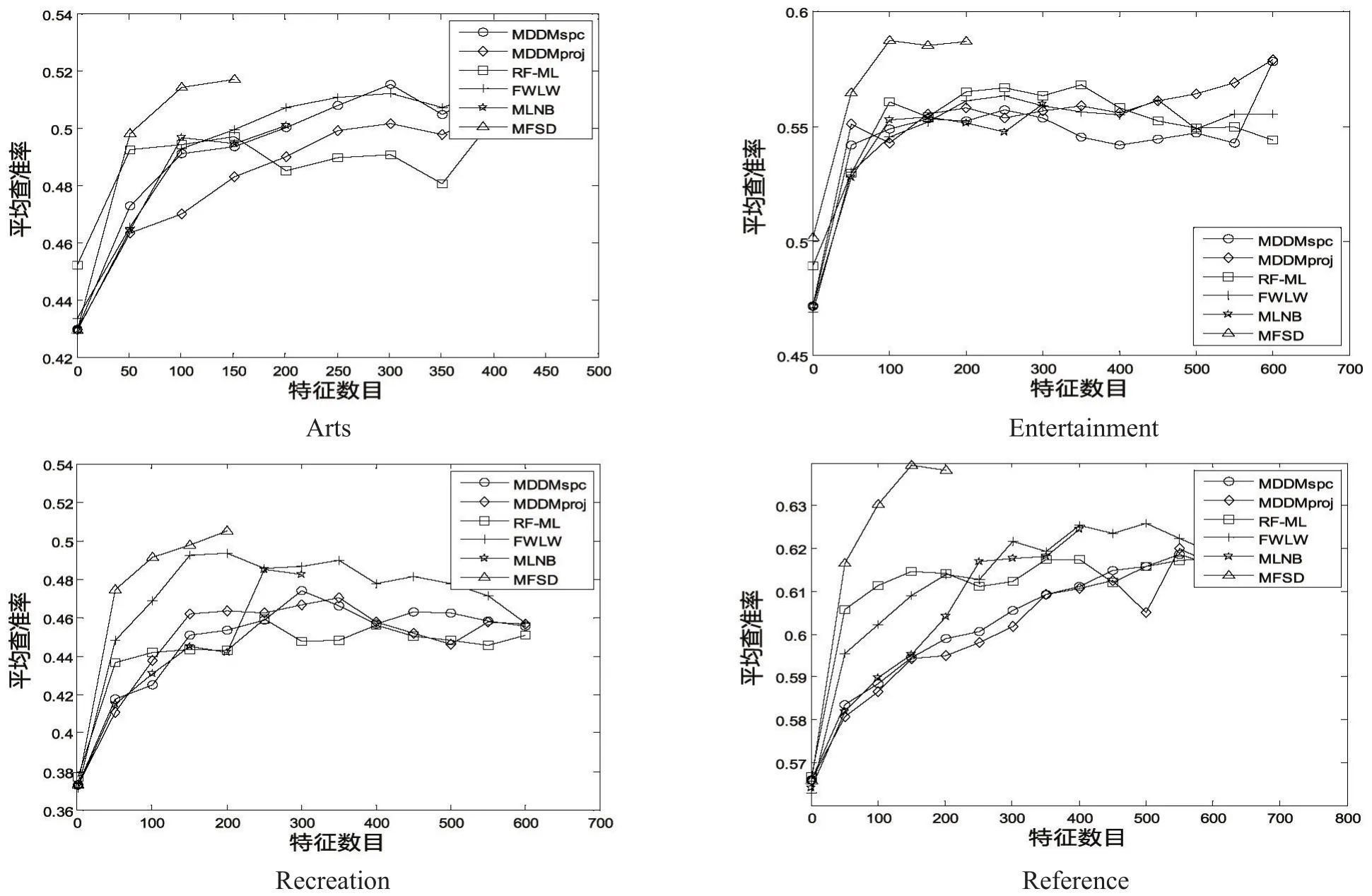
图2 特征数目与AP的关系图

图3 特征数目与HL的关系图

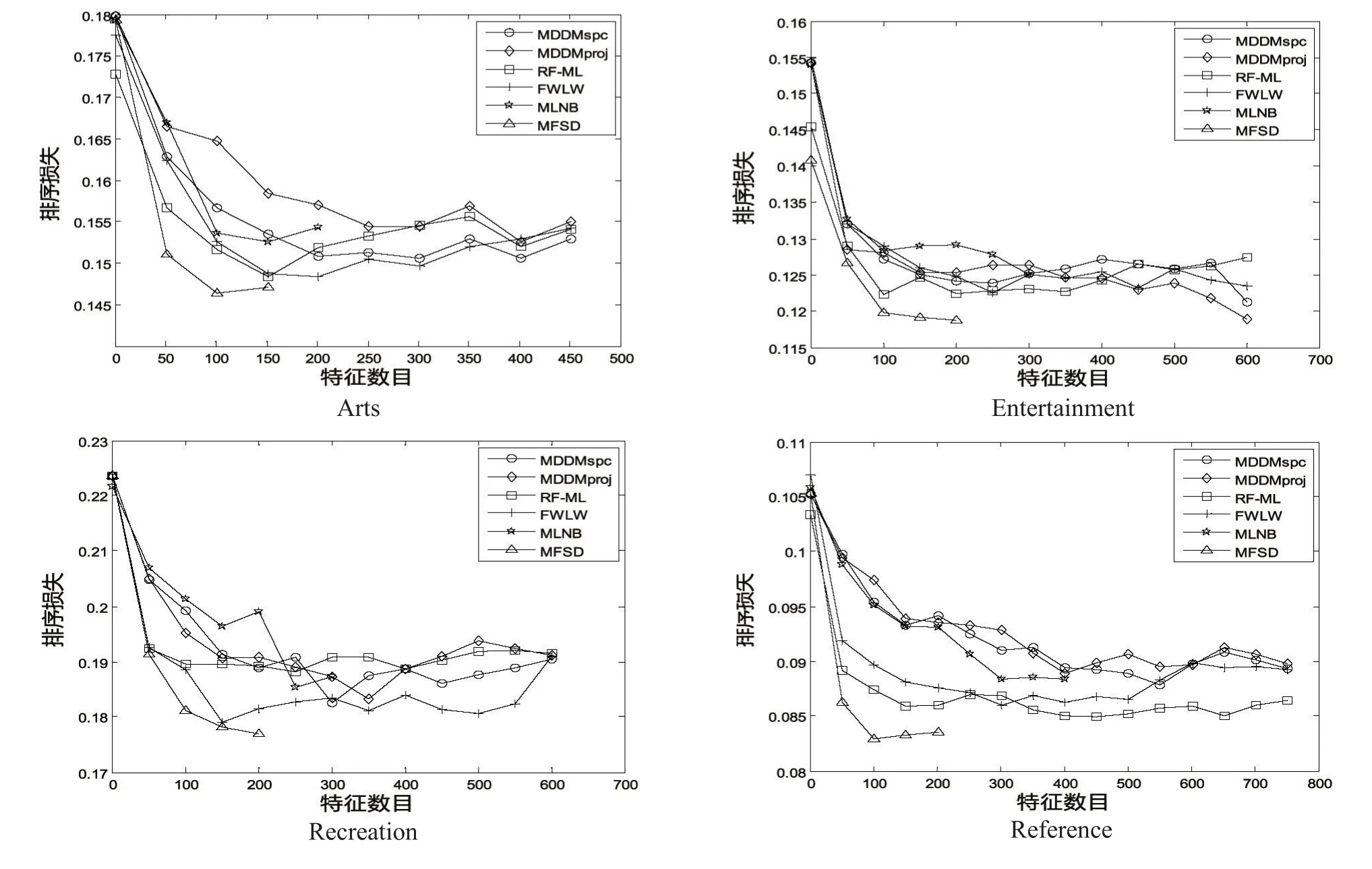
图4 特征数目与RL的关系图

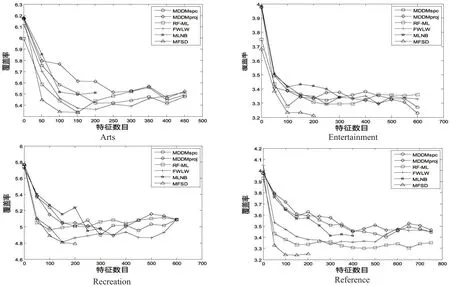
图5 特征数目与CV的关系图

4 总结

本文提出了一种类似RELIEF基于样本差异性的多标记特征选择算法，在每个标记下反复计算特征空间中所有样本的间隔，充分考虑了样本的差异性对特征权重学习的影响。从样本的分类间隔及样本分类间隔数量出发定义了样本的差异性，基于此，设计了一种前向启发式的基于样本差异性的多标记特征选择算法。本文所提出的算法与对比算法用了相同的数据集以及评级指标，实验显示MFSD算法分类性能会更优。