PT对称结构同相和反相放大调制器的仿真研究

方云团，李小雪

（江苏大学计算机科学与通信工程学院，江苏镇江212013）

由于光调制器和光放大器在光通信中的重要地位，人们对于如何高效地进行光调制和光放大的研究也越来越多。宇称—时间（Parity-Time：PT）对称这一概念来源于量子力学，PT对称的光学波导体系具有独特的光学性质，在光子信息处理以及集成光学方面具有重要的应用价值[1-15]。与普通结构相比，PT对称系统中会出现许多奇异现象，例如多种类型的PT对称光孤子、光能量振荡现象、非互易性的光传输[2]、双重折射、损耗引起的透射效应[3]、完美吸收体[4-6]、光隔离[7-10]，等等。对于PT对称的结构，本课题组也做了相关的研究[12-16]。目前，一般的PT对称结构都具有较高的反射率，其透射率却不能满足要求。因此，如何利用具有缺陷模式的PT对称结构的优点来实现较高透射率，从而实现电信号到光信号的高速调制和高效放大是目前所要解决的问题。大规模集成以及体积小型化是未来电路及器件发展的趋势，而将电光调制器和光放大器集于一个设备，将对未来电路的集成、设备小型化具有重要的意义。本文将设计一个基于PT结构的放大器，该器件在实现正相放大的同时，也具有反相放大的功能。

1 结构模型

图1所示为电光调制器模型原理图。该模型具有周期性的PT对称结构，它的周期结构由损耗介质层A和增益介质层C组成，整个结构可以表示为(ABC)ND(CBA)N。在这个结构中，D层是缺陷层，N是周期数。为了实现调制器的功能，把B层和D层设置为一种电光材料板，外加电场沿着z轴。这种电光材料板是一种具有电光效应的光学功能材料，在外加电场作用下，材料的折射率将发生变化。不失一般性，在这里，B层和D层材料选为LiTaO3。A层和C层材料的介电常数可以用洛伦兹模型来描述，在外界泵浦的作用下，材料可实现增益或吸收，见参考文献[17]。模型中所使用的材料都是非磁性的。

正向入射波和反向入射波分别表示沿着+x和-x方向传播的波。对于自由空间中的这样一个分层结构，透射率T和反射率R可以通过传输矩阵来计算。LiTaO3的折射率依赖于外部电场。因为E的方向沿着z轴，所以折射率椭球方程为

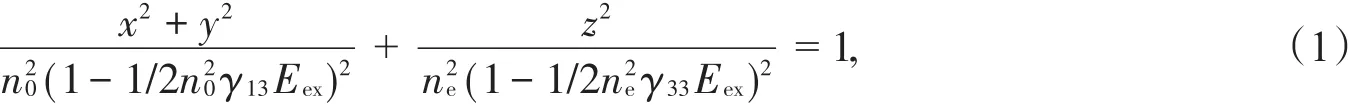
其中，x，y，z是椭球面上点的坐标，n0、ne分别是o光和e光折射率，γ13和γ33是电光张量，Eex是外加电场幅度。

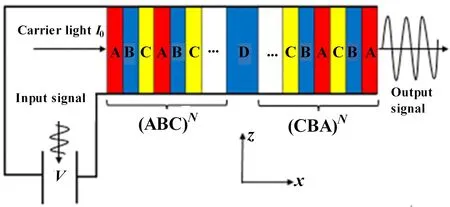
图1 设计的电光调制器的原理图

由于入射波是TE波，电场沿着y轴，B层的折射率可以写成：

在这个公式中，nB0=2.176，电光系数γ13=8.4×10-12m/V。A层和C层由洛伦兹模型定量描述为

式中，ω0是共振频率，ω0=2.9×1015s-1；γ是阻尼常数，γ=2.5×1014s-1；A为宏观洛伦兹振荡强度，|A|=2.155×10-4，它描述了系统中的增益与量子点的浓度及激发态的量子点的分布有关[17]，A＞0对应于损耗，A＜0对应于增益。A层和C层分别是损耗材料和增益材料，它们的介电常数均满足实部偶对称、虚部奇对称，这样才满足PT对称的条件。所有层的厚度（d）都是精心选择以满足共振的条件，这里，dA=dC=422 nm，dB=392 nm和dD=4 dB。这样的结构会在λ0=633 nm处出现缺陷模式。

2 结果与分析

选取周期N=6，外加电场Eex=0，在(2)式和(3)式所表述的参数条件下，即结构参数：nB=2.176，|A|=2.155×10-4，ω0=2.9×1015s-1，应用传输矩阵法[16]计算其透射谱，如图2所示。从图2中可以看出，从615 nm到650 nm的带隙中，在633 nm处有一个非常清晰的传输峰值，这个峰值对应于缺陷模式。不同于一般周期结构的常规缺陷模式，它的峰值为11.38，大于1。这就说明了波长为633 nm的光不仅可以通过该结构，而且还被放大。

以上结果表明，该结构因为满足PT对称的条件，所以在波长为633 nm处的光被放大。它的放大机理是因为整体的结构满足耦合共振，微腔的这种效应将外界提供的能量转换为电磁能。因为在波长633 nm处有一个比较高的透射率，所以我们给定波长为633 nm的光作为入射波。共振效应与结构参数有关，结构参数的改变会影响共振效应。现通过改变nB来研究透射率的变化。其他结构参数不变，将nB做很小的改变，如图3所示（透射率取了10 lg（T），故用dB作单位），nB变化0.000 1，透射峰的峰值改变很大，但峰位仍是633 nm。由电光效应原理知，当电场加在这个结构上时，nB的变化会引起透射峰峰值的变化。这样的结果为我们提供了设计电光调制器的思路。

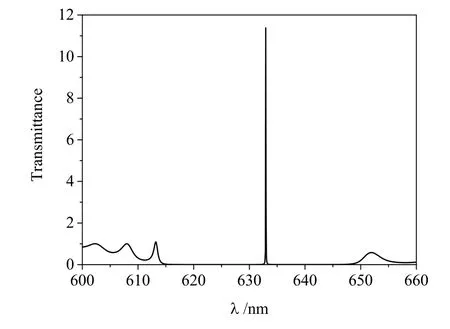
图2 电光调制器结构模型透射谱

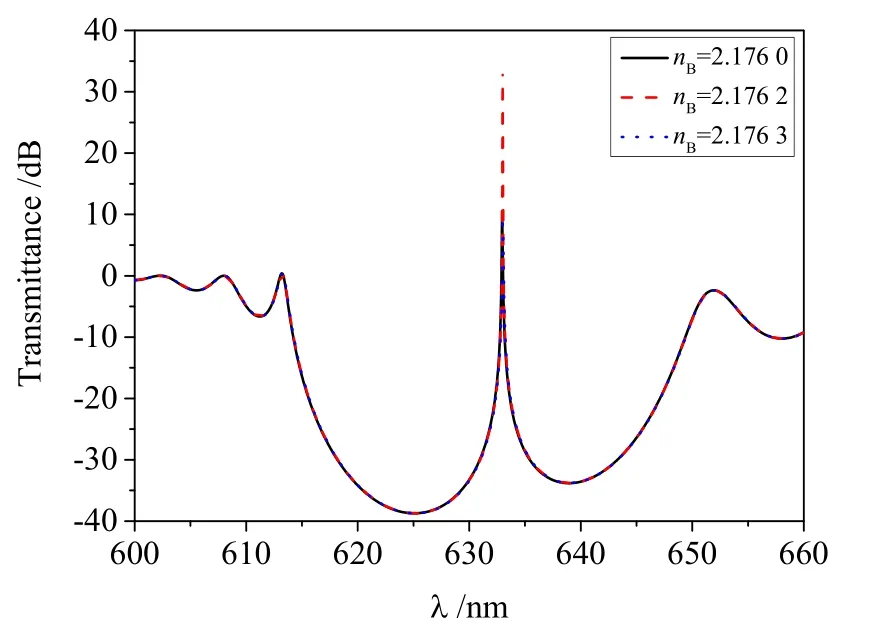
图3 折射率不同时电光调制器结构模型的透射谱

根据设计的结构模型，固定波长为633 nm，计算nB不同时其透射率，结果如图4所示。从图4可以看出，曲线是中心对称图形。在对称轴左侧，曲线的斜率为正，可实现同相放大调制；在对称轴右侧，曲线斜率为负，可实现反相放大调制。先讨论同相放大调制的情况。在标注的阴影区域内是选择的线性范围，在此线性范围内的调制属于线性调制。这个线性范围的中点叫静态工作点，即图4中阴影处曲线的黑点。为了实现nB在这个线性范围内变化，我们在一个交变电场E(t)的基础上，加一个静态偏置电场Eb，此时nB的大小由下式决定：

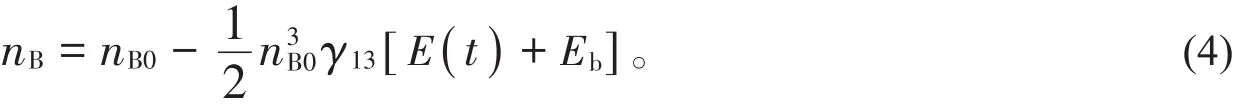
(4)式中的Eb决定了nB变化范围的中心，由静态工作点的位置算出Eb的大小，从而对外电场进行设置。通过观测，图4(a)静态工作点的位置为nB=2.176 17，图4(b)表示nB在静态工作点附近随着时间的变化。因为U(t)和E(t)的线性关系，E(t)电场的变化就表示电压U(t)信号。根据(4)式，要得到nB=2.176 17，令外加电场E(t)=0，算得Eb=-4.1×106V/m。 PT 对

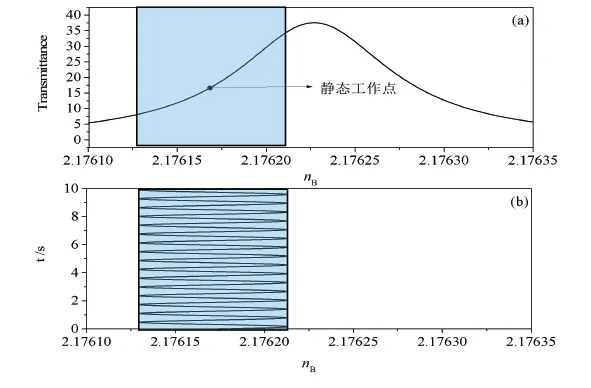
图4 正相静态工作点的选取和线性范围。（a）透射率随nB的变化；(b）在静态工作点附近因为电场的调制，nB随着时间的变化曲线

作为一个例子，设置输入信号E(t)=1×106×sin(t×10)V/m，偏置电场Eb=-4.1×106V/m，输入与输出信号分别如图5(a)、5(b)所示。由图5可以看出，输出信号和输入信号是同相且同频变化。另外，从图5明显可以看出，输出信号的幅度要大于输入信号幅度，这说明输出信号被放大了。由此可见，我们设计的这种结构同时兼有调制器和放大器的功能。

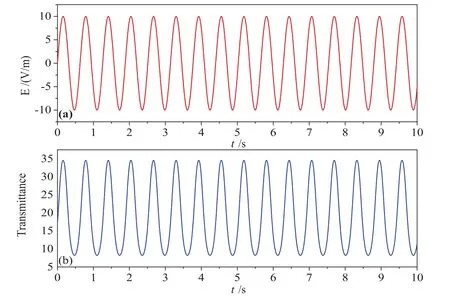
图5 (a)输入信号，(b)输出信号输入信号：E(t)=1×106×sin(t×10)V/m，Transmittance表示输出信号，E表示输入信号

接下来，将线性范围取在对称轴的右侧，如图6(a)所示，这时所实现的功能是反相调制。图6（b）nB一样表示在静态工作点附近随着时间的变化。图7所示为输入信号与输出信号图，由图可知，信号被反相调制的同时也被放大。

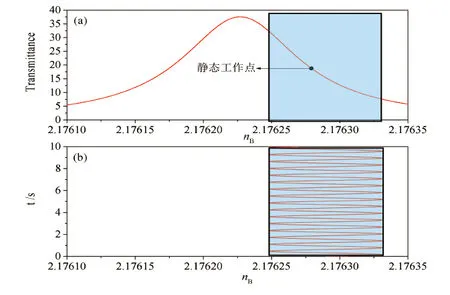
图6 反相静态工作点的选取和线性范围。（a）透射率随nB的变化；(b）在静态工作点附近因为电场的调制，nB随着时间的变化曲线。静态工作点nB=2.176 29,Eb=0.694 71×107V/m，输入信号为E（t）=1×106×sin(t×10)V/m，Transmittance为输出信号，t表示时间

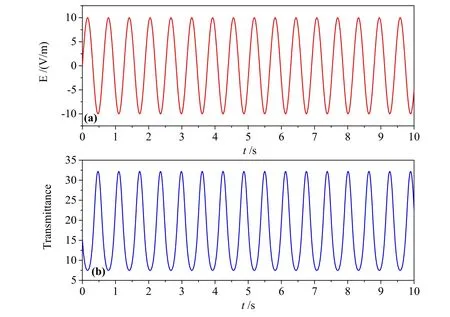
图7 (a)输入信号，(b)输出信号。静态工作点nB=2.176 29,Eb=0.694 71×107V/m，输入信号为E（t）=1×106×sin(t×10)V/m，Transmittance为输出信号,E为输入信号

3 同相放大和反相放大的一个应用设想

根据上述研究，综合考虑该结构所具有的电光调制同相放大和反相放大的功能，提出如图8所示的反相对称光调制放大器消除噪声的设计思路。

假设信号源产生的电模拟信号为s(t)，这一信号分别经过左右两路的电光调制器。根据模型图8，信号经过左支路正相放大的电光调制器后，输出信号为ms(t)，其中，m表示信号经过上支路电光调制器被放大的倍数；经过右支路反相放大的电光调制器后，输出信号为-m1s(t)，m1表示信号经过下支路电光调制器被放大的倍数。这两路信号在信道中并行传输。信号在传输过程中受到环境噪声的影响，设噪声为n(t)。输入减法器前端上支路和下支路的信号分别为m′s(t)+n(t)和-m1′s(t)+n(t)，m′和-m1′表示经过信道后由于衰减发生变化后的信号放大倍数，这样经过减法器后，输出信号为o(t)。它们的关系可以表示如下：

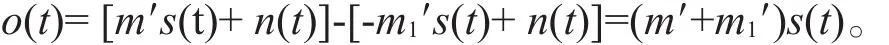
因此，借助调制器的正向放大和反相放大及减法器的共同作用，信号的白噪声得到很好的抑制。

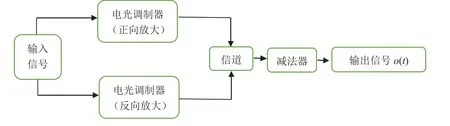
图8 实现减噪的反相对称光调制放大器理论模型

4 总结

本次的设计是基于PT对称结构同相和反相放大调制器的设计。这种结构不仅具有较高的反射率，而且满足我们对高透射率的要求。它集光调制器和光放大器于一体，在对光进行调制的同时还被放大。此结构也具有正相调制和反向调制的功能，利用此功能，还可以设计出消除白噪声的信号处理模型。