受扰非线性过程的设备退化建模与寿命预测

李健东,陈秀荣,李 娟,杨 雪,佟春明

(1.青岛农业大学机电工程学院，山东 青岛 266109；2.青岛农业大学理学与信息科学学院，山东 青岛 266109)

0 引言

设备在运行过程中不可避免地会发生性能退化，而外部环境的干扰会进一步加速设备性能退化，最终导致设备失效。目前，设备的非线性退化是寿命预测领域研究的热点。文献[1]建立了符合非线性Wiener过程描述的设备退化模型，有效解决了非线性退化过程的动态特性难以被原有线性模型描述的问题。文献[2]提出了在扩散过程的基础上对非线性退化过程进行建模，建立了新的非线性损伤演化方程，并在线预测了设备的剩余有效寿命。为了对非线性多退化系统进行有效的剩余寿命预测，文献[3]～文献[4]提出了将非线性加速退化模型与失效率模型相结合的寿命预测方法，并将贝叶斯方法融入寿命评估中。文献[5]则利用卡尔曼滤波和期望最大化算法的迭代估计方法，以改进剩余寿命预测精度。根据设备性能退化非线性的特点，利用分段建立性能退化模型的方法[6]，将贝叶斯更新与Copula理论结合到模型中[7]，有效提高了对设备性能退化过程描述的准确性。在产品退化过程的随机效应分析基础上[8]，提出了测量含不确定性情况下的非线性随机退化建模方法[9]。

以上研究和其他一些研究通常将外部干扰视为突发因素而忽略，很少将其作为退化建模中一个独立的因素[10]。文献[11]将非线性退化过程转换为线性退化过程，再通过维纳过程进行退化建模。文献[12]提出采用状态驻留信息模型的方法，对行程开关的剩余使用寿命进行预测。然而，目前还没有看到受到Poisson分布干扰的双参数非线性退化过程的建模和寿命预测研究成果。

为此，本文在双参数的贝叶斯更新模型中考虑服从Poisson分布的外部环境干扰的影响，从而提出了新的设备性能退化模型并进行寿命预测。

1 外部干扰下的设备非线性退化建模

为了对设备的退化过程进行建模，现作如下描述：A(t1),A(t2),…,A(tn)表示在时刻t1,t2,…,tn可以观测到的设备监测数据；A(ti)表示在时刻ti的观测值。考虑设备退化的非线性模型[13]为：

(1)

式中：φ为固定参数变量；θ和β为随机变量；ε(ti)为随机误差。

对式(1)进行对数变换，可得：

(2)

式中：lnφ为初始退化量；lnθ为随机变量。

L(ti)=lnφ+η+βti+ε(ti)

式中：η为随机变量。

在设备运行的过程中，由于所处的环境复杂多变，受到外部环境干扰因素的影响是随机的。因此，干扰发生的次数N(t)可由强度为λ的泊松随机过程来表示。则时刻t，发生n次干扰的概率为：

式中：n为外部环境干扰的次数，根据泊松分布表计算。

Q1,Q2,…,Qk为设备在t1,t2,…,tk时刻对应的退化量。该退化量为随机变量，其分布通常是根据分析实验数据获取的样本得到。本文假设设备的退化量服从正态分布，即Qj～N(μ,σ2)。

为了考虑外部干扰对退化过程的影响，本文提出考虑外部环境干扰影响的退化模型为：

(3)

2 参数估计与剩余寿命预测

针对模型(3)，参数估计的步骤如下。

①确定先验分布。

②确认后验分布。

根据贝叶斯估计的性质，选取共轭先验分布，所以后验分布也服从正态分布：

p(η,β|Lj)∝f(Lj|η,β)π(η,β)

在t1,t2,…,tk时刻，观测数据为Lj=l1,l2,…,lk，相应联合概率密度函数为：

进而得到(η,β)的后验分布：

取λ=1，则：

根据贝叶斯定理，可得到各个参数的估计：

(4)

(5)

③运用极大似然估计的方法对参数进行估计。

(6)

对式(6)取对数，得对数似然函数为:

(7)

分别对式(7)中的η和β求偏导，并令导数为零，得到似然方程：

(8)

对式(8)进行计算，得到：

(9)

④剩余寿命的密度函数。

通过建立模型与求解过程，得到设备剩余寿命分布函数为：

式中：tk+T为设备到达阈值的时刻；tk为当前测量时刻；T为设备的剩余寿命。

注意到时间tk的设备剩余寿命T满足L(T+tk)=D，则：FT|L1,…,Lk(t)=P{T≤t|l1,l2，…,lk}条件下，T的条件累积分布函数(cumulative distribution function，CDF)[13]为：

P{T≤t|l1,l2,…,lk}=P{L(t+tk)|l1,l2,…,lk}=1-P{L(t+tk)≤D|l1,l2,…,lk}

式中：Z为标准的正态随机变量；Φ(·)为标准正态随机变量的CDF。

事实上，找到在(t+tk)时的信号值大于D的概率，就已经确定了剩余寿命的条件累积分布函数。即T的截断的条件累积分布函数为：

由T的截断累积分布函数，可以导出截断的条件概率密度函数：

(10)

式中：φ(·)为标准正态随机变量的条件概率密度函数。

3 仿真研究

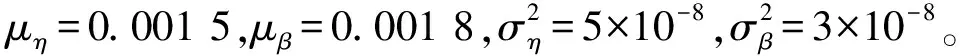
图1 剩余寿命概率密度函数曲线

图2 可靠度曲线

图1、图2中：f1和z1为不考虑外部环境干扰的情况；f2和z2为考虑外部环境干扰的情况，即采用本文方法得到的曲线；f3和z3为真实情况。

由图1和图2可以看出，考虑干扰时的概率密度函数曲线和可靠度曲线更接接近真实情况。换言之，本文提出的考虑外部干扰的退化建模可以提高剩余寿命的预测精度，从而保证设备及时得以检修和维护，以达到降低风险、减少人员伤亡和经济损失的目的。

已获得的6个同类型的防喷阀寿命数据(单位：kh)为[14]：33.83、36.65、45.57、36.6、42.12、39.03。该类防喷阀的平均寿命为Tave=3.8×104h。为了比较模型预测的剩余寿命的分布，给定tk∈(0.3Tave,0.5Tave,0.9Tave)为基准时间，得到预测的平均剩余寿命对比如表1所示。从表1中可以看到，与不考虑外部环境干扰的方法相比，本文考虑外部环境干扰的剩余寿命预测更接近真实值。

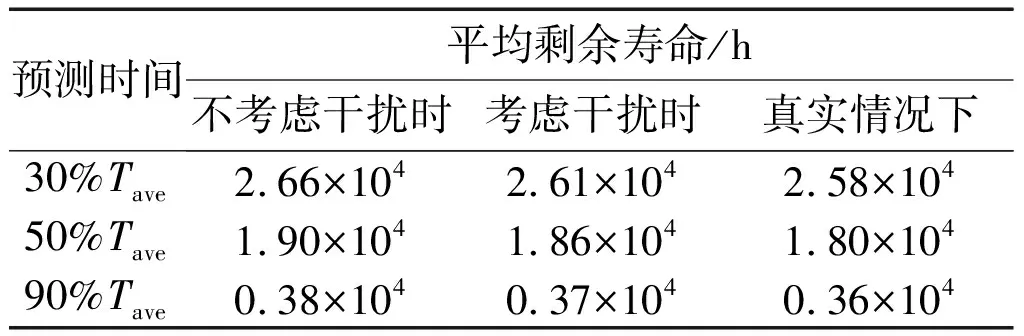
表1 平均剩余寿命对比

4 结束语

本文考虑了服从Poisson的外部环境干扰对设备性能退化的影响，建立了非线性的性能退化模型。采用贝叶斯方法与极大似然估计方法估计分布的参数值，得到设备的剩余寿命的概率密度函数及相关分布，从而更加准确地描述了设备的性能退化过程的动态性。下一步工作考虑测量误差对设备的剩余寿命预测的影响，从而更好地对设备的剩余寿命进行预测。