基于改进的自适应渐消UKF机床主轴热平衡试验
2019-04-28余文利邓小雷姚鑫骅傅建中
余文利 邓小雷 姚鑫骅 傅建中
(1.衢州职业技术学院机电工程学院, 衢州 324000; 2.浙江大学浙江省三维打印工艺与装备重点实验室, 杭州 310027;3.浙江永力达数控科技股份有限公司, 衢州 324000)
0 引言
对于精密数控机床而言,几何误差、刀具磨损等都会影响加工精度,但是主轴系统高速旋转导致主轴轴承处产生较多热量,引起主轴热伸长对机床的加工精度影响较大[1]。大量研究表明,精密加工机械的最大的误差源是机床外部环境和内部热源引起的热误差,占总体几何误差的40%~70%[2]。主轴是机床的核心部件,其性能对机床的切削速度和加工精度至关重要[3]。在减少热变形或进行热误差补偿之前,需获得机床主轴的热态特性,如温度场分布、热传导特性、温升特性、降温特性、热平衡时间以及热位移和热应力场分布等。
对机床热态特性进行建模的方法主要有有限元法、热网络法和有限差分法等,其中有限元法[4-7]最常用。利用有限元模拟方法可以得到主轴温度场和温度关键点,然而,由于主轴结构复杂,仿真模型无法接近实际工况,导致温度的模拟结果不能反映真实的温度变化。因此,获得机床主轴热态特性的最主要方法仍是主轴热平衡试验。数控机床从启动到达到热平衡状态是一个缓慢变化过程,机床主轴热平衡试验周期长,一般根据机床的品种、类型和规格的不同,试验时间可从数小时到数十小时不等。因此,研究快速识别主轴温升特性的方法,缩短数控机床主轴热平衡试验时间,对提高数控机床热态特性分析效率具有重要意义。为提高机床热平衡试验的效率,国内外许多学者提出了机床温升快速辨识方法,通过使用热平衡试验周期中一小段时间的温度测量值来预测机床结构的原始温升,取得了一些研究成果[8-10]。
无迹卡尔曼滤波(UKF)算法因其在处理非线性状态估计和参数识别方面的明显优势而得到广泛应用[11]。为了准确地估计压电堆叠作动器的非线性滞后和蠕变效应,MINASE等[12]提出了一种基于UKF算法的自适应识别方法。WANG等[13]探索使用UKF算法估计电动车电池的峰值功率。UKF算法也成功地应用于各种环境温度下基于开路电压估计锂电池充电状态[14]。REGULSKI等[15]使用UKF算法估计功率分量和频率。在移动机器人同步定位和映射领域,UKF算法用于地标位置估计和更新[16]。虽然UKF算法已经成功应用于实时非线性结构系统辨识,但是标准UKF算法存在性能下降甚至发散等问题,而且研究发现其先验噪声分布与真实系统中的分布存在不匹配现象[17]。为了克服标准UKF算法的不足,阮承治等[18]利用免疫粒子群算法来优化UKF算法,提出一种组合导航定位方法。HU等[19]提出两种不同的UKF算法用于GPS车辆导航,一种基于渐消记忆,另一种基于方差估计。LOEBIS等[20]使用模糊逻辑技术来更新传感器的噪声协方差。孙宇新等[21]提出一种改进的UKF算法,并且使用该算法实现了无轴承异步电机的转速估计。
本文提出基于改进的自适应渐消卡尔曼滤波(AFUKF)快速辨识机床主轴温升的方法。通过利用残差序列的协方差,自适应地改变渐消因子以调整测量值,有助于减小先前测量值和不准确的系统模型对预测精度的影响,可直接应用于测量数据进行辨识,在此基础上引入自适应规则动态调整过程噪声和测量噪声协方差,以提高UKF算法的滤波性能。
1 基于改进的AFUKF算法的机床主轴温升快速辨识
1.1 渐消UKF算法基本原理
非线性离散模型如下
(1)
式中xk——k时刻n1阶系统状态向量
yk——k时刻m1阶测量向量
f(·)、h(·)——非线性函数
wk——过程噪声,满足高斯分布wk~N(0,Qk)
Qk——过程噪声协方差
vk——测量噪声,满足高斯分布vk~N(0,Rk)
Rk——测量噪声协方差
渐消UKF算法具体步骤如下:
(1)初始化
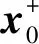
(2)
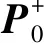
(2)时间更新
通过无迹变换构造2n+1个采样点,即sigma点集
(3)
新构造采样点的对应权值为
(4)

i——采样点序号
δ——缩放比例参数
κ——待选参数
φ——调整参数
η——高阶误差采样因子,满足高斯分布时取为2
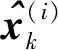
(5)

(6)
(7)

(3)测量更新
对上述预测值进行无迹变换,构造2n+1个新Sigma点集
(8)
(9)
(10)


(11)
Kalman滤波增益阵为
(12)
式中αk——渐消因子
系统的状态与协方差更新为
(13)
式中yk——在kΔt时刻的实际测量向量
Δt——采样间隔
假定测量持续进行了NΔt时间,N为采样总次数,则在时刻0, Δt,…,NΔt分别有N+1个测量值。即可以利用在NΔt时间段内的实际测量值更新状态变量的后验均值和协方差估计。本文将NΔt定义为辨识时间,在辨识时间内,测量更新所使用的测量值yk为真实测量值。然而,在辨识以后,测量更新中将没有实际数据可用,全是预测值。此时,测量值yk会被预测值替换,预测值计算如下
(14)
式中q、r——标准差
randn(i,j)——产生标准正态分布的随机数或矩阵的函数,返回一个i×j阶随机项矩阵

1.2 渐消UKF主轴温升快速辨识算法
由1.1节可知,渐消UKF算法在增益矩阵Kk中引入了渐消因子αk以区别于传统UKF算法。对于不准确的系统模型,当前测量值对预测值的修正作用减弱,而先前测量值的修正作用相对增强,是导致系统发散的主要原因。为了减轻模型误差对Kalman滤波的影响,通过在滤波时渐消因子的引入使增益矩阵增大αk倍,从而在状态估计时增强当前测量值的作用,减轻先前测量值对系统的影响。其中,渐消UKF算法的关键是渐消因子的选择。
在Kalman滤波中,测量向量yk在k时刻的残差序列和协方差阵为
(15)
(16)
依据Kalman滤波最优理论[23],如增益阵Kk是最优增益阵,则新残差列应保持处处正交[24],即
(17)
对于不准确的系统模型,真实残差协方差阵与计算得出的理论值存在不一致,无法保证残差的自相关函数等于零。因此,本文通过对增益阵Kk的实时调整来保证残差序列相互正交,使渐消因子得到不断的修正,即
(18)
如果Pxkyk-KkVk=0,则可得
(19)
对式(19)进行求迹运算,得
(20)
为使状态估计更加平滑,引入弱化因子ρ来避免渐消因子αk的过调节,即
(21)
其中

(22)
式中ξ——遗忘因子,取0.95
ρ——弱化因子,取3[25]

(23)
则式(21)、(22)可改写为
(24)
(25)
滤波新息的理论方差应与实时识别的方差近似相互匹配,则约束等式为
(26)

(27)
式(27)各分量经归一化后基本相等,则化简后的等式为
(28)
由式(28)可得

(29)

1.3 自适应规则
非线性参考模型只能近似描述实际变化而无法准确反映,并且在测量过程中难免会出现随时间变化的测量误差,因此将协方差阵Q和R定为常量会导致改进渐消UKF算法的发散。本文提出一种改进的AFUKF算法,通过动态调整协方差阵Q和R,可以获得更好的滤波性能。自适应规则流程如图1所示。

图1 自适应规则流程图Fig.1 Flow chart of adaptive law
(30)
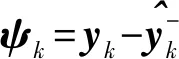
在以上策略中,Q和R调整方法为:如果γk<-H,Q以固定速率(c>1)增大,即Qupdate=cQ。对于R来说,如果ψk>0,则增大R,反之亦然;在增大或减小R时,首先设置一个调整步长Rstep,然后用步长搜索以找到适当的R,使得|γk|≤H。如果γk>H,调整方法与上述类似,Q以固定速率(c∈(0,1))减小,即Qupdate=cQ;对于R来说,如果ψk>0,则减小R,反之亦然。R的调整方法与上述相同,通过对Q和R的调整,使得|γk|≤H。

1.4 系统状态模型和测量模型
根据热模态理论[8],对于热系统,其瞬时传热过程描述如下

(31)
式中C——热容矩阵
H——热阻抗矩阵
W——热负载向量
T(t)——温度向量
t——时间
式(31)可以通过解下列方程式求解
HMr=brCMr(r=1,2,…,n)
(32)
式中Mr——特征模式向量
br——热特征值(b1 则式(31)的解可以表示为 (33) 式中T0——初始温度向量 当T0=0且W(ζ)为阶跃负载时,式(33)可以简化为 (34) 因此,式(34)可转换为 (35) 式中s——任一温度测点位置坐标 T(s,t)——t时刻位置s处温度测点的瞬态温度 T∞(s)——位置s处温度测点的稳态温度 Dr——常量,只与材料的热物理性质和初始温度有关 br(s)——与热系统的综合物理性质相关的常量 使用式(35)来表示热系统的瞬态温度分布,如果在测量温度时没有外界干扰,式(35)中从2到n的高阶项会迅速衰减,因此,可以保留第1项来近似表示瞬态温度分布 T(s,t)=T∞(s)+D(s)exp(-b(s)t) (36) 将温升模型转换为离散状态空间模型,假设状态向量x=(T,b,T∞)T,则离散温升模型为 (37) 机床主轴选点温升曲线可以在辨识时间内通过改进的AFUKF算法得到,并在辨识时间后通过改进的渐消UKF算法获得。为了衡量温升曲线预测精度,选用给定时间段内预测温度与测量温度之间的均方根误差为 (38) 式中Te(k)——kΔt时刻的预测温度 To(k)——kΔt时刻的测量温度 图2 不同采样时间下均方根误差随辨识时间变化曲线Fig.2 Changes in RMSE with different identifying times in different sampling periods (1)在时长为I1Δt的辨识时间内,使用改进的AFUKF算法,根据温度测量值,动态调整变量Q和R,并对所选温度测点进行预测,得到变化曲线。 (2)计算预测精度。将采样时长N1Δt下的预测温度与测量温度代入式(38),计算两者的均方根误差σ1。 (3)加大辨识时间,使其变为I2Δt,I3Δt,…,IgΔt,且满足I1 (5)通过图2可以看出,对于4个不同的采样时长,均方根误差均在辨识时间Ig-2Δt时刻呈现最小值,则可以判定该辨识时间为最短辨识时间。 当判别最短辨识时间后,即可以停止主轴热平衡试验,利用最短辨识时间内采集的主轴选点温升数据,使用改进的AFUKF算法就能够准确预测主轴选点温升,大幅度减少热平衡试验时间。 为了验证基于改进的AFUKF算法主轴温升快速辨识方法的可行性和有效性,依据ISO 230-3[26]数控机床热平衡试验相关标准,进行立式机床的主轴热平衡试验,通过试验获取所需温升数据。图3为机床主轴热平衡试验系统。在立式机床的不同位置布置了10个温度传感器来测量温度,所有温度传感器均为PT100型,如图4所示,表1为温度传感器位置说明。测量温度由数据采集系统记录,然后在计算机中进行处理和分析,并在计算机上执行基于改进的AFUKF的快速主轴温升辨识过程。 图3 机床主轴热平衡试验系统Fig.3 Thermal equilibrium test system of machine tool spindle 1.数据采集系统 2.温度传感器 3.立式机床 4.计算机 图4 温度传感器布置Fig.4 Location of temperature sensors 温度传感器编号测温点布置位置1~5主轴前轴承端盖表面6、9主轴套筒7主轴缸筒末端8主轴电机10主轴下端11环境温度 在室温为17.9℃时,机床主轴以5 000 r/min速度空转,开始热平衡试验。温度传感器的采样间隔Δt设置为1 min,每分钟记录一次温度测量数据,直到机床达到热平衡状态。本文提出基于改进的AFUKF算法主轴选点温升快速辨识方法,是针对某一点温度测量值进行处理的方法,因此对每个点来说都是独立的,对于某个辨识点来说,算法只需该点的温度测量值,而无需其他点的温度,所以其他测点的温度对所需辨识点没有影响。在本文热平衡试验中,布置了10个测点,每个测点均可作为辨识点,来验证算法的可行性。选择传感器5验证所提出算法,其他点的温升曲线以相同的方式预测。 图5 主轴选点的温度测量数据Fig.5 Measured temperature of spindle selected point 图6 不同采样时间下均方根误差随辨识时间的变化曲线Fig.6 Changes in RMSE with identifying times for different sampling periods of selected point 通过改进的AFUKF算法,计算得到在40、45、50、55 min采样时间下均方根误差随辨识时间的变化曲线,如图6所示。从图6可以看出,在辨识时间28 min处,均方根误差均为最小。根据最短辨识时间的判别规则,可以判断出28 min为该点温升曲线的最短辨识时间。因此,可以在28 min内准确预测选点的温升变化,而如果不使用本文算法,则需要大约400 min才能获得从机床启动到达到热平衡的温升变化。 在28 min辨识时间内,采用改进的AFUKF算法来辨识选点的温升。参数Q和R分别调整为diag(10-7, 10-7, 10-7)和1.932×10-9。图7为基于改进的AFUKF算法使用28 min辨识时间内的测量温升数据所得到的预测温升和测量温升变化曲线比较情况 ,使用稳态温度和达到热平衡时间(当温度达到最大温升的95%时的时间)来比较选点的预测温升和测量温升。预测的稳态温度为26.797℃,热平衡时间为197 min。测量的稳态温度为26.7℃,热平衡时间为195 min。本文算法稳态温度的偏差为0.097℃,热平衡时间偏差为2 min。预测结果表明,本文算法取得了良好的预测效果,能够使用28 min的测量温升数据准确预测400 min的热平衡试验的温升数据,大幅缩短了热平衡试验时间。 图7 测量温升与本文算法的预测温升曲线比较Fig.7 Comparison of measured and estimated temperature rises of selected point based on proposed algorithm 另外,对于状态向量x=(T,b,T∞)T,在温升辨识过程中获得了参数b和T∞的值,如图8、9所示。从图8、9可以看出,预测变量b和T∞分别收敛于0.016 min-1和26.797℃,证明本文算法在预测主轴选点温升时具有很好的收敛性。 图8 预测变量b的变化曲线Fig.8 Changing curve of estimated variable b 图9 预测变量T∞变化曲线Fig.9 Changing curve of estimated variable T∞ 通过计算得到总采样时间的不同辨识时间下预测温度与测量温度之间的均方根误差。图10为在总采样时间内均方根误差随辨识时间的变化曲线,从图10可以看出,辨识时间28 min的均方根误差最小,约为0.129 1℃。该时间与基于选点温升的快速辨识的时间相同。因此,可以证明本文提出的基于改进的AFUKF算法的温升快速辨识方法是有效的。 图10 总采样时间内均方根误差随辨识时间的变化Fig.10 Changes in RMSE with different identifying times in a sampling period of 400 min 在温升辨识过程中,传统渐消UKF算法与改进的AFUKF算法使用相同的初始化参数。进行选点温升快速辨识时,使用传统渐消UKF算法,在50、55、60、65 min的采样时间下均方根误差随辨识时间的变化曲线如图11所示。由图11可知,在辨识时间32 min处均方根误差均为最小。 图12为在辨识时间32 min处传统渐消UKF算法预测温升和测量温升变化曲线比较情况,从图12可以看出,虽然使用传统渐消UKF算法对所选点的最小辨识时间仅为32 min,但是在32 min辨识时间下预测温升与测量温升有较大偏差。基于改进的AFUKF算法下最短辨识时间28 min内的预测温升更接近于测量温升(图7)。原因在于传统渐消UKF算法,仅考虑渐消因子中对角元素的信息,导致残差信息不对称,而测量噪声和过程噪声的协方差R和Q保持固定不变的话,则会导致协方差Q、R与实际系统中的真实协方差不匹配,从而导致算法性能下降甚至发散,使得在最短辨识时间32 min内的预测温升与测量温升出现大的偏差。而改进的AFUKF算法因为通过残差归一化自动更新渐消因子,同时引入自适应调整规则,使得在进行温升预测时,得出的主轴温升预测结果符合实际的温度变化,因此,基于改进的AFUKF的快速辨识方法优于传统渐消UKF方法。 图11 传统渐消UKF算法不同采样时间下均方根误差随辨识时间的变化曲线Fig.11 Changes in RMSE with identifying times for selected point based on normal fading UKF in different sampling times 图12 测量温升与传统渐消UKF算法预测温升 曲线比较Fig.12 Measured and estimated temperature rises of selected point based on normal fading UKF (1)基于改进的AFUKF的温升辨识方法可以在更短的时间内快速预测机床主轴选点的温升变化。 (2)首先使用残差归一化处理自动更新渐消因子并将其引入增益矩阵,以减小系统模型偏差对估算精度的影响,增强滤波器的稳定性;其次通过使用自适应规则,动态调整协方差矩阵Q和R,减少外部扰动对温升预测的影响,获得了更好的滤波性能。 (3)使用立式机床验证所提出方法的可行性和有效性,试验中选定主轴上的一个点,得到28 min为该选点的最短辨识时间,利用该最短辨识时间下的测量温度所预测的主轴温升,与400 min时间段内测量温升之间的均方根误差为0.129 1℃、稳态温度之间的误差为0.097℃。试验结果表明,本文提出方法是有效的,应用于主轴热平衡试验,能够大幅度提高试验效率。1.5 辨识方法设计



2 试验验证
2.1 试验



图5为传感器5的测量温度变化情况,总测量时间约为400 min。

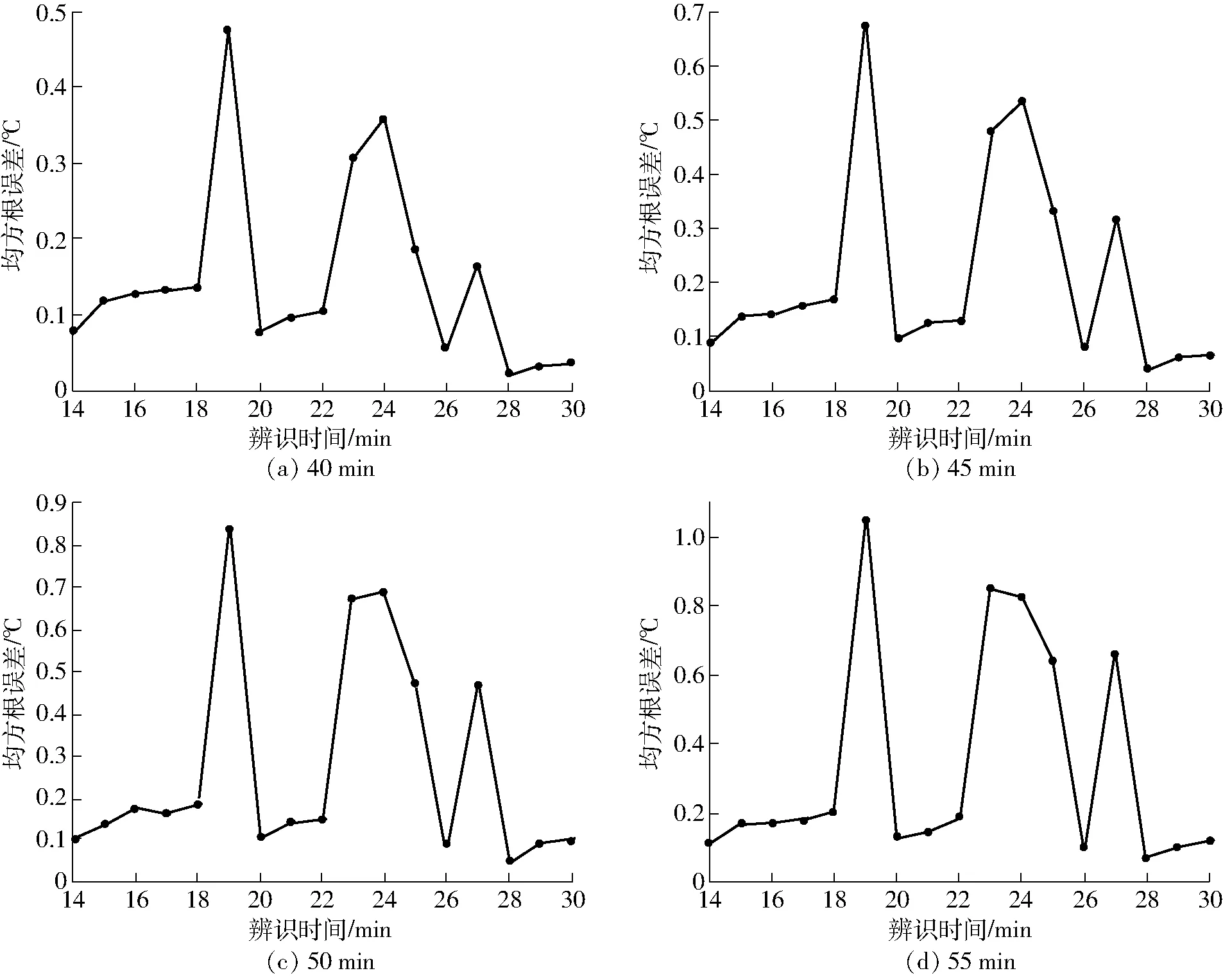




2.2 对比分析

3 结论
