基于混合水平集的脑胶质瘤分割方法

贺江琳，刘世伟，王星月，岳晴，王远军

上海理工大学医学影像工程研究所，上海200093

前言

脑胶质瘤通常呈弥漫性浸润生长，范围广泛，边界不清。受累区域的脑组织肿胀，沟变浅或消失，脑室变小。病变早期，脑胶质瘤占位效应常不明显，中线结构常没有移位；病变中、晚期可表现出占位效应，若病变偏一侧，占位效应征象可较早出现。肿瘤细胞多侵犯大脑半球两个或两个以上的部位，皮层及皮层下白质均可受累［1-2］。

由于脑胶质瘤的边界模糊，其磁共振（Magnetic Resonance,MR）图像分割有很大的难度。因此，为提高肿瘤分割的准确性，研究人员提出上百种图像分割的方法，文献［3］详细讨论了学者们提出的经典分割方法。近年来，国内外研究人员关于脑肿瘤分割也提出不少新颖的方法，包括K均值聚类和模糊C均值聚类的分割方法［4］、基于梯度幅度的分水岭分割法［5］、形态学阈值分割法［6-8］、基于Hough 变换定位与遗传算法［9］、基于灰度分布的分割方法［10］、基于学习的方法［11-13］等。实践证明，这些方法对于脑肿瘤的分割有明显效果，在临床上发挥了一定的作用，但是现在已有的任何一种分割算法在分割图像时，都难以取得比较满意的成果，结合多种算法的分割方法是目前研究的主要方向。1988年Kass［14］基于偏微分的方法提出的活动轮廓模型对图像分割领域产生了深远的影响，使得近年来，基于偏微分方程的图像分割方法成为研究的热点。后来随着水平集方法的提出，几何活动轮廓模型与水平集方法相结合的曲线演化方法成为图像分割领域的焦点，其中分割的快速、精确、自适应和鲁棒性成为研究注重的重点。

本研究主要对基于活动轮廓模型的分割算法展开研究与讨论，并提出一种基于边缘检测的活动轮廓（Geodesic Active Contours,GAC）模型与局部图像拟合（Local Image Fitting,LIF）模型相结合的混合水平集分割方法。

1 基于水平集方法的分割模型

1.1 水平集函数

水平集的方法最早是由0sher 和Sethian［15］提出的，其基本思想是将平面闭合曲线隐含地表达成三维连续函数曲面的一个具有相同函数值的同值曲线，用连续演化曲线来表达目标轮廓，并定义一个能量泛函使得其自变量包括曲线，从而实现将图像分割过程转换为求解能量泛函的最小值的过程。

给定一个常数c，定义水平集函数为ϕ(x,y,t )，c，c称为水平集函数值，当c=0 时，称{(x,y)|ϕ(x,y,t)}=0为零水平集。水平集函数常初始化为符号距离函数，即ϕ(x,y)=±d(x,y)，其中，d(x,y)表示点(x,y)到轮廓线的距离，并且符号距离函数满足 |∇ϕ|=1。任意给定平面一条封闭曲线，相应的符号距离函数如图1所示。

图1 符号距离函数Fig.1 Symbol distance function

1.2 C-V（Chan-Vese）模型

Mumford 和Shah［16］于1989年提出M-S 模型，该模型充分考虑了图像数据、初始估计、目标轮廓以及基于先验知识的约束等因素，在适当初始化后可以自动收敛，且对初始轮廓位置不敏感。但由于函数表达式本身的限制，该模型求取极小值比较困难，不能很好应用于实际。据此，Chan 和Vese［17］针对M-S模型的缺点，进行改进和简化，提出基于区域信息的活动轮廓模型：C-V模型。

C-V 模型假设待分割图像I(x,y) 可以被闭合曲线C分为两种同质区域，即目标区域以及背景区域。设这两个区域的平均灰度值分别为c1和c2，该模型对应的拟合能量函数如下：

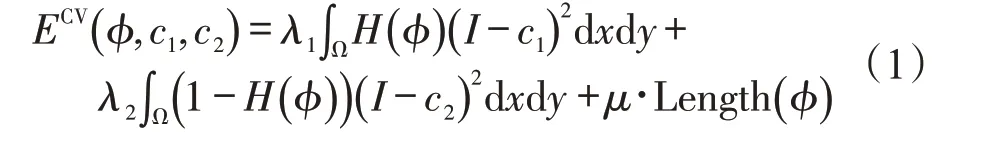
其中，H(ϕ) 为Heaviside 函数，Ω 为待分割灰度图像I(x,y) 的定义域。当闭合轮廓线处于两个同质区域的边界时，ECV达到最小值。根据变分法和Euler-Lagrange方程，对式（1）求解最小值，可以得到水平集函数的演化方程为：

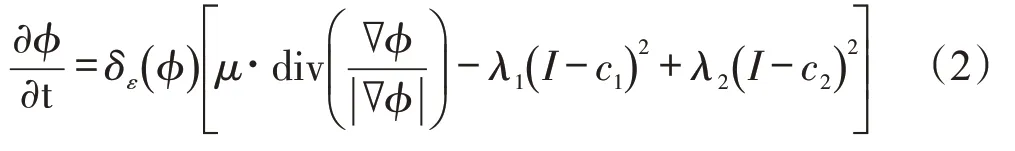
其中，c1和c2按如下方式进行更新：

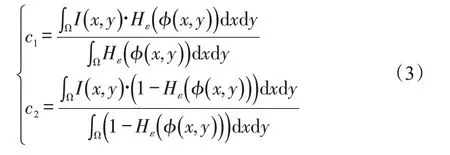
C-V模型充分利用图像的全局灰度信息，具有全局特征，可以自动检测图像的内外边界，并且有很好的抗噪能力。但在现实中，大量真实图像的灰度分布是不均匀的，因此，传统的C-V模型无法得到满意的结果。

1.3 LIF模型

为了解决灰度不均匀图像的分割问题，Zhang等［18］提出LIF模型，该模型是一种嵌入图像局部信息的区域活动轮廓模型，利用分片光滑函数来近似待分割图像I(x,y)。对于图像区域Ω 中的一点(x,y)，引入水平集函数ϕ(x,y)，LIF的能量泛函形式如下：

其中，ILFI(x,y) 为局部拟合项（Local Fitted Image,LFI），定义如下：

其中，m1、m2是图像在点(x,y)处的两个局部平均灰度值，即：

其中，Wk(x,y)为矩形窗口函数，通常采用截断高斯窗口Wσ(x,y)，其大小为(4k+1)×(4k+1)，k为小于σ（标准差）的最大整数。通过变分法与最速下降法最小化式（4）可得相应的水平集函数演化方程：

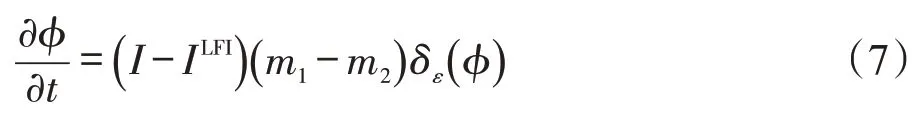
为了考虑水平集函数的正则性，获得更好的分割效果，需要考虑重新初始化的问题。Li 等［19］提出改进的变分水平集方法，可以避免重新初始化，也可以通过高斯滤波正则水平集的方法，对水平集函数施以高斯滤波处理，能够光滑水平集函数中的正则项，从而允许灵活地初始化水平集，实现快速分割［18,20］。因此，在LIF模型中，通常采用高斯滤波的方法来实现对水平集符号距离函数的正则化过程以及保证水平集演化的稳定性。

当水平集函数固定时，m1和m2的取值是一种与σ大小有关的局部量。这种局部特征使得该模型在分割灰度不均匀的图像时可以取得较好的效果，其分割结果优于C-V 模型。此外，相比于LBF 模型，LIF 模型的计算量大大缩减，提高计算效率，不足的是，LIF 模型对初始轮廓线的位置非常敏感，其分割结果依赖于初始轮廓线的位置、大小以及形状。

1.4 GAC模型

GAC模型是在Snake模型的基础上提出来的，该模型是一种典型的基于边缘检测的能量模型，其基本思想是利用黎曼空间中的测地线概念，把寻找图像中的边界线问题转化为寻找一条加权弧长的最小值［21］。由于水平集的引入，GAC模型消除了Snake模型对自由参数的依赖，在曲线演化过程中能够自动处理拓扑结构的变化，并检测到有明显轮廓的物体边界。

对于给定的待分割图像I(x,y) ，GAC 模型的能量泛函定义为活动轮廓线C的加权长度，具体形式如下：

其中，L(C)表示闭合曲线的弧长，s表示闭合曲线的弧长参数，g表示边缘检测函数。引入水平集函数ϕ(x,y,t)并代替曲线C，最小化式（8）可得相应的梯度

下降流：

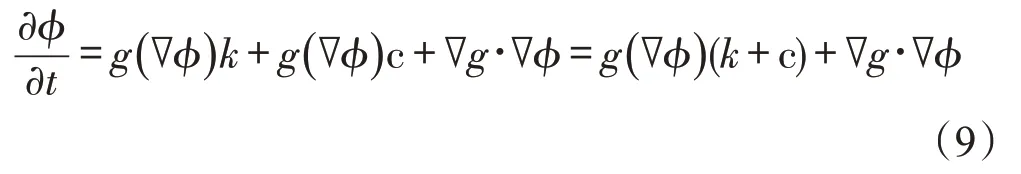
其中，k为曲率，c 是一个可选常数。c 的取值决定着式（9）中恒定速度项g(∇ϕ) c 的运动方向：其方向总是恒定指向曲线的内部（c ＞0）或外部（c ＜0），GAC 模型中添加此项有利于曲线在演化时，能够在一定程度上缓解曲率为负的情况下对曲线运动带来的阻碍作用，从而有利于对凹陷边界的正确检测。

相比于Snake模型，GAC模型不再依赖于曲线参数，并且可以自动适应曲线的拓扑结构变化，能够有效分割边界清晰的物体。但是GAC模型在分割弱边缘或离散边缘的物体时容易产生边界泄漏的问题，并且该方法对初始轮廓线的位置要求较高，一般选择在待检测物体的附近，否则分割结果将不太理想。此外，该模型中恒定速度项c 的取值必须为先验参数，c 值过大将导致曲线在图像较为平滑区域产生错误的分割结果，因此参数c 的取值需要慎重对待。

2 本文模型

由于图像的边界和区域的重要性，在分割过程中既要保证图像区域信息的完整，也要保证图像边界信息不丢失，所以结合LIF模型与GAC模型，本文提出一种新的混合水平集模型。

本文的水平集能量模型是LIF模型与GAC模型的一个线性组合，具体形式如下：

其水平集演化偏微分方程为：

式中，α的取值决定着模型在分割时，LIF 模型与GAC模型各自发挥作用的大小。当α=0 时，该模型就成为GAC 模型；当α=1 时，该模型则变成LIF 模型。合理选择α值的大小，本文模型可以改进GAC模型中对弱边缘以及离散边缘产生的边界泄漏的问题；并且综合运用图像的局部区域信息，发挥LIF 模型的优点，减少模型的计算量，从而提高曲线演化的效率。此外，常数速度项cg( ∇I)δε(ϕ)里c 的取值一般为先验参数，但由于c 值的大小不易具体确定，若c 值过大将导致曲线在图像较为平滑区域产生错误的分割结果。因此，本文采用变系数V(I)来代替常数c［22］。V(I)的定义如下：

其中，β1与β2为各项的权重系数且β1=ω∙β2，H为Heaviside函数，的定义如下：

采用变系数的方法可以提高模型检测图像凹陷边界的能力，更好地保护弱边界，抑制分割曲线渗透弱边界的问题，并且提高曲线的演化速度。变系数V(I)只改变原常数c 的大小，不改变其正负。

另外，在传统水平集方法中，为了保持符号距离函数 ||∇ϕ=1 的优良性质，我们有必要使水平集函数在演化的过程中始终近似于符号距离函数。早期往往采用周期性的重新初始化方法，此种方法极大地提高了模型的计算复杂度，而且重新初始化的操作时间和执行频率难以具体确定。因此，本文采用Zhang 等［18］提出的一种高斯滤波正则水平集函数法来实现水平集函数的正则化，即通过对水平集函数前一次迭代的结果进行高斯滤波来实现正则化过程，并且为了简化符号距离函数，水平集函数初始化为如下形式：

其中，d 为大于零的常数，且d＞2ε是定义的正则的Dirac函数δε的宽度。

本文模型的算法可归纳如下：（1）采用C-V 模型预处理脑胶质瘤MR图像，提取脑组织；（2）根据经验设置迭代次数n，参数的具体取值见本文第3 节；（3）初始化水平集函数ϕ(x,y,t) ，具体形式如式（15）；（4）通过式（12）来演化水平集函数ϕ，每次演化结束后对水平集函数ϕ进行高斯滤波；（5）若程序的迭代次数等于n，算法则停止，否则重复（4）。

实验过程中，由于MR图像中非脑组织区域的部分灰度信息会对脑肿瘤分割产生干扰，因此本文在预处理时采用C-V模型与数学形态学相结合的方法提取脑组织，为后续的脑肿瘤分割实验消除一定的影响因素。此外，迭代次数n的取值十分重要，本文通过多次实验验证后，从中选择最优的数值作为标准的迭代次数。为避免初始轮廓线位置对分割实验结果带来的影响，本文在实验中采用手动设定初始轮廓线圆心位置的方式。

3 实验结果与分析

本文实验数据为一组格式为DICOM文件的MR图像，其数据矩阵大小为512×512，数据类型为16 位无符号整型，该序列共有248 幅MR 图像，本文选取其中可以看到脑肿瘤的30幅MR图像进行实验。实验环境的操作系统为64 位的Windows 10，处理器为Inter(R) Core(TM) i3-2350M CPU(2.30 GHz)，内存为8 GB；采用的软件为MATLAB R2014a，本文脑肿瘤分割算法的所有代码均在此平台上运行。

为定量评价分割结果，本文使用有经验的临床医生手动分割结果作为评价分割准确性的标准。本文使用的定量评价指数分别为Jc（Jaccard Index,Jc）指数与Dice相似性系数（Dice Similarity Index,DSI）。

Jc 指数的定义为：

其中，Rdoc为临床医生手动分割的结果（评价标准），Rpro为算法分割的结果（评价对象）。算法分割结果越准确，则Jc 值越接近1。

DSI定义为：

式中，Rdoc与Rpro表示的意义与式（16）一样，算法分割结果与评价标准重合度越高，则DSI越接近1，表示分割结果越精确。

在实验过程中，本文依据式（12）和式（13）演化水平集函数，相应参数的取值为：α=0.8，ε=1.5，β2=0.28，ω=0.1 ，迭代的步长Δt=0.1，迭代次数n=200。此外，用于计算LIF 模型中局部均值的截断高斯窗口W(x,y)σ的σ取值为3，k为1，即采用窗口大小为5×5的高斯窗口。除参数α、迭代次数n与迭代步长Δt，其余参数取值均保持不变的情况下，分别采用本文的模型（α=0.8，n=200）、LIF 模型（α=1，n=600）与GAC 模型（α=0，n=100，Δt=3.0，式（12）中常数c=0.2）对预处理后的MR 图像进行脑肿瘤分割。本文主要展示实验中4 幅脑肿瘤MR 图像的分割结果，图像相关实验结果如图2所示。

由以上实验结果可知，在分割同一幅图像时，LIF模型需要的迭代次数大于本文模型，且分割结果稍差于本文模型，在图像弱边缘处无法得到精确的分割结果；而GAC 模型分割图像时，速度较慢，需要增加迭代的步长，从而减少迭代次数，并且在分割凹陷边界时，仅采用GAC 模型往往不能得到正确的分割结果。本文模型有效地结合GAC模型与LIF模型的优点，在曲线演化过程中，可以减少算法的计算量，改善LIF 模型与GAC 模型在弱边缘处产生的边界泄漏问题，提高算法的分割精度。因此，在相同迭代次数的情况下，本文模型的分割结果优于GAC 模型与LIF模型。

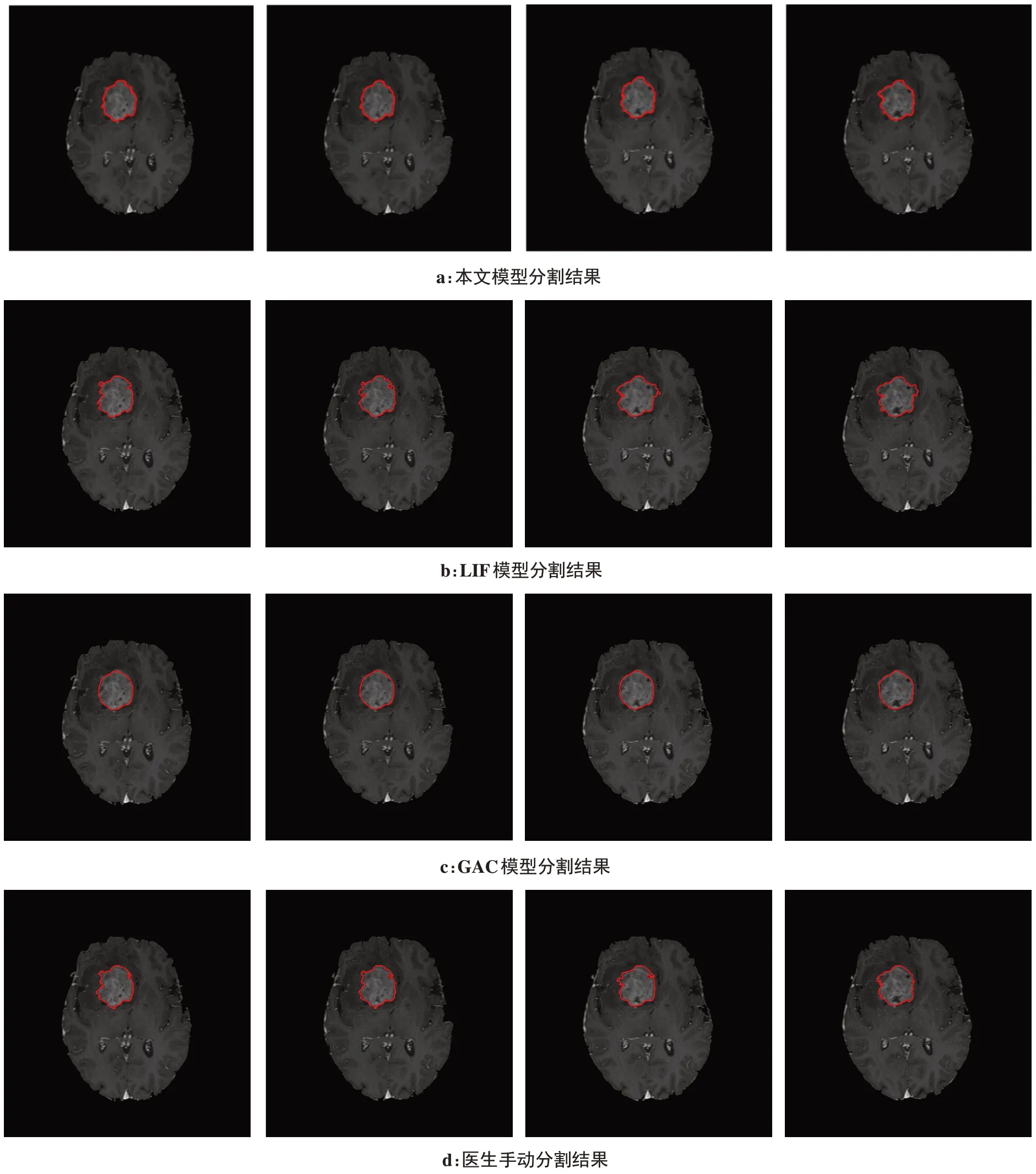
图2 3种模型分割结果图Fig.2 Segmentation results of 3 models

本文采用医生的手动分割结果作为评价标准。对本文的实验分割结果做定量验证分析，相关数据如表1所示。从表1可以看出，在两个定量评价指标中，本文模型的Jc 的平均值为91.00%，DSI的平均指标为95.27%。两者的数据皆接近于1，高于GAC 模型与LIF模型的定量评价指标，说明本文的分割结果较为精确，即本文模型在分割图像时具有一定的有效性。

4 结论

本文基于混合水平集算法分割脑肿瘤展开研究与探讨。首先，对传统的脑肿瘤分割方法进行简单的介绍。然后，以水平集算法为核心，分别介绍C-V模型、GAC模型与LIF模型，并将GAC模型与LIF模型的各能量项按一定加权比例结合起来，实现混合水平集算法。通过实验，我们得到了较好的分割结果，实验中的不足之处在于混合水平集模型对初始轮廓线的位置较敏感，需要手动确定其圆心位置，在以后的研究中，可以对此做进一步的改进。

表1 本文算法分割精度的定量评价（%）Tab.1 Quantitative evaluation of the segmentation accuracy(%)