三级供应链产品纵向质量管理微分博弈分析

王会会，周溪召 （上海理工大学 管理学院，上海 200093）

0 引言

随着市场上企业的不断涌现，消费者在面临众多的同类但存在异质性产品时，产品质量便成为首选的关键因素。同时，在社会化分工越来越细和产品生产全球化的今天，产品的完成往往需要经过许多厂家进行原料供应、零部件制造加工、商品销售等过程，这就形成了一条链式服务，而产品质量依赖于产品的生产流程及工艺。

鉴于质量管理的重要性，现已经有众多学者对供应链中的产品质量进行了相关研究。Chao[1]提出了如何进行质量改进激励和产品回购中质量契约设计以解决两级供应链中制造商与供应商质量控制决策；Liu Weihua[2]研究了二级供应链中供应商和制造商的质量控制问题；朱立龙[3-4]等基于Stackelberg博弈分析，探讨了在静态情况下三级供应链如何制定产品质量控制策略的问题，随后又基于委托代理理论和博弈论相关理论，研究了生产商和购买商的质量控制契约设计的问题；申强[5]等讨论了道德风险下制造商和供应商的质量控制与协调机制；马鹏[6]等探究了不同公平偏好行为下制造商和零售商的质量投资策略问题；高鹏[7]等分析了不同市场领导结构下二级供应链的质量决策问题；洪江涛[8]等运用微分博弈方法研究了两级供应链质量管理过程中博弈结构对均衡结果的影响，张翠华[9]基于质量偏好研究了集成商和提供商所组成的服务供应链的质量控制问题；王谦[10]等基于零售商是否共享质量检测水平信息，研究了非对称信息下由供应商和零售商构成的两级供应链的质量激励问题；温小琴[11]等研究了在中心化供应链和由制造商与零售商组成的两级分散化供应链中产品的质量选择和数量决策；范建昌[12]等研究了制造商CSR对由上游制造商和下游零售商组成的两阶段供应链中产品质量、产品需求和利益相关者经济业绩均衡运作结果的影响；赵荧梅[13]等研究了不完全信息下生产企业、经销商和政府部门对产品质量监管博弈相关问题。以上这些文献部分运用静态博弈来研究二级或三级供应链质量管理相关问题，部分采用微分博弈的方法，从动态角度分析二级供应链质量管理问题，但是基于微分博弈分析三级供应链质量管理行为的相关研究十分有限。基于此，本文选择由一个供应商、一个制造商以及一个零售商组成的三级供应链进行分析，建立上下游之间的微分博弈模型，并分析了三种不同决策情况下供应链系统的最优利润和产品质量以及边际收益对供应链系统的行为影响，有利于企业根据实际情况进行合作契约的选择与制定。

与孙健慧[14]研究进行比较，本文主要有以下不同：（1）其研究的是一个制造商、两个不同供应商构成的三级装备制造业供应链，而本文在此基础上引入零售商，研究了由一个供应商、一个制造商和一个零售商构成的一般性供应链质量管理问题；（2）其研究假设供应链收益与产品质量呈线性函数关系，而本文考虑广告宣传，并且假设供应链收益依赖于边际利润和需求，而需求是由供应商、制造商和零售商及产品质量决定。

1 问题描述与相关假设

1.1 问题描述

1.2 符号说明

Is（t）、Im（t）、Ir（t）：表示t时刻供应商、制造商、零售商在质量管理上的努力程度；

φ1（t ）、φ2（t）：分别表示t时刻供应商和制造商努力成本的补贴比例；

Q（t）：表示t时刻产品的质量，依赖于供应商和制造商的质量管理努力程度，为状态变量，其中，当t=0时，Q（0）=2；

πs、πm、πr分别为供应商、制造商、零售商的边际利润；

Js、Jm、Jr分别表示供应商、制造商以及零售商长期的总利润。

1.3 模型基本假设

（1）根据参考文献[15]对质量控制努力成本的假设，供应商和制造商在质量管理上的努力成本分别为Cs（t）=λ 2sI2s（t）和Cm表示供应商和制造商的质量管理努力成本系数；

（2）根据参考文献[16]对销售努力成本的假设，本文将零售商在广告宣传上的努力成本设为其中 λr＞0，表示零售商广告宣传努力成本系数；

（3）单位产品的质量与供应商、制造商的质量管理努力程度相关，具有动态变化的特点，所以假设单位产品质量变化过程的微分方程为其中α和β分别表示供应商和制造商质量管理努力行为对单位产品质量的影响程度；ζ表示外部原因造成产品质量的衰减系数，α、β、ζ＞0；

（4）假设市场需求受产品质量和广告宣传努力程度的影响，因此假定需求函数具有如下形式其中D0≥0为常数，表示产品的初始需求，μs、μm、μr分别表示供应商、制造商和零售商的努力行为对产品需求的影响系数，η表示产品质量对产品需求的影响系数，μs、μm、μr、η＞0；

（5）假设供应商、制造商和零售商具有相同的贴现率ρ，ρ＞0，他们的目标都是在无限区间内寻求利润最大化。

借鉴文献[17]，假设模型中所有参数都是与时间无关的常数，且博弈在无限时区的任何时段内，参与人面对的是相同的博弈，因此可将策略限制在静态策略。（为简化书写，下文不再列出时间）t

2 分散式决策情形

2.1 Nash非合作博弈情况下

在该情形下，供应商、制造商和零售商各自决策，都追求最大化利润，用上标N表示。决策过程为：供应商、制造商和零售商三方同时进行决策，此时，他们的决策问题分别为：

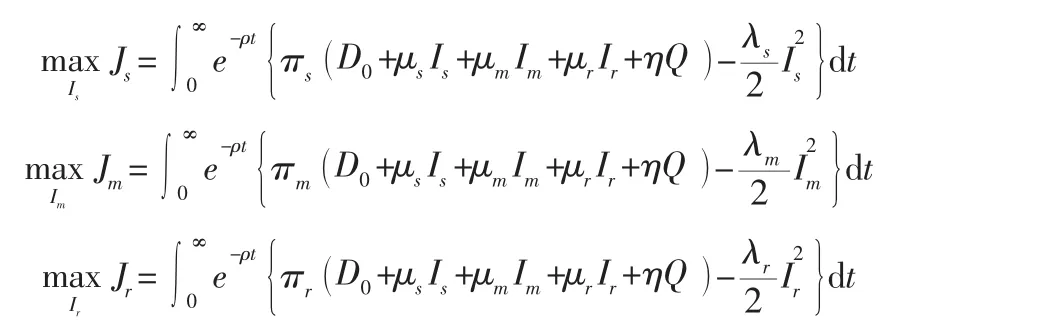
结论1：在Nash非合作博弈情况下，供应商、制造商和零售商的最优均衡策略分别为：

证明：参考最优控制[18]的求解方法，可知式均满足以下HJB方程，即：

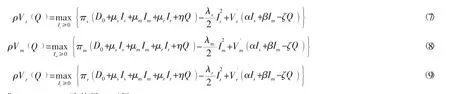
分别对式 （7） ～式 （9） 求Is、Im、Ir一阶偏导，可得：

将式 （10） ～式 （12） 带入式 （7） ～式 （9） 得：

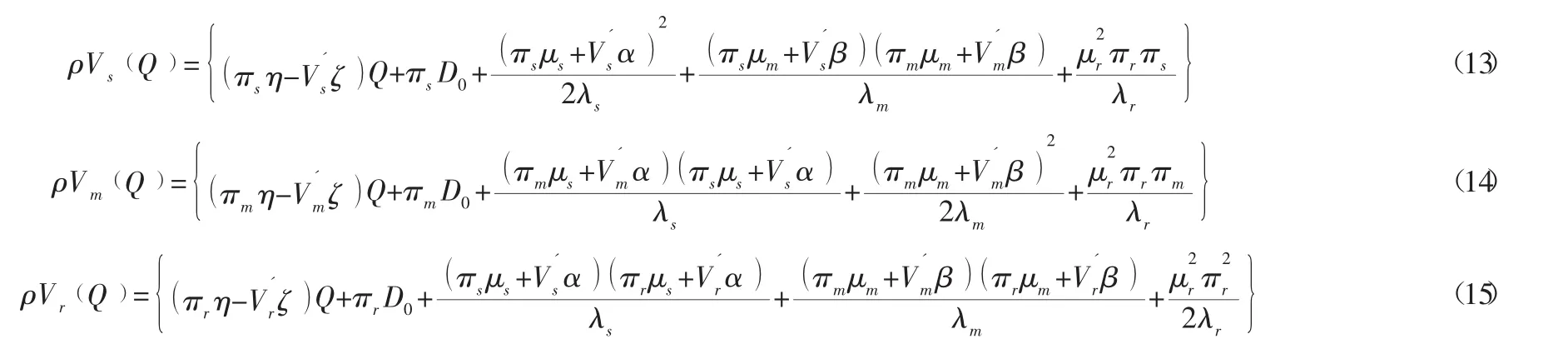
根据式（13） ～式（15） 微分方程的特点，推测最优收益函数Vs（Q ）、Vm（Q ）、Vr（Q ）是关于Q的线性解析方程，因而令Vs（Q ）=f1Q+f2,Vm（Q ）=g1Q+g2,Vr（Q ）=h1Q+h2中f1、f2、g1、g2、h1、h2均为常数，并且将其代入式 （13） ～式 （15） 整理可得：

对比式（16）～式（18）左右两边的同类项系数，整理可得：

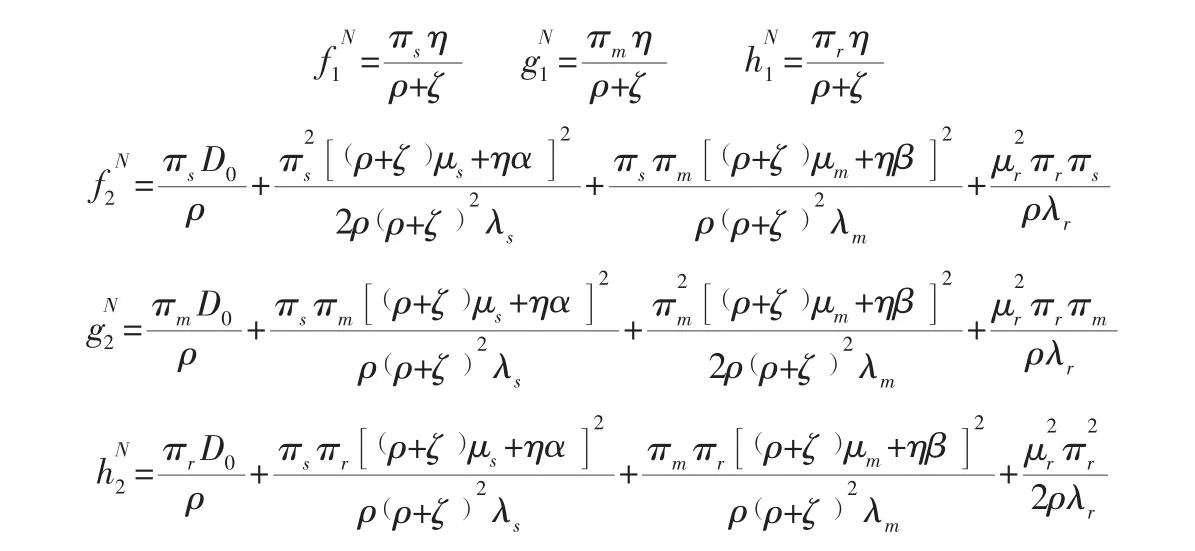
2.2 Stackelberg主从博弈情况下

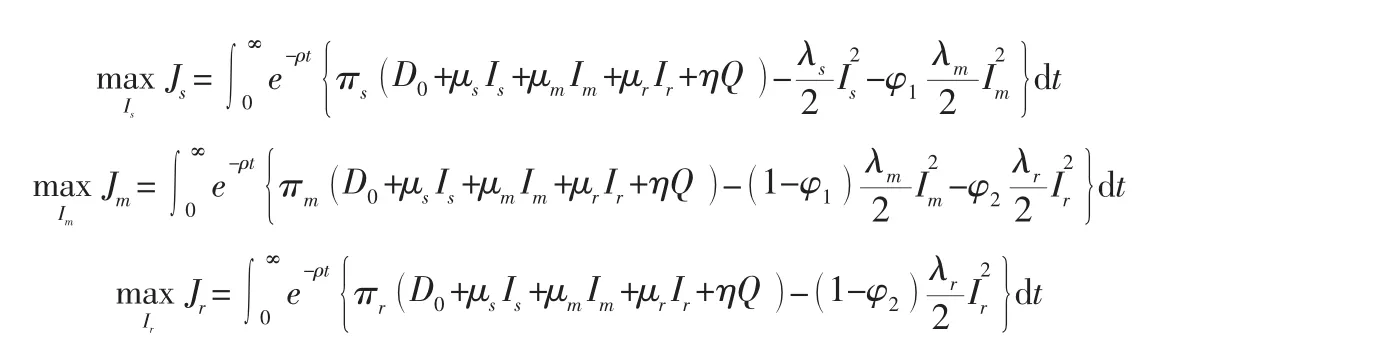
在该情况下，制造商和零售商独自决策以最大化各自利润，用下标S表示。决策顺序为：供应商、制造商、零售商。此时三方的决策问题为：

结论2：在Stackelberg主从博弈情况下，供应商、制造商和零售商的最优均衡策略分别为：

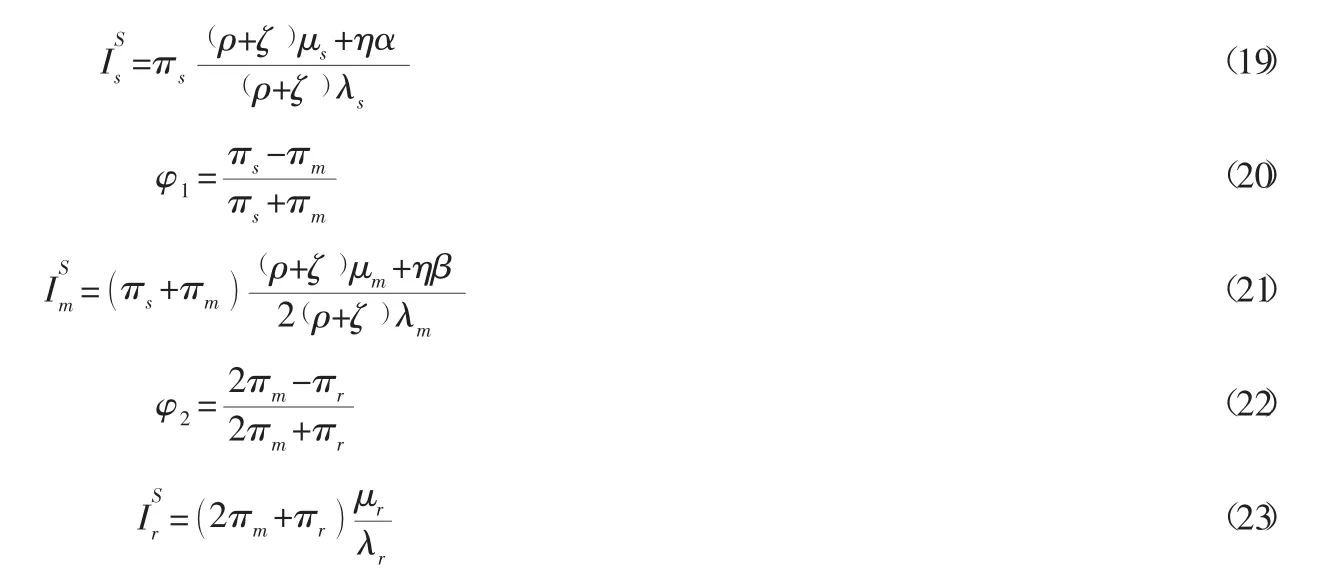
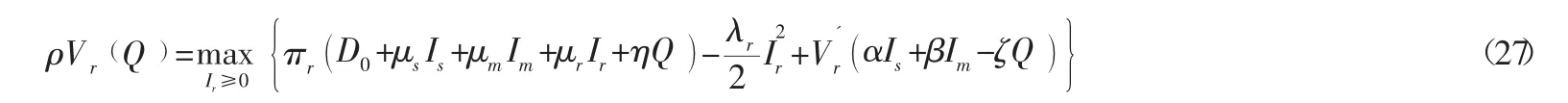
对式（27） 求Ir一阶偏导：

将式 （28） 代入式 （29） 中，可得：

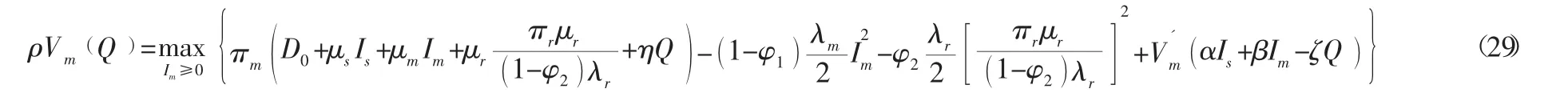
对式（29） 求Im、φ2一阶偏导，可得：

将式（28） 和式（30） 代入式（32） 中，并对Is、φ1求一阶偏导，可得：

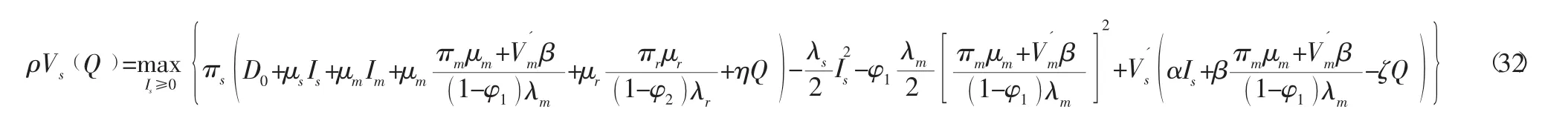
将式 （28）、式 （30）、式 （31）、式 （33）、式 （34） 代入式 （27）、式 （29）、式 （32） 可得：

根据式（35） ～式（37） 微分方程的特点，推测最优收益函数是关于Q的线性解析方程，令Vs其中f1、f2、g1、g2、h1、h2均为常数，并且将其代入式 （35） ～式 （37） 可得：

对比式（38）～式（40）左右两边的同类项系数，整理可得：

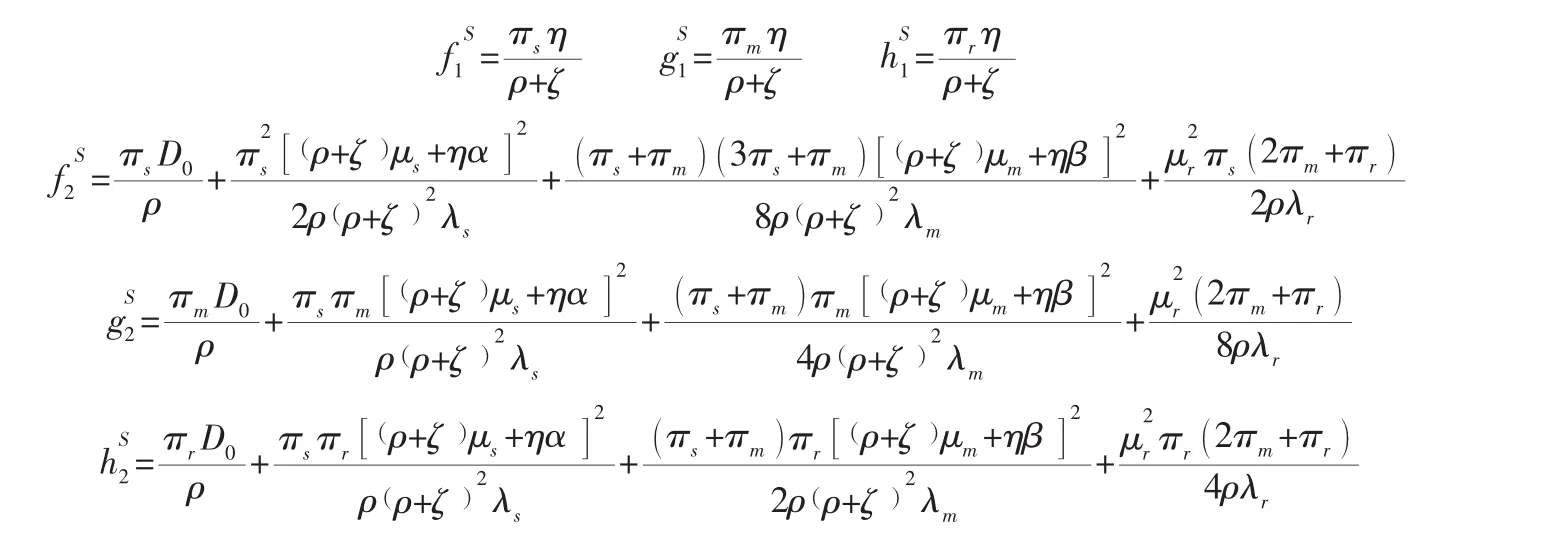
2.3 比较分析

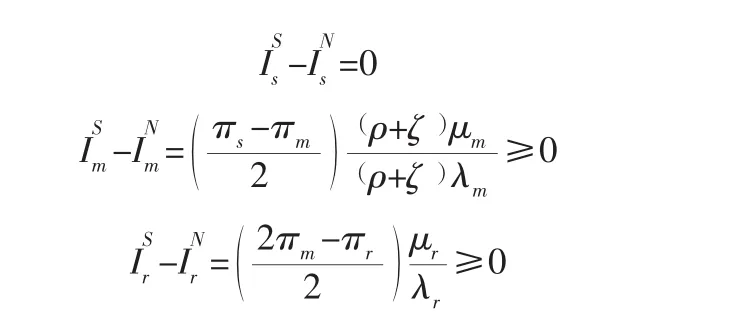
推论1表明，在分散式决策下，供应商的质量管理努力程度在Nash非合作和Stackelberg博弈情形下相同，同时成本分担比例随着供应商和制造商的边际利润的增加而增加，并且当时，供应商为制造商，制造商为零售商都相应地分担一定成本，因而制造商和零售商的质量管理努力程度在Stackelberg博弈情形下比Nash非合作博弈下得到加强；当πs≤πm时，供应商和制造商不但不会承担成本费用，而且会收取一定费用，在一定程度上降低其积极性，因而会造成制造商质量管理和零售商广告宣传的努力程度有所下降。

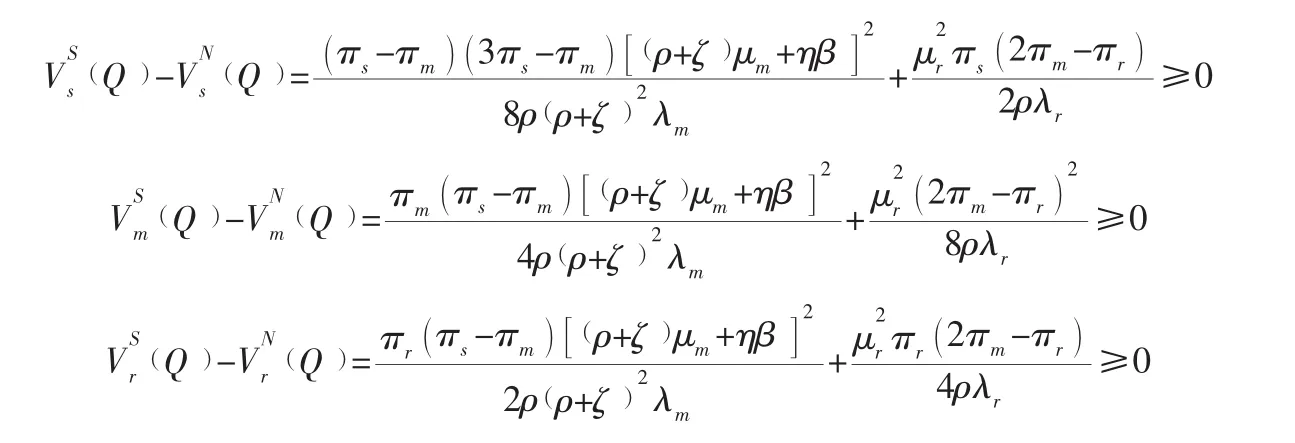
推论2表明，在分散式决策下，由结论2可知，在一定条件下，供应链系统（包括供应商、制造商和零售商）的利润最优值函数在Stackelberg博弈情形下比Nash非合作博弈下实现了Pareto改善。

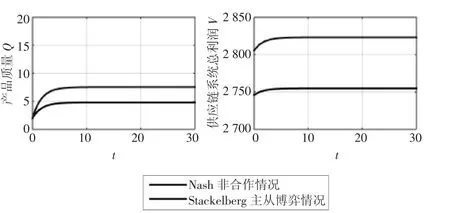
图1 两种决策下供应链产品质量和利润对比

3 算例分析

为了更加直观地说明供应商、制造商和零售商在分散式决策和集中式决策情况下各自质量管理努力行为和利润最优水平的变化，可利用数值仿真对上述微分模型进行分析。根据参考文献[14-15]相关数据取值，具体相关参数设置如下：λs=0.5,λm=0.5,λr=0.4,α=0.4,β=0.3,ζ=0.6,D0=20,μs=0.4,μm=0.6,μr=0.3,η=0.2,ρ=0.1,πs=4,πm=3,πr=4,Q（0 ）=2，其中 πs≥πm将相关参数代入相关结论及推论所给的解析式，借助Matlab R2017a可以给出3种不同博弈情况下供应链产品质量和系统总利润对比关系图（图1），供应商、制造商以及零售商分散决策情况下利润对比关系图（图 2）。

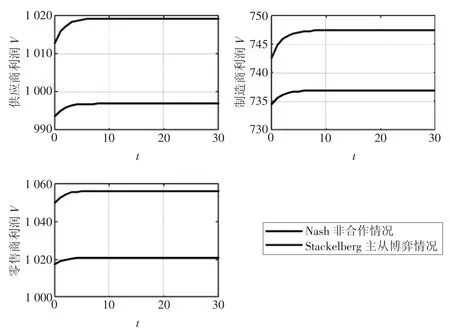
图2 成本分担前后供应商—制造商—零售商利润对比

从图1可看出，3种情况下产品质量和最优利润情况是：集中式决策情况下最大，无成本分担时的分散式决策最小，而分散式决策下有成本分担的Stackelberg主从博弈情况可以达到供应链系统利润的Pareto改善。

供应商、制造商和零售商集中式决策时，供应链系统的总利润及产品质量远大于两种分散式决策情况下系统的总利润，验证了前面理论推导的结果。集中式决策时供应链系统中产品质量增长迅速，而两种分散式决策情形下产品质量增加缓慢，这充分说明集中式决策优于分散式决策，可以为企业进行优质产品的生产提供参考。

从图2可以看出，借助有成本分担的Stackelberg主从博弈可以在一定程度上实现供应商、制造商和零售商利润的Pareto改善。这是由于供应商分担了制造商的质量管理成本，而制造商分担了零售商的广告宣传成本，因而最终可以促进零售商大力进行广告宣传，从而扩大市场需求，市场需求的增加最终将促进供应商、制造商和零售商利润的增加，因此使三方的利润都能达到Pareto改善。

4 结论

本文通过探讨由供应商、制造商以及零售商组成的三级供应链纵向产品质量管理的动态优化问题，为供应链上下游企业获取最优利润和生产优质产品提供了相关的理论依据。同时，随着产品生产企业的不断涌现以及交易方式的多样性，产品质量的提升不仅限于纵向供应链企业的决策，并且需要考虑横向竞争，因此，未来可以研究由双寡头制造商竞争与合作下的产品质量管理优化问题。此外，文中假设产品的边际利润为常量，而实际中，供应链节点企业之间的产品交易价格常常是供应链运营的决策变量，因此在现有模型中引入批发价格等决策变量，也是我们未来值得研究的问题之一。