基于区间直觉模糊数及多准则扰动的供应链众筹产品选择算法

张 凡，屈绍建，高 航 ZHANG Fan,QU Shaojian,GAO Hang

（上海理工大学 管理学院，上海 200082）

0 引 言

近年来众筹的发展风生水起，这种新型的融资方式被很多中小企业和项目发起者所采用。在电动汽车的充电桩安装方面众筹相较于其他的方式其推广作用更为显著[1]。在健康医药领域也有重要的应用，尤其对于医学研究的启动资金筹集方面有重要的助益作用[2]。从众筹的融资方式可以看出，它是通过网络平台作为融资的宣传方式和融资场所，与传统的融资方式有所不同，众筹所面对的投资者不再是少数的资本家或者政府，而是多数社会公民，这种融资的方式无形中增加了项目的成功率，所以现在很多的小微企业和项目在项目启动之初大多采取众筹的方式进行。参与众筹项目的投资者可以有很多人，所以对于每一个参与到项目中的人来说投资金额只是总额的一小部分[2]，这一点让普通公民参与投资的概率增大，也正是因为如此，众筹项目也逐渐走入了人们的视线中。现在国内已经涌现出很多的众筹网站，例如：点名时间、追梦网、京东凑份子等，由此可以看出众筹的发展已经深入到每个人的生活中。随着网络的发展越来越迅速，现在人们每天都可以在网络上浏览到很多的众筹项目，每一位投资者都会根据自己的一套准则来挑选适合的项目。挑选的准则一般来自心理和客观两个方面，心理的考虑准则一般包括投资者本身对于项目偏好和对项目发起者的信任，这两点对于投资者的最终选择起到很重要的作用，很多的投资者对于投资项目有自己独特的偏好比如偏好房地产项目、节能环保类项目等。导致这种现象的主要原因是由于国家政策和社会发展方向等客观的社会环境使得他们对这类众筹项目盈利前景看好。还有就是投资者对于项目发起人的信赖，很多投资者存在跟风和从众的心理，对于一些社会声誉很高的人发起的项目就会跟投，而客观的准则包括项目投资金额和项目的地理距离等。由于众筹项目的形式一般有投资型和回报型两种[3]，前者要求投资者提前投资一部分资金，后期可占有相应的股权；后者投资者可根据项目发起者提供的选择表进行选择投资，等到项目完成时可得到相应的产品及回报，但都需要投资者在项目进行前支付一定的金额，所以投资者需要根据自己的投资能力来选择投资项目。地理距离指的是投资项目进行的地点和投资者所在地之间的距离，如果这个距离太远就容易造成投资者不能监看到项目进行的程度，这就使得投资者的心理产生不安。虽然现在网络发达，投资者可以从网上呈现的相关数据了解项目的进行程度，但这存在着发起者和投资者之间信息不对称的可能，所以地理距离的远近也是一个重要的参考准则[4]。投资者在选择众筹项目时，所考虑的多准则之间其实也存在着相互的扰动现象。对于投资者而言如果只考虑其中的部分准则所做出的决策和考虑全部准则的结论是不一样的。正是由于这种现象使得投资者的决策环境变得更加复杂，相较于一般的多准则决策。对于一个投资者而言，如何基于多个参考准则从多个众筹项目中选择出最合适的众筹项目是一个亟待解决的问题。

由于众筹项目的特殊性投资者考虑的准则大部分都比较抽象，每一个准则对于不同的投资者都有不同的考虑，这些准则不能用具体的量来表示，因此对于整个多准则的决策问题建模造成了困难。而模糊决策算法的优势就是将抽象的量量化并且带入一系列的算法中[5]，对于众筹项目的多准则决策问题模糊决策算法刚好能够解决。所以本文提出以模糊集的方式替代每一个参考准则，每个决策者将自己的考虑准则表达成一个模糊集}的形式，通过这样的形式就可以将具有抽象特点的参考准则量化为具体的形式，便于对整个决策过程建模。对于多准则决策模型在模糊数学中已经有许多的研究人员构造出了很多的聚合算法[6]。例如：直觉模糊权重平均算法和直觉模糊权重几何算法等。这些算法在计算时可以考虑到待选项目的多个方面，然后通过算法中的聚合算式对每一个待选项目进行计算并得出聚合值，最后根据这些聚合值对每一个项目进行排序，聚合值最大的那个项目就是基于多个准则的条件下最适合投资者的。但考虑到决策环境的复杂性，这些提出的算法在实际运用的过程中产生了很多的问题，不能够满足实际的决策。所以后来学者们在算法上进行了改进，又提出了直觉模糊排序权重几何算法和直觉模糊排序权重平均算法。这些算法在一定程度上规避了之前算法的弊端，充分考虑到了模糊数的排序位次问题。

但是这些模糊算法到目前为止都没有涉及到多准则之间会产生相互的扰动问题，选择项目时参考准则之间的相互扰动会对结果产生直接的影响。例如一位投资者仅仅以地理距离作为参考准则在A和B这两个众筹项目中做选择，假设A较于B的地理位置更近，这位投资者可能就会选择A项目。但若投资者又将盈利能力同时作为一个参考准则可能最后选择的结果就不同了，这中间就涉及到投资者在地理位置和盈利能力这两个准则之间的权衡。所以在这篇文章中提出的基于区间直觉模糊数及多准则扰动的众筹产品选择算法就考虑到了这一点。本文从模糊集的角度来考虑准则间的扰动问题，模糊集之间的相互扰动可以考虑成两个模糊集之间的相互影响，即一个模糊集在加入另一个模糊集之后产生的变化。刻画的方法有很多，例如：欧几里得距离、汉明距离、特韦尔斯基比较模型[7]。通过这些模型可以使两个模糊集之间的扰动关系具体表达成数字，这样模糊集之间的扰动大小就更加清楚。

投资者选择众筹项目的过程是一个复杂的决策过程，而模糊决策的模型可以将其中不确定的信息进行量化并且聚合最后得出一个准确值。本文通过区间直觉模糊的形式对每一个众筹项目进行聚合计算，然后根据聚合值对所有众筹项目排序。通过模糊决策模型得出的聚合值综合考虑到了各方面因素，并且根据多准则间的扰动影响大小对每一个准则赋予不同的权重值。

1 预备知识

在这一节中首先回顾几个基本的直觉模糊数相关的概念和一些计算法则。

1.1 首先X是一个有限集，然后A-IFS可以被定义为：

式中的 μA（Xi）是一个映射，的隶属函数。而vA（Xi）是一个映射关系，vA:X→[0,1 ],的非隶属函数。其中隶属函数和非隶属函数符合约束条件：与此同时直觉模糊集A的犹豫度可以被表达为而且对于任意x∈X,0≤π （XA）≤1[8]。

2 对众筹项目的区间直觉模糊决策

2.1 模糊多准则决策

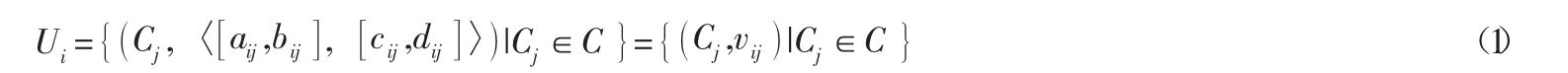
其中：cj是指不同的准则，aij≥0,cij≥0,0≤bij≤dij≤1，其中]是众筹项目pi在标准cj下的隶属函数，而是指在准则cj下项目pi的非隶属函数。在不同的准则下每一个众筹项目都可以被表达成Ui的区间直觉模糊的形式，因此我们将每一个项目和每一个准则所对应的区间直觉模糊数组合在一起就可以写出一个决策矩阵M。

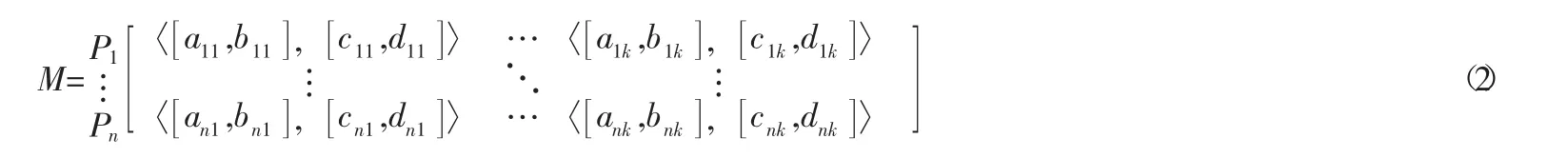
决策矩阵M的每一行表示一个众筹项目，每一列表示一个考虑准则，矩阵的每一个元素就是一个众筹项目在一个准则下的区间直觉模糊集。之后，对每一个参考准则赋予权重然后，运用权重平均的算法对每一个众筹项目基于各种准则下进行聚合，算法如下:

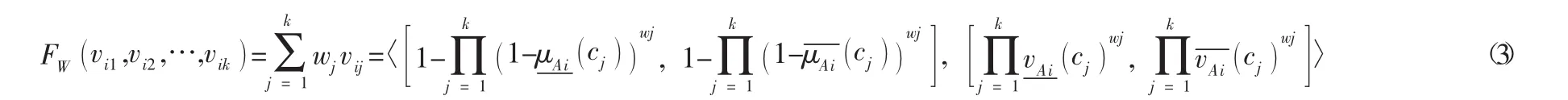
通过上面聚合算法可以把每一个参考标准都考虑到，经过计算之后可以简化前面的决策矩阵得到一个新的矩阵：

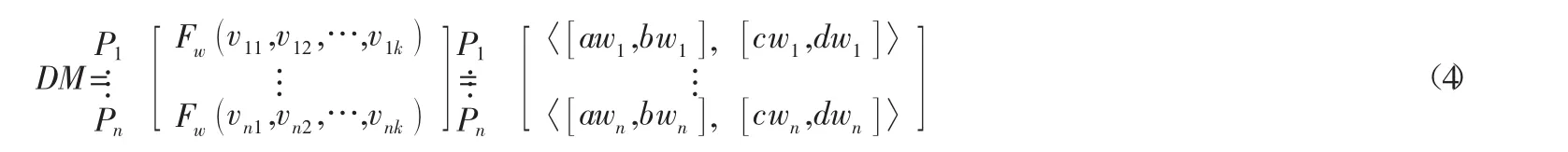
最后通过DM矩阵来计算出每一个众筹项目的区间直觉模糊值，公式如下：

2.2 多准则之间的相互扰动

扰动可以看成一个物体加入另一个物体之后产生的变化，这种变化就可以被理解为扰动。同样要考虑的是投资者在选择众筹项目的时候，所考虑的众多准则之间的相互影响。投资者在选择A和B两个众筹项目的时候如果仅仅根据距离这一参考准则选择时，假设A的地理距离比B远则投资者就会选择项目B；但如果此时投资者又同时考虑收益率这一准则，可能对选择的结果就会产生影响。项目A可能地理距离比较远但收益率高，项目B的地理距离较近但收益率低。这时投资者就要在地理距离和收益率这两个准则之间进行权衡，投资者如果注重收益率可能会选择项目A，如果更看重地理距离就会选择项目B。这就是收益率这个准则对地理距离这个准则产生的扰动影响，这些扰动之间的相互影响反应到决策的结果上就是投资者对这些参考准则的权衡比较。所以本文会提出通过计算众多准则之间的相互扰动值，把这种扰动关系表达成具体的数值，然后对所有的参考准则进行排序，最后赋予相应的权重。

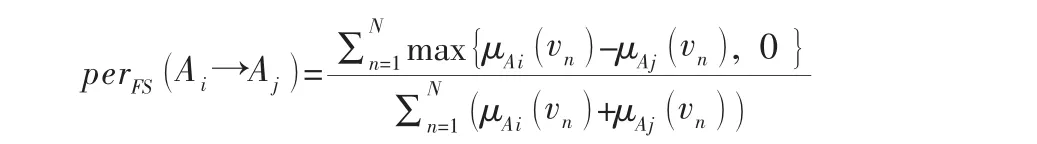
从上面的扰动表达式可以看出每一次计算都涉及两个模糊集，在投资者选择众筹项目时考虑的准则也有很多，这些参考准则并非都是独立存在的，他们之间存在相互的扰动，不同的参考准则之间的扰动也是不一样的。投资者在地理距离和收益率这两个参考准则之间可能会更看重收益率，但如果再考虑投资者的个人偏好和收益率可能又会偏向于个人偏好。针对这一现象文章采用上面的扰动表达式对每两个准则进行计算，根据计算出来的值进行排序。由于扰动是相互的，所以每两个准则之间要计算两次，例如：Ai和Aj之间的扰动大小可以通过计算perFS的值，然后进行比较决定这两个准则之间的顺序。

3 情景比较

表1 众筹产品的情况说明

3个准则表达成模糊集的形式分别为：

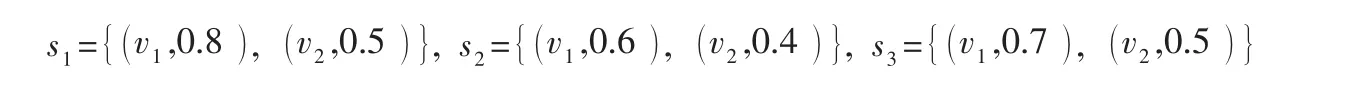
它们的决策矩阵为：

首先投资者可以通过扰动算式对3个准则进行计算。计算结果如下：

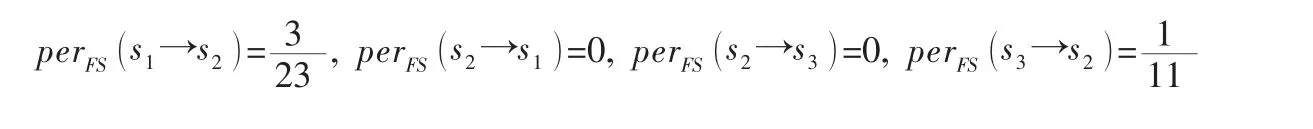
由上面的式子可以看出s1对于s2的扰动大于s2对s1的扰动，s2对s3的扰动小于s3对s2的扰动，再计算s1和s3之间的扰动即可。

通过上面的计算可以得出3个参考准则之间的扰动关系为s1＞s3＞s2，因此可以给这3个准则分别赋予权重利用上面的决策矩阵，运用相应的聚合算法可以将每一个众筹项目转变成为一个模糊区间的形式，如下面的矩阵：

然后利用公式对每一个项目进行计算：

如表2所示，情景一、情景二、情景三分别是按照类型、地理距离和投资金额作为准则对4个众筹项目进行排序的，情景四是按照本文所提的区间直觉模糊算法进行计算排序的，3个准则的权重值是随机赋值分别为情景五是按照本文所提出的扰动算法计算3个准则的扰动关系，然后据此分别赋予权重值并带入区间直觉模糊算法中。

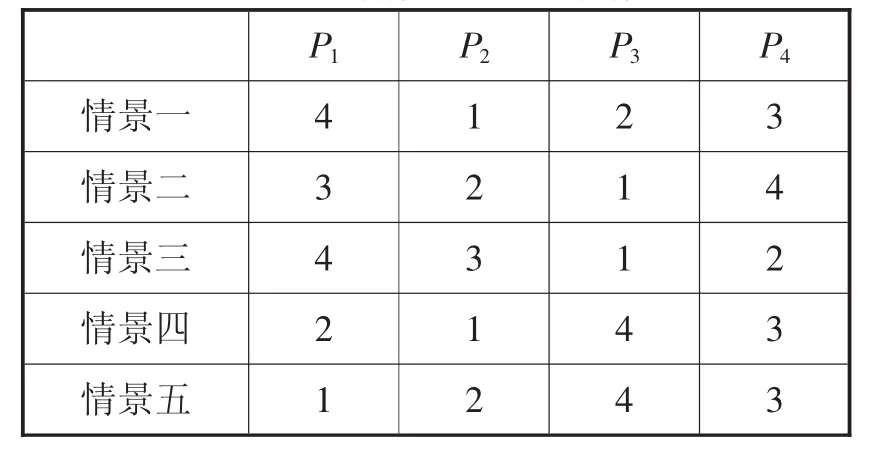
表2 五种情景下的排序情况

从表2中可以看出前3种情景得出的结果相互之间偏差较大，考虑的准则较为单一，可信度较低，后两种情景是运用区间直觉模糊算法综合考虑了多准则得出的结果，相互之间偏差较小，且情景五较情景四对权重的赋值更有说服力，所以得出的结果可信度更高。

4 总结

本文主要是研究投资者在选择众筹项目时要考虑的问题以及如何选择最适合自己的项目。在选择众筹项目时投资者考虑的因素一般不止一个，所以就出现了多标准情况下的决策问题。本文是从模糊决策的角度来解决这个问题的，因为：（1）模糊决策可以将不确定因素通过模糊数的形式转变成确定的形式；（2）通过聚合算法很好地考虑到了各个参考标准，相较于其他的决策方法更具有说服力；（3）对每一个项目的聚合值进行排序来选择出最优的项目。本文的亮点之处在于考虑到了投资者在选择项目时考虑的标准之间存在着相互扰动问题，所以本文使用扰动的算式计算出每一个标准之间的扰动大小，并将这种大小表达成具体的数值形式，最后根据这些值对这些考虑标准进行排序并赋予相应的权重带入聚合算式中。随着社会的发展众筹已经十分的火热了，随之而来的相关问题也很多，本文的主要目的就是从模糊决策的角度对多目标下的众筹项目的决策提出自己的方法。