基于ARIMA模型的电商销售预测及R语言实现

姜晓红，曹慧敏 （南京林业大学 汽车与交通工程学院，江苏 南京 210037）

0 引言

商品需求预测是企业物流管理计划的重要依据，是企业制定战略规划、生产计划、销售计划的重要举措。电子商务零售的需求相对于传统零售更加不确定，多种促销机制手段以及各种社会因素甚至季节影响，会导致商品的需求变化趋势变大，而不同商品的需求会表现不同的特点。商品预测精准度受数据规模或数量、数据汇总程度、需求稳定性、环境竞争力的影响较大。自回归滑动平均模型（Auto Regressive Moving Average Model，ARIMA）对历史数据处理效果较好，可较好地识别销售的基本变化趙势，对未来的市场需求进行有效预测。它可以用于当时间序列值变化趋势较大的情况，是短期预测中比较有效的预测方法。

Norbor Wiene和Andrei Kolmogomor在20世纪40年代提出了传统时间序列的基本理论基础。近年来，Fink和Pratt剔除时间序列分段点的重要性是在局部范围，通过判断局部与重点的设定参数决定新的重要点，将参数进行不同赋值，所得到的精度也不同[1]。Ramos P结合状态空间模型以及ARIMA模型对零售业鞋类商品进行了销售额的一步及多步预测，并对两种模型预测结果进行了精度对比及适用性对比[2]。国内学者曾海泉基于互关联后继树模型，提出时间序列挖掘与相似性查找技术[3]。侯澍旻认为可以根据当前时间序列数据挖掘的研究情况将时间序列数据挖掘定义为：将基于一个或多个时间序列的数据挖掘称为时间序列数据挖掘（Time Series Data Mining,TSDM）[4]。王志坚对我国1953年到2010年社会消费品零售总额年度数据进行ARMA建模[5]。郭慧敏、张学敏分别研究了基于R语言ARIMA模型在慢阻肺急性加重患者发病预测中的应用[6]和在猩红热分析预测中的应用[7]。ARIMA模型预测中发挥了作用，论文将进一步研究ARIMA模型预测商品未来需求量的可行性及R语言实现。

1 时间序列法及ARIMA模型

时间序列预测法是一种回归预测方法，ARIMA模型在时间序列分析中应用较多。它是估计非季节和季节平稳性的自回归综合移动平均模型。不同于一般回归模型用k个外生变量，X1,X2,…,Xk，ARIMA模型是用随机误差项以及变量Yt自身的滞后项来解释该变量。ARIMA方法在数据模式未知时就可以找到适合的模型，所以被广泛应用在经济领域。它的具体形式可表达为 ARIMA（ p,d,q ）。其中自回归阶数用p表示，差分次数用d表示，移动平均过程的阶数用q表示。如果数据不平稳，则需对数据进行处理差分，使其平稳，称作d阶差分。基本前提是过去的销售不存在趋势性，而是具备一个水平或平稳的模式。平稳性意味着数据中不存在增长或下降。换言之，需求数据围绕一个常数均值上下波动，与时间无关。利用时间曲线图很容易对平稳性进行评估。画出时间序列，如果并没有明显证据表明趋势存在，则可说明时间序列具有平稳性。若数据明显存在增长趋势或有大幅波动，则需要剔除不稳定趋势，最好的方法就是差分法，差分法是通过利用原始时间序列中每个观察值之间的差异或变化的一种方法，利用差分将数据转换成类似白噪声的具稳定性时间序列，白噪声的存在，也即意味着数据中不再存在趋势特征。一旦数据从不稳定转化为平稳状态，通过差分所生成的新数列即可取代。

2 基于ARIMA模型的实证与R语言实现

2.1 实例数据预处理

实例选用天猫超市数据，时间跨度为2014年10月1日至2015年12月27日。数据表中共有交易记录232 621条，交易记录属性31个，包括收藏情况、拍下情况、成交情况等。随机挑出一件id=100239的商品作为例子，将2014年10月10日至2015年12月20日数据作为训练集，2015年12月21日至2015年12月27日数据作为测试数据。对数据预处理，剔除该商品在畅销季节的异常值，采用插值的方法进行缺失值的补充，通过简单移动平均进行平滑化处理，导出时间序列图如图1所示。R语言代码如下：

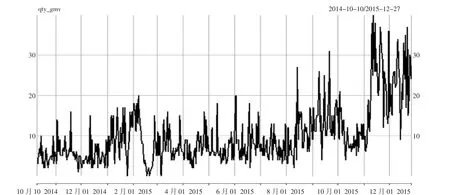
图1 剔除异常值后的商品数据时序图

2.2 原始序列平稳化及稳定性评估

通过观察时序图，可以看出该序列在不同的值附近波动，可以大致判断出该序列不是一个稳定的序列。使用R语言计算并绘出时间序列滞后所有阶数的自相关函数，如图2所示。R语言代码如下：

＞dev.new()

＞pacf(qty_gmv)

＞dev.new()

＞acf(qty_gmv)

该时间序列的自相关系数没有迅速下降到0，也没有在0处收敛，而是处于波动状态，可以判断该时间序列为一个不平稳的序列。利用R语言对数据进行根检验及白噪声检验，若白噪声存在则说明数据是平稳状态。原始时间序列自相关图如图3所示。

图2 原始时间序列偏相关图

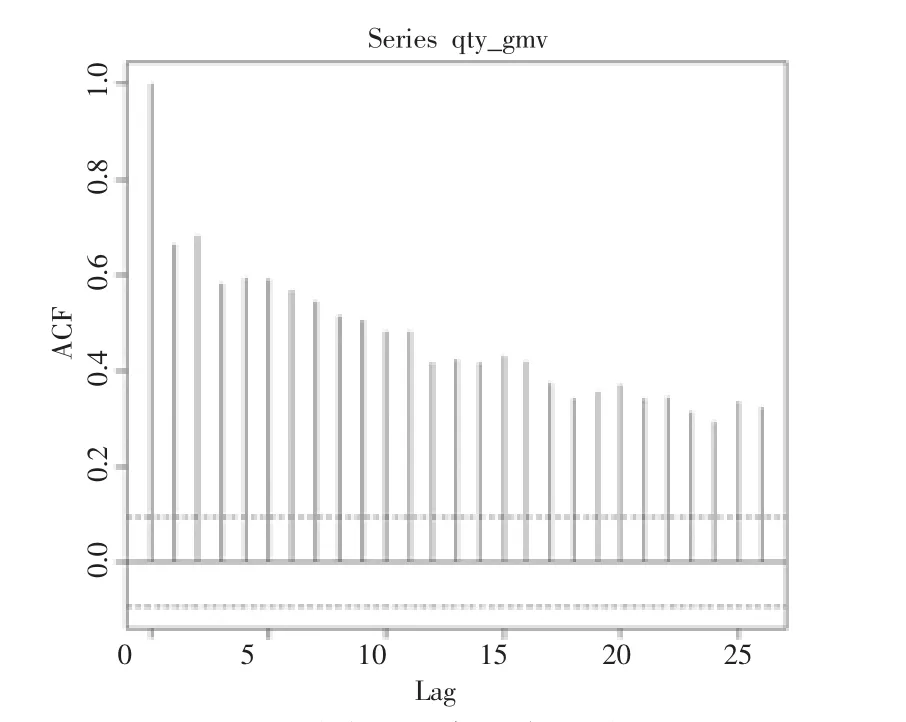
图3 原始时间序列自相关图

将原始序列进行一次差分（函数默认一阶滞后项，即lag=1），存储在dqty_gmv中。通过观察差分后的序列的折线图，显然比原始序列更平稳。对差分后的序列做ACF检验，检验结果显示序列此时是平稳的，差分一次的自相关图如图4所示，差分一次的偏相关图如图5所示。R语言代码如下：

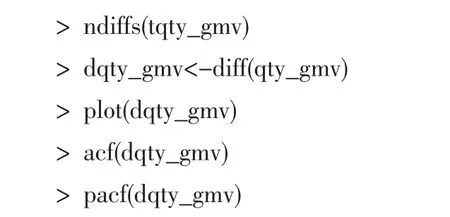
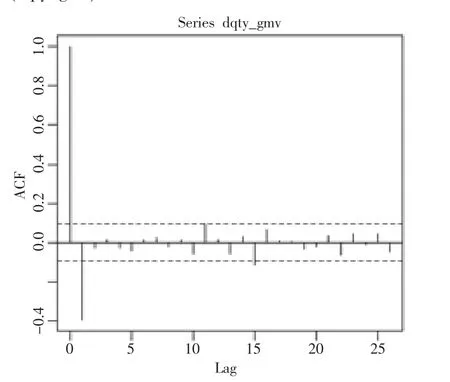
图4 差分一次的自相关图

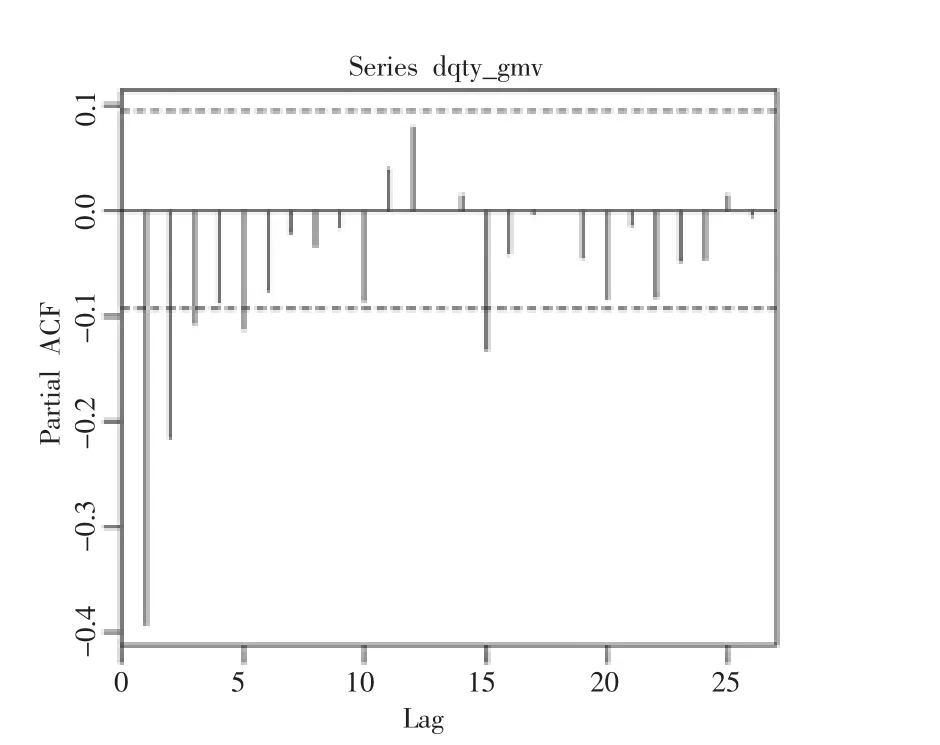
图5 差分一次的偏相关图

利用R语言urca包对数据进行单位根检验及白噪声检验，R语言代码及结果如下：

计算并绘出时间序列的所有滞后阶数的自相关函数，由时序图以及自相关函数在0处快速收敛可知一次差分后的序列为平稳序列，通过QLB的定量的检验：QLBmax，未超过显著性水平为5%时的临界值，则此时表明该序列为平稳的。与此同时，即可以得到ARIMA模型中的参数d=1。

2.3 模型判断

对于ARIMA模型而言，如果自相关系数拖尾，偏相关系数p阶截尾，则可以选用AR（p）模型；如果偏相关系数拖尾，自相关系数q阶截尾，则可以选用MA（q）模型；如果自相关系数，偏相关系数都拖尾，则可以选用ARMA（ p,q）模型。为了选择合适的ARIMA模型，引入自相关图ACF及偏相关图PACF。为了验证模型是否合适，检验模型的残差是否满足均值为0的正态分布，若满足那么对于任意的滞后阶数，残差自相关系数都应该为0。运行以下代码来检验这些假设。

qqnorm（）和qqline（）函数输出如图6所示，图中数据中的点基本落在图中的线上，显然，本例的结果还不错。用Box.test（）函数检验残差的自相关系数是否都为0。在本论文中，模型的残差没有通过显著性检验，本文可以认为残差的自相关系数为零。ARIMA模型能较好地拟合本数据。

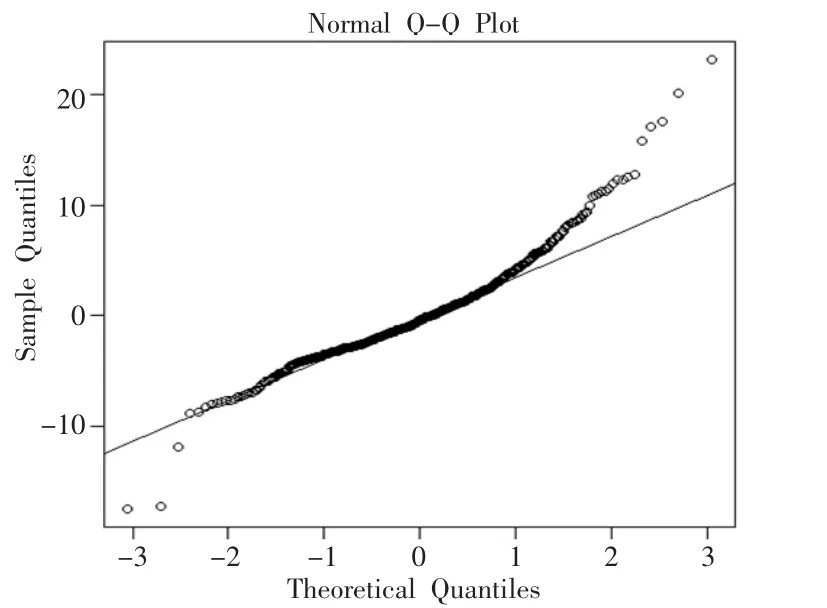
图6 正态分布QQ图

由自相关图（图7）可以看出存在超过5%的序列自相关系数超过2倍的标准差的范围，出现“自相关系数拖尾”。而序列的偏相关函数中，判断该序列的偏相关系数截尾，运用R语言的auto.arima（）函数确定p,q的值，于是设置ARIMA模型参数为arima（ 2,1,1 ）。

表1为相关系数表，其中：RMSE为均方根误差，MAE为均方根，R^2为相关性强弱。MAE值为3.443995，开方即为1.855800，表明单个记录的总体平均预测误差为1.855800，模型总体性能较好。

2.4 预测结果

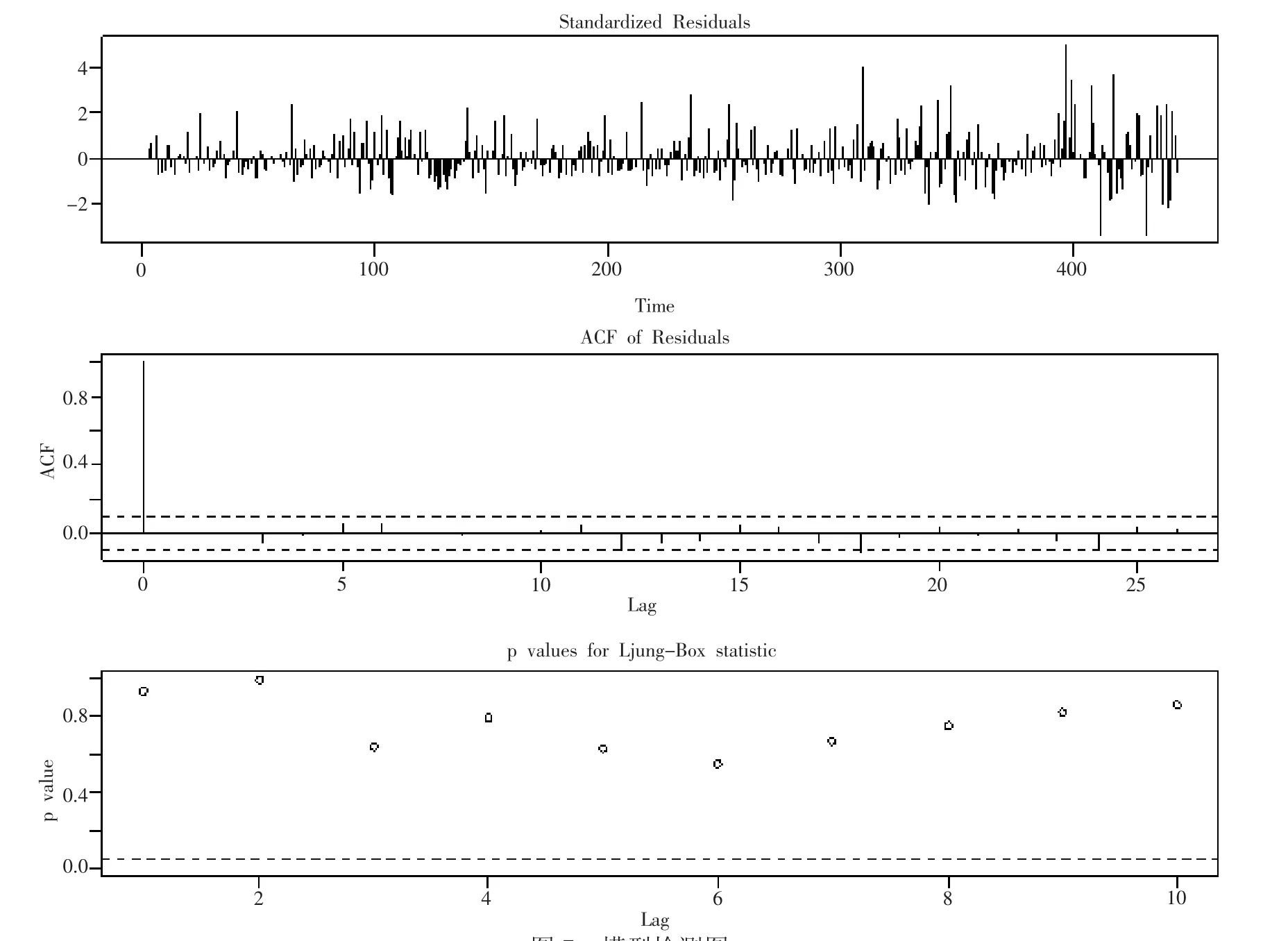
图7 模型检测图

表1 相关系数表

根据R语言forecast（）函数得到20 151 221-20 151 227一周的预测结果，并与实际销售量以及简单移动平均法预测结果对比。使用forecast程序包预测7天的销售量，R语言及结果如下：

函数选定ARIMA模型的参数为p=2、d=1和q=1。plot（）函数可以画出预测图，浅灰色和深灰色区域分别代表80%和95%的置信区间。

商品预测图如图8所示：

2.5 模型精确度验证

为了验证本方案的准确性，对另外10种商品进行ARIMA模型及简单移动平均法需求量预测，绘制基于ARIMA模型结果与简单移动预测结果的对比折线图。可以从该折线图（图9）看出，ARIMA所得到的折线图与实际值之间的拟合程度要明显大于简单移动平均所得到的折线图，即ARIMA模型的精确度较高。

3 结论

基于时间序列对大量不完整、含噪声、内容不一致的数据进行平稳化处理，采用ARIMA模型对商品需求进行预测，得到963件商品在未来7天内的全国销售量，并与简单移动平均法进行对比分析，通过统计学检验得出本方案预测结果相对精确。企业根据销售量可以以销定产，避免资源较大范围的浪费或商品供不应求的情况发生。另外，商家在淡季，尤其是旺季来临前的两个月，可以积极宣传推广产品，采取集中配货的方式以降低成本，旺季会有更好的竞争优势。本文所用模型及结果可为企业的运作和决策提供可靠依据。

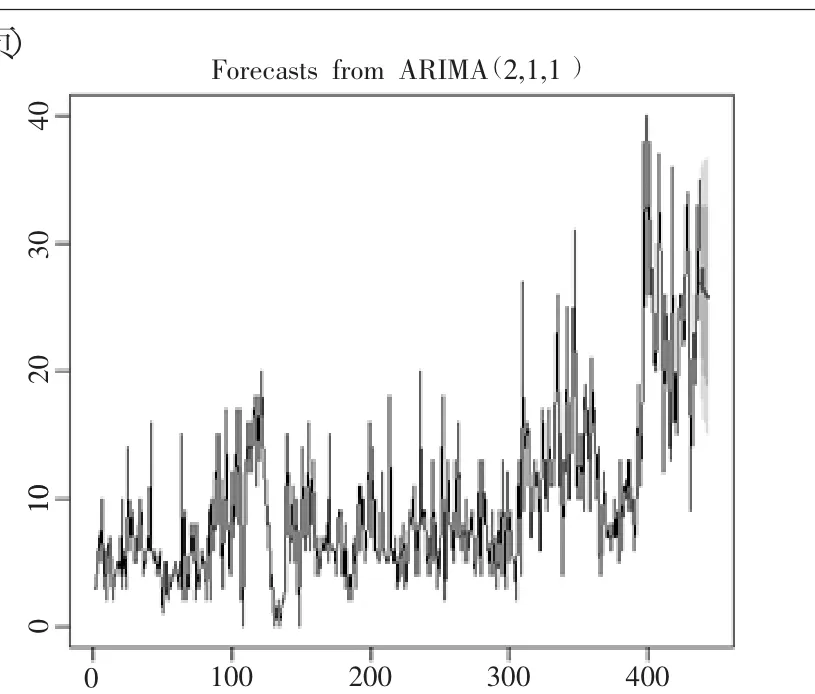
图8 商品预测图

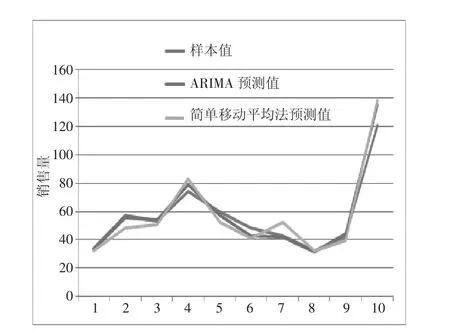
图9 ARIMA模型与简单移动平均预测对比折线图