非自治广义Birkhoff系统的组合梯度方法

董孟峰， 陈向炜

(1.苏州科技大学 数理学院，江苏 苏州 215009；2.商丘师范学院 电子电气工程学院，河南 商丘 476000)

梯度系统在研究力学系统稳定性时具有重要作用，借助梯度系统研究Birkhoff系统的稳定性是一类重要方法.梅凤翔首先介绍了两类基本梯度系统[1-2]以及Birkhoff系统的梯度表示[3-4].尚玫等提出了广义Bikhoff方程的Poisson理论[5].崔金超等给出了自治Birkhoff系统的四类梯度表示[6-7].曹秋鹏等研究了利用梯度系统研究约束自治广义Birkhoff系统的平衡稳定性[8].陈向炜等利用负定非对称的梯度系统构造稳定的广义Birkhoff系统[9].李彦敏等给出了广义Birkhoff系统的两类广义梯度表示[10].

组合梯度系统是由几类基本梯度系统组合起来构成的.利用组合梯度系统可以研究复杂力学系统的动力学性质.祖启航等给出了一类非自治Birkhoff系统的分数维梯度表示[11]，张毅给出了一类非自治Birkhoff系统的梯度表示[12]，王嘉航等给出了非自治广义Birkhoff系统的半负定矩阵梯度表示[13].陈向炜等利用组合梯度系统研究了定常Chetaev型非完整系统[14].梅凤翔等利用组合梯度系统研究了一类广义Birkhoff系统[15].目前，利用组合梯度系统研究Birkhoff系统的性质还仅限在自治的情况，本文将其推广到非自治广义Birkhoff系统来研究系统的稳定性.

1 组合梯度系统及其性质

1.1 梯度系统

梯度系统有4类基本形式.微分方程有形式

(1)

当系统为通常梯度系统时Aij为负单位矩阵；当系统为斜梯度系统时Aij为反对称矩阵；当系统为对称负定的梯度系统时Aij为对称负定矩阵；当系统为半负定的梯度系统时Aij为半负定矩阵.

1.2 组合梯度系统Ⅰ

若系统有微分方程

(2)

其中矩阵bijx=-bjix为反对称的，称为组合梯度系统Ⅰ.

(3)

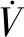
1.3 组合梯度系统Ⅱ

若系统有微分方程

(4)

其中矩阵Sijx=Sjix为对称负定的，称为组合梯度系统Ⅱ.

(5)

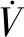
1.4 组合梯度系统Ⅲ

若系统有微分方程

(6)

其中矩阵aij=aijx为半负定的，称为组合梯度系统Ⅲ.

(7)

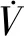
1.5 组合梯度系统Ⅳ

若系统有微分方程

(8)

其中矩阵bijx=-bjix为反对称的，Sij=Sijx为对称负定的，称为组合梯度系统Ⅳ.

(9)

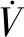
1.6 组合梯度系统Ⅴ

若系统有微分方程

(10)

其中矩阵bijx=-bjix为反对称的，aij=aijx为半负定的，称为组合梯度系统Ⅴ.

(11)

1.7 组合梯度系统Ⅵ

若系统有微分方程

(12)

其中矩阵aij=aijx为半负定的，Sij=Sijx为对称负定的，称为组合梯度系统Ⅵ.

(13)

2 非自治广义Birkhoff系统的组合梯度表示

非自治广义Birkhoff系统的微分方程为

(14)

μ,ν=1,2,…,2n

设系统非奇异，则(13)式可写为

(15)

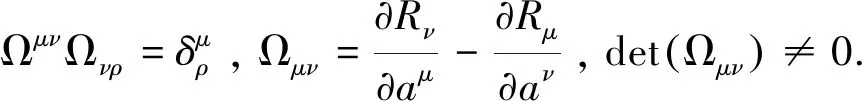
通常情况下，方程(15)不是组合梯度系统.若系统可成为组合梯度系统Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ，则存在函数V、反对称矩阵bμν、对称负定矩阵Sμν和半负定矩阵aμν分别使下列条件成立，

(16)

(17)

(18)

(19)

(20)

(21)

由于系统方程的形式不唯一，当方程的一阶形式不满足方程(16)～(21)，不能说明系统不是组合梯度系统.系统能够成为组合梯度系统，则可以找到相应矩阵和Lyapunov函数.

3 应用举例

例1广义Birkhoff系统为

R1=0,R2=a1sint,B=a1a2sint

(22)

附加项为

Λ1=3a1sint+4a2sint,Λ2=a2cost+a2sint

(23)

显然，该系统是非自治的.

由(22)式得

由方程(15)可得

上式可表示为

例2广义Birkhoff系统为

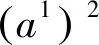
(24)

附加项为

Λ1=a1sint+5a2sint,Λ2=a1cost+a2sint

(25)

显然，该系统是非自治的.

由(24)式得

由方程(15)可得

上式可表示为

例3广义Birkhoff系统为

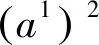
(26)

附加项为

Λ1=-2a1sint-a2cost+5a2sint,Λ2=-5a1sint+4a2sint

(27)

显然，该系统是非自治的.

由(26)式得

由方程(15)可得

上式可表示为

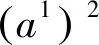
例4广义Birkhoff系统为

R1=0,R2=a1sint,B=4a1a2sint

(28)

附加项为

Λ1=4a1sint+8a2sint,Λ2=a1cost+2a2sint

(29)

显然，该系统是非自治的.

由(28)式得

由方程(15)可得

上式可表示为

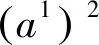
例5广义Birkhoff系统为

(30)

附加项为

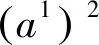
(31)

显然，该系统是非自治的.

由(30)式得

由方程(15)可得

上式可表示为

例6广义Birkhoff系统为

R1=0,R2=a1sint,B=a1a2sint-a1a2cost

(32)

附加项为

Λ1=-2a1sint+4a2sint-a2cost,Λ2=-a1sint+2a2sint

(33)

显然，该系统是非自治的.

由(32)式得

由方程(15)可得

上式可表示为

4 结 论

本文利用组合梯度系统来研究非自治广义Birkhoff系统的稳定性，通过构造Lyapunov函数直接研究系统的稳定性.这种利用组合梯度系统的性质来研究系统稳定性的方法具有普遍意义，可进一步推广到其它约束动力学系统.