深度置信网络在导弹攻击区分类中的应用*
2019-04-26杨任农张振兴房育寰左家亮张彬超
杨任农,张振兴,房育寰,左家亮,张彬超
(空军工程大学 空管领航学院, 陕西 西安 710038)
格斗导弹在现代空战中扮演着关键角色,导弹的性能可能决定空战的结果。在空战对抗过程中,空空导弹发射结果是辅助决策系统中态势评估的前提,准确地预测我方和敌方发射导弹的攻击结果,这不仅有助于评估敌方威胁、分析敌我态势,而且对我方下一步决策起到重要的引导作用。因此,探求准确预测导弹攻击结果的方法具有重要意义。
传统的空空导弹攻击区解算方法包括:一般拟合法[1]、三角变换拟合法[2]、插值法[2]等。近年来,很多专家学者针对传统方法存在的拟合精度差、收敛速度低、通用性差等问题进行了改进。张列航等[3]、王凯等[4]提出基于反向传播(Back Propagation, BP)神经网络的空空导弹攻击区解算方法,通过在线计算获得实时的、高精度的空空导弹攻击区计算结果。但模型存在输入数据不准确的问题。左家亮等[5]采用日常空战中产生的模拟发射数据,构建训练样本库,提高了训练输入数据的准确度。但实际空战输入参数态势种类多,存在简单神经网络特征提取能力不足的问题。此外,上述方法仅侧重于单纯的攻击区解算,忽视了空战对抗情况下双方攻击态势动态变化这一因素对攻击结果的影响。因此,结合机动动作,根据不同态势下预测的攻击结果对导弹攻击区进行划分,从而为飞行员和指挥人员的决策提供帮助。
近年来,以深度学习为代表的人工智能取得了巨大突破,深度学习方法取得了重要进展。而深度学习方法包含多种类型,其中深度置信网络(Deep Belief Network, DBN)具有特征提取能力强、分类效果好以及预测精度高等优点,并且其半监督学习的特点,适合于导弹攻击结果数据库规模小的现状[6]。因此,提出基于DBN的导弹攻击区分类模型,同时将传统导弹攻击区参数进一步细化,建立更加贴近实战决策的导弹攻击结果预测模型。通过对已经分类的空战数据进行训练,使用得到的模型对导弹攻击区进行分类。但是,由于DBN结构相对复杂,很难准确确定相应的网络结构。黄海波等[7]使用经验方法确定神经元数目,造成训练误差较大,预测结构不准确。潘广源等[8]提出了根据训练的重构误差确定网络结构,提高了网络模型的准确性。本文在黄海波等的基础上,使用重构误差和测试错误率作为标准确定网络训练的结构,以提高模型的准确性,并改善网络训练时间。
1 空战攻击结果分析
1.1 导弹攻击区模型
导弹攻击区是衡量导弹攻击结果的重要标准。一般包含两种:发射包线和杀伤包线[9]。其中,发射包线以被攻击目标为中心,我方飞机在该范围内向目标发射导弹,能以不低于一定概率命中目标。发射包线能够让我方获得不同方位对目标有效打击的范围,对空战决策的意义不是很大。杀伤包线是以我方飞机为中心,计算能被攻击的目标在此载机周围的最远初始位置,在空战中具有重要研究价值。因此,为了能够提供给飞行员和指挥人员重要信息,选择以攻击机为中心的导弹攻击区进行讨论。
以攻击机为中心的空空导弹攻击区主要包括远边界(超过该距离,对敌方无法造成威胁)、近边界(小于该距离,导弹无法爆炸或者载机受到威胁)和侧边界(受导弹的过载限制)。空空导弹发射区如图1所示。
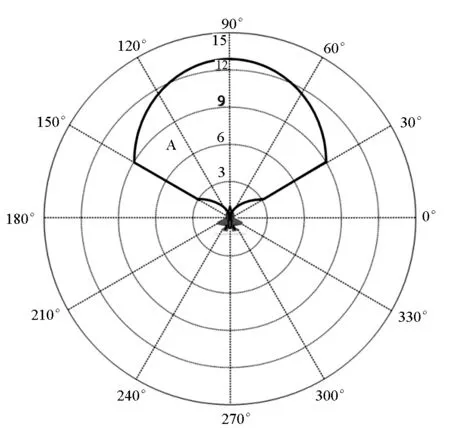
图1 空空导弹发射区示意图Fig.1 Envelop of air-to-air missile
空空导弹攻击区受多种要素的影响,包括天气、飞机高度、飞行速度、导弹性能、目标机速度、目标机高度差等,并且随着发射条件的改变而改变[10]。根据经验,导弹攻击区的远边界Rmax和近边界Rmin是高度h、速度v、机动过载n、离轴角q、进入角qT等初始攻击条件的非线性函数[11]。
(1)
其中:hA,hT表示我方高度和目标高度;vA,vT表示我方速度和目标速度;nT表示目标机动过载;q和qT表示导弹离轴角和目标进入角。
1.2 攻击区划分模型
根据实际空战情况,将导弹攻击区模型主要分成五类:①Ω1:目标做任何机动都无法躲开我方导弹攻击;②Ω2:目标需要做180°置尾机动才能躲开我方导弹攻击,而选择90°转弯机动会被导弹命中;③Ω3:目标只需要做90°机动即可躲开我方导弹攻击,如果继续按原有航线飞行则会被导弹命中;④Ω4:目标不需要做任何机动即可躲开我方导弹攻击,双方态势处于导弹攻击范围的临界状态;⑤Ω5:双方态势超出导弹攻击范围的上限,攻击有效的概率极低。由于区域Ω5的范围较大,并且对飞行员和指挥人员进行决策的帮助较小,在预测模型中不考虑区域Ω5,直接通过参数阈值判别。导弹攻击结果划分如图2所示。
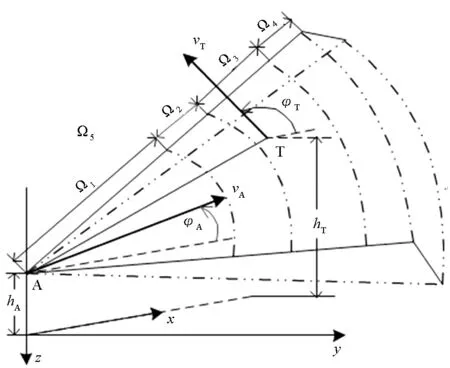
图2 导弹攻击结果划分Fig.2 Classification of missile attack results
在图2中,A为攻击机,T为目标机,目标机处于攻击机的Ω3区域内。在北东天惯性坐标系下,攻击机的坐标为(xA,yA,zA),目标机的坐标为(xT,yT,zT),攻击机高度为hA,目标机高度为hT,攻击机速度为vA,目标机速度为vT,攻击机航向角为φA,目标机航向角为φT。位置关系式为:
(2)
(3)
(4)
hA_T=hT-hA
(5)
其中:αA_T表示攻击机A攻击目标机T的水平方向视线角,dA_T表示A与T之间的距离,βA_T表示A攻击T的垂直方向视线角,hA_T表示A与T的高度差。
对攻击机而言,攻击区分类预测可理解为是对其攻击结果进行预测,区域Ω1对目标攻击结果最好;对目标机而言,攻击区分类预测可计算出空战机动区域的威胁程度,区域Ω1威胁程度最高。理论上,对区域Ω1、区域Ω2、区域Ω3、区域Ω4和区域Ω5只能进行大概的估算,无法实现十分精准的分类。由于攻击区分类模型涉及参数多,数据库较大,将采用深度学习算法学习双机在不同态势下的空战结果的数据,进而实现相对准确的攻击区划分。
2 基于DBN的导弹攻击结果预测模型
2.1 空战攻击结果预测模型
在超视距空战中,影响导弹攻击结果的态势参数主要包括:hA,hT,dA_T,vT,αA_T,βA_T,φA和φT。基于此,建立攻击机与目标机之间的态势参数与导弹攻击结果的关系,DBN导弹攻击区分类模型如图3所示。
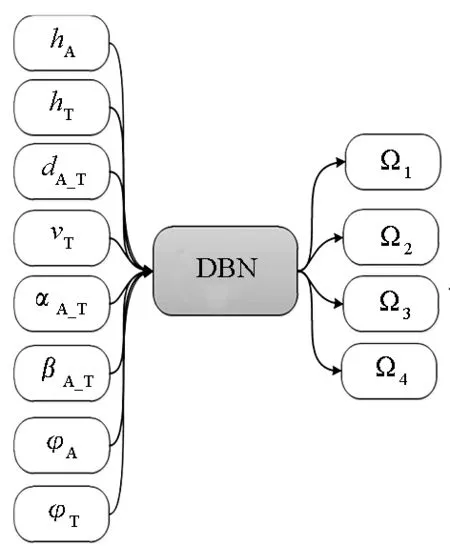
图3 基于DBN的导弹攻击结果预测模型Fig.3 DBN-based missile attack results prediction model
2.2 深度置信网络模型
DBN虽然是一种有监督的深度学习方法,但是由于其内部是由一系列叠加的受限玻尔兹曼机(Restricted Boltzmann Machines, RBM)和BP神经网络构成,兼具无监督学习方法的优势,其网络结构如图4所示。
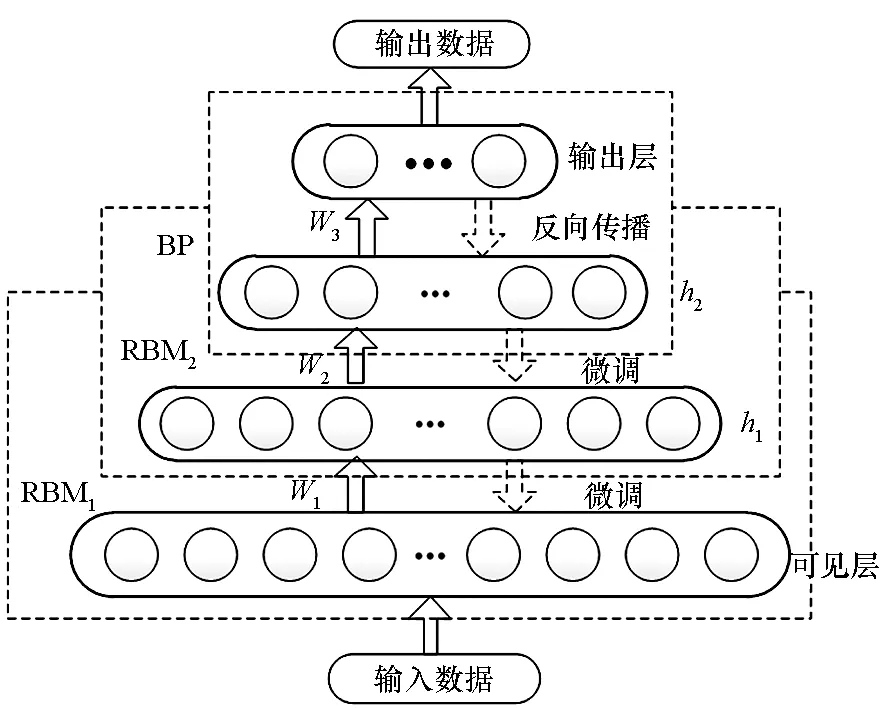
图4 DBN结构图Fig.4 Structure of DBN
在图4中,第一层是可见层,接收输入数据,输入数据经过隐含层h1和h2由输出层输出。Wi表示层间权值。
DBN主要使用“逐层贪婪[12]”的方法进行训练,处理流程为:①RBM使用无监督方法进行训练,并且每一层RBM需要单独进行训练,尽量保证特征信息被保留,前一层RBM的输出作为后一层RBM的输入;②无监督训练后输出到BP神经网络中,使用有监督方法训练网络,并采用反向传播算法调整网络参数。
在DBN中,RBM起到十分重要的作用,其结构如图5所示。
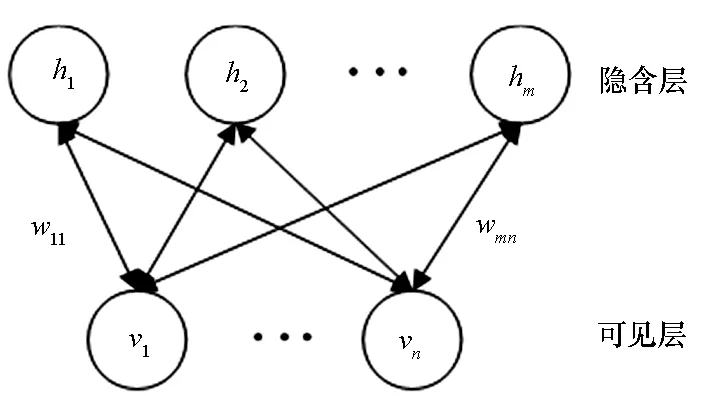
图5 RBM网络结构图Fig.5 Structure of RBM network
由图5可知,RBM由可见层和隐含层组成,wij表示可视层和隐含层之间的权值。
重构误差RError为RBM的重构特征与原始数据的误差,表达式为:
(6)
式中:n表示样本个数,m表示样本维度,pij表示经过Gibbs采样重构的新特征,dij表示训练数据,pb表示取值个数或范围。
2.3 数据采集与训练样本库构建
根据日常空战中产生的模拟发射数据,将不同态势下导弹发射时刻的攻击机与目标机相对态势数据作为模型输入,具体为2.1节的八种特征参数。根据文献[13]提出的弹道仿真理论,精确计算在该态势下的攻击结果,并按照结果进行分类,具体有Ω1、Ω2、Ω3、Ω4四种。
结合导弹性能的约束条件对数据采集进行如下定义:
(7)
采集的数据必须满足式(7),在此基础上,将态势数据输入到弹道仿真模型中,计算攻击结果。空战攻击结果如图6所示,通过为目标机选择不同机动动作,实现导弹攻击结果的进一步划分。
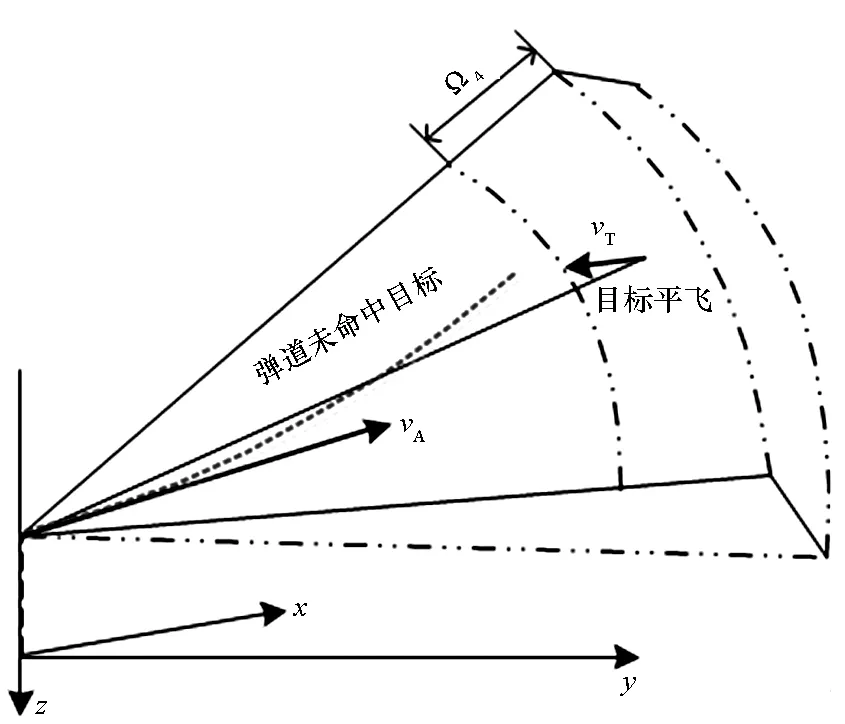
(a) Ω4
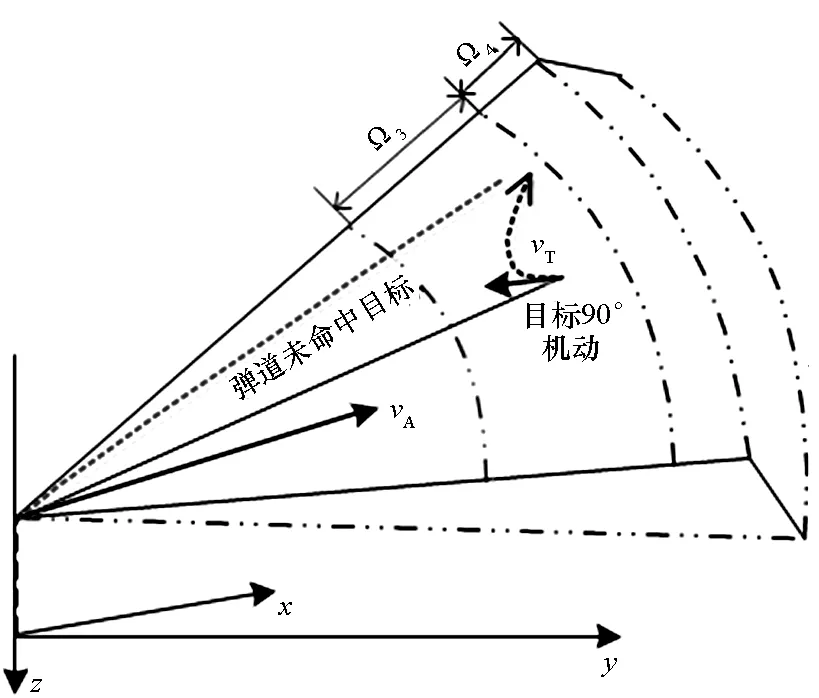
(b) Ω3
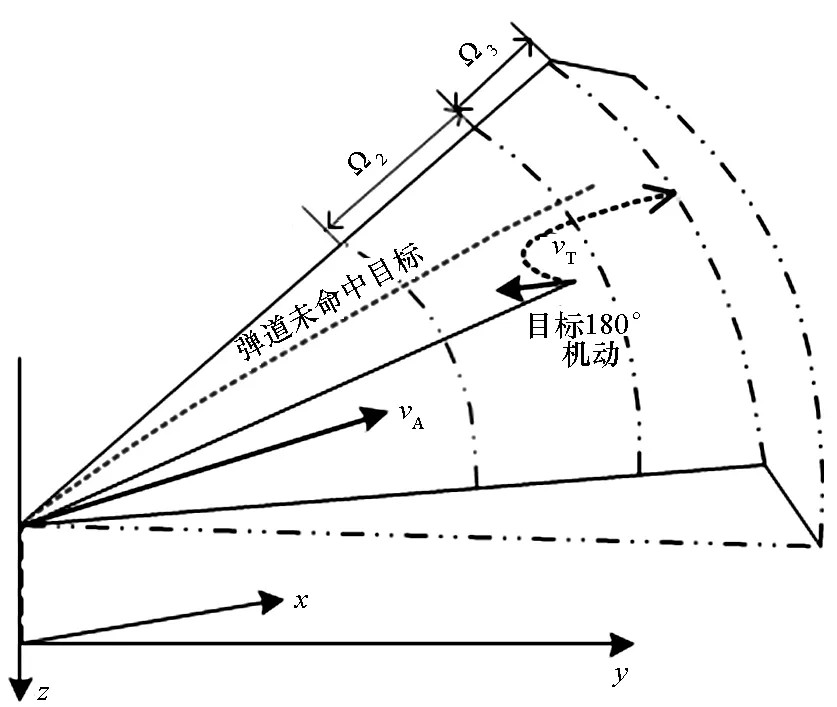
(c) Ω2
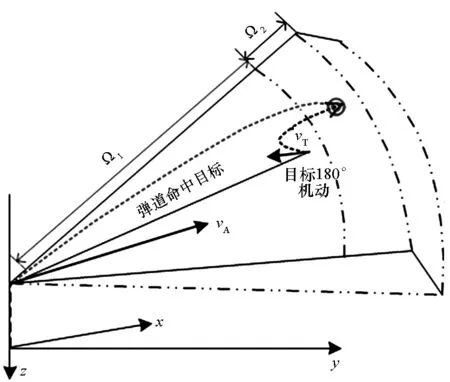
(d) Ω1图6 空战攻击结果分类Fig.6 Classification of missile attack results
具体步骤如下:
Step1:在目标不做任何机动平飞时,仿真弹道没有命中目标则属于Ω4。
Step2:如果Step 1命中,则在此态势下目标机做90°机动,重新进行弹道仿真,仿真弹道没有命中目标且不属于Ω4的区域,则属于Ω3。
Step3:如果Step 2命中,则在此态势下目标机做180°机动,重新进行弹道仿真,仿真弹道命中目标的区域属于Ω1,没有命中且不属于Ω3的区域则属于Ω2。
通过上述步骤,完成Ω1、Ω2、Ω3和Ω4的空战攻击结果数据分类标记。使用弹道仿真方法代替专家人为地进行烦琐且需要大量时间的数据样本分类标记工作,有效地避免了数据标记中的人为主动因素,实现对区域Ω1、Ω2、Ω3和Ω4数据样本的客观分类。
由于攻击机和目标机的高度、速度都是动态变化的,假设按此标准对攻击机的攻击区域进行样本空间拟合,数据量将会相当大。为使训练样本尽可能多地包含空间态势种类,保证训练数据库的完整性,同时考虑实际空战中,攻击机与目标机相互牵制,因此,选择相对态势数据进行拟合。此外,考虑导弹攻击效果与导弹高度的关系,数据采样在高度范围内进行。
3 模型建立与参数训练
从获得的导弹攻击区分类样本库中选取样本,构建DBN导弹攻击区分类模型的训练样本集(Xtrain,Ytrain)和测试样本集(Xtest,Ytest)。其中,Xtrain为样本库中随机抽取的50 000组数据,Xtest为样本库中随机抽取的10 000组数据,Ytrain和Ytest分别为每组数据对应的导弹攻击区分类结果。
3.1 DBN模型隐含层数的确定
由文献[14]可得,DBN隐含层数和网络重构误差以及模型精度的关系如下:
1) DBN隐含层数目越多,提取输入数据特征的能力越好;
2)网络的重构误差体现了模型对数据的训练程度,重构误差越小,说明训练好的模型越接近训练数据模型;
3)DBN采用的梯度下降法会使训练误差随隐含层数的增加而增大,层数越多,训练难度越大;
4)随着网络层数的增加,训练成本会急剧增大。
由此可知,DBN隐含层数的选择对于模型的准确性具有重要意义,既要保证模型精度,又要降低训练成本和缩短训练时间。在引入重构误差RError的基础上,加入测试错误率Error。测试错误率Error是指从导弹攻击区分类库中抽取一定量样本进行测试时,模型判别错误的样本数占总测试样本数的比率。隐含层数的确定公式为:
(8)
其中:ω表示设定的目标重构误差,ζ表示设定的目标精度,L表示DBN隐含层数,Nrbm表示RBM隐含层数。整个训练过程是:DBN首先进行无监督训练,如果RError小于或等于设定值,进行下一步的反向微调和数据测试;如果RError大于设定值,将隐含层数加1,重新进行无监督训练,直到RError小于或等于设定值。然后进行反向微调与数据测试,并判断Error是否小于或等于设定值;如果Error大于设定值,将隐含层数加1,重新进行训练,直到Error小于或等于设定值,进而确定隐含层数。DBN的训练流程如图7所示。
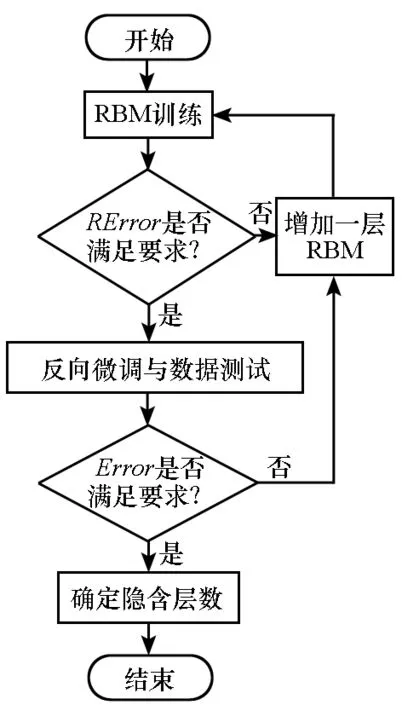
图7 DBN隐含层数确定流程图Fig.7 Determination flow chart of DBN hidden layers
从训练集中抽取7000组数据进行训练和测试,其中,5000组数据用于无监督训练,并且分成50个批次,每个批次100组数据;1000组数据用于有监督训练;1000组数据用于错误率测试。每个隐含层默认神经元为100个,根据样本实际训练情况和文献[9]关于误差阈值的确定方法,将重构误差条件设定为RError≤15%,模型测试错误率Error≤13%。考虑到重构误差和分类误差阈值的确定具有一定的主观性,为了检验得到的隐含层数是否最优,在确定最优隐含层数后,增加1组隐含层数为最优隐含层数加1的实验。通过实验,共得到4组不同隐含层数的训练结果,结果如图8和表1所示。
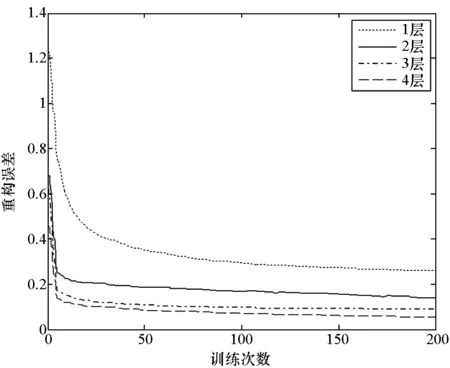
图8 不同层数重构误差图Fig.8 Reconstruction error of different layers
由图8可知,DBN网络的重构误差随着网络层数的增加而减小,并且隐含层数为3和4的重构误差相差较小。
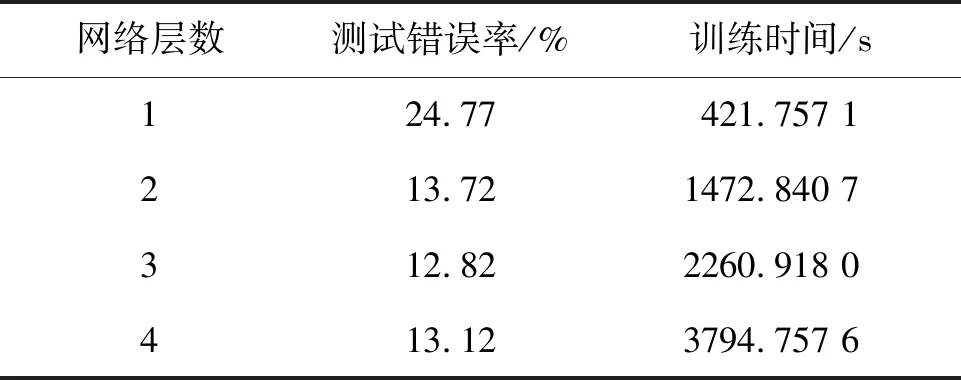
表1 不同层数的训练结果
由表1可知,测试错误率随着网络层数的增加先减小后增大,并且当网络层数为3时达到最小值。训练时间随网络层数的增加而延长,符合预期效果。这说明层数的增加导致反向梯度下降算法的误差累加过大,测试错误率不随着网络层数的增加而一直减小。由此确定DBN最优网络隐含层数为3。
3.2 网络各层节点数的确定
隐含层神经元数目的确定目前还没有统一的方法或者经验公式[15]。由问题可知,输入层神经元个数nv=8,输出层神经元个数no=4,最优隐含层数为3。考虑到隐含层神经元反映了导弹攻击区模型,并且可以通过降低隐含层神经元数目提取数据特征,将隐含层神经元数目设置为nh1=100,nh2=80。由于最后一层隐含层神经元数目直接关系到模型最终的准确率,采用类似穷举的方法确定nh3的值,其中,nh3∈[10,60],步长取2。最后,根据每次得到的重构误差和测试错误率确定最优神经元数目,仿真结果如图9和图10所示。
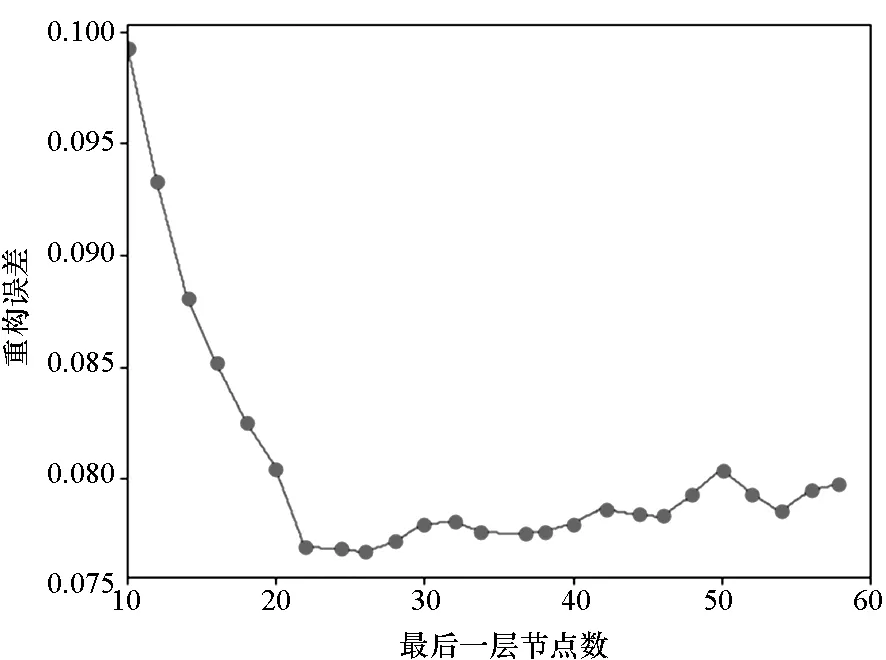
图9 最后一层训练重构误差Fig.9 Reconstruction error of the last layer
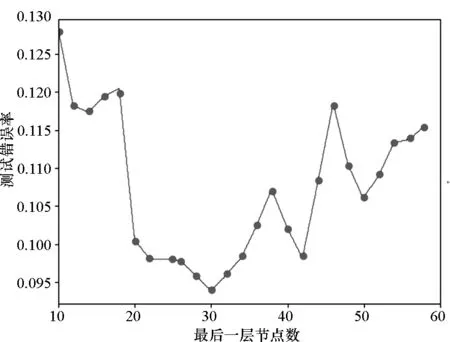
图10 最后一层测试错误率Fig.10 Test error rate of the last layers
由图9和图10可知,当最后一层节点数目大于22时,重构误差几乎保持不变;当最后一层节点数目为30时,测试错误率最低。因此,选取最后一层神经元数目为30。
由此可得,最终建立的DBN结构为8-100-80-30-4。
3.3 DBN参数设置
在进行DBN训练之前,需要设置模型参数,主要参数如下:
1)学习率。根据专家经验,设置权重学习率lw=0.050,可见层偏置学习率lbv=0.100,隐含层偏置学习率lbh=0.100。为了避免算法陷入局部最优值,引入动量项。动量更新公式为:
(9)
式中:K表示动量项,θ表示网络参数集,Wij表示节点间的权重,t表示迭代次数。
2)初始权值和阈值。随机初始化权值服从N~(0,0.1)的正态分布,输入层和隐含层阈值设置为0。
3)Batchsize。为了提高运算效率,将训练集分成包含100个数据的小批量数据,设置Batchsize为100。
4)微调次数。微调次数决定模型精度,为了获得较优的微调次数,分别求出不同微调次数对应的测试错误率。不同微调次数的训练结果如图11所示。由图11可知,当微调次数达到396时,错误率基本保持不变,并且满足要求。因此,设置微调次数为400。
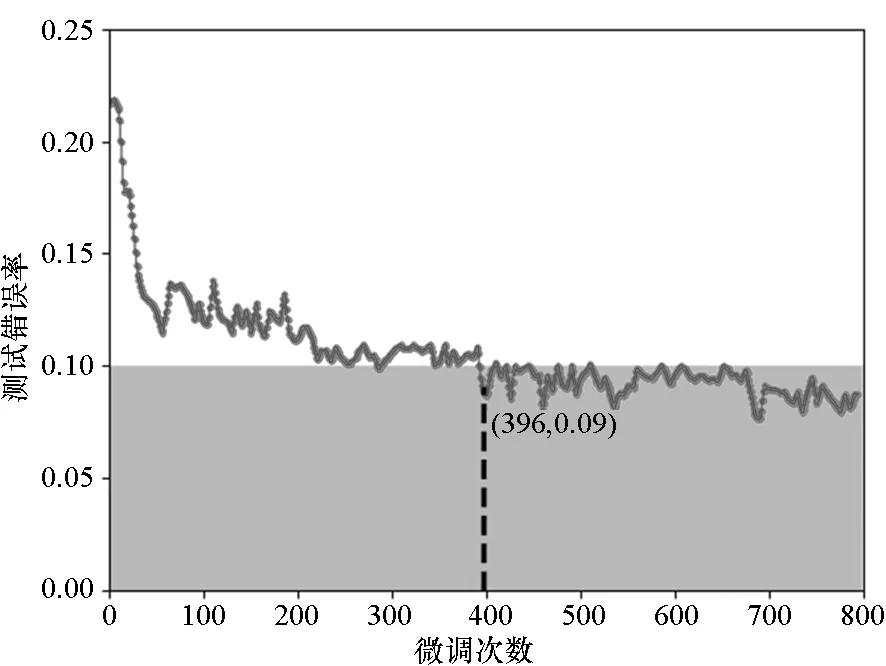
图11 不同微调次数错误率Fig.11 Error rate of different fine-tuning times
4 实验结果与分析
软件平台为TensorFlow平台,硬件平台为具有12 Inter Xeon(R) E5 CPU和4 GB RAM的高性能处理器。
4.1 网络参数特征分析
DBN模型最终结构为8-100-80-30-4,通过训练样本集(Xtrain,Ytrain)和测试样本集(Xtest,Ytest)对模型进行训练和测试。使用训练好的多层DBN对10 000组测试数据进行分类,其中用于微调的400组数据进行训练集正确率的验证,而其余9600组数据则进行测试集正确率的验证。模型训练完成后,逐层提取经过网络后的原始数据特征值,得到特征提取线,如图12所示,图中纵坐标为原始数据和各隐含层重构特征,横坐标对应四种区域。
由图12可得:四类导弹攻击区具有不同的特征提取线,并且差异较大;根据特征提取曲线可知,导弹攻击区的特征被逐层提取,并且特征数量越来越少。
4.2 微调数据采样方式讨论
在对模型进行微调的过程中,选择样本库数据进行有监督学习称为微调数据采样。微调数据采样方式的不同对于训练效率和模型精度的影响也不同。因此,采用边界采样、等间距采样和随机采样三种方法进行有监督学习。边界采样即提取该区域边缘的数据进行有监督学习,等间距采样即在样本库中等间距选取数据,随机采样即在样本库中随机选取数据。具体采样方式如图13所示。
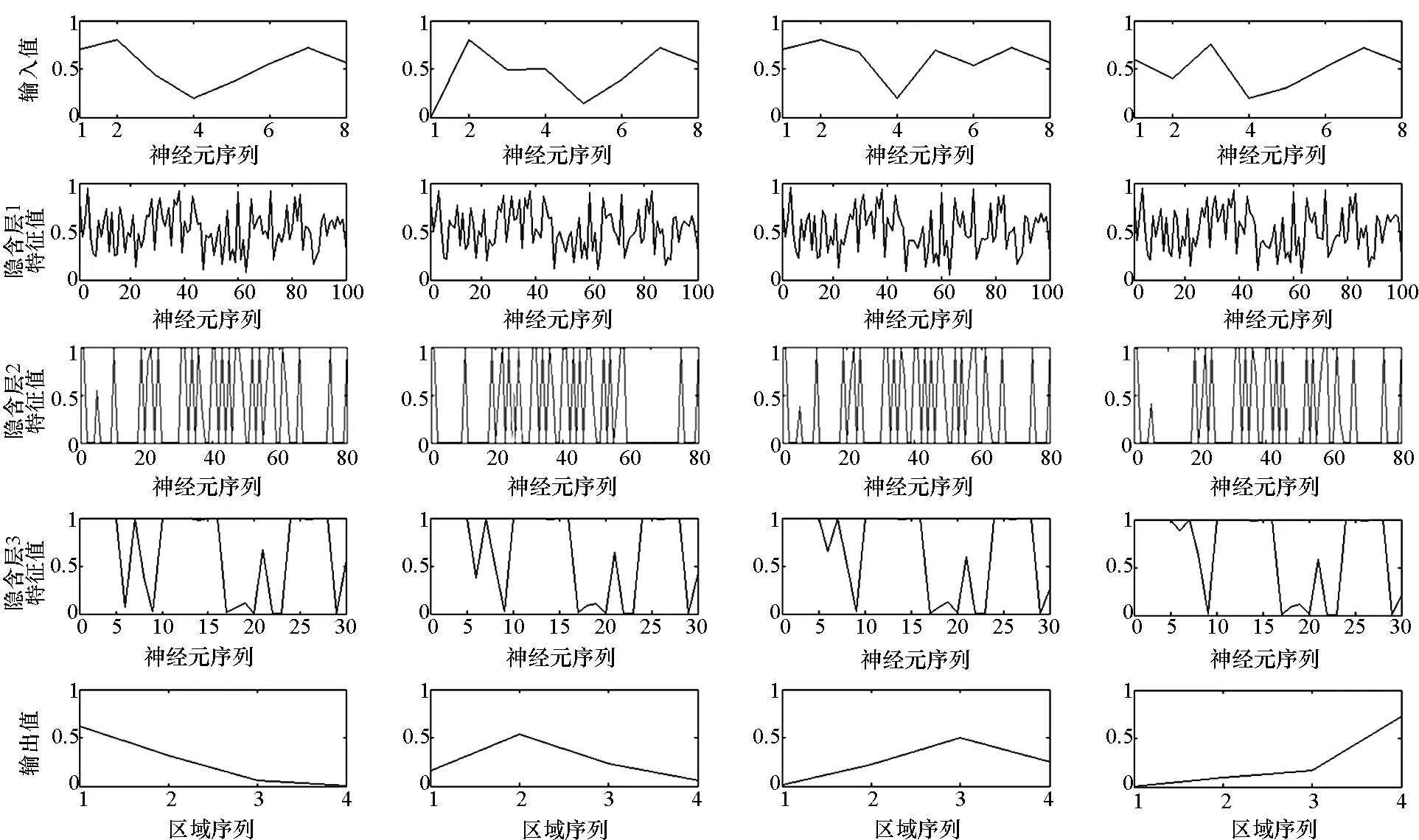
图12 逐层特征提取线Fig.12 Curves of feature extraction layer by layer
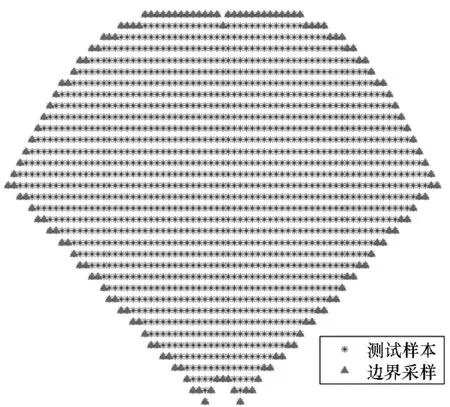
(a) 边界采样 (a) Edge sampling
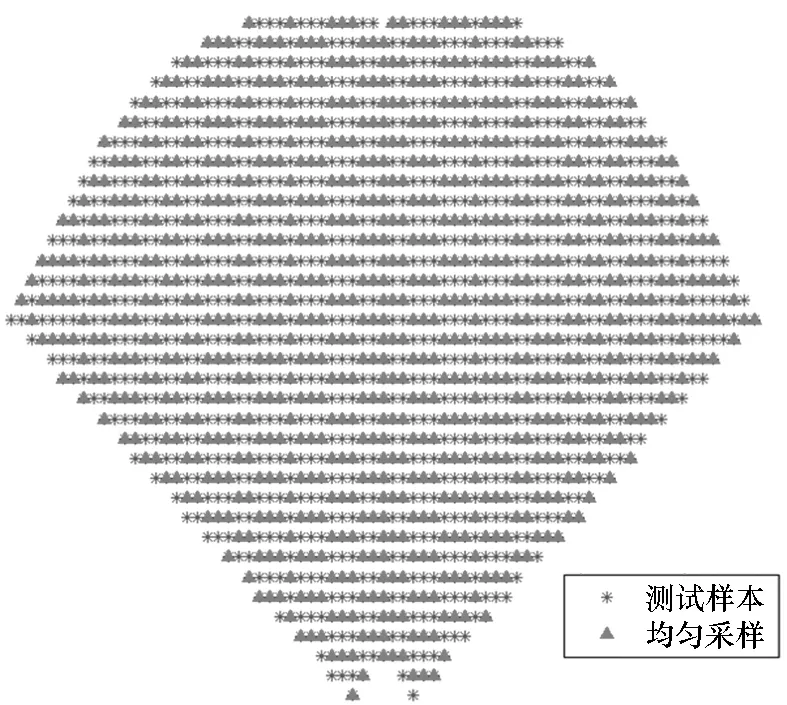
(b) 等间距采样 (b) Uniformly sampling图13 两种采样形式Fig.13 Two sample formations
在保证模型预测精度的基础上,分别使用三种采样方式训练DBN,将测试集正确率标准定为85%,测试三种方法达到准确率要求所需要的采样数量,微调训练时间和在该采样方式下最终的正确率,实验结果如表2所示。
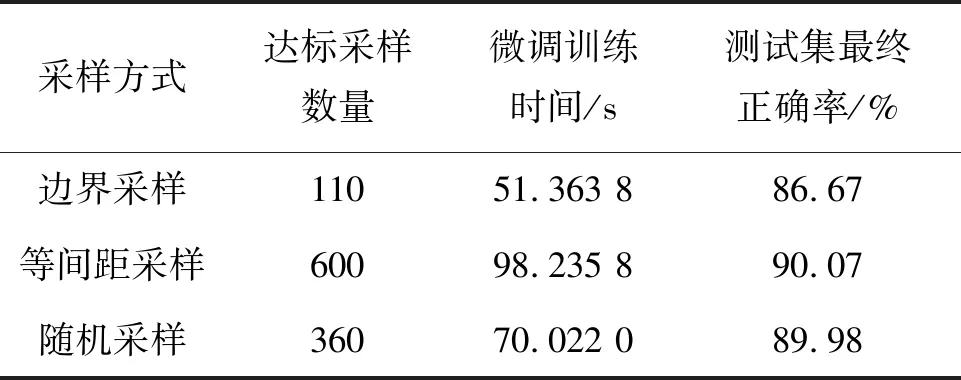
表2 三种样本采样方式效果对比
由表2可知,边界采样在采样数量较少时就可以达到较高水平,但最终模型的正确率上限较低,样本的选取也需要对样本库进行操作;等间距采样数量最多,微调训练时间最长,最终达到的正确率上限也最高;随机采样数量适中,最终达到的正确率上限也较高。综上,在实际应用中,随机采样适用性更强,等间距采样和边界采样对样本数据操作更方便。
4.3 分类有效性检验
为检验DBN的准确性,分别使用BP神经网络(网络结构8-90-4)和支持向量机(Support Vector Machine, SVM)(径向基核函数,惩罚因子c=4,核函数参数g=2.5)两种方法进行对比分析,三种算法的分类结果如表3所示。
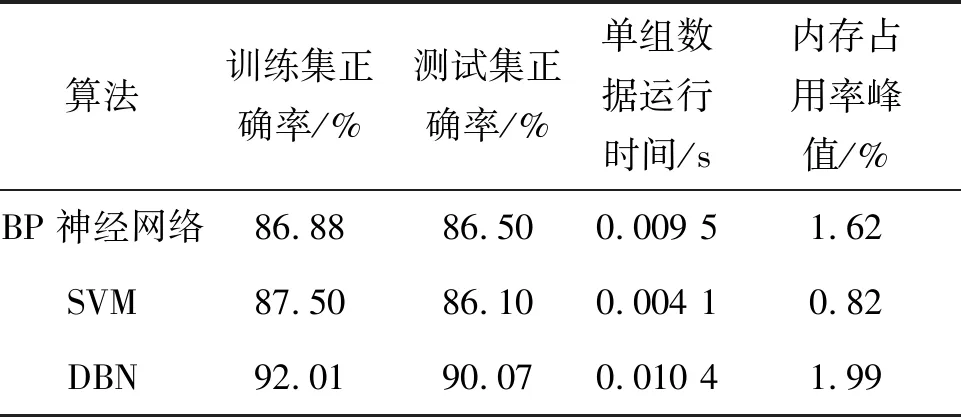
表3 三种算法分类结果对比表
由表3可知,DBN的正确率高于BP神经网络和SVM。经过分析,输入数据的维数较高,数据量大,参数变化范围广,而BP神经网络规模小,特征提取能力差,SVM训练成本随着样本量的增加急剧增大,惩罚因子等参数难以确定,两种方法均难以提取态势信息与导弹攻击结果关系的主要特征信息,导致分类正确率不高。而DBN通过深层的网络结构,建立了从原始输入到抽象特征的良好映射关系,从而有效地对导弹攻击结果进行分类。
从处理测试集的运行时间和内存占用率峰值两方面性能评价三种算法:BP神经网络和DBN隐含层数目较多,运行时间较长,占用内存多,但是,训练好的DBN和BP神经网络模型的单组运行时间均满足实时性要求,并且DBN的准确性最高,具有实际应用价值。
5 结论
本文提出了基于DBN的空空导弹攻击区分类模型。构建了导弹攻击结果的样本数据库。根据目标机动方式的不同,结合导弹攻击结果将导弹攻击区分为五个部分。其次根据重构误差和测试误差率确定DBN网络拓扑结构,从而完成攻击结果的预测。然后在实验部分搭建TensorFlow仿真平台,通过模拟导弹发射过程构建训练样本库,讨论了采样方式的不同对模型结果的影响。最后与BP神经网络和SVM进行分类对比实验,验证了模型的有效性。使用TensorFlow平台实现导弹攻击区分类,主要用于仿真实验部分,在工程实践部分,需要进一步探索实现算法和软件平台。
