基于神经网络的糖尿病多种并发症
2019-04-26白旭飞
文/白旭飞
目前我国糖尿病等慢性病患者人数居世界首位,临床研究显示,随着糖尿病发病率的上升,糖尿病的相关多种并发症已经成为人类致死主要的原因,因此糖尿病多种并发症的研究有重要意义。糖尿病多种并发症研究,其目的为找寻糖尿病较为高发的多种并发症,并进一步找寻对应的哪些因素影响较大,是因果挖掘在辅助医疗方面的尝试。糖尿病多种并发症始于1977年,RobertTurner等人建立的第一个单一因素(血糖)KUPDSModels预测糖模型是世界首个相关模型。虽然多种并发症模型发展较早,但是在中国该方法还处于起步阶段。李戈等通过logistic回归筛选变量并采用神经网络建立多种并发症,在非神经多种并发症中研究较好;白云静等将中医方法与神经网络相结合运用在糖尿病肾病研究方面得到比较全面的诊断能力;宋鹤兰等人通过神经网络预测糖尿病胎儿的体重。
然而,目前研究仍然处于探索阶段,大体分为两个方向:糖尿病单一多种并发症研究;糖尿病多种并发症研究。单一多种并发症研究相对发展较好,预测精确较高;而多种并发症研究还没有较好的方式方法。基于此,本文结合神经网络的优点,提出了基于神经网络的糖尿病多种并发症分析方法,并开展了相关的实验和分析。
1 数据预处理与并发症选择
1.1 数据预处理
本资源来自与国家临床医学科学数据中心(301医院)提供的“糖尿病数据”,采用全血糖化血红蛋白测定(简称糖化)334条记录、尿常规测定(简称尿常规)310条记录、生化测定(简称生化)条记录三项数据集合,并将无关项如就诊时间等删除。参考联合国世界卫生组织糖尿病血糖诊断标准、中国国家统计局《中国成人血脂异常防治指南》和数据中的诊断结果等标准,并结合部分医院建议。本文对指标进行了赋值,其指标选择和评判标准如表1所示经过简化(不区分1,2型糖尿病),糖化有效项为3项,尿常规有效项为14项,生化有效项为24项,其数据集合详细信息如表1,2,3所示(由于篇幅关系,仅展示部分)。

表1:全血糖化血红蛋白测定3项指标

表2:尿常规测定14项指标(部分)

表3:生化测定24项指标(部分)

表4:主要多种并发症分布

表5:KMO 和 Bartlett 的检验(生化)

表6:KMO 和 Bartlett 的检验(尿常规)
通过3个表可知,不同因素之间的量纲往往不同。比如镁(mmol/L)和尿蛋白定性试验(mg/dl)的单位差距极大。因此为解决量纲问题,本文采用Z-Score标准化处理数据,其公式为:

该公式中 为原始数据的标准差,σ为总体平均值,μ为某一个体的值。通过该方法,可以在数据大小关系的情况下,将有量纲的值转换为无量纲的值,方便不同量纲值之间的比较和运算。
1.2 并发症选择
由于糖尿病并发症众多,选择哪些并发症作为模型的研究将决定研究的价值所在。本文中,对于多种并发症的确定,直接来源于数据中的“诊断”项。该数据经过统计发现肾病114例占10.52%(肾病综合征36例占%3.32和慢性肾功能不全78例占7.20%)、高血压94例占8.67%和冠心病90例占8.30%是糖尿病的主要多种并发症。表4对主要的多种并发症的数量和占比(占比大于2%的因素)进行了详细的表示。
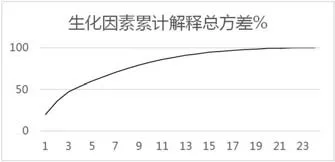
图1:生化因素累计解释总方差%
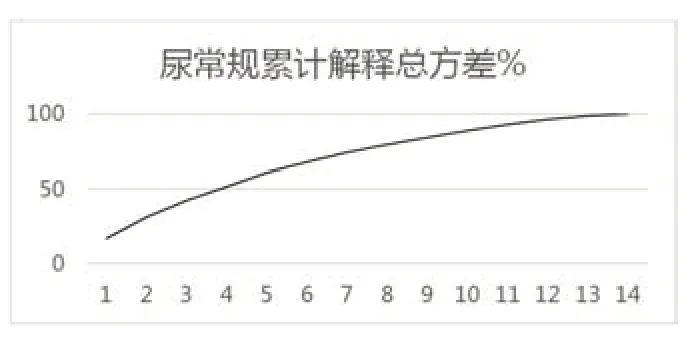
图2:尿常规因素累计解释总方差%
经过统计,发现并发症多集中于前五(占34.90%),因此本文中并发症选择了肾病、高血压、冠心病、糖尿病酮症、重症肺炎五个相关并发症,进行下一步研究。
2 并发症主成分因素分析
在研究建立模型之前,由于数据的因素量过多,模型的复杂度和耗时都会过高。并且糖尿病并发症的多个因素之间往往有一定相关性,因此采用主成分因素分析,删除因素中紧密相关的冗余项删除,在保持因素信息不变的情况下减少因素数量,降低模型复杂度。
2.1 KMO和Bartlett球形检验
在主成分前,先要进行相关判断,检验相关因素能否进行主成分因素分析。本文采用常见的KMO和Bartlett球形检验。KMO检验用于检查变量间的相关性和偏相关性,取值在0~1之间,KMO统计量越接近于1,变量间的相关性越强,偏相关性越弱,因子分析的效果越好;Bartlett球形检验判断如果相关阵是单位阵,则各变量独立因子分析法无效,其结果越接近0分析越可行。对因素较多的尿常规和生化两项进行检验,可以得到表5、表6。
该表格中第一行值表示KMO值,最后一行值表示Bartlett球形检验值。通过图表可知,生化和尿常规的KMO值均大于50%,且Bartlett球形检验小于40%,适合进行因子分析。
2.2 主成分分析结果
经过比对,分别将生化和尿常规分类为11项和10项,其解释总方差(包含原始信息的百分百)如图1、图2。
如图2、图3所示,随着因素的增加,累计解释总方差不断增加,一般取85%以上较为合适。因此这里分别选择11项生化和10项尿常规因素,他们的解释总方差分别为85.795%和88.767%。经过因素分析得到如下结果(表7、表8)。
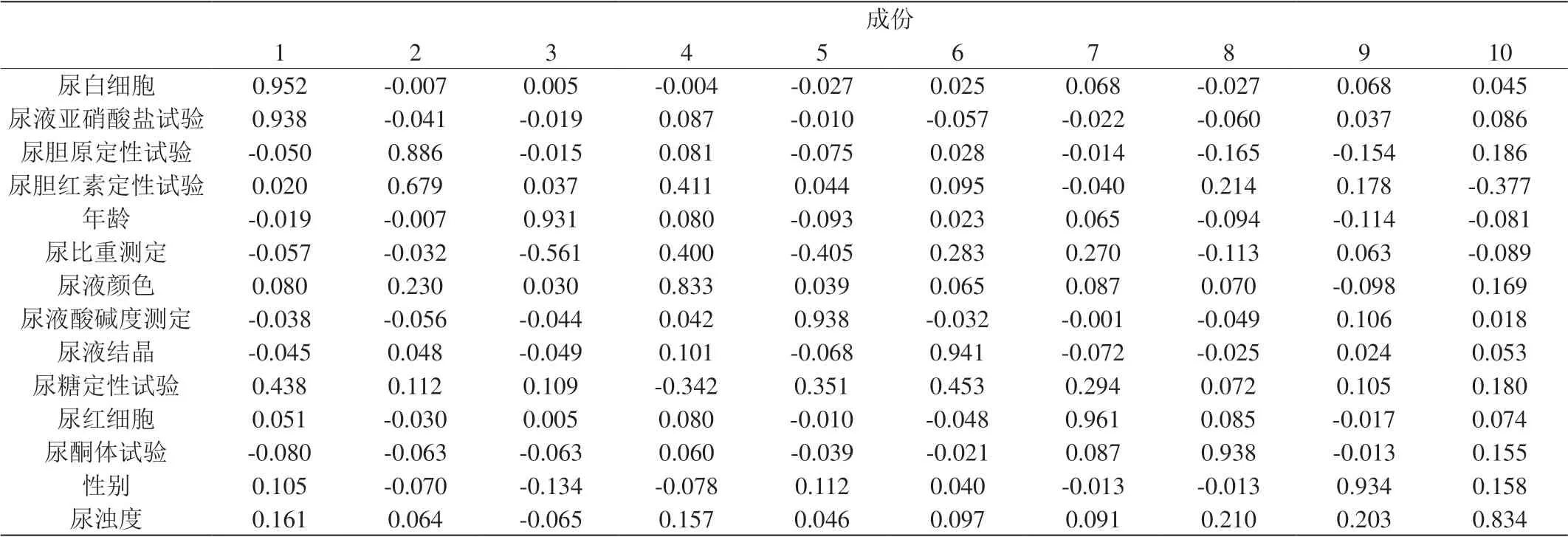
表7:尿常规主成分分析

表8:生化主成分分析
该表表示主成分分析结果,以生化表的性别项为例子,该项在第8组时概率最大(0.934),因此生化的性别项分在第8组。通过该方法,在有效的将生化和尿常规由24项和14项简化为11项和10项的同时,保持了数据绝大多数的信息(>85%)。
2.3 异常值剔除
由于糖尿病并发症某些因素偏离正常值过多,这种极少数的数值由于boosting(见下文)会具有非常大的权值,反而导致结果偏离正常范围。因此需要对异常数据进行剔除。设某组影响因素组类的数据:
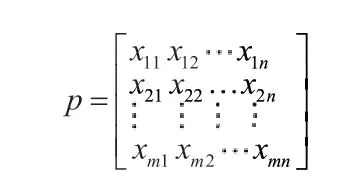
其中:n为变量个数,m为测试人员个数。
不妨设数据中正常范围极限为xj1,计算m组数据的中位数M,均值μ和均方差σ。
如果m<30,则采用改进格拉布斯(Grubbs)剔除异常值。计算个人的正常极限范围剩余误差绝对值|Vj|=|xj1-M|,选择绝对误差最大的一组数据,求出值G:
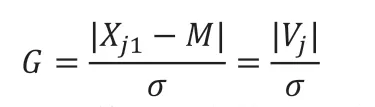
对照格拉布斯临界值表可以查询出数据个数为n时的格拉布斯临界值G(n,α),其中α为显著性水平。比较G与G(n,α),如果G>G(n,α),则对应的第j组个人数据为异常值,将其剔除。将剩余的数据重复进行上述操作,知道没有异常数据。
如果m>30,根据统计学原理会呈现正态分布,这时采用拉伊依达(Pauta)准则。若对于某一误差Vj=xj1-M,有:
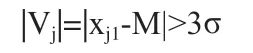
即xj1∉[μ-3σ, μ-3σ],可以认定为异常数据,将其剔除。并重复以上过程,直到没有异常数据为止。

表9:未进行主成分因素分析和异常值剔除的预测准确度
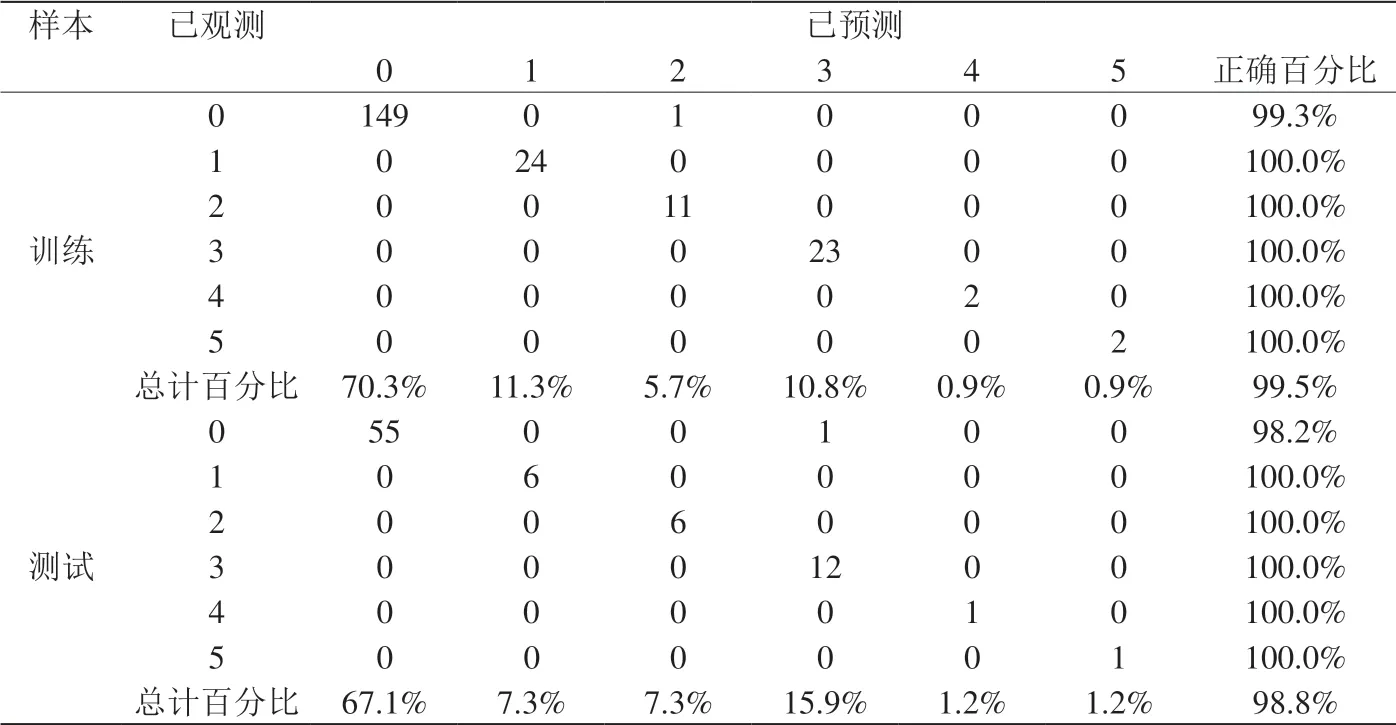
表10:进行主成分因素分析和异常值剔除的预测准确度
3 神经网络构建
神经网络构建是研究的基础,如何得到更好的模型从而使得结果真实。实验确定参数和boosting算法分别解决了样本数据量纲不同、神经网络何种结果最优以及如何提高实验精度的问题。通过这三项,建立出适合研究多种并发症的神经网络模型,量纲问题在之前数据预处理中以及解决,这里主要对后两者提出解决方案。
3.1 参数确定
一般来说,在神经网络中,神经网络层数越多,训练结构越精确,但同时训练的成本越高。由于判断层数的方法并没有很好的依据,经过实际测试,在采用4层64个神经元,激励函数relu,学习速率为0.1,初始参数为0时,结果最好。
3.2 boosting
增加预测准确性也是重中之重。并发症作为输出。其中生化指标由于样本较少、且种类丰富、因此预测准确率很低,仅仅17.23%;糖化和尿常规预测准确性分别为24.21%和44.59%。为了提高预测准确率,采用Boosting增加正确性,其核心是将当前未能成功的预测的项提高权,为下一次学习提供重点。同时该方法将样本集随机分成K部分(本文中K为10),其中N部分(本文中N为7)作为训练集,另外K全部K作为验证集合,之后依次轮回,K部分中的每一部分都有一次作为训练集,对于过学习与欠学习等问题上拥有较好的解决效果,结果准确度较高。建立过程如图3所示。
4 试验结果和分析
4.1 ROC对比
分别对不同疾病进行编号(0-正常、1-肾病、2-高血压、3-冠心病、4-糖尿病酮症和5-重症肺炎),采用4层64个神经元,激励函数relu,学习速率为0.1,初始参数为0的神经网络进行研究。其结果分别如图4、图5和表9,表10所示。
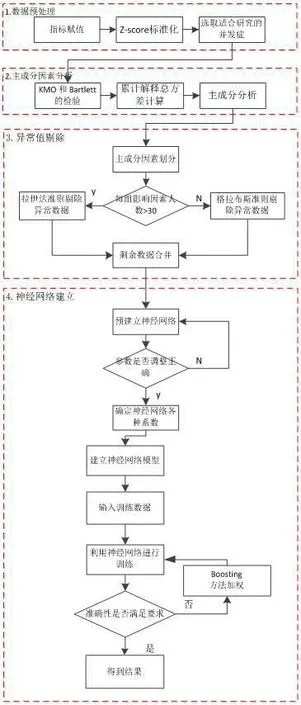
图3:神经网络建立过程
ROC曲线中,曲线面积越大,其结果准确性越大。对比图5和图4可以看出,经过主成分因素分析和异常值剔除的ROC曲线,其结果远远超出未处理的曲线。
4.2 预测准确度对比
通过预测准确度可以更精准的对比主成分因素分析和异常值剔除对于神经网络准确性的影响。
表9和表10可清晰的看出,预测准确百分比进行主成分因素分析和异常值剔除的神经网络远远优于未进行的神经网络。
4.3 主要因素定量计算
通过分别对较高的6项多种并发症进行分类,找到6项主要因素对于多种并发症的影响。之后采用常规的数学模拟方法,即通过spss软件进行拟合曲线,将这6项主要因素和他们对应权值进行了定量计算。
表11中部分结果因为样本不足导致出错,所以采用符合(*)表示,该表随着数据的增加将可以更加完善。同时本文分别对糖尿病多种并发症,通过糖化、生化以及尿常三项进行分类研究。并进一步找寻出其中较为重要的几项指标,来快速估计患者的多种并发症可能。其中经过研究,年龄是最为可能的指标。随之年龄的增加,各项多种并发症的风险会大幅度增加。通过神经网络,可以处理较为复杂的问题,并且通过主成分划分可以有效的对数据进行分组和降维,而异常剔除又可以降低特异值对结果的影响,同时Boosting方法对于提高预测准确性有着很好的帮助。通过对比,可以看出在研究并发症上神经网络有着很好的实用性。

表11:重要影响因素对主要多种并发症的定量表
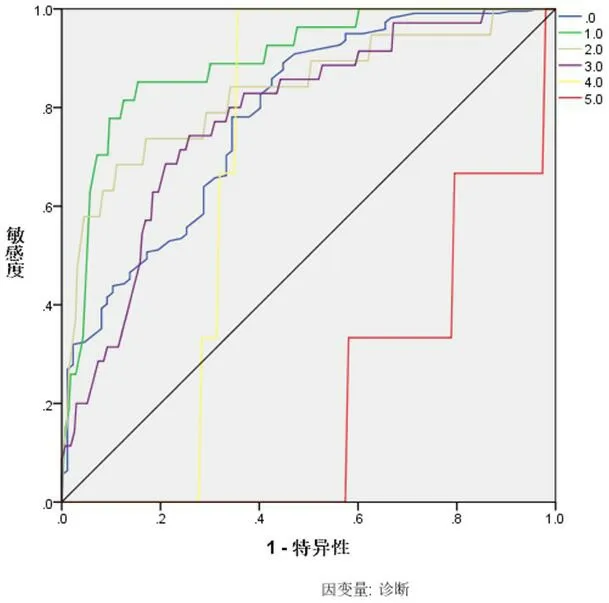
图4:未进行主成分因素分析和异常值剔除的ROC曲线
5 结论
本文主要开展了神经网络对糖尿病多种并发症的研究,从糖化、生化和尿常规三个方面对多种并发症进行了预测并进一步找寻哪些因素对结果有较大的影响。通过仿真验证了本文算法的有效性,对糖尿病多种并发症的研究有一定的参考意义。由于糖尿病患者个体差异,今后将进一步加强临床分析,提高算法的适应性。
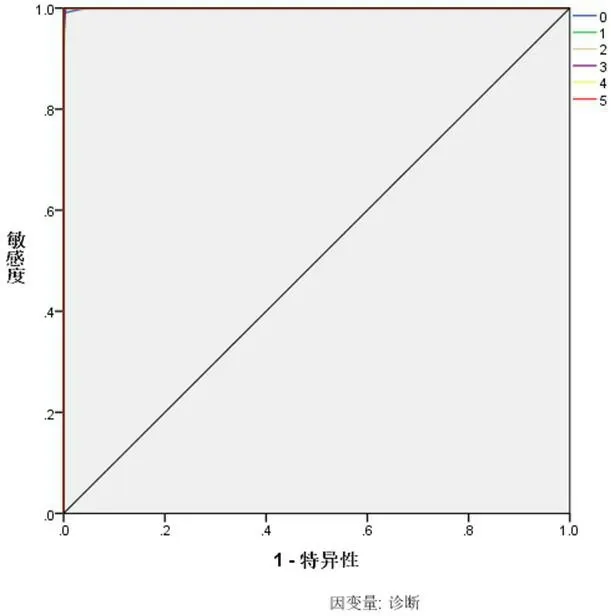
图5:进行主成分因素分析和异常值剔除的ROC曲线
