基于改进型遗传算法的内弹道优化设计

文/李鑫 张小兵 张舒玮

传统遗传算法对种群所有个体采用相同的变异率且不随种群代数变化，这样使得如果采用较小变异率，会使得算法过快收敛，容易陷入局部最优解，采用较大变异率又会导致算法收敛速度变慢，甚至不收敛。因而算法变异率的选择十分困难。目前许多学者对传统遗传算法提出了改进，其采用大多数是针对种群个体特征来确定变异率从而使遗传算法具有一定的自适应性，即当种群多样性较好时采用小变异率，而种群多样性差时采用大变异率。但是这种改进也存在明显的缺陷，因为在进化的后期，种群个体若均收敛到最优解，则种群多样性较差，但如果此时让采用较大变异率则使得收敛速度变慢，降低了算法的效率。本文尝试在传统遗传算法基础上，对变异率进行改进，增加随种群代数变化的环境变异因子，以及针对每个个体适应度特征的适应度变异因子，二者共同决定种群变异率，从而使种群个体的变异率具有自适应特性，以提高算法全局搜索能力及收敛速度。

1 改进型遗传算法

针对上述遗传算法存在的问题，我们分析变异率是提高遗传算法全局搜索能力以及提高收敛速度的关键。因此我们将改进的重点放在对种群个体变异率的控制上。

基于上述认识，我们在种群进化全过程采用递减的变异率，进化初期变异率较高，之后随代数递减，在进化后期保持较低变异率，同时在种群内部，针对每一个种群个体的适应度，在整体变异率的基础上对每一个个体的变异率进行调整，使得适应度较高的个体变异率较小，适应度低的个体变异率较大。相应的提出了随种群代数减小的环境变异因子与种群适应度变异因子，二者共同作用来确定种群个体的变异率，从而解决变异率与收敛速度之间的矛盾，提高算法的全局搜索能力和收敛速度。

1.1 变异率

1.1.1 环境变异因子

高变异率可以提高种群多样性，对于遗传算法来着则可提高全局搜索能力。环境所导致的变异率的高低对整个种群的变异率均有影响，属于该种群的基础变异率。所以我们设计了随代数变化的环境变异因子，即假设环境存在一个变化过程，即随着时间的推移能够促进变异的因素逐渐减少，在进化的初期通过带有一定随机性的高变异率来提高整个种群的多样性，从而提高算法的全局搜索能力。在进化的后期这种随机性的变异率逐渐降低以提高算法的收敛速度。具体形式如下：

1.1.2 适应度变异因子

在一个种群中，个体之间的适应度存在差异，如果对每一个个体采用相同的变异率则会导致许多问题。对于适应度较高的个体，如果采用较高变异率则可能会导致其优势消失；而对于适应度较低的个体，如果采用的变异率过低，则会导致其进化速度缓慢，算法收敛速度降低。因而应对高适应度的个体采用较低变异率，对于适应度低的个体采用较高变高变异率以提高算法的收敛速度。具体形式如下：

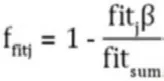
种群个体的变异率由环境变异因子和适应度变异因子共同决定，采用乘积形式将二者组合起来得到针对于每一个种群个体的变异率，具体形式如下：

1.2 改进的遗传算法流程

本文提出的改进的遗传算法继承了基本遗传算法的流程，其中种群个体的编码方式采用二进制编码，选择运算采用经典的轮盘赌选择方式，交叉操作采用单点交叉，交叉概率取Pc=0.7，变异运算采用位变异，变异率Pi,j为上述由环境变异因子和适应度变异因子共同决定的变异率。改进的遗传算法流程如下：

（1）编码：

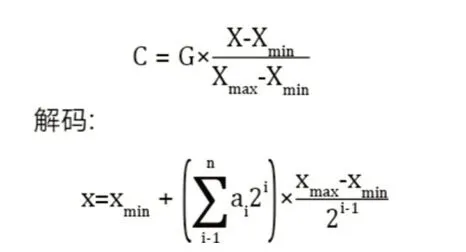
（2）生成初始种群X={x1,x2,……xn}。

（3）判断是否达到最大代数，若达到则输出当前种群，若未达到则执行步骤（4）。

（4）计算初始种群个体的适应度fitj，随机数种子使之随时间变化。

（5）生成本代环境变异因子fei。

（6）进行轮盘赌选择操作。

（7）对选择完成的个体进行交叉生成下一代的预个体。

（8）对交叉完成生成的种群个体计算适应度fitj，并且根据每个个体的适应度不同生成适应度变异因子ffitj。

（9）根据本改进型遗传算法变异概率计算的公式，计算出该代各个个体的变异率进行变异操作，采取保优策略生成子代种群，返回步骤（3）。

1.3 使用测试函数测试算法性能

本文选取了七个测试函数对改进的遗传算法性能进行了测试。

为了检验本文所提出的改进型遗传算法的全局搜索能力和收敛速度，将改进型遗传算法与传统遗传算法进行了对比，通过七个测试函数来测试二者的性能，取种群分散度和最优解为评价指标，种群分散度可以表征算法的收敛特性，最优解可以表征算法的全局搜索能力。

两种算法均采用固定代数500 代，即imax=500，两种算法均进行20 次计算，所示计算结果为20 次计算的平均值，各测试函数计算计算结果如表1所示。

通过表1数据主要对比了七个测试函数分别使用传统遗传算法与改进型遗传算法运行500 代之后得到的最优结果以及种群的分散度。通过表格数据可以看出改进后的遗传算法经过500 代计算后得到的最优解更接近标准全局最优解，且种群的分散度较小，收敛性更好。

以F1函数为例具体分析改进型遗传算法的进化过程与传统遗传算法的区别。二者进化过程中种群的分散度如图1所示。

由种群分散度曲线可以看出，传统遗传算法在进化初期即快速收敛，使得种群的分散度急剧降低，并保持较低水平，但种群最终未能收敛至全局最优点。而改进型算法在进化初期种群保持较大分散度以提高种群的全局搜索能力，在进化末期种群分散度减小，算法收敛至全局最优解。同时结合表1数据，改进型算法最终代数的分散度小于传统遗传算法，因而种群具有更好地收敛性，并且种群最终收敛至全局最优解。因而证明改进型算法的全局搜索能力与收敛速度方面都有提高。

2 结束语

本文提出了一种改进型遗传算法，通过对传统遗传算法中种群的变异率进行改进，得到了可以随种群代数变化和种群个体适应度自适应变化的变异率。利用测试函数对算法的性能进行了测试，测试结果表明改进型遗传算法在全局搜索能力和收敛速度方面均优于传统遗传算法。将改进型遗传算法应用于火炮内弹道优化设计中，也得到了更为优异的优化结果，优化的效率有所提高。通过对所得方案进行正向计算与内弹道理论曲线进行对比，验证了方案可行性，从而也验证了此改进型遗传算法在内弹道优化设计中的适用性，为今后此算法在弹道领域中的应用奠定了基础。

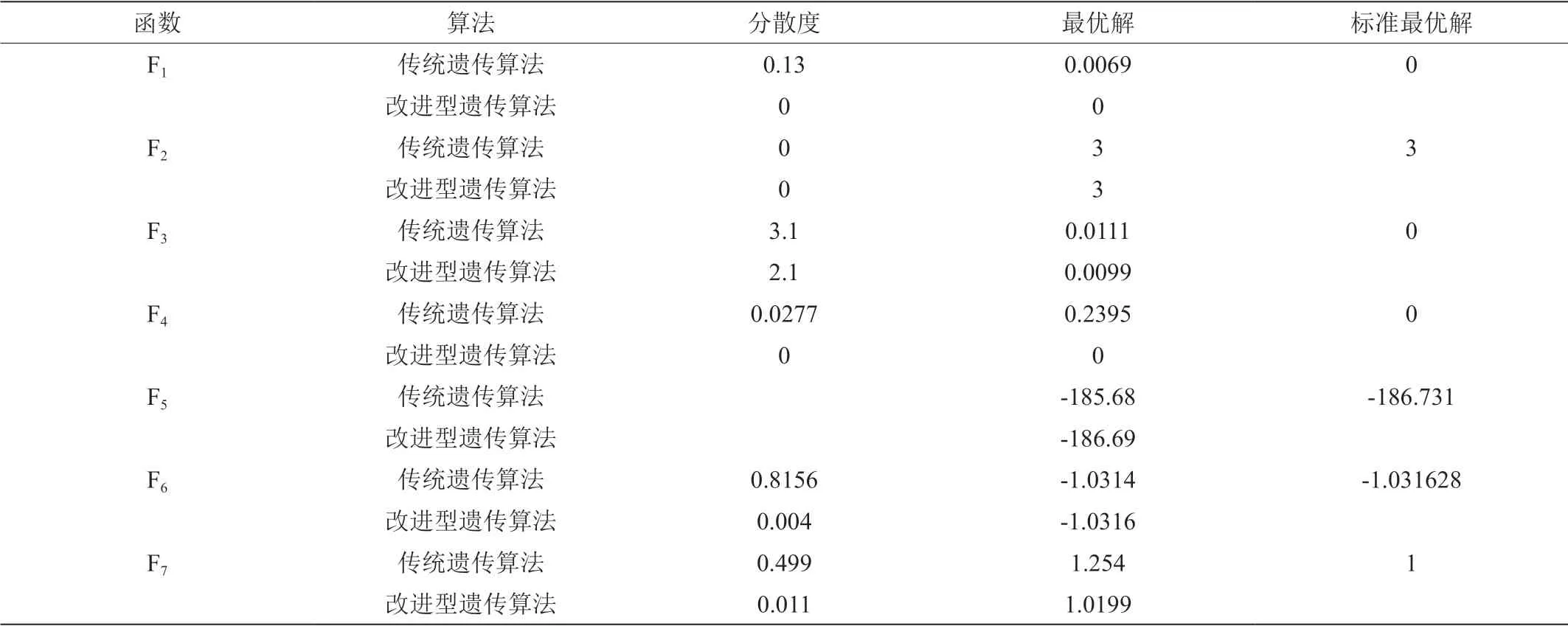
表1：测试函数结果表

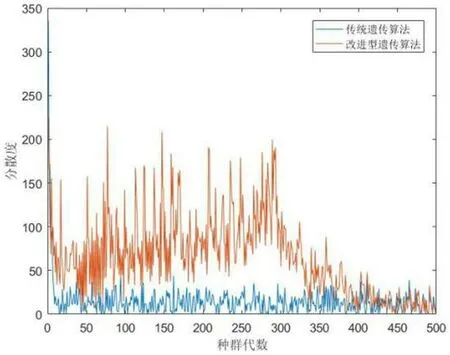
图1：种群分散度曲线