基于RBF和朴素贝叶斯的红葡萄酒质量等级分类
2019-04-26刘攀
文/刘攀
1 引言
在确定红葡萄酒的质量时,通常通过雇用一组合格的葡萄酒评委来完成。每个葡萄酒饮用者在品尝葡萄酒后对分类指数进行评分,然后对其进行求和以获得总分以确定葡萄酒的质量。因此研究一种高效可靠的智能分类识别方法很有必要;这里在红葡萄酒的多种物理化学成份测定的基础上,使用机器学习理论中的径向基神经网络和朴素贝叶斯理论相结合的构建分类模型,实现红葡萄酒质量的有效分类。
2 基于RBF和朴素贝叶斯的红酒分类模型
2.1 RBF简介
RFB(径向基)神经网络是J.Moody和C.Darken在1988年提出的基于径向基函数的神经网络算法。RBF神经网络是局部逼近网络,可以以任意精度逼近任意连续或离散函数,并且可以处理系统内难以分析的规则。特别适用于解决非线性分类和预测问题。然而,当训练样本的数量增加时,RBF网络中隐藏层神经元的数量增加,这增加了RBF网络的复杂性。结构过于庞大,从而运算量也有所增加。
RBF神经网络是具有三层结构的前馈神经网络,包括输入层,隐含层和输出层。输入层与其他神经网络相同。其结构图如图1。
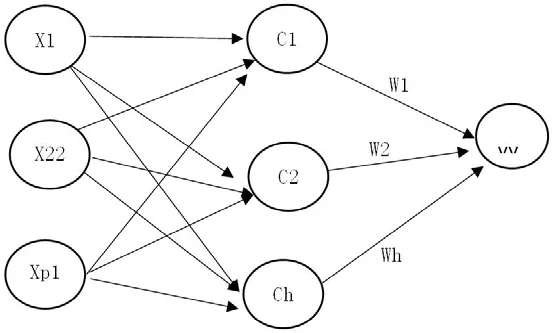
图1:RBF神经网络
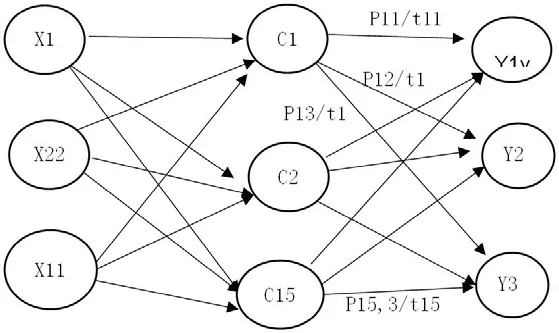
图2:RBF_NB结构图
如上图,输入层为(X1,X2,..., Xp),隐含层为(c1,c2,....,ch),输出层为 y,(w1,w2,....,wm)则为隐含层到输出层的连接权重。隐藏层的每个节点使用非线性函数h(x)作为径向基函数。隐含层的作用是将向量从低维p映射到高维h,使得低维线性不可分割的情况可以变得对高维线性可分。主要就是核函数的思想。因此,网络从输入到输出的映射是非线性的,而网络输出对于可调参数是线性的。网络的权重可以通过线性方程直接求解,这极大地加速了学习并避免了局部最小值。
径向基神经网络的激活函数可表示为高斯函数:
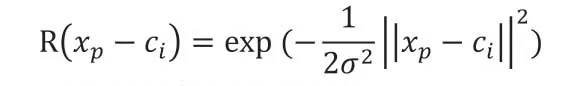
径向基神经网络的结构可以如下获得:
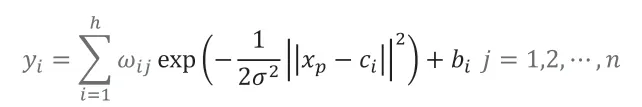
其中xp是第p个输入样本,ci是第i个中心点,h是隐层中的节点数。n是样本或分类输出的数量,bi是第i个神经元的阈值。
2.2 朴素贝叶斯分类简介
朴素贝叶斯分类器(NBC)是一种非常简单的分类算法。对于要分类的给定项目,在该事件发生的条件下,每个类别的出现概率最大,被认为属于哪个类别。朴素贝叶斯分类的思想基础如下:
(1)设x={a1, a2, a3…, am}是要分类的项目,并且每个a是x的特征属性。
(2)有类别集合C={y1, y2, …, yn}
(3)计算P(y1|x), P(y2|x), …, P(yn|x)
(4)如果P(yk|x)=max{P(y1|x), P(y2|x), …, P(yn|x) },则x∈yk
如何计算步骤3中的各种条件概率。可以这么做:
(1)查找要分类的已知分类的集合,该集合将成为训练样本集。
(2)统计数据为每个类别下的每个要素属性生成条件概率估计。即
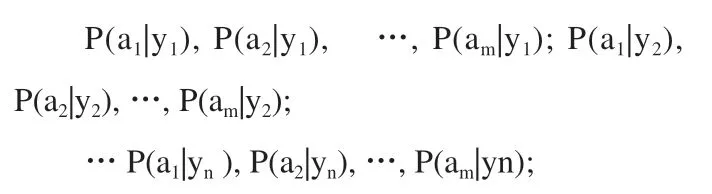
(3)如果各个特征属性是独立的,那么贝叶斯定理得出以下结论:
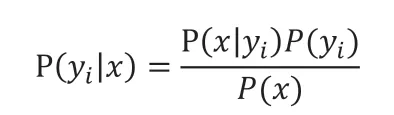
因为分母对所有类别是相同的,因此我们只需要最大化分子,并且每个要素属性是独立的,所以有
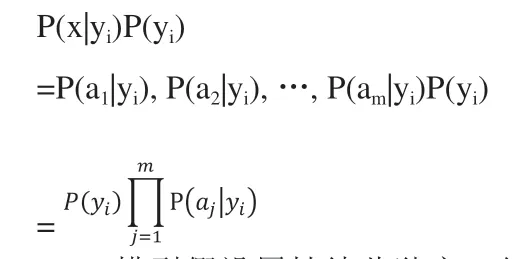
NBC模型假设属性彼此独立,但是在现实数据中,各属性会有相关性,也正是这个假设,限制了NBC模型的使用。
2.3 RBF和朴素贝叶斯相结合的模型建立
本文中使用的数据是一组红葡萄酒的物理化学参数。包括固定酸度,挥发酸度,柠檬酸,残糖,氯化物,游离二氧化硫,总二氧化硫,密度,pH值,硫酸盐,酒精,质量,共1599个样本。
品质为酒的评分,分值从1到10。把红葡萄酒等级分类,是把品质小于5的作为第一类,把品质为5和6的作为第二类,把大于6的作为第三类。
在本文中,RBF神经网络和朴素贝叶斯分类器相结合,这种分类算法称为RBF_NB,结构图如图2。
由图2可知,神经网络仍由三层结构组成,输入层神经元个数为11,即红葡萄酒的11种物理化学成分指标。 输出层神经元个数为3,输出为某一样本属于第几类的概率,从三个数据中的最大值判断样本属于第几类。 改进的RBF_NB算法主要是修改了隐含层与输出层的连接权重。其工作具体步骤为:
(1)数据的标准化旨在消除每个要素属性的维度的影响。使用matlab函数mapminmax()对数据进行归一化处理。即y = (ymax - ymin)*(x - xmin)/(xmax - xmin) + ymin; ymax=1, ymin=-1
(2)对样本进行随机排序,选择前1270行数据作为训练数据,最后329行数据作为测试数据。
(3)构建RBF神经网络。输入层神经元个数为11,即红葡萄酒数据的11维特征属性。激励函数是高斯函数,输出层中的神经元数量为3.隐含层中的神经元数量设置为h,通过实验证明,h=15具有最佳效果。使用k-means聚类,获取15个聚类中心点,方差计算公式为:
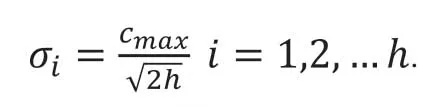
(4)利用朴素贝叶斯确定隐藏层到输出层的权值:
(5)根据RBF神经网络原理,计算出输出层的值,比较三个值得大小,确定分类。
在开始的 kmeans聚类的操作下,相似样本会聚到一类,而通过隐藏层的高斯函数,计算出的结果正是样本与中心点的距离,离中心点越近,输出值越大,反之输出值越小,而权值是该聚类的一类属于最终分类某一类的概率,该聚类里越多的样本属于最终分类的某一类, 则概率则大,反之则小。
3 实验效果比对
从收集的数据中,随机选择1270组作为训练数据,并使用329组作为测试数据。分别用NBC,RBF神经网络和RBF_NB算法进行训练,而表1反映了红酒的正确分类率。 这里为了对比的科学性,表1中的数据是进行20次训练测试后的数据。
由表1可知,RBC_NB算法不仅对训练数据有不错的分类正确率,泛化能力也不错。而RBF神经网络的泛化能力太差,出现过拟合现象。
4 结论
RBF神经网络具有收敛速度快,泛化能力强等特征,但是针对所采集的红葡萄酒物理化学成分指标的数据学习,训练数据可以达到很好的准确率,但泛化能力不理想。 本文提出的RBF神经网络和朴素贝叶斯分类相结合的模型,训练数据和测试数据都有很好的正确率,分类效果显著。这种分类模型对于酿酒厂对红酒进行分类具有一定的参考意义。
