异光谱卡氏非共轴摄远光学系统畸变的校正

刘健，白东阳，王晓曼，景文博

（1.长春理工大学 电子信息工程学院，长春 130022；2.长春理工大学 光电工程学院，长春 130022）

摄远光学系统［1］具有长焦距，小视场等特点，但是会导致体积变大。本文中的摄远光学系统基于卡塞格林系统设计的，满足以上要求，并且可见光相机和近红外相机共用一部分光学系统，具有小体积，灵活性强等优点。但是卡塞格林系统应用在摄远光学系统中会引入较大的像差，使可见光图像、近红外图像产生畸变，为了减小本摄远光学系统的测量误差，首要是去除图像畸变，从根本上去除摄远光学系统的像差。

随着摄像机畸变校正技术的发展，在生产中张正友相机标定法［2］被广泛应用于单个大视场短焦距摄像机畸变校正。在单视点折反射相机标定领域，传统方法有：理想情况下的直接线性变换（DLT）法；考虑了径向崎变的Tsai两步标定法［3］；考虑了切向畸变的 Weng 等人的迭代法；Martins［4］提出的双平面模型法等；中国科学院的孟晓桥、胡占义［5-6］教授在相机自标定方法中提出更具稳定性的基于曲线拟合的圆形标定法；吴毅红教授提出的应用更广泛的平行圆平面标定法等都对摄像机的标定技术做出了巨大贡献。

摄远光学系统存在的系统畸变，关键在于不共轴的两个相机，光谱范围不同，实现摄远光学系统的校正是依据空间环境中物体的几何信息与图像信息之间的关系得到的成像模型，并且通过成像模型得到理想无畸变图像，摄远光学系统校正要涉及畸变校正模型的构建和摄像机校正方法的选择。畸变校正模型一般可以分为两大类：线性模型和非线性模型，线性模型不考虑光学系统畸变，简单快速，但精度低；非线性模型引入畸变参数从而使校正精度提高，但是对于本摄远光学系统适用性较低，计算繁琐，速度慢。考虑到在应用领域中基于卡塞格林系统设计的不共轴的两种波长范围摄远光学系统的高精度的测量要求，本文提出了一种异光谱卡氏非共轴摄远光学系统的校正方法。全面地考虑了摄远光学系统的各个参数。

1 双色卡氏非共轴摄远光学系统校正

1.1 构建校正模型

在构建摄远光学系统校正模型前，这里对该系统结构做简单说明。光学系统结构简图如图1，由卡塞格林［7］反射结构、光学透镜、直角分光棱镜、滤光片及图像传感器组成。卡塞格林反射结构满足了光学结构长焦距体积小的需求，直角分光棱镜将入射光分成两束，分别至可见光相机、近红外相机成像，如图1所示。鉴于光学系统［8］的设计，从机械装调或者成像器件的物理特性方面很难减小光学畸变，本文所述的光学系统，能够缩短成像时间，降低背景噪声，提高光斑图像信噪比，从而降低光学系统的测量误差，提高光学系统的测量精度，但同时引入卡塞格林系统的像差。因此，本文通过构建摄远光学系统校正模型，实现对本摄远光学系统的校正。本文摄远光学系统校正模型选用的是扩展的针孔模型，即在小孔成像的过程中考虑畸变因素，模型建立的是完成世界坐标系到图像二维点的映射关系［9］，所以，为了定量描述光学成像过程，分别建立世界坐标系，入射光坐标系(O-XCYCZC)，可见光相机坐标系(O-XC1YC1ZC1)，近红外相机坐标系(O-XC2YC2ZC2)，可见光图像物理坐标系1)，近红外图像物理坐标系(o2-x2y2)，可见光图像像素坐标系(o1-u1v1)，近红外图像像素坐标系(o2-u2v2)，如图2所示。

图1 异光谱卡氏非共轴摄远光学系统简图

图2 坐标系关系图

世界坐标系(O-XWYWZW)；以入射光的光轴为Z轴，垂直于光轴的平面为XOY面，建立入射光坐标系(O-XCYCZC)，入射光坐标系旨在说明两相机存在共轴部分；世界坐标系与入射光坐标系之间关系如下：

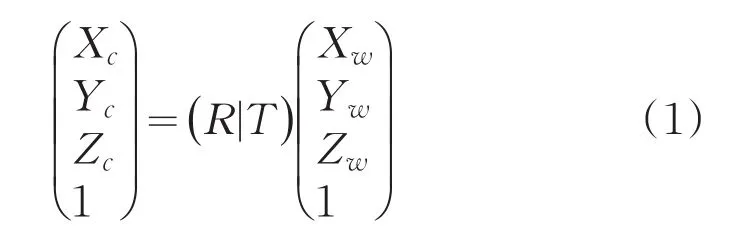
式中，(R|T)为刚体变换矩阵，实现世界坐标系到入射光坐标系转换。

以可见光相机的光轴为Z轴，垂直于可见光入射光轴为XOY面，建立可见光相机坐标系(O-XC1YC1ZC1)；进而得到世界坐标系与可见光相机坐标系之间的关系：

式中，(R1|T1)为刚体变换矩阵，实现世界坐标系到可见光相机坐标系转换。

以近红外相机的光轴为Z轴，垂直于近红外入射光轴为XOY面，建立近红外相机坐标系(O-XC2YC2ZC2)；进而得到世界坐标系与近红外相机坐标系之间的关系：

式中，(R2|T2)为刚体变换矩阵，实现世界坐标系到近红外相机坐标系转换。

以图像中心点为原点，横轴为x轴，纵轴为y轴建立图像物理坐标系；以二维图像左上角为坐标原点，横轴为u轴，纵轴为v轴，建立图像像素坐标系。

得到可见光图像像素坐标系与世界坐标系之间关系用齐次方程表示为：

式中，fx1，fy1，u10，v10为相机内参数［10］，M11为可见光相机内参矩阵，M12为可见光相机外参数矩阵；经过类似的坐标系变换可得近红外图像像素坐标系与世界坐标系之间的关系：

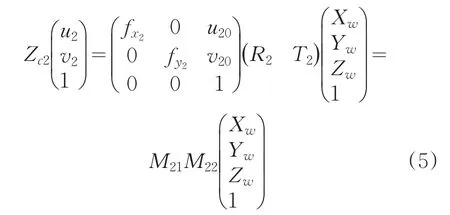
式中，M21为近红外相机内参矩阵，M22为近红外相机外参数矩阵。

世界坐标系与可见光相机坐标系和近红外相机坐标系之间关系用外参数矩阵表示。两相机坐标系与图像坐标系用内参数联系。本文所涉及的光学系统，如图2所示，共轴部分就是入射光坐标系的ZC轴，计算过程将其合并到两相机坐标系，为一种等效方法。

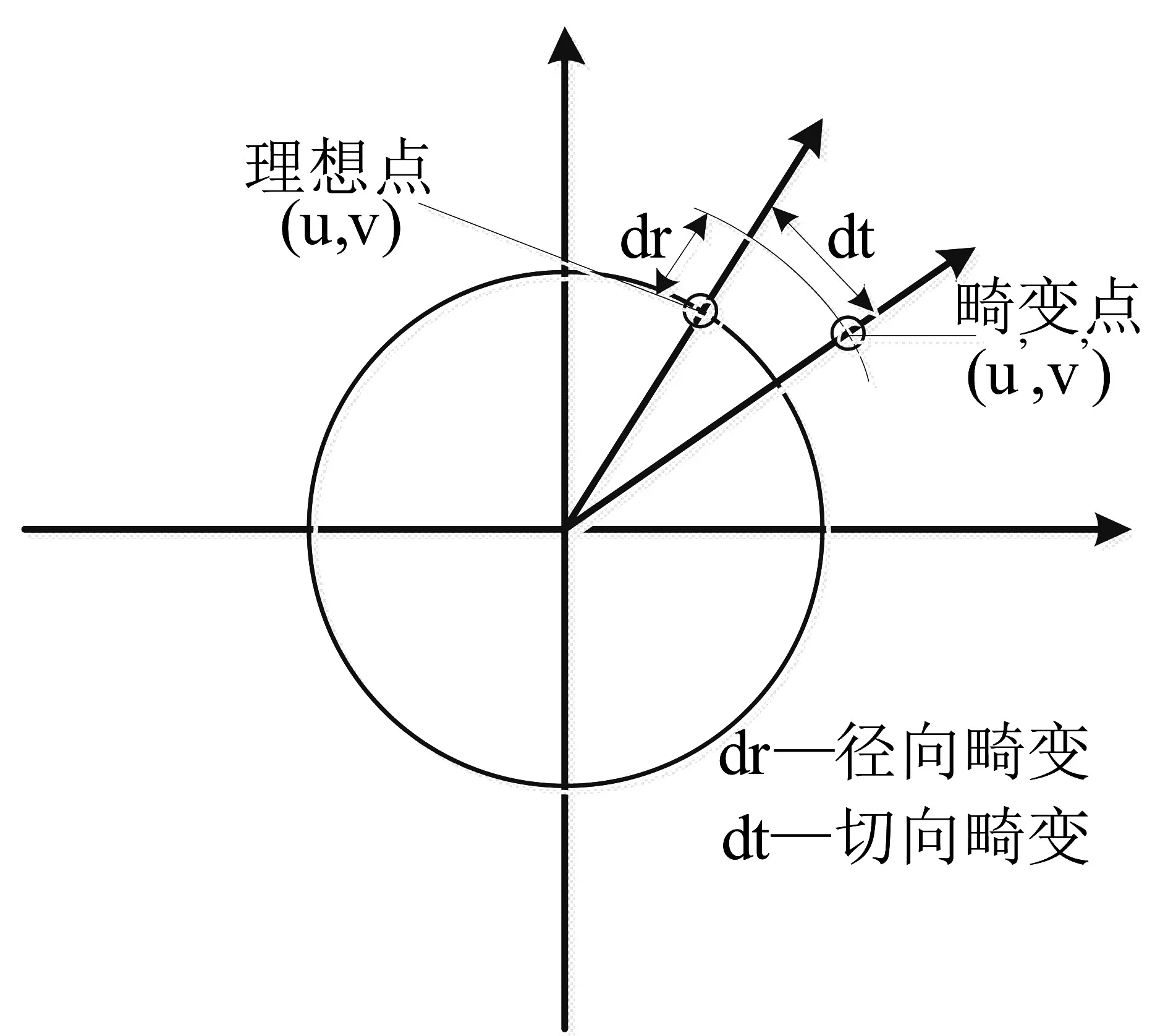
图3 径向畸变和切向畸变

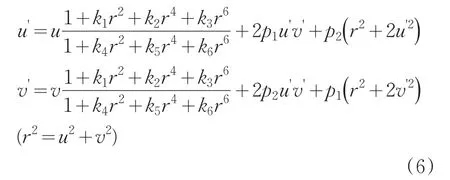
摄像机镜头存在一些畸变，主要是径向畸变、切向畸变等，如图3。由于径向畸变和切向畸变，理想点和畸变点之间的关系通过畸变系数表示，公式（6）中k1，k2，k3，k4，k5，k6为径向畸变，p1，p2为切向畸变。式中，定义畸变向量Tdc=[k1,k2,k3,k4,k5,k6,p1,p2]，公式（6）通过畸变系数说明畸变点与理想点之间的关系，用畸变向量Tdc表示，所求的畸变向量的维数影响所需图像的个数。通过解算出相机的内参矩阵、外参矩阵及畸变向量，完成本文摄远光学系统的校正。

1.2 畸变校正

在获取摄远光学系统校正模型后，搭建校正系统，图4为搭建校正系统结构图，如图4所示，结构包括：光源；在光源的一侧依次设有平行光管以及摄远光学系统；摄远光学系统与计算机相连接；平行光管内设有网格板。获取图像之前，首先调整各个设备的位置，使得网格板中心点成像于可见光图像的中心，如图5所示。

图4 校正系统结构图

图5 网格板

本光学畸变校正方法流程图如图6所示。

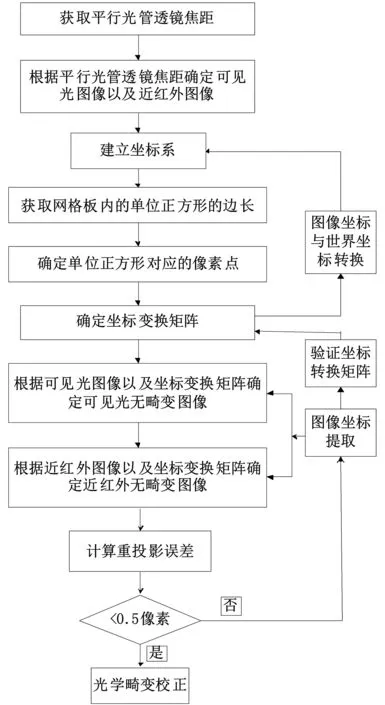
图6 光学畸变校正方法流程图

所用平行光管为可调视度式平行光管［11］，产生平行光时焦距为f'，平行光管微调标尺刻度为r。获取平行光管产生可见平行光时的平行光管透镜焦距，与折射率关系公式为：式中，k为比例常系数，n为空气中折射率，n'为可见光相机透镜折射率。

根据平行光管透镜焦距确定可见光图像以及近红外图像，由以上可得：

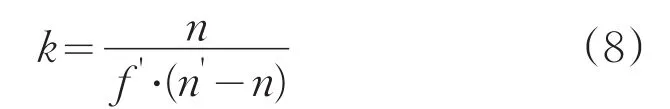
由成像公式计算可得可见光时，网格板距离平行光管透镜的距离；近红外光时，网格板距离平行光管透镜的距离。

因此，相对于平行光管焦距调整相对位置为：

可见光时：ΔuVis=uVis-f'；

近红外光时：ΔuIR=uIR-f'。

对应平行光管微调标尺刻度为：

可见光时：rVis=r+ΔuVis；

近红外光时：rIR=r+ΔuIR。

调整网格板的位置，分别采集可见光与近红外图像。循环调节网格板位置，调整摄远光学系统，使可见光相机和近红外相机获得不同拍摄角度的图像，并重新采集多对不同角度的可见光图像以及近红外图像，且循环次数N大于等于14次。

建立坐标系如图2所示，世界坐标系(O-XWYWZW)与可见光相机坐标系(O-XC1YC1ZC1)和近红外相机坐标系(O-XC2YC2ZC2)需要求解12个参数，其中，三维坐标系变换为旋转和平移关系，旋转和平移分别3个参数，共6个参数，这里将共轴部分合并到两相机坐标系。可见光相机坐标系(O-XC1YC1ZC1)与可见光图像像素坐标系(o1-u1v1)之间关系即为相机内参数为4个参数，同理近红外相机也存在4个内参数。共需要求解20个参数。

对于平面图像能够提供8个方差，即映射一个正方形到四边形可以用4个(x,y)来描述，对于四个视场就有8*4=32=4*6+4+4，即求解所有的参数，至少需要四个视场，即可见光相机与近红外相机共需要四个视场，因此共需要4幅图像（可见光两幅，近红外两幅）。为了提高精度，减小随机误差，多次试验，图像个数N大于等于14，重投影误差小于0.5像素，表1为重投影误差统计表，如表1所示，

表1 重投影误差与图像个数统计表

由表1可知，获取图像个数越大，重投影误差越小，标定效果越好。

网格板包括多个单位正方形，获取网格板内的单位正方形的边长，根据小孔成像模型确定单位正方形对应的像素点。根据像素点以及图像坐标系确定坐标变换矩阵，坐标变换矩阵用于将畸变图像变换到无畸变图像。畸变图像为可见光图像以及近红外图像，无畸变图像包括可见光无畸变图像以及近红外无畸变图像。计算重投影误差，重投影误差小于0.5像素，满足要求。如果不满足要求，则重新进行图像坐标提取，并且考察坐标变换矩阵参数的正确性。

2 校正实验及结果

经过以上摄远光学系统校正方法，采集图像如图7（a），图8（a）所示，选择以图像中心9*9矩阵大小的网格角点，即如图5中虚线框内9*9的网格点所成的像，提取网格角点坐标。提取坐标如图7（b），图8（b）中标记的网格点坐标，其中，图7（b）是可见光图像标记的网格点，图8（b）是近红外图像标记的网格点；其中，所标记的网格点坐标是亮色的圆点。

摄远光学系统校正模型前面已经得出。由世界坐标系到图像像素坐标系用矩阵Tm表示，可见光与近红外分别用Tm1，Tm2表示。如图5中网格板，每一个小格都是边长为d的正方形，通过成像模型可以计算出边长d在理想图像上对应的像素大小，得出畸变向量Tdc，结合矩阵Tm得到理想无畸变图像坐标Cd，因此，之前所提取的畸变坐标记为C，Cd与C之间关系为：

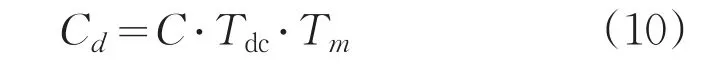
式中，Tdc⋅Tm表示畸变图像到无畸变图像的坐标变换矩阵。由重投影误差统计数据可知，图像个数大于14时，满足一般要求，一次试验采集20帧图像，得出可见光相机内参数矩阵M11、旋转矩阵R1、平移矩阵T1、畸变向量Tdc1和近红外相机内参数矩阵M21、旋转矩阵R2、平移矩阵T2、畸变向量Tdc2，这里畸变向量保留5维：

设光学校正后图像为I'，带有光学畸变的图像为I，根据矩阵Tm得到三者关系：

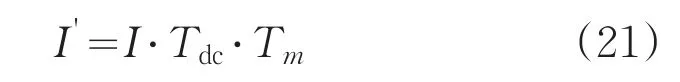
同步采集图像，经过矩阵变换，得到可见光与近红外无畸变图像，可见光图像如图7（a）、近红外图像如图8（a）所示图像，进行矩阵变换得到可见光无畸变图像如图7（c）、近红外无畸变图像如图8（c）所示的图像。

图7 可见光图像

提取可见光图像如图7（b）中心9*9网格区域坐标和近红外图像如图8（b）中心9*9网格区域坐标，利用坐标变换矩阵计算重投影误差，统计五组试验数据如表2。

经过试验得出的摄远光学系统中可见光与近红外相机的光学畸变校正矩阵应用于光学系统校正，得出表2的重投影误差精度达到0.4像素，可见光重投影误差的RMS值为0.070433，近红外重投影误差的RMS值为0.048049，该试验结果可以很好地应用于异光谱卡氏非共轴摄远光学系统畸变的校正。

图8 近红外图像

表2 五次实验重投影误差统计

3 结论

本文提出了一种对异光谱卡氏非共轴摄远光学系统的光学畸变校正方法，解决了基于卡塞格林系统的摄远光学系统存在像差的问题。在求解的过程中，用平行光管提供等效目标光源，实现摄远光学系统高精度标定，简化可见光相机与近红外相机需要求解的多个参数，满足了快速计算的工程原则，该方法的光学畸变校正结果重投影误差小于0.4像素，实验结果表明：该方法在基于卡塞格林系统设计的不同光谱、不同分辨率及非共轴的摄远光学系统中，一次标定达到在测试过程中自动调优的效果，在外场试验各项精度测试过程中发挥了重要的作用。