一种基于偏微分方程的信号增强模型
2019-04-25李远禄
李 俊 李远禄,2 蒋 民
(1.南京信息工程大学自动化学院,南京,210044;2.江苏省大气环境与装备技术协同创新中心,南京,210044)
引 言
峰检测被应用于很多领域,如心电图、基于质谱分析的癌症诊断、水质分析以及化学混合物鉴定等[1-2]。由于实验环境和仪器分辨水平等因素的影响,以及谱峰自身的特点,会存在部分弱峰,或者部分重叠峰,若直接对信号进行峰检测,容易造成峰的漏检和错检。因此,如何提高重叠峰的分辨力,或者对弱峰进行增强是一个关键问题[3]。
常见的信号增强方法包括Fourier去卷积方法、连续小波方法和导数谱方法。Kauppinen等人提出了Fourier去卷积法[4];Du等人提出了连续小波的峰检测方法[5];导数谱方法是增强信号的常用方法[6],目前被广泛应用于水体分析、乳腺肿瘤检测和心电图检测等[7-9]。然而导数谱方法在增强谱峰的同时也会降低信号的信噪比,因此通常将导数谱方法和平滑方法相结合使用,如与小波方法结合用于化学信号检测[10],与Savitzky-Golay方法结合测定红外光谱[11],与高斯平滑方法结合用于蛋白质谱峰检测[12]等。
平滑方法较多,主要包括时域和频域两类方法。在时域中,最简单的平滑方法是滑动均值滤波,即将相邻的奇数个点求平均值代替原中心点[13];Savitzky-Golay滤波目前被广泛使用,该方法是一种广义的滑动均值滤波方法,它将一小组连续数据点做最小二乘拟合,并将多项式拟合曲线的中心点作为输出[14],相比于滑动均值滤波法,该方法具有更好的保峰效果;高斯滤波是对滑动均值滤波平滑窗口的改进方法,使用高斯函数作为平滑窗口[15];类似地,还有使用kaiser窗作为平滑窗口的滤波方法[16]。在频域中,需要先将信号转换到频域,再将高频系数抛弃,然后重构得到平滑信号。小波方法是目前最常用的频域平滑方法,该方法可以较好地保护信号的特征,然而结果与所用小波基和尺度有关,不同尺度下所得结果可能相差很大[17-18]。
20世纪80年代,Witkin发现齐次线性扩散方程的解等价于一定尺度下初始信号与高斯函数的卷积,因此偏微分方程在信号处理中越来越受到重视[19]。然而线性扩散滤波在处理信号时没有考虑信号的特征,在去除噪声同时也可能会模糊信号的细节。针对这个问题,Perona和Malik在1990年提出了经典非线性扩散方法,它根据原始信号的特征在信号的不同位置设置不同的扩散强度,既有好的平滑效果,又能保护信号细节特征[20]。近年来,经典非线性扩散滤波被广泛运用到图像处理中,在保护图像纹理特征方面有很好的作用[21-23]。
鉴于非线性扩散模型有保护信号细节特征的能力,本文将非线性扩散与导数谱方法结合,得到一种新的信号增强模型。具体步骤是先对原信号应用导数谱方法增强,再将增强后的信号作为非线性扩散模型的初始信号,经扩散后得到平滑的增强信号。
1 基于非线性扩散的导数谱增强模型
经典非线性扩散模型如下[20]

式中:f(x)为原始信号;g[u(x,t)]为扩散函数。
导数谱增强模型如下[6]

式中:f为原始信号;F为增强后的信号;n为导数阶次,通常取偶数;c为增强系数。
将经典非线性扩散模型与导数谱增强模型相结合,得到本文模型为

式中

目前,已有多种非线性扩散方程的求解方法[21-22],由于有限差分易于处理,并且实际数字信号已经离散,因此本文采用有限差分格式求解。
有限差分格式主要有两种方案,分别是显式差分格式和隐式差分格式,由于隐式差分格式是无条件稳定的,因此本文选取隐式差分格式对模型进行离散。
隐式差分格式为

式中:i表示序号;k表示第k次迭代;τ为时间离散步长;h为空间离散步长。

将式(6)写成矩阵与向量的形式,有

式中

并且Bk-1是可逆的。
具体算法为:
(1)给定增强系数c,扩散强度控制参数λ,迭代次数N,时间步长τ,其中h可以取1;
(2)按式(2)得到原始信号的增强信号U0;
(3)按式(4)得到离散的gk-1i并计算βk-1i;
(4)构造矩阵Bk-1;
(5)按式(7)迭代,即可得到平滑的增强信号。
2 模拟数据及结果讨论
2.1 模拟数据
本文用洛伦兹峰来验证所提出的模型,它的产生方法如下

式中:n为峰的数目;Ai,μi和σi分别为第i个峰的峰高、峰位置和峰宽参数。
2.2 扩散函数对扩散过程的影响
非线性扩散模型与线性扩散模型的区别在于存在控制扩散强度的扩散函数,如果扩散函数为常数,则退化成线性扩散模型,也就是常见的高斯平滑。它的缺点是在去除噪声的同时会钝化峰,尤其在信噪比较低时,容易形成重叠峰。非线性扩散模型使用高斯函数作为扩散函数,扩散强度随峰高的增加而减弱,从而到达保峰的目的。
在扩散函数中,λ是控制扩散强度的阈值。如果λ取值很大,扩散函数的值趋近于1,这时相当于高斯平滑。当选择合适的λ时,既可以保峰又可降噪。通常λ的值可根据经验给定,当然也可根据公式给定,若期待最高峰处的扩散强度为一个小值ε,那么第k次迭代的λ可设为

当噪声水平较高时,需要在前几次迭代中取较大的ε值,通常情况下取0.9以上;之后的迭代中则可取较小的ε值,从而较好地保护峰的形状。
图1是通过式(8)得到的由两个不同高度的洛伦兹峰组成的模拟信号。对图1中的噪声信号做平滑,设较低峰处的扩散强度为0.1,则较高峰处的扩散强度ε为0,其扩散函数如图2(a)所示,平滑结果如图2(b)所示,平滑后较高峰处仍存在较大噪声;设较高峰处的扩散强度ε为0.1,其扩散函数如图2(c)所示,平滑结果如图2(d)所示,平滑后效果较好。由图2可以看出,对最高峰取不同的扩散强度ε,平滑效果是有差异的。

图1 模拟信号Fig.1 Simulated signal

图2 不同情况下扩散函数对平滑结果的影响Fig.2 Influence of diffusion function on smoothing results under different conditions
2.3 信号产生与实验对比
为了对比增强与未增强的效果,本文通过式(8)的洛伦兹峰模型产生模拟信号,如图3所示。图3(a,b)分别是由8个和12个洛伦兹峰组成的信号,信号中存在弱峰和重叠峰,可以看出噪声信号增强后噪声水平也会被增强。
图4是将图3中2个信号经过本文模型增强后得到的结果。为对比导数谱对峰的增强效果,需要为增强系数取一个合适值,本文对增强系数分别取0(未增强)和其他值时的增强效果进行对比。实验中两个信号取相同的平滑参数,时间步长τ取1,迭代次数取20,前5次最高峰扩散强度ε取0.99,之后取0.05。由图4可以看出本文模型具有很好的峰增强效果,能增强弱峰的幅度和提高重叠峰的分离度。
为更好地表现增强的效果,本文将图4的检测结果用表1表示。通过图4和表1的对比可以看出,只对噪声信号做平滑,其中的弱峰会和噪声容易一起被平滑掉,还容易导致重叠峰,从而影响检测结果;使用本文模型处理后,信号中的弱峰幅度被增大,如信号1中x=150处,x=310处,信号2中x=270处,x=420处的峰,同时重叠峰的分辨会提高,如信号1中x=270处,信号2中x=160处,x=330处,x=380处的峰。

图3 重叠峰真实信号、噪声信号和增强后的噪声信号(SNR=20 dB)Fig.3 Real signal,noisy signal and enhanced noisy signal of overlapping peaks(SNR=20 dB)
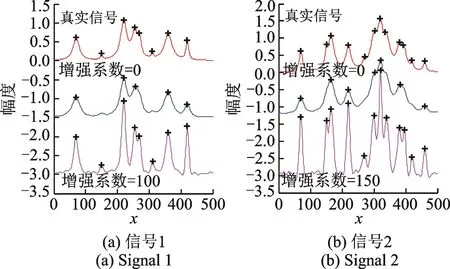
图4 基于非线性扩散的导数谱增强模型效果对比Fig.4 Comparison for the derivative spectrum enhancement models based on nonlinear diffusion
2.4 基于非线性扩散的导数谱增强模型与其他模型的对比
导数谱方法常和小波方法(WMD)或Savitzky-Golay方法(SGD)结合应用于信号增强,因此为进一步验证基于非线性扩散的导数谱增强模型(CDD)的效果,将其与前两种模型作对比。在选取参数时尽量保证所有子峰都被检测到,同时观察信号中其他位置的平滑效果,两个信号增强系数分别取100和150,WMD尺度取3,小波基选择“sym12”,SGD框长度取13,阶次取2,迭代次数取10,3种模型对图2两个信号的增强结果如图5所示。
通过两组结果的对比,可以发现3种模型都具有较好的峰增强效果。然而和真实信号相比,WMD模型和SGD模型的增强结果中新增加了一些伪峰(与真实峰相比新产生的峰),由于这些伪峰的幅度较大,容易导致误检,如信号1中x=200处,信号2中x=200处和x=250处等。相比于其他两种模型,本文模型在增强峰的同时,对峰以外的部分具有更好的去噪效果,有效降低了峰检测中伪峰的数目。
2.5 基于非线性扩散的导数谱增强模型的应用
基于非线性扩散的导数谱增强模型可以应用于MALDI质谱,MALDI质谱的检测对于发现疾病生物标志物和研究药物代谢等方面具有重要意义。本文从Bioinformatics Toolbox中选取一组MALDI模拟数据作为实验样本(http://bioinformatics.mdanderson.org/Supplements/Datasets/Simulations/index.html),使用本文模型对其做处理。为方便对比,分别取增强系数=0(未增强)和增强系数=200,处理结果如图6所示,其中竖线表示真实峰的位置。
从图6可以看出本文模型对质谱具有一定的增强效果,弱峰的高度被增加,同时从8 200左右的位置可以看出该模型能有效增加重叠峰的分离度。

表1 使用基于非线性扩散的导数谱增强模型后峰检测结果对比Tab.1 Comparison of peak detection performance using derivative spectrum enhancement model based on nonlinear diffusion
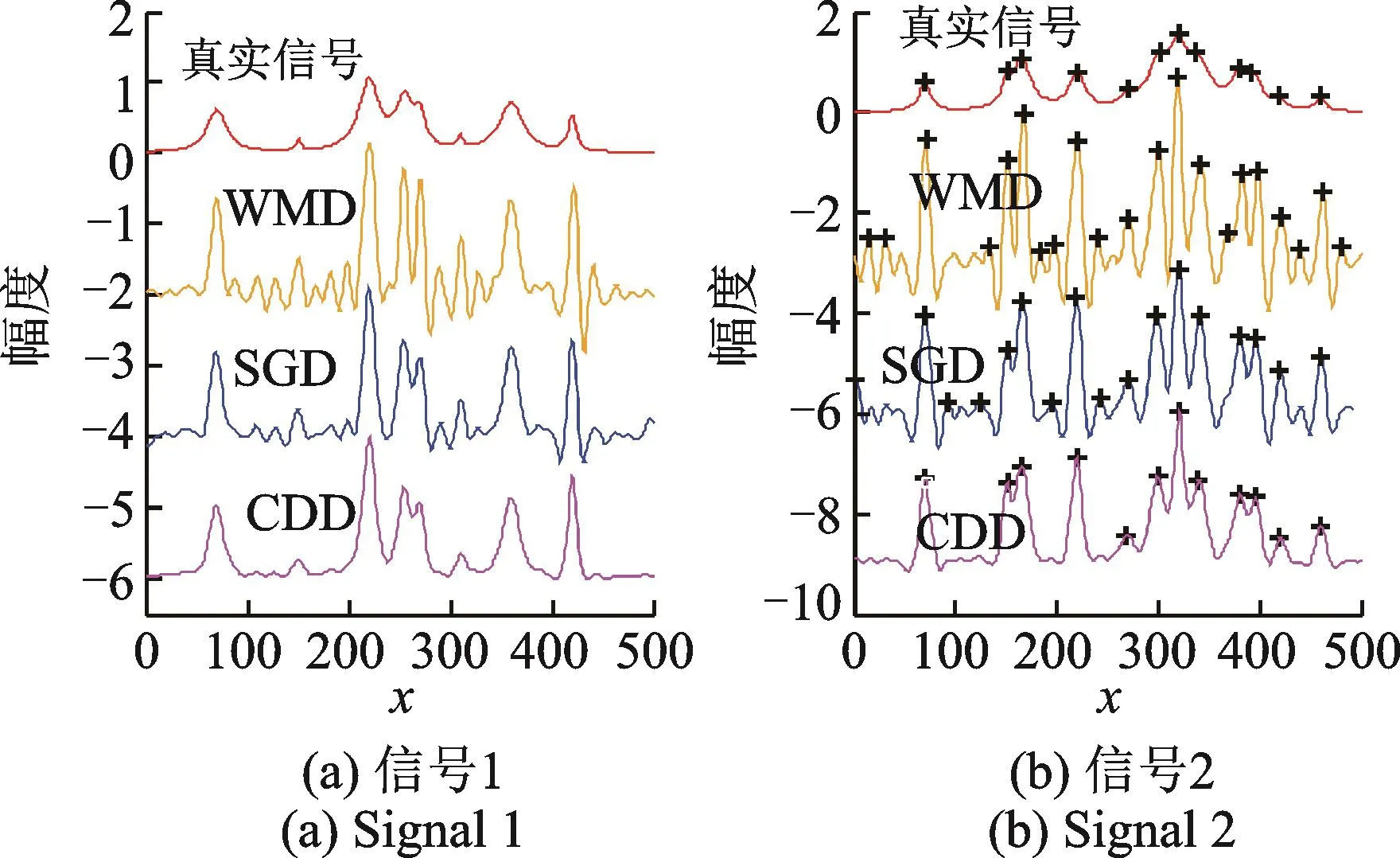
图5 不同模型信号增强结果对比Fig.5 Comparison of enhancement results for different models

图6 应用增强与未增强质谱的处理效果对比Fig.6 Comparison for the mass spectrometry with enhanced methods
3 结束语
本文提出了一种新的信号增强模型——基于非线性扩散的导数谱增强模型,并通过模拟信号和MALDI质谱验证所提模型的效果。结果表明所提模型能有效增强峰的特征,当信号中存在噪声,并有弱峰和重叠峰存在时,该模型能在去除噪声的同时有效增强弱峰的幅度和提高重叠峰的分离度。
