基于不完全信道状态信息的多用户MIMO中继系统预编码算法

陈小敏 方 竹 胡续俊 朱秋明 陈 兵

（1.南京航空航天大学电子信息工程学院，南京，211106；2.南京航空航天大学江苏省物联网与控制技术重点实验室，南京，211106）

引 言

多输入多输出(Multiple-input multiple-output,MIMO)技术可以在不增加带宽的前提下成倍地提升系统的容量和频谱利用率[1]。将中继运用到MIMO系统中并结合预编码技术，能够在提高系统吞吐量同时增加无线网络的覆盖范围。将现有的MIMO和中继等无线通信技术进行融合，进一步挖掘其潜在优势是当前5G技术的热点内容。目前为止，针对单用户MIMO中继系统，国内外学者分别以最大化信道容量、服务质量和最小均方误差为准则对其预编码方案进行了详尽的研究。而多用户MIMO中继系统更契合实际场景应用，成为当前的研究热点。

基于多用户MIMO中继系统预编码算法的研究可见文献[2-8]。文献[2]提出了以最小化发射功率，信干噪比(Signal to interference and noise ratio，SINR)为约束的预编码设计方案。文献[3]以最大化信道容量为准则，发射功率为约束联合设计预编码。文献[4]则将单用户双跳MIMO中继系统扩展至多用户多跳MIMO中继系统。文献[5]分析了基于最小均方误差（Minimum mean-squared error，MMSE）和服务质量(Quality of service，QoS)准则的多用户MIMO中继系统的预编码设计方案。文献[6]则采用脏纸编码对多用户中继网络进行了研究，该方案采用矩阵变换性质将原始预编码设计问题转化为可用迭代注水算法解决的标量变量问题，继而可求得预编码矩阵。然而，文献[2-6]均假设信道状态信息（Channel state information,CSI）完全已知。文献[7]基于MMSE准则在仅考虑信道估计误差的情况下提出了联合迭代算法。文献[8-9]基于高斯马尔科夫信道状态信息误差模型和最大化信漏噪比(Maximum signal to leakage and noise ratio，Max-SLNR)准则，提出了一个自适应的基站预编码算法。文献[10]则在考虑信道估计误差和天线相关性的情况下对上行多用户MIMO中继系统进行了预编码算法设计，但没有考虑信道反馈延迟。而对于实际MIMO中继系统，由于信道估计方法的局限性以及反馈链路的时延性，信道反馈延迟很难避免。

本文综合考虑信道中存在反馈延迟和估计误差的情况，以改善系统的误比特率性能为优化目标，对上行多用户MIMO中继系统的预编码算法进行研究，以MMSE为优化准则，将求解发射端、中继节点、接收端矩阵的复杂非凸问题分解为3个独立的子优化问题。发射端天线服从空间独立分布，可以先确定发射端预编码矩阵。中继矩阵求解的凸优化问题可转化为SDP问题，继而采用CVX工具箱求解。接收端处理矩阵可利用线性搜索法求解。最后采用联合迭代法联合优化各节点的预编码矩阵。仿真结果验证了所提算法的有效性。

1 系统模型

考虑图1中发射端存在K=ns个用户的上行多用户MIMO中继系统。发射端在中继的协助下向接收端发送信息，中继节点和接收端分别具有nr和nd根天线，每个用户配备单天线。

在第一个时隙内，K个用户同时发射信号至中继节点，其中xk(k=1,2,…,K)为用户k的发射信号矢量，令x=[xT1,…,xTK]T∈CK×1，协方差矩阵满足Rx=ε[xxH]=IK,ε[·]表示期望值。发射端的预编 码 矩 阵 为 B=diag(b1,b2,…,bns)∈ Cns×ns，若Ps为发射端的最大发射功率，则发射端满足Tr(BxxHBH)=Tr(BBH)≤Ps的发射功率约束，Tr(·)表示矩阵的迹。中继接收信号为

式中：H=[H1,H2,…,Hns]T∈ Cnr×ns为每个用户到中继节点对应的等效信道矩阵，nr是方差为的中继端接收噪声。

第二个时隙，中继端将预编码后的信号转发至接收端，中继转发信号yr∈Cnr×1为

式中：F ∈ Cnr×nr为中继节点处预编码矩阵；yr满足中继功率约束条件Tr(yr)≤Pr，Pr为最大转发功率。接收端信号yd∈Cnd×1可以表示为

式中：G ∈ Cnd×nr为中继到接收端的信道矩阵，n∈Cnd×1是协方差矩阵为R= ε[n]=I的接收dnddnd端噪声。接收端采用线性处理矩阵Q对其接收信号进行恢复，最终恢复出发送信号的估计值可表示为

2 信道模型

由于信道估计方法的局限性和信道反馈链路的时延性客观存在，实际的MIMO中继通信系统中无法获得理想信道状态信息。本文考虑信道信息存在估计误差，且信道信息反馈存在延迟情况。假设Hˉt为时刻t接收端对真实信道矩阵Ht的估计信道矩阵，则Ht为[11]

式 中 ：Eh∈ Cnr×ns为 Ht的 估 计 误 差 矩 阵 ，其 元 素 服 从 ei,j～CN(0,)；的 元 素 服 从～CN(0,1-)；CN(0,σ2)表示均值为 0，方差为 σ2的复高斯分布。为接收端经过时延为 τh的反馈链路反馈至发射端的信道估计矩阵，则信道估计矩阵及反馈延迟信道估计矩阵的关系如下[12]

根据 Clarke功率谱，ρh为与时延有关的时间相关系数，ρh=(2πfdτh)[13]。fdτh为归一化反馈延迟，J0代表第一类零阶Bessel函数。Dh为元素满足dij～CN(0,(1-)(1-ρh))的反馈延迟估计误差矩阵。由式(5，6)可得，反馈延迟信道估计矩阵Hˉt-τ与真实信道矩阵Ht存在如下关系[14]

由于Eh与Dh相互独立，令Σh=Eh+Dh，式(7)可以表示为

注意，式(8)虽然与式(6)形式相类似，但误差矩阵Σh由Dh和Eh组成，其元素服从kij～CN(0,(1-)(1-ρ)+)。时刻t与时刻t-τh信道矩阵元素都服从同一复高斯分布，为推导方便将时间下标省去，因此信道矩阵最终简化为

用H和G分别表示发射端到中继和中继到接收端的真实信道矩阵，记Σh=Eh+Dh，Σg=Eg+Dg，得到

式中：H 和 G 的元素分别满足 hi,j～CN(0,1)和 gi,j～CN(0,1)，时间相关系数满足 ρh=(2πfdτh)和ρg=(2πfdτg)。Dh和Dg分别为信道矩阵H和G对应的反馈延迟误差矩阵，Eh和Eg分别为对应的估计误差矩阵，Σh的元素服从 kij～CN(0,(1-)(1-ρh)+)，ΣG的元素服从 gij～CN(0,(1-)(1-ρg)+)[15]。

3 基于MMSE的约束优化问题

根据最小均方误差为设计准则，均方误差函数可表示为

根据信道模型，有

式中

则均方误差函数可进一步化简为

需进行优化的目标函数为均方误差MSE(B,F,Q)，将发射端与中继节点处的功率作为约束，因此优化问题可表示为

4 上行多用户MIMO中继系统的预编码设计

本文将预编码算法采用适当的矩阵变换，将式(18)中求解发射端，中继端，接收端矩阵的复杂非凸问题分解为3个独立的子优化问题，分别对其求解后采用联合迭代法进行优化。

4.1 发射端预编码矩阵设计

发射端的用户服从独立空间分布，则发射端矩阵B需满足为对角矩阵，且满足功率约束条件：Tr(BxxHBH)=Tr(BBH)≤Ps。假设每个用户配置其最大功率，则

即可得到[16]

式中Ps为diag(P1,…,Pns)的对角阵。

4.2 中继端预编码矩阵设计

固定B和Q，可将优化问题式(18)转化为SDP半正定规划问题以求解F[17]。由式(18)，该子问题可表述为

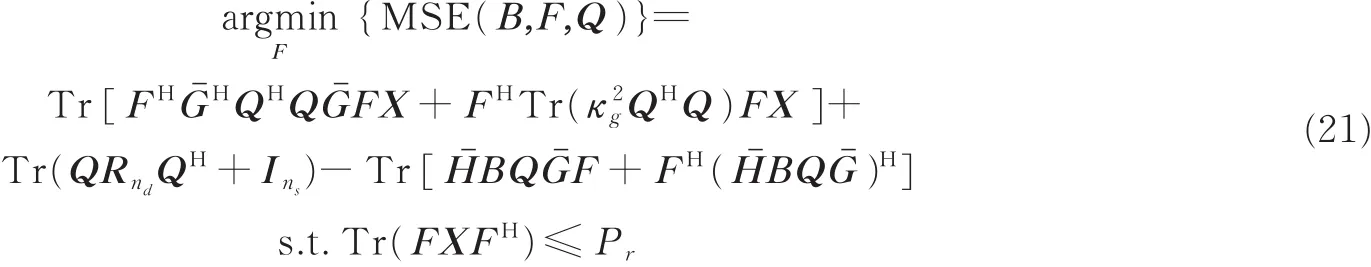
式(21)的优化问题为含有单一约束条件的SDP问题。由数学性质Tr(AHB)=vecT(A)vec(B)与vec(AXB)=(BH⊗ A)vec(X)，有

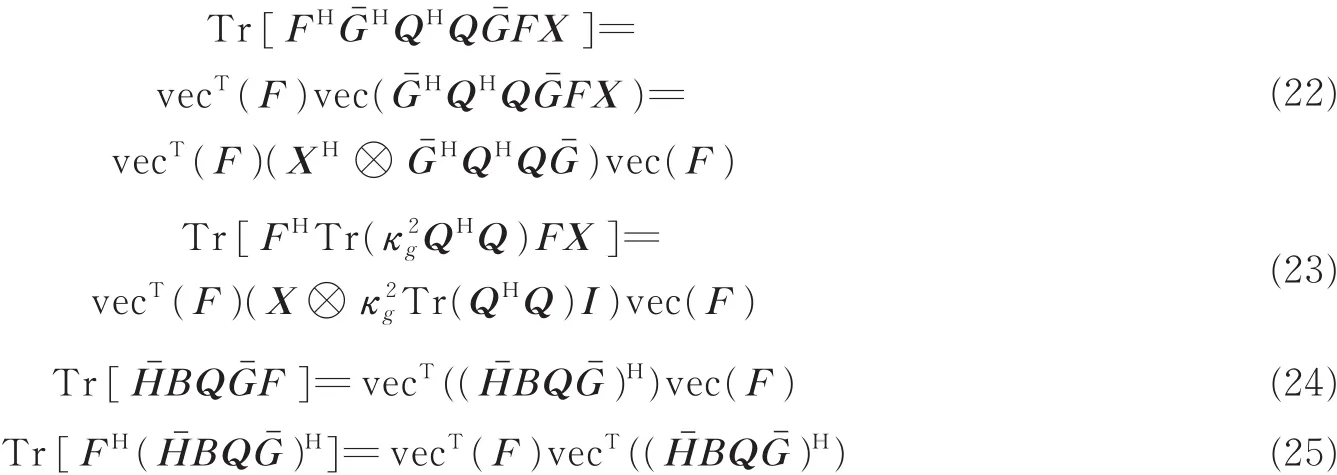
式(21)中的子问题可采用如下转化

式(26)中对应参数为

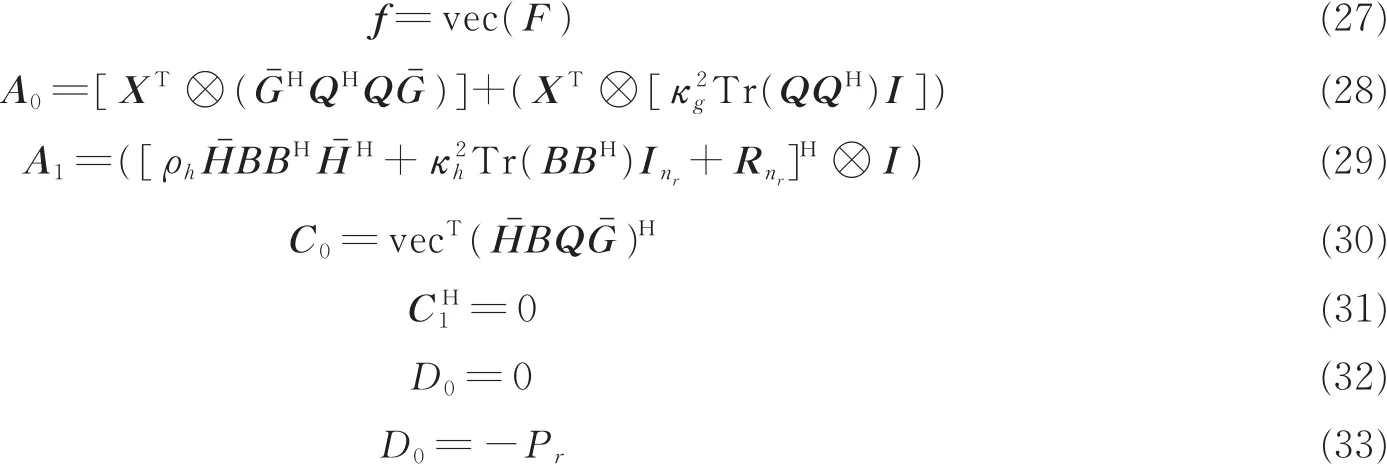
当引入对应变量χ后，式(26)可以转化为如下SDP问题

对式(34)的SDP问题采用CVX工具箱求解[18]，可得到中继预编码矩阵F。

4.3 接收端处理矩阵设计

这里采用线性搜索法求解接收端处理矩阵Q[16]。在此之前，需要先求得F。由中继功率约束条件，求解F的子问题可以表示为

引入拉格朗日乘子λ后，式(35)的拉格朗日函数可表示为

由KKT条件有

联立式(37—40)，可得F表达式为

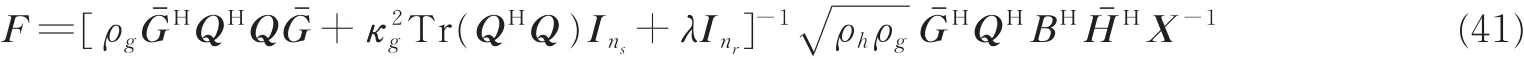
由文献[16]，引入线性系数η(η＞ 0)，用η-1Q代替Q，则F可表示为

ϖ被定义为

将式(42)代入式(17)，可得

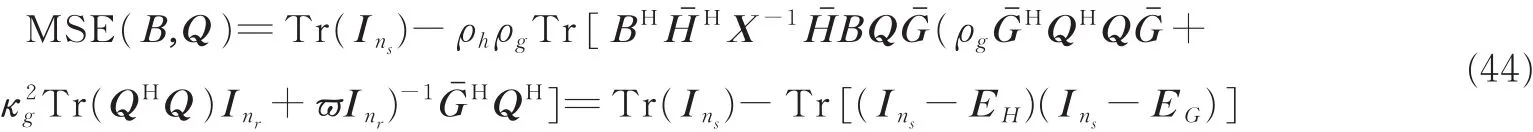
式中

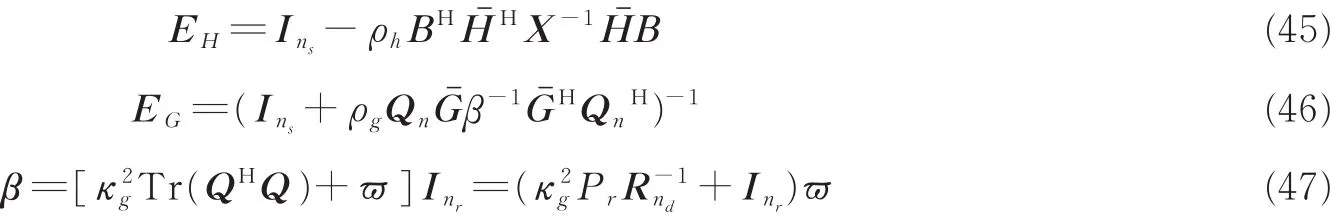
借助线性搜索法求解该无约束最优化问题[16]

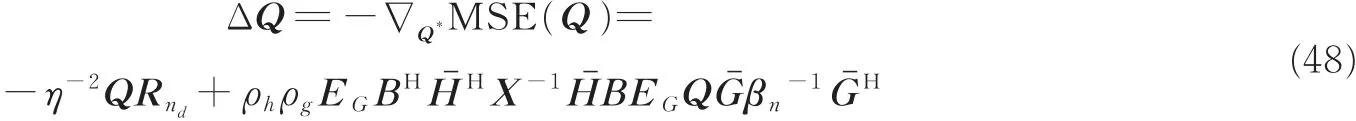
线性搜索法的求解步骤如表1所示。

4.4 联合迭代算法

以上可以看到发射端矩阵B，中继转发矩阵F，接收端处理矩阵Q相互关联，下面采用联合迭代设计算法，迭代更新求得 Bopt，Fopt，Qopt，如表 2 所示。

由联合迭代法的设计步骤，其收敛性需由以下两点保证：

表1 线性搜索法Tab.1 Linear searching method

表2 上行多用户MIMO中继系统联合迭代算法Tab.2 Jointiterative algorithm ofup-link multi-users MIMO relay system

(1)MSE(B(n),F(n),Q(n),β(n),η(n))为收敛序列。

(2)B(n),F(n)和 Q(n)收敛。

经过i次迭代，得到MSE(B(i),F(i),β(i),η(i))，假定第i+1次迭代时有：当F(i)固定时，满足

即在第i+1次迭代中，B(i+1)为极值点。此外，均方误差值的下界为零，因此该极值点为极小值点，所以MSE(B(i+1),F(i),β(i),η(i))≤ MSE(B(i),F(i),Q(i),β(i),η(i))，因此 MSE(B(i),F(i),Q(i),β(i),η(i))为单调递减的收敛序列，F(i)收敛。同理，可证B(i)和Q(i)收敛。以上保证了该迭代算法的收敛性。另外，η的引入是为了方便预编码矩阵的求解，对算法的收敛性以及系统的均方误差和误比特率性能均无影响。

5 仿真结果与分析

本节给出不同CSI下本文预编码方案的比特误比特率仿真结果，并将该联合迭代方法与放大转发方案(即Ind)进行性能对比[19]。仿真中，假设两个时隙内的信道都是瑞利平坦衰落信道(两时隙内信道状态不变)，发射端对信号采用QPSK调制。发射端、中继节点及接收端的天线数ns=nr=nd=4；中继节点和接收端加性复高斯噪声的方差分别为和；发射端到中继端的信噪比为SNRsr=Ps/(ns)，中继端到接收端的信噪比SNRrd=Pr/(nr)。信道参数定义为：归一化反馈延迟fdτ=fdτh=fdτg；信道估计误差==。最大迭代次数Niter=30，迭代门限值ξ=0.001。

图2,3为固定信噪比SNRsr=25 dB时采用所提预编码算法的误比特率性能曲线。图2为fdτ设置了对比，两组对比参数分别为fdτ=0.01,=0.02和fdτ=0.03,=0.02。图3为设置了对比，两组对比的参数分别为fdτ=0.01=0.01和fdτ=0.01,=0.03。

图2 =0.02时上行多用户MIMO中继系统误比特率比较(SNRsr=25 dB)Fig.2BER performance comparisons with=0.02(SNRsr=25 dB)

图3 fdτ=0.01时上行多用户MIMO中继系统的误比特率比较(SNRsr=25 dB)Fig.3 BER performance comparisons with fdτ=0.01(SNRsr=25 dB)

当固定上行信道信噪比SNRsr=25 dB时，系统比特误比特率性能随下行信道信噪比SNRrd的影响如4和图5所示。图4中参数分别设置为fdτ=0.01,=0.02和fdτ=0.03,=0.02。图5中两组对比的参数：fdτ=0.01,=0.01;fdτ=0.01,=0.03。

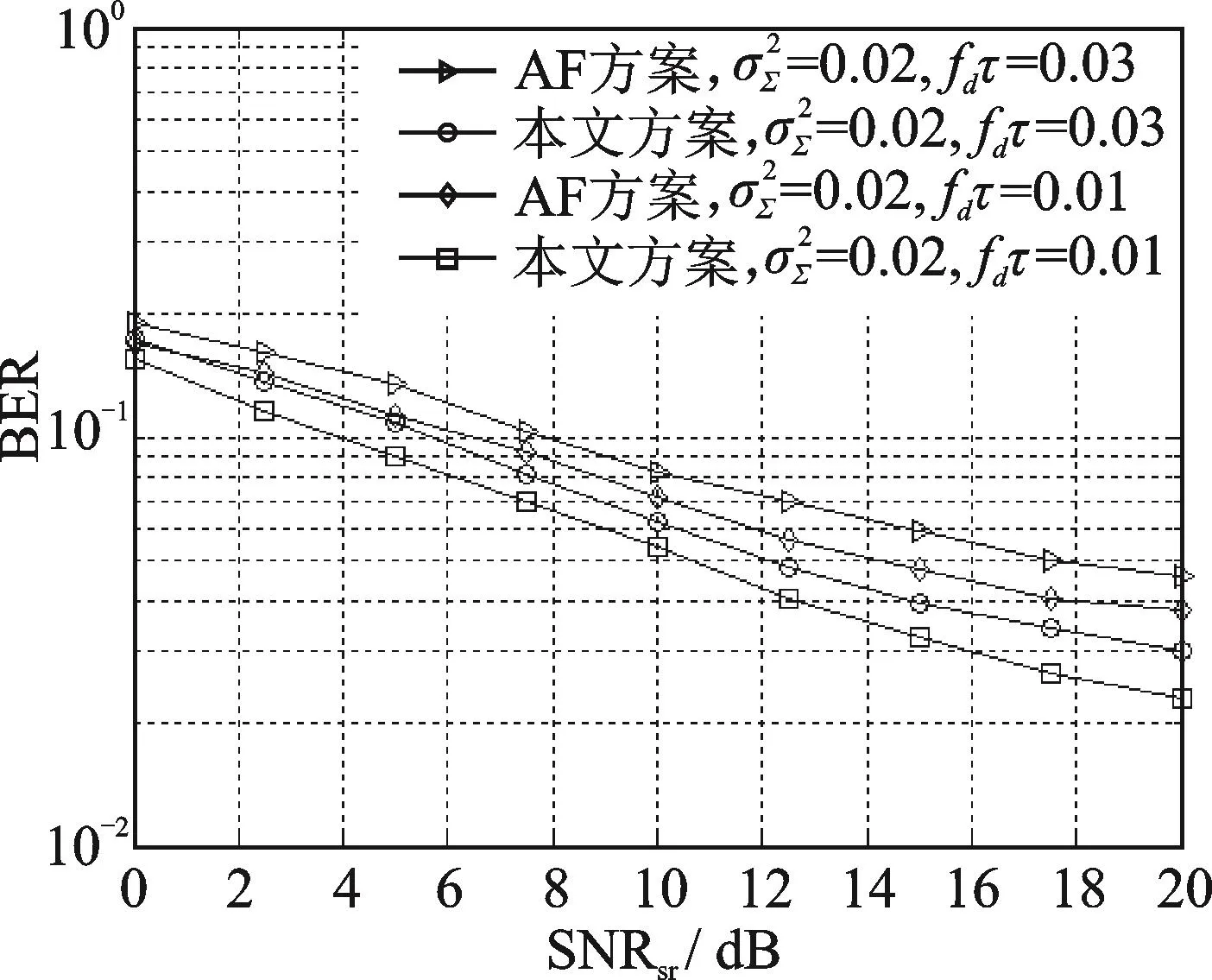
图4 =0.02时上行多用户MIMO中继系统误比特率比较(SNRrd=25 dB)Fig.4BER performance comparisons with=0.02(SNRrd=25 dB)

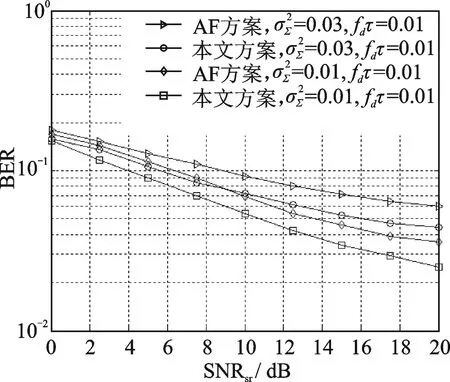
图5 fdτ=0.01时多用户MIMO中继系统的误比特率比较(SNRrd=25 dB)Fig.5 BER performance comparisons with fdτ=0.01(SNRrd=25 dB)

由图2—5可以看到随着fdτ和σ2Σ增大，系统BER逐渐减小，这是信道传输质量变差所致。此外，本文预编码方案的系统性能明显好于对比的AF中继方案。在高SNR域，随着信道估计误差和信道反馈延迟的增大，性能优势也越来越明显。这是由于AF方案仅考虑发射端与接收端的线性处理，未在中继对信号进行预编码，仅对信号做了放大转发处理，而所提预编码算法不仅综合考虑了信道估计误差及反馈延迟对中继收发信号的影响，还对各节点进行了联合设计，因此性能要比中继处未进行预编码的AF中继方案表现优异。

图6和图7为系统在不完全CSI条件下，本文方案与仅考虑部分信道信息方案的性能对比图。以信噪比SNR=SNRsr=SNRrd作为横轴，对比的性能为系统误比特率。图6固定一类信道参数fdτ，以估计误差为对比，图6的信道参数设置为fdτ=0.01,=0.02和fdτ=0.03,=0.02。图7则以归一化反馈延迟fdτ为对比，信道参数设置为fdτ=0.01,=0.01,fdτ=0.01,=0.03。

图6 以fdτ作为参照的本文方案与仅考虑部分CSI方案的误比特率比较(SNRsr=SNRrd)Fig.6 BER performance comparisons withfdτas reference and considering partial CSI(SNRsr=SNRrd)

图7 以作为参照的本文方案与仅考虑部分CSI方案的误比特率比较(SNRsr=SNRrd)Fig.7BER performance comparisons withas reference and considering partial CSI(SNRsr=SNRrd)

从图6和图7的仿真结果可以看到，无论采用哪组仿真参数，本文预编码方案的系统性能表现都最优异。这是由于所提方案充分考虑有限反馈系统中的量化信道模型和信道估计时的误差，因此相比仅考虑了部分信道信息的对比方案表现要好。

6 结束语

针对不完全信道状态信息的多用户MIMO中继系统，本文提出了基于MMSE准则的预编码设计方案。选用发射端配备多用户的上行多用户模型，采用适当矩阵变换，将发射端，中继节点，接收端矩阵求解的复杂非凸问题分解为3个独立的子优化问题。发射端服从独立分布可先确定发射端预编矩阵，将中继矩阵求解的凸优化问题转化为SDP半正定规划问题，可以利用CVX工具箱求解。接收端处理矩阵可通过引入修正因子的线性搜索法求解。最后采用联合迭代法得到各节点矩阵的最优解。系统性能仿真结果表明，与对比方案相比，所提预编码算法能获得更优的系统性能。与仅考虑部分CSI的方案相比，所提预编码算法能获得更低的误比特率。