基于三轴磁通门传感器的随钻方位伽马测量系统设计
2019-04-25吕海川陶海君熊祖根
吕海川, 陶海君, 熊祖根
(1中国石油集团工程技术研究院 2中国石油集团川庆钻探工程有限公司长庆钻井总公司 3中国石油集团川庆钻探工程有限公司钻采工程技术研究院)
LWD工具所测数据中,最常用的是伽马数据由连续的伽马数据形成的伽马曲线是区分地层边界的最佳选择[1],其他的LWD数据曲线(如电阻率、密度、中子等)都要结合伽马曲线来确定分层,然后做数据分析[2]。自然伽马工具测量的是测点位置井眼各方向地层的平均伽马值,当钻具穿过不同地层,伽马测量数值会发生变化,虽然通过伽马曲线可以直观地显示钻具穿过的层位发生了变化,但是不能判断出是从什么方位穿过层位分界的。在储层较薄且地层存在不规则弯曲的情况下,仅靠自然伽马数据,不能给采取准确的回调措施带来更多的参考信息;不准确的回调措施存在降低储层钻遇率的风险[3]。方位伽马是对自然伽马的优化升级,给测量数据加上方位信息,即按照重力方向把测点的圆周等分为4、8或者16扇区,硬件测量和软件计算相结合,测出每个扇区的伽马数据。通过实时的上、下扇区伽马数据曲线,在钻具偏离储层时,可以分析出钻具偏离储层的方向,这样就可以采取正确的回调措施,及时正确调整钻具返回储层,减少储层钻遇率损失[4]。通常,划分扇区依据的标准是重力工具面,在硬件上使用沿探管径向和轴向分布的三轴正交重力加速度计,经过软件计算出某个时刻的重力工具面并对应到相应的扇区。重力加速度计对震动和离心力都比较敏感,钻井作业时的震动以及复合钻进时的旋转,都会对重力加速度计测量结果产生较大的影响,降低重力工具面的计算精度。在井斜和方位变化不大的情况下,重力工具面和磁性工具面之间角差相对固定,而磁通门不受震动和离心力影响,使用磁通门替代重力加速度测量和计算扇区,可以在随钻作业过程中,测量出准确的扇区位置。使用三轴磁通门代替两轴磁通门的优点是可以检验磁通门传感器是否处于正常工作状态,确保测量数据正确。应用三轴磁通门技术设计扇区测量系统的方位伽马工具,可以在震动较强、复合钻进等工况状态下提供准确的方位伽马数据,为地质导向作业提供有效的方位数据,可优化井眼轨迹,提高储层钻遇率。
一、基本原理
方位伽马测量系统,是在自然伽马的基础上,把井壁等分为若干扇区,实时计量出各个扇区内的伽马数据[5]。自然伽马数据通常由NaI晶体和光电倍增管构成的闪烁计数器来测量,地层各方向的伽马射线都可以进入晶体形成计数,所以自然伽马测量的是井眼平均伽马。方位伽马工具需要对晶体屏蔽,只留一定大小的窗口,只有窗口所在位置地层的伽马射线进入到晶体中,经过光电倍增管形成计数,其他位置的伽马射线不能穿透屏蔽层。这种带有检测窗口和屏蔽结构的伽马传感器,称为聚焦伽马传感器。
通过旋转聚焦伽马传感器,就可以实现对井眼圆周位置不同方向的伽马射线按照划分的扇区进行测量。聚焦伽马传感器不具备识别方向的功能,需要与扇区检测模块相配合,实现方位伽马计数。通常测量位置按照重力工具面所在圆周可划分为4、8或者16个扇区。扇区检测模块用来检测当前开窗位置所在的扇区,通过计数软件模块,把每个扇区的伽马计数准确地归入到对应扇区计数数组项中,这样得到方位伽马数据。在实际的作业中,受泥浆脉冲器传输速率的限制,往往会实时上传4扇区数据,重点分析上下扇区伽马曲线;在井下工具中存储8或者16扇区数据,用来做地层成像数据处理。
扇区是根据重力工具面角来划分,高边为上,低边为下。计算重力工具面常用的传感器是重力加速度计,通过安装在探管径向相互垂直的X、Y重力加速度计来测量和计算重力工具面,再由重力工具面算出当前扇区。在实际的作业中,重力加速度计很容易受到钻具震动和旋转离心力的影响,严重降低计算精度。利用磁性工具面与重力工具面在井斜和方位角相对稳定的区域内角差相对固定的特点,使用磁通门代替重力加速度计计算工具面。用两个安装在仪器径向的互相垂直的两个磁通门X和Y,在仪器静态时,采集磁通量,计算出磁性工具面,同时采集并计算出在该位置下的重力工具面,算出两者之间的角差。磁通门受到震动和旋转的影响很小,在工具钻进的过程中,实时测量磁性工具面,根据角差计算出重力工具面,获得当前伽马探管的开窗位置,由此得到窗口所在扇区,为伽马计数模块提供较准确的扇区信息。
重力工具面角GTF与磁工具面角MTF之间的角差GM是地磁在钻具横截面上的投影与高边的夹角,只与井斜角α和方位角β有关,与钻具转动角度(即GTF自身)无关,如图1所示。而磁工具面角MTF可由两轴磁通门(X轴、Y轴)的测量值直接解算而得出,且磁通门的测量精度几乎不受震动冲击和旋转工况的影响。所以,在连续旋转条件下,对重力工具面角的实时测量,可转化为对磁工具面角的实时测量,然后再利用两者间的角差GM进行补偿。

图1 重力工具面与磁性工具面关系图
二、系统设计
整个方位伽马测量系统由硬件和软件两大子系统组成,硬件子系统实现扇区检测和伽马测量,软件子系统实现以扇区为单位的伽马计数。从系统功能的角度来划分,分为扇区检测模块和伽马计数模块更为合理,前者实现扇区测量,软件与硬件相结合,后者实现针对扇区的伽马计数,主要以软件算法为主。
1. 扇区测量模块设计
扇区测量模块的功能是给伽马计数模块提供准确的扇区指示,并计算实时转速。扇区测量模块要求在静态状态下,精度达到±0.2°;旋转状态下,精度达到±2°。在滑动钻进和复合钻进过程中,扇区测量精度不小于±2°。
扇区测量模块由两个子系统组成:硬件子系统和软件子系统。其中硬件子系统由三轴磁通门及与之配套的激励电路、AD采样电路组成;软件子系统实现测量控制和数据计算,并对外输出扇区指示。
1.1 传感器选型
使用磁通门替代重力加速度计实现扇区测量。根据功能和性能要求,选择TRI-MAG-210C型三轴磁通门作为扇区测量模块用的磁传感器,该磁通门的主要技术指标见表1。
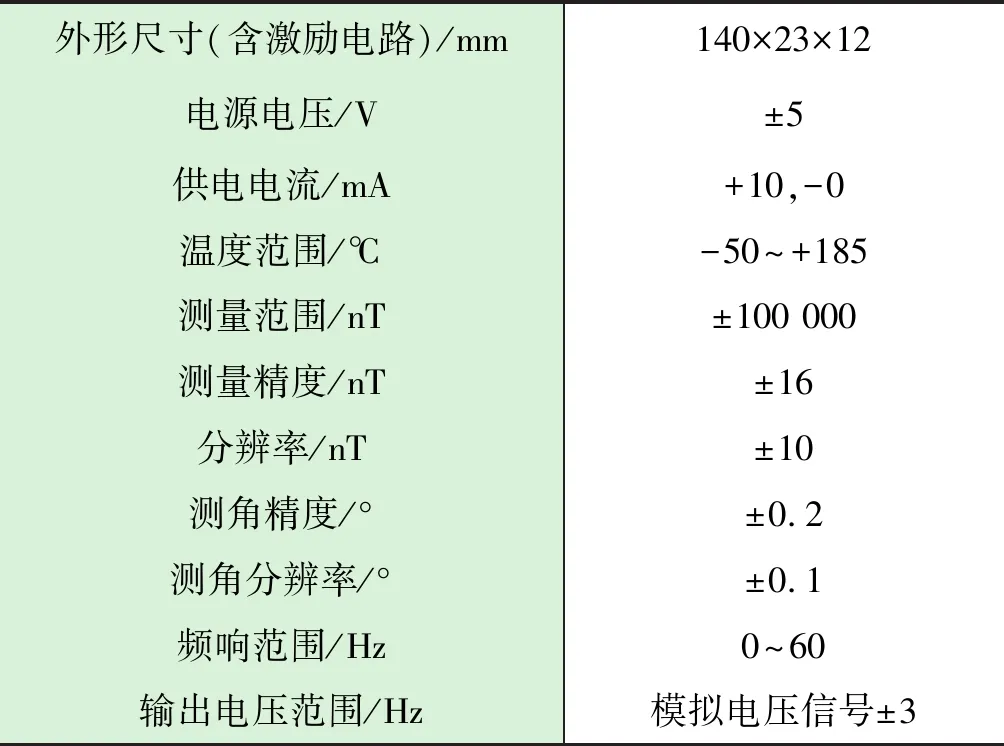
表1 TRI-MAG-210C技术指标
选用其中的X轴和Y轴作为检测轴,Z轴辅助检测和确认磁通门工作状态正常,确认测量数据不超标。
1.2 扇区测量模块结构设计
磁通门模块需要外部提供+5VDC和-5VDC供电,内置激励电路,输出三轴模拟电压信号,信号范围[-3 V,+3 V]。为提高采样精度,使用独立的AD采样模块,选择ADS1220系列AD转换芯片,该芯片高精度、低功耗,支持24 bit高精度模数转换。
为提高测量响应速度,使用独立的MCU管理扇区测量模块。扇区测量模块与MWD和伽马计数模块之间通过485数据总线通讯,扇区测量模块与伽马计数模块之间通过特定的IO管脚实现扇区指示。
整套系统使用统一的电源供电,电源电压20VDC。电源进入扇测模块后,通过一个专用设计的电源模块,转换为±5 V电源输出,给三轴磁通门供电。
采用485数据总线连接各个模块,实现数据通讯。485总线具有稳定可靠、可挂接多个子节点的有点,适用于工业产品应用。系统结构图见图2。
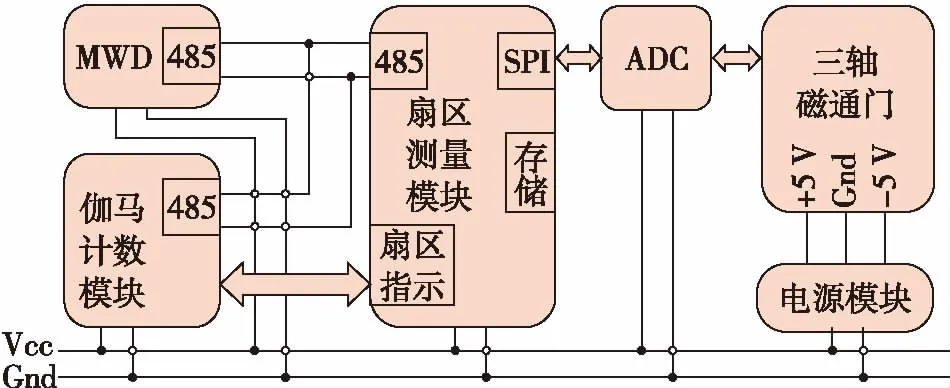
图2 扇区测量模块结构示意图
1.3 扇区测量算法
扇区测量模块的主要功能是向伽马计数模块提供扇区指示,同时,在静态时响应来自上位机的工具面查询请求。扇区测量算法的流程如图3。

图3 扇区测量算法流程图
准确地计算出磁性工具面和重力工具面之间的角差,是保证扇区计量结果准确的基础。必须在仪器处于静态的时候,测量出这两个工具面,计算出角差。为提高测量数据的精度,可使用MWD测斜仪测量结果作为计算参考量。
扇区测量模块中,计算扇区是优先级最高事件,一旦测量定时到时,要优先计算出当前位置的扇区数据,在伽马开窗跨越扇区时及时给出扇区指示。低优先级事件可以在扇区定时到时之前去响应。
为降低系统符合,还可以对扇区测量算法进行优化,加入一定的预测机制。根据前一圈的转速,预测本圈每个扇区的到达时间。
2. 伽马计数模块设计
方位伽马计数模块设计的重点在伽马计数和扇区对应两个方面。要求准确、稳定、能够动态反映出伽马的变化,为地质导向控制提供可靠的参考数据。
2.1 伽马计数算法设计
伽马射线具有放射性涨落[6],在相等的时间间隔内做重复测量,每次记录的数值是不同的。放射性涨落是微观世界的客观现象,与测量条件无关。如果按照实时测量值来上传,就会得到波动性很大的数据,无法以此为依据来判断岩性。为降低波动性,需要增加测量时间,在一定的测量时间内,伽马测量结果会相对稳定。较直接的伽马计数算法是设定一个计数周期T,在计数周期内,累计伽马计数n,计数期满之后,把计数结果n转换成对应的API值[7],作为测量结果;同时启动下一轮计数。这种方法的优点是简单、稳定、易于实现,只要T设置恰当,伽马测量结果就会保持相对稳定。不足在一轮计数中期内,上报给上位机的结果都是一样的,T值较大的话,有可能漏掉地层细节。
改进的算法是,把T再细分为更小的时间间隔t,每隔时间t完成一个计数项并保存,再启动下一个t时间计数。当上位机需要伽马数据时,从最近的一个已经完成的计数项开始,逆向累加各个计数项的时间和伽马计数,直到累加时间≥T,把伽马计数结果n转换成对应的API值。这样的算法改进,不仅保持了伽马测量稳定的优点,同时又使伽马测量具备实时性,尤其是在地层变化时,能够精细地反映出地层变化的细节。在算法实现上,要求在内存中开辟至少(int)[(T+t-1)/t]+1个数据项,用来记录每个t周期的测量数据。
2.2 扇区计数算法设计
扇区计数算法,是在伽马计数算法的基础上,为每个数据项增加了方位信息,即扇区信息。每个数据项由三个基本元素组成:计数时间、伽马计数和扇区。每完成一个数据项的条件为:计数时间到达周期t,或者仪器旋转到下一个扇区。当上位机要某个扇区的伽马测量值时,从最近的已经完成的计数项开始逆向查找,对比扇区号与当前要查找的扇区一致,然后累加时间和伽马计数值,当计数时间累加够T时,用伽马计数累加和换算出API值返回。这个算法的优点是数据稳定性好,同时兼顾了实时性;不足之处在于内存占用较大。假设划分为8个扇区,则在理想匀速旋转的状态下,每转一圈需要时间t,则至少(int)[(T+t-1)/t]×8+1个数据项。如果转速提高,一圈的时间小于t,则需要按比例增加数据项。在实测中记录到,复合钻进中,近钻头位置的转速会达到240 r/min以上,在这种情况下,每个扇区的时间只有30 ms。假设T为30 s,至少要8 000个以上的数据项,对内存要求很高。
上述的算法虽然易于实现,但是内存占用高,能够满足应用的单片机的选择范围会大大缩小。对算法做适当改进,在保证性能的基础上,降低内存占用。把每个数据项的元素改为:计数时间、伽马计数数组[8],其中伽马计数数组分别对应1~8个扇区。计数时间片依然使用t,在时间片t内,按照扇区模块的指示,把伽马计数写到对应的数组项中;时间满t,本数据项计数完成,开始使用下一个数据项计数。这个算法,虽然增加了实现的复杂度,但是解决了数据项数与转速的关联关系,数据项数不再受到转速影响,有效地降低系统对内存容量的要求。
2.3 伽马刻度方法
因为方位伽马对自然伽马探管做了屏蔽处理,需要对方位伽马仪器做刻度,得到准确的刻度系数k;同时,为确保数据统一,把计数转换到API标准中。为确保刻度系数的准确性,使用二级刻度器进行标定刻度。首先在低值刻度模块中,计数时间Tc,得到计数值N1;再放置到高值刻度模块中,计数时间Tc,得到计数值N2。高低刻度模块标称值差为A,刻度系数K=(N2-N1)/A,用这个系数完成伽马计数与API值的转换。
三、现场试验情况
2017年11月6日至11月11日,方位伽马工具在山西临汾大宁3-7向2水平井进行现场试验。钻具组合:PDC钻头+螺杆+扶正器+无磁钻铤+MWD悬挂短节+钻铤(13根)+钻杆,其中测量工具组合为居中式方位伽马+定向探管。实时上传工具面、上下左右四扇区方位伽马数据,地面软件绘制上下方位伽马曲线。
试验井段为1 980~2 491 m,总进尺511 m,循环时间198 h,排量30 L/s,钻井液密度1.1 g/cm3,黏度45~55 s。整个试验过程中,仪器工作正常。
钻进至2 122 m左右时,曲线显示下伽马数据开始增大,随后上伽马数据增大,增大之后两条曲线又稳定重叠。从伽马数据变化分析,钻具从砂岩进入泥岩,离开储层。经过观察方位伽马曲线,下伽马先变化,判断为钻具从下方穿出储层。调整钻进方向,在2 140 m时,上伽马开始变小,随后下伽马也开始降低,后两条伽马曲线稳定重叠,数据显示为进入砂岩。经过与测井数据对比,确认这一段进入到泥岩,调整后返回储层,如图4所示。
根据方位伽马曲线显示的钻具与层位变化关系,准确地采取回调措施,及时返回储层,降低钻遇率损失。实时方位伽马数据以及数据变化趋势,与测井数据吻合,仪器工作正常,数据可靠。

图4 方位伽马曲线
2018年5月25日至6月1日,方位伽马工具在四川德阳中江江沙203-7HF井进行实钻试验,该井为水平井,设计井深3 126.05 m。方位伽马工具入井井深2 461 m,钻具组合:Ø215.9 mm钻头+Ø172 mm单弯螺杆+尾扶+回压凡尔+无磁钻铤+钻杆(35柱)+加重钻杆(23柱)+转换接头+加重钻杆(16柱)+钻杆,测量工具组合为居中式方位伽马+定向探管。实时上传工具面、上下左右四扇区方位伽马数据,地面软件绘制上下方位伽马曲线。
试验井段为2 461~3 095 m(提前完钻),总进尺634 m,循环时间108 h,排量30 L/s,钻井液密度1.85 g/cm3,黏度45~55 s。整个试验过程中,仪器工作正常。
钻进至3 012 m时,下伽马数据变大,疑似穿出储层,但测量的伽马数据小于泥岩内伽马值,结合工程参数的井斜角判断,分析为钻具下部接近层位边缘,于是调整钻进方向,增斜处理,大约10 m之后,整个钻具返回到储层。对伽马数据做定量分析,确认当时并未进入泥岩,而是接近储层边缘。由于调整及时,未引起偏离储层,保证了钻遇率。如图5所示。
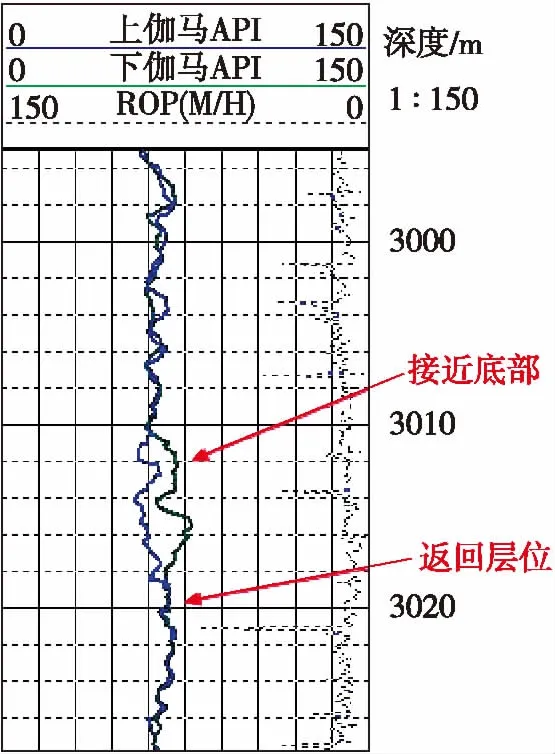
图5 方位伽马曲线
经过与测井数据对比,方位伽马测量数据与伽马测井数据一致。
四、结论
(1)方位伽马工具在自然伽马工具的基础上增加了方位信息,可分辨井眼不同方向的地层伽马数据,方位伽马数据能为提高储层钻遇率提供基础参考数据;同时存储在工具中的高密度多扇区伽马测量数据,可绘制成像伽马图,丰富地层信息,判断地层倾角,更好地服务于油气勘探开发。
(2)使用三轴磁通门代替重力加速度计进行扇区检测有理论依据,磁通门具有不受震动和旋转干扰的优势,在复合钻进的过程中实时精度测量方位伽马数据,为地质导向决策提供依据。
(3)方位伽马工具可用于居中式工具串中及近钻头短节中,在薄储层和复杂地层作业中可优化钻井轨迹,且方位伽马工具稳定可靠、操作简单、维护方便,经济性好,因此具有良好的应用前景。
