关于前缀码、极大前缀码计数问题的研究

瞿冰洁 玉溪师范学院数学与信息技术学院 指导教师 刘云

1 引言

近些年来,数字通信领域尤其是移动通信,卫星通信和计算机通信有了巨大的增长.在这些系统中,信息被表示成一个二进制的码元序列。然后这些二进制的码经过调制并被送到传输信道中传输。

因此为了确保一个可靠而高效的传输,对信息的编码需要增加各种要求和限制.这使得码的计数问题是码论中的一个重要问题,它关系到我们在实际应用中可以使用的码的数量多少,这在信息压缩、传输、纠错、加密等应用中是至关重要的。本文主要研究有限字母表上最大码字长度为任意给定值的前缀码、极大前缀码的计数问题。

2 准备知识

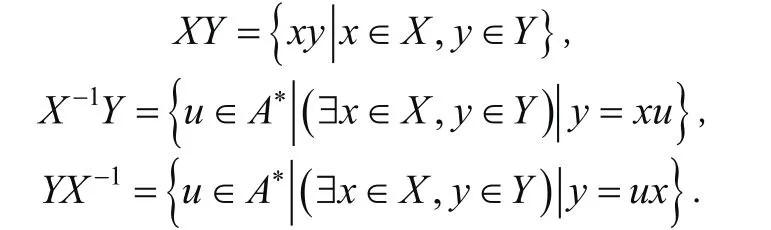
我们在本文中主要讨论前缀码的计数问题。

由定理2,3可得：

定理得证。

3 最大字长为的前缀码、极大前缀码的计数问题研究

树码022122+1=5 3252+1=26 213(此处由于码个数太多, 省略)262+1=677 6514(此处由于码个数太多, 省略)6772+1=458330 457653

从而有：

对于极大前缀,类似地有下表：

?

由定理4, 我们可得以下更一般的结论。

由定理6得：

因此最大长度为n的前缀码的个数为

同理可知：

从而有

定理得证。