巧借结论妙解题，奇思妙想三角形

江苏 韩文美

三角形的三边长与面积之间存在很多富有创意的关系.下面通过证明给出一个三角形的三边长的线性平方和与面积之间存在的不等式，并利用该不等式进一步变式拓展，得到一些相关的推论，同时利用该不等式来解决一些与之相关的最值问题.利用该不等式来处理，可使得问题的解决变得更为简单快捷.

1.结论呈现

点评：通过余弦定理加以转化，结合关系式的配凑并利用基本不等式来处理，巧妙引入三角函数的平方关系，利用柯西不等式以及三角形的面积公式来加以转化与应用，进而得以证明涉及三角形的三边长的线性平方和、三角形的面积以及相关参数之间的不等式成立.

2.拓展推论

分析：结合条件确定对应系数值x=y=z=1，结合以上不等式结论，代入即可确定三角形的三边长的平方和与面积之间存在的不等式结论.

证明：由题知x=y=z=1，

利用以上不等式结论可得

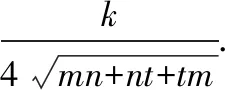
分析：结合条件确定三角形的三边长的线性平方和ma2+nb2+tc2=k为已知值，结合以上不等式结论，代入即可确定涉及三角形的面积的最大值.

证明：由于ma2+nb2+tc2=k，

分析：结合条件确定对应系数值x=a，y=b，z=c，结合以上不等式结论，代入即可确定三角形的三边长的高次代数式与面积之间存在的不等式结论.

证明：由题知x=a，y=b，z=c，

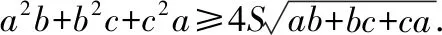
分析：结合条件确定对应系数值x=b，y=c，z=a，结合以上不等式结论，代入即可确定三角形的三边长的高次代数式与面积之间存在的不等式结论.

证明：由题知x=b，y=c，z=a，

利用以上不等式结论可得

3.实际应用

3.1三角形的三边长的线性平方和的最值问题

例1.(河南省天一大联考2018-2019学年高中毕业班阶段测试(二))在面积为2的△ABC中，a，b，c分别为内角A，B，C的对边，则a2+2b2+c2的最小值为________.

分析：结合条件确定三角形的面积值以及对应系数值x=1，y=2，z=1，结合以上不等式结论，代入即可确定涉及三角形的三边长的线性平方和的最小值.

解析：由题知S=2，x=1，y=2，z=1，

利用以上不等式结论可得

点评：利用以上不等式结论来处理此类涉及三角形的三边长的线性平方和的最值问题，解决问题易操作，目标明确，处理过程简单易懂.而采取其他相关方法来处理，过程较为繁琐，难度也比较大.

3.2三角形的面积的最值问题

例2.(2018年浙江省名校协作体试题)在△ABC中，内角A，B，C所对的边分别为a，b，c，若2a2+b2+c2=4，则△ABC面积的最大值为________.

分析：结合条件确定对应系数值x=2，y=1，z=1，结合以上不等式结论，代入即可确定涉及三角形的面积的最大值.

解析：由题知x=2，y=1，z=1，

利用以上不等式结论可得

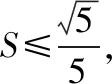
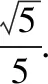
点评：利用以上不等式结论来处理此类涉及三角形的面积的最值问题，关键是结合题目条件，与以上不等式结论加以联系，这样易于操作，方便求解.而采取其他相关方法，如何将涉及三角形的三边长的线性平方和向三角形的面积转化，难度比较大，比较难破解.

3.3三角形的三边长的高次代数式的最值问题

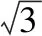
分析：结合条件确定三角形的面积值以及对应系数值x=a，y=b，z=c，结合以上不等式结论，代入即可确定涉及三角形的三边长的高次代数式的最小值.

解析：由题知x=a，y=b，z=c，

利用以上不等式结论可得

所以a3+b3+c3的最小值为24.

点评：直接来分析与求解，无法下手，又涉及三角形的三边长的高次代数式a3+b3+c3，没有较好的转化与化归思维.而利用以上不等式结论来处理此类涉及三角形的三边长的高次代数式的最值问题，巧妙地把对应的系数转化为特殊的边长问题，一般中含有特殊，可以非常有效地转化问题，进而达到解决问题的目的.

3.4三角形的三边长的其他代数式的最值问题

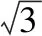
利用以上不等式结论可得

点评：破解本题是否可用其他方法来处理，大家可以尝试一下.而利用以上不等式结论来处理此类涉及三角形的三边长的其他代数式的最值问题，也是巧妙地把对应的系数转化为特殊的边长问题，此时以除法形式出现，更具一般性，而具体解答时只要加以正确转化，就可以简单快捷地处理问题，达到解决问题的目的.